- Учителю
- Образовательный минимум по математике 5, 11 класс
Образовательный минимум по математике 5, 11 класс
Обязательный минимум знаний
-
Отрезком называется часть прямой, ограниченная двумя точками;
-
Лучом называется часть прямой, ограниченная одной точкой;
-
Формулы:Единицы длины: 5. Единицы веса 6. Единицы времени
1 км = 1000 м 1 кг = 1000 гр 1 ч = 60 мин
1 м = 10 дм 1 т = 1000 кг\ 1 ч = 3600 сек
1 дм = 10 см 1 т = 10 ц 1м = 60 сек
1 см = 10 мм 1ц = 100 кг
7.Уравнением называется равенство, содержащее неизвестное число, выраженное буквой.
8. Корнем уравнения является значение неизвестного числа, превращающее уравнение в верное числовое равенство.
9. Решить уравнение значит найти все его корни или установить, что их нет.
ПРАКТИЧЕСКАЯ ЧАСТЬ
-
Решите задачу с помощью уравнения.
Андрей поймал в озере 51 рыбку. Несколько рыбок он подарил другу, после чего у него осталось 37 рыбок. Сколько рыбок Андрей подарил другу?
-
Решите уравнения : а) 63-(25+с)=26
б) (х-653)+308=417
Обязательный минимум знаний
-
Отрезком -
-
Лучом -
-
Формулы:Единицы длины: 5. Единицы веса 6. Единицы времени
__км = 1000 м 1 кг = ____гр 1 ч = __ мин
1 м = __ дм _ т = 1000 кг 1 ч = ____ сек
1 дм = __см 1 т = __ ц _м = 60 сек
_ см = 10 мм 1ц = ___кг
7.Уравнением называется
8. Корнем уравнения является
ПРАКТИЧЕСКАЯ ЧАСТЬ
-
Решите задачу с помощью уравнения.
Андрей поймал в озере 51 рыбку. Несколько рыбок он подарил другу, после чего у него осталось 37 рыбок. Сколько рыбок Андрей подарил другу?
-
Решите уравнения : а) 63-(25+с)=26
б) (х-653)+308=417
Обязательный минимум знаний
Тренировочный вариант с ответами
-
Функция F называется первообразной для функции f на
заданном промежутке, если для всех х из этого
промежутка выполняется равенство
F' х)=f(х)
Основное свойство первообразной
Теорема: Любая первообразная для функции f на промежутке I может быть записана в виде
F(х)+С, где F(х) - одна из первообразных для функции f(х) на промежутке I, а С - произвольная постоянная
Три правила нахождения первообразных
-
(F+G)= F' + G'= f+g
-
(ⱪF)' = ⱪF' = ⱪf
-
(
 F(ⱪх+b) ' =
F(ⱪх+b) ' =  F ' (ⱪх+b)*ⱪ=f (ⱪх+b)
F ' (ⱪх+b)*ⱪ=f (ⱪх+b)
Криволинейная трапеция. Формула для вычисления площади криволинейной трапеции.
1.Фигура ограниченная графиком и отрезком [a;b] и прямыми х=а, у= b называют криволинейной трапецией
2. S=F(b)-F(a)
Формула Ньютона- Лейбница.
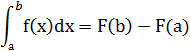
Формула для вычисления объемов тел
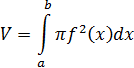
-
Практическая работа
-
Вычисли площадь фигуры, ограниченной линиями. y =
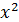 ,
y=0, x=3
,
y=0, x=3
-
Найти общий вид первообразной
а) f(x) =
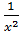
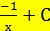 в)
f(x) =
в)
f(x) = 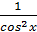 tgх+С
tgх+С
б) f(x) =
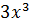
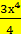 +С
+С
-
Вычисли объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями
у =
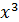 +2х ,
у=0 , х=1, х=2
+2х ,
у=0 , х=1, х=2
Обязательный минимум знаний
Тренировочный вариант без ответов
-
___________________________________равенство
F' х)=f(х)
Основное свойство первообразной
Теорема: Любая первообразная для функции f на промежутке I может быть записана в виде______
, где F(х) - одна из первообразных для функции f(х) на промежутке I, а _- произвольная постоянная
Три правила нахождения первообразных
-
(F+G)= F' + _'= ___
-
(ⱪF)' = __ = ⱪf
-
(
 F(ⱪх+b) ' = _______=f (ⱪх+b)
F(ⱪх+b) ' = _______=f (ⱪх+b)
Криволинейная трапеция. Формула для вычисления площади криволинейной трапеции.
Формула Ньютона- Лейбница.
Формула для вычисления объемов тел
-
Практическая работа
-
Вычисли площадь фигуры, ограниченной линиями. y =
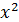 ,
y=0, x=3
,
y=0, x=3
-
Найти общий вид первообразной
а) f(x) =
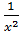
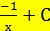 в)
f(x) =
в)
f(x) = 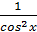 tgх+С
tgх+С
б) f(x) =
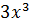
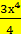 +С
+С
-
Вычисли объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями
у =
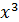 +2х ,
у=0 , х=1, х=2
+2х ,
у=0 , х=1, х=2
Обязательный минимум знанийЧетверть
1
Предмет
Геометрия
Класс
11
Тренировочный вариант с ответами
А(х1; у1;z1) и В(х2; у2; z2)
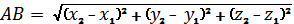
Координаты середины отрезка с концами А(х1; у1;z1);В(х2; у2; z2)
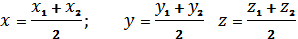
Если (х1; у1;z1) и В(х2; у2; z2), то координаты вектора
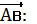
 {х2-х1;
у2-у1; z2-z1}
{х2-х1;
у2-у1; z2-z1}
Сложение и вычитание векторов
 {а1;
а2; а3;} ±
{а1;
а2; а3;} ± 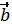 {b1;
b21; b3}
={а1±b1;;
а2±b2; а3±b3 }
{b1;
b21; b3}
={а1±b1;;
а2±b2; а3±b3 }
Умножение вектора на число
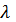
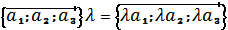
Скалярное произведение векторов
 {а1;
а2; а3;};
{а1;
а2; а3;}; 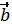 {b1;
b21; b3}
{b1;
b21; b3}
 ∙
∙
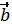 =
a1 ∙ b1+ a2
∙b2+a3∙b3
=
a1 ∙ b1+ a2
∙b2+a3∙b3
Косинус угла между векторами
 {а1;
а2; а3;};
{а1;
а2; а3;}; 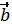 {b1;
b21; b3}
{b1;
b21; b3}

 cos(
cos( ^
^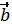 )=
)=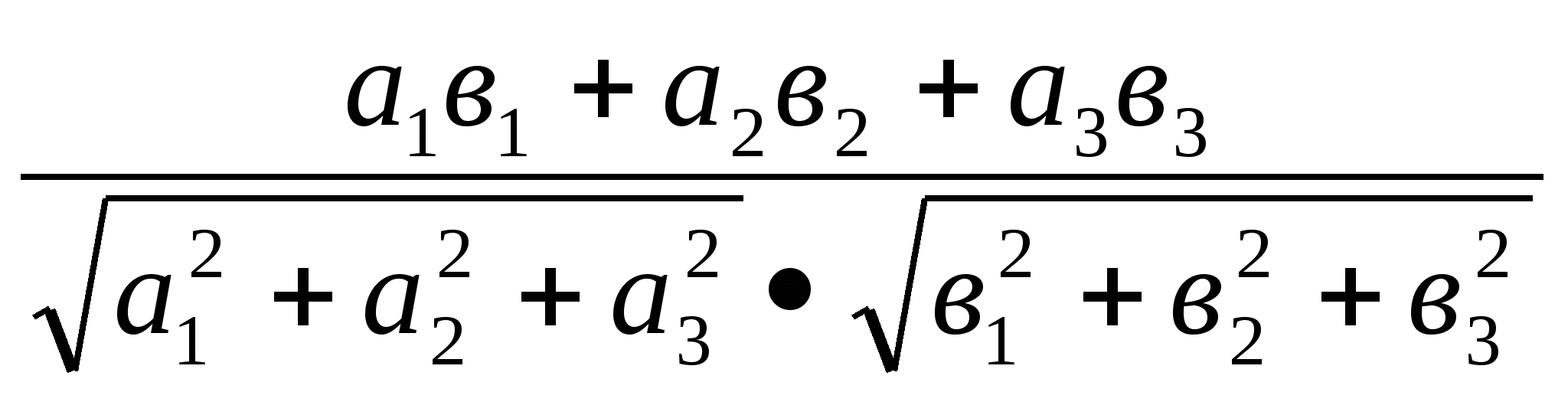
Практическая часть
-
Даны точки А(2;-4;1) и В(-2;0;3).
а). Координаты середины С отрезка АВ: С(0;-2;2 )
б). Координаты вектора
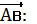
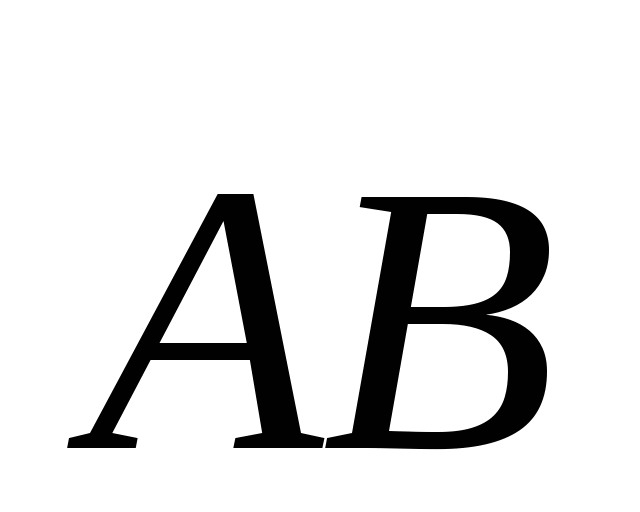
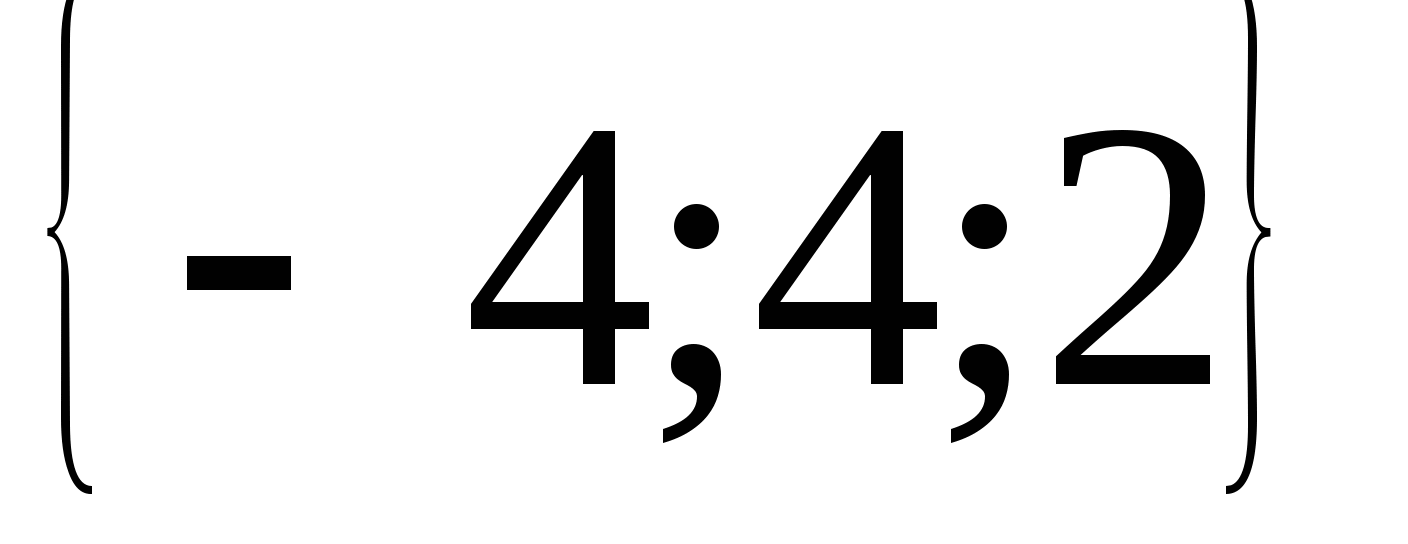
-
Даны векторы


а) Координаты вектора
 +
+
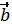
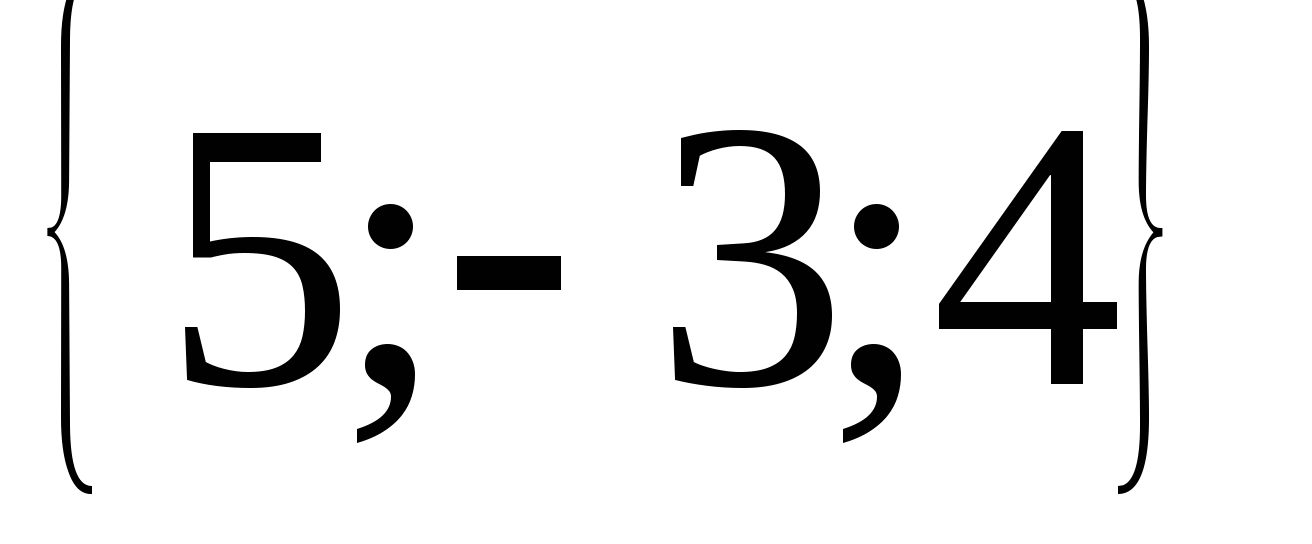
б). Координаты вектора
 -
-
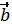
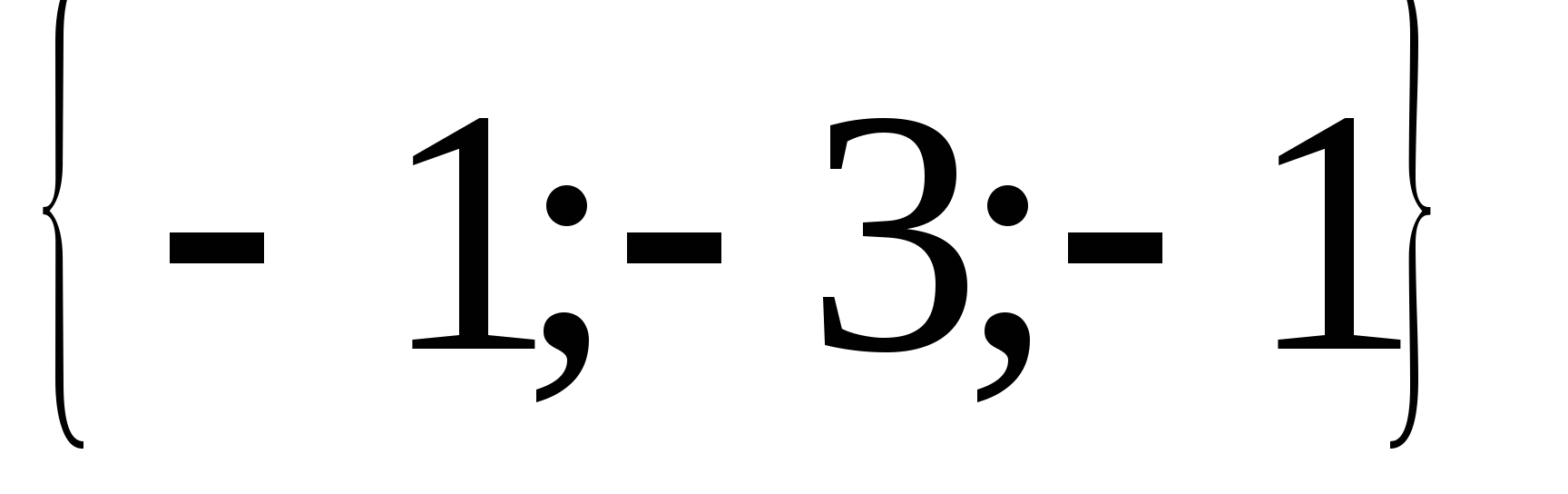
в) Координаты вектора 2
 -0,5
-0,5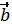
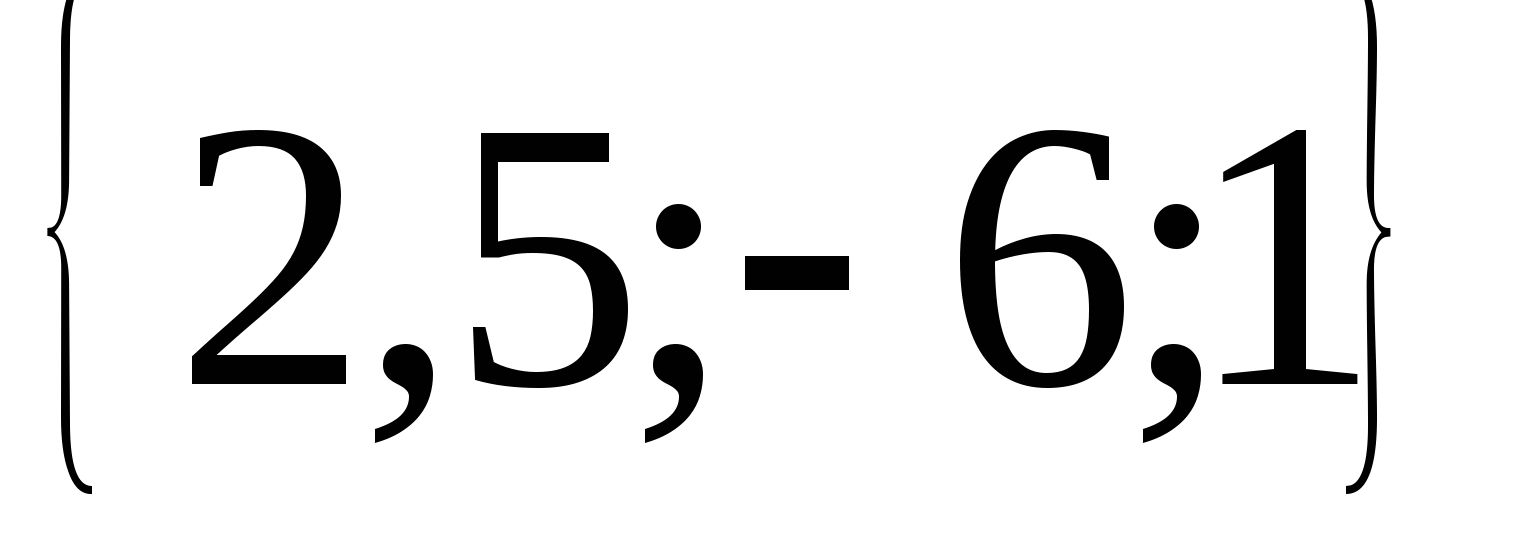
г) Скалярное произведение векторов
 *
*
 =
6+0+2=8
=
6+0+2=8
д) косинус угла между векторами cos(
 ^
^ ) =
) =
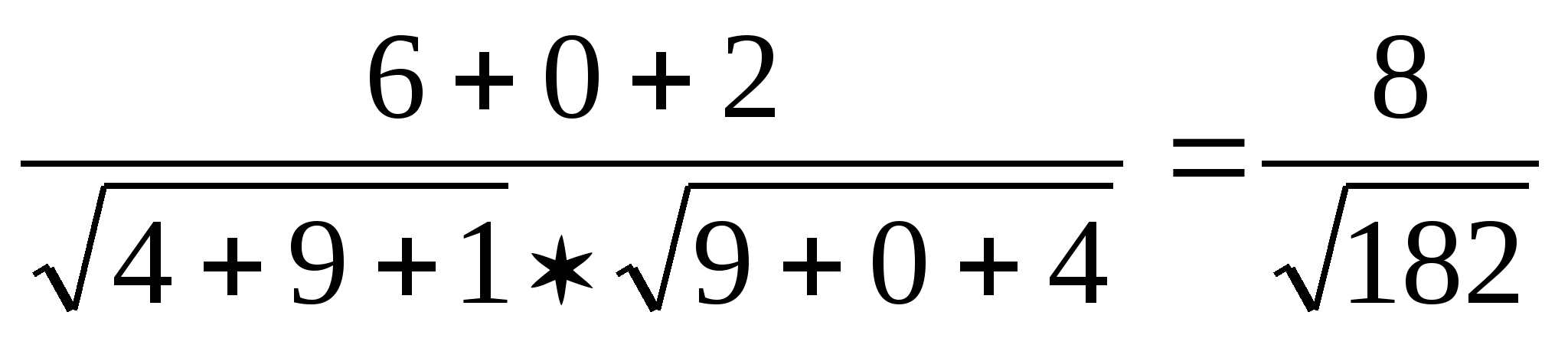 .
.
Обязательный минимум знанийЧетверть
1
Предмет
Геометрия
Класс
11
Тренировочный вариант без ответов
А(х1; у1;z1) и В(х2; у2; z2)
Координаты середины отрезка с концами А(х1; у1;z1);В(х2; у2; z2)
х=_______, у=_________, z=________.
Если (х1; у1;z1) и В(х2; у2; z2), то координаты вектора
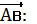
{ ;}
Сложение и вычитание векторов
 {а1;
а2; а3;} ±
{а1;
а2; а3;} ± 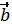 {b1;
b2; b3} ={ }
{b1;
b2; b3} ={ }
Умножение вектора на число
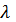

Скалярное произведение векторов
 {а1;
а2; а3;};
{а1;
а2; а3;}; 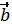 {b1;
b21; b3}
{b1;
b21; b3}
 ∙
∙
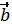 =
=
Косинус угла между векторами
 {а1;
а2; а3;};
{а1;
а2; а3;}; 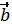 {b1;
b2; b3}
{b1;
b2; b3}
Практическая часть
-
Даны точки А(2;-4;1) и В(-2;0;3).
а). Координаты середины С отрезка АВ: С( )
б). Координаты вектора
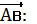
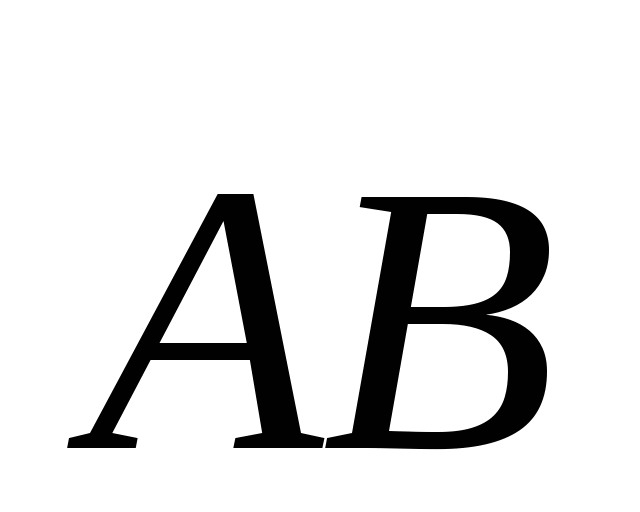
-
Даны векторы


-
Даны векторы


а) Координаты вектора
 +
+
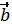
б). Координаты вектора
 -
-
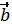
в) Координаты вектора 2
 -0,5
-0,5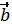
г) Скалярное произведение векторов
 *
*
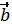 =
=
д) косинус угла между векторами cos(
 ^
^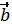 )=
)=
-
-