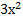
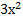
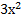
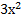
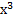
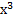
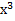
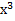
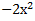
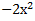
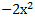
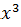
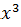
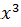
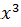
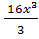
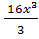
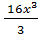
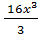
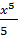
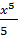
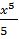
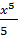
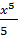
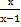
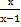
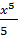
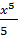
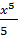
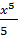
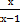
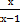
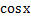
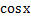
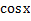
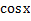
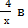
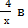
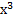
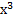
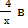
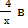
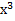
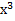
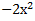
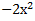
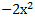
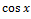
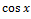
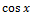
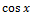
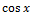
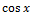
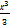
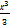
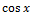
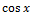
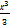
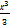
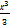
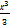
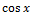
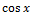
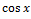
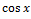
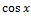
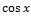
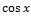
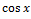
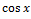
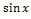
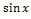
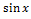
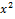
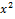
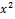
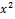
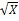
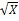
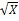
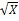
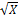
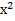
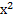
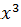
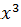
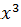
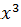
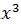
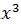
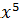
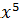
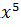
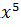
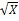
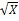
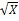
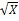
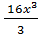
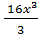
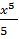
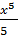
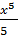
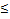
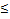
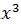
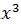
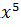
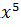
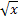
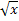
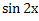
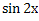
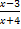
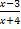
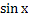
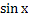
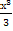
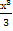
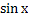
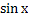
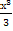
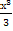
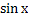
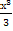
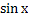
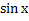
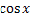
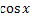
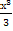
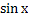
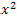
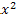
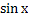
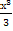
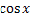
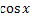
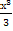
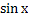
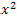
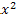
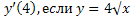
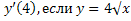
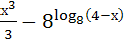
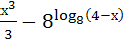
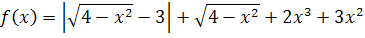
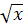
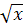
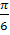
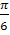
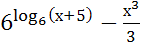
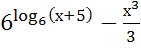
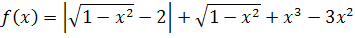
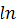
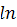
Урок обобщения и систематизации знаний в 11 классе по теме: «Производная и ее применение».

Урок обобщения и систематизации знаний в 11 классе по теме: «Производная и ее применение».

Цели урока:

Образования:

• проверить умение дифференцировать функцию и исследовать ее с помощью производной;

• установить, могут ли учащиеся раскрыть структуру и содержание понятия геометрического смысла производной;

• установить, могут ли учащиеся данный аппарат применять в различных ситуациях

Развития:

• формировать и развивать умение планировать свою работу в парах;

• формировать мыслительные навыки: сравнение, анализ, аналогия, прогнозирование.

• развивать графическую культуру учащихся.

Воспитания:

• прививать культуру общения и сотрудничества.

• формировать умения излагать свои мысли устно и письменно;

Оборудование: презентация, карточки, оценочные листы, листы для самопроверки.

Оценочный лист учащегося

Фамилия______________________________________________

Имя_________________________________________________

Этап урока

Задания

Количество баллов

1

Проверка домашнего задания

2

«Мозговой штурм»

3

Тест 1: «Заполни пропуски»

4

Тест 2: «Задачи - картинки»

5

Конкурс: «Верно - неверно»

6

Конкурс: «Выбери сам»

Итоговое

количество баллов

Оценка

Критерии оценок:

«5» - 21-25 баллов

«4» - 18- 20 баллов

«3» - 12- 17 баллов

«2» - менее 12 баллов

Ход урока:

1этап. Проверка домашнего задания (5 минут). Ученики отвечают по готовым записям. На интерактивной доске заранее заготовлено домашнее задание. Работа ведется фронтально, но пары обмениваются тетрадями и проводят взаимопроверку (слайд с домашней работой маркером на интерактивной доске).Слайд №1 -тема урока; № 2 - задачи урока.

2 этап. Мозговой штурм (слайд, №3, №4, № 5).

№ 1. Найдите производные функций:

1. У (х)=3+7-2+

2. У (х)=

3. У (х)=+2х

4. У (х)=+1

5. У (х)=

№ 2. Из скольких непрерывных «кусков» состоят графики функций:

1. У (х) = 2. У (х) =

№ 3. На рисунке изображен график функции у = f(х), заданный на отрезке

Найдите: а) точки максимума и минимума

aghf

0ghf

x₁

x₂

x₃

x₄

b

x

y

y=f(x)

б) точки, в которых функция принимает наибольшее и наименьшее значения на отрезке .

Ученикам, активно отвечающим, на вопросы устного счета учитель называет количество баллов, которые они могут поставить в оценочный лист.

3 этап. Тест №1 « Заполни пропуски».

(Заполните пропуски (многоточия), чтобы получилось верное утверждение или правильная формулировка определения или правила). Ученики работают самостоятельно, по вариантам, затем пары обмениваются вариантами и проводят взаимопроверку, сравнивая ответы с ответами на экране. За каждый правильный ответ ставится один балл.

Вариант 1. Фамилия, Имя____________________________

1. График четной функции симметричен относительно…

2. Функция возрастает на некотором промежутке, если f… во всех внутренних точках промежутка.

3. Точка х₀ называется точкой максимума функции f(х), если для всех х х₀ из некоторой окрестности точки х₀ выполняется неравенство f…

4. Условие =0 является … условием экстремума дифференцируемой функции f(х).

5. Геометрический смысл производной заключается в том, что значение производной функции в точке равно… к графику функции в данной точке.

Вариант 2. Фамилия, Имя____________________________

1. График нечетной функции симметричен относительно…

2. Функция убывает на некотором промежутке, если f… во всех внутренних точках промежутка.

3. Точка х₀ называется точкой минимума функции f(х), если для всех х х₀ из некоторой окрестности точки х₀ выполняется неравенство f…

4. Для того чтобы точка х₀ была точкой экстремума функции f(х), необходимо, чтобы эта точка была… для данной функции.

5. Пусть функция f(х) определена в некоторой окрестности х₀ и дифференцируема в этой точке. Если х₀ - точка экстремума функции f(х), то …

Тест №1 « Заполни пропуски» (слайд №6, №7)

Вариант 1

1. График четной функции симметричен относительно оси ординат.

2. Функция возрастает на некотором промежутке, если fво всех внутренних точках промежутка.

3. Точка х₀ называется точкой максимума функции f(х), если для всех х х₀ из некоторой окрестности точки х₀ выполняется неравенство f f(х₀)

4. Условие =0 является необходимым условием экстремума дифференцируемой функции f(х).

5. Геометрический смысл производной заключается в том, что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в данной точке.

Вариант 2

1.График нечетной функции симметричен относительно начала координат.

2. Функция убывает на некотором промежутке, если fво всех внутренних точках промежутка.

3. Точка х₀ называется точкой минимума функции f(х), если для всех х х₀ из некоторой окрестности точки х₀ выполняется неравенство f f(х₀)

4. Для того чтобы точка х₀ была точкой экстремума функции f(х), необходимо, чтобы эта точка была критической для данной функции.

5. Пусть функция f(х) определена в некоторой окрестности х₀ и дифференцируема в этой точке. Если х₀ - точка экстремума функции f(х), то f

4 этап. Тест № 2. «Задачи - картинки». (Слайд №8-№11)

Задачи и ответы к двум из них заготовлены на карточках и на интерактивной доске. За каждый верный ответ учащиеся получают по одному баллу. Ответы пишутся на карточке, и сдаются учителю. После проведения теста сами учащиеся обсуждают ответы. Учитель ведет комментарий на интерактивной доске маркером.

Тест № 2. «Задачи - картинки». Фамилия, Имя _________________

Вариант II

Вариант I