- Учителю
- Конспект нестандартного урока по геометрии для учащихся 10 классов на тему «Многогранники»
Конспект нестандартного урока по геометрии для учащихся 10 классов на тему «Многогранники»
Конспект нестандартного урока по геометрии на тему
«Многогранники» для 10 класса
Тип урока: урок усвоения новых знаний
Форма урока: урок-лекция
Цели:
Образовательная: ввести определения тела Платона, тела Архимеда, звездчатого многогранника; рассмотреть свойства правильных многогранников; ввести понятие равноугольно полуправильных и звездчатых многогранников; формирование у учащихся знаний истории возникновения и развития теории многогранников.
Развивающая: развитие умений обобщать, абстрагировать и конкретизировать свойства изучаемых объектов и отношений; формирование пространственных представлений учащихся.
Воспитательная: воспитание нравственных качеств личности, аккуратности, добросовестного отношения к работе.
Методы обучения: репродуктивный, эвристический.
Оборудование: плакаты с изображениями фигур, карточки с заданием.
Литература:
-
«Геометрическая рапсодия», Левитин К.Е., М, «Знание», 1976 год.
-
«В мире многогранников», И.М.Смирнова, М, «Просвещение», 1995 год.
-
«Квант» № 5, 1989 год, стр.18.
-
«История математики в школе, IX - X классы», Г.И.Глейзер, М, «Просвещение», 1983 год.
План урока:
-
Организационный момент (2 мин).
-
Актуализация опорных знаний (4 мин).
-
Изучение нового материала и его закрепление(34 мин).
-
Подведение итогов урока (3 мин.).
-
Домашнее задание (2 мин).
Ход урока
1. Организационный момент.
Приветствие учителем класса, проверка отсутствующих и проверка готовности класса к уроку.
Запись на доске и в тетрадях: Число.
Многогранники.
2. Актуализация опорных знаний.
Учитель: Сегодняшний урок посвящен увлекательному разделу геометрии - теории многогранников. Чем привлекательны многогранники? Они обладают богатой историей, которая связана с таким знаменитыми учеными древности, как Пифагор, Евклид, Архимед.
Многогранники были известны в Древнем Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них - пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса - немой трактат по геометрии.

В то же время теория многогранников - современный раздел математики, имеющий практическое приложение в алгебре, теории чисел, в естествознании, в областях прикладной математики - линейном программировании, теории оптимального управления. Прежде, чем приступить к изучению нового материала, давайте кое-что вспомним .
Учитель: Какая фигура называется многогранником?
Ученик: многогранник - совокупность конечного числа плоских в трёхмерном такая, что:
-
каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым (по этой стороне);
-
(связность) от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, к смежному с ним, и т. д.
Учитель: Какие виды многогранников вы знаете?
Ученик: Пирамида, куб, призма, параллелепипед.
Учитель: Что называется призмой, параллелепипедом, пирамидой?
Ученик: Призма - многогранник, у которого две грани - n -угольники (основания П.), а остальные n граней (боковых) - параллелограммы.
Параллелепипед- , основанием которой служит .
Пирамида- , основание которого - , а остальные грани - , имеющие общую вершину.

Учитель: Обратимся к рисунку 3. Данная пространственная фигура называется трехмерной крест. Она состоит из 7 кубов. Почему такая фигура не может быть названа правильной? Сколько квадратов ограничивает ее поверхность? Сколько ребер, вершин и граней у этой фигуры?
Ученик: Эта фигура не является выпуклой, в вершинах многогранника сходится разное число ребер. Фигура имеет 30 граней: у семи кубов 42 грани, у внутреннего куба 6 граней лежат внутри фигуры, и у каждого из остальных шести кубов наружными являются только пять граней. Р = 60, В = 32.
Учитель: Определите, какие из многогранников, изображенных на рисунке, являются выпуклыми и какие невыпуклыми?
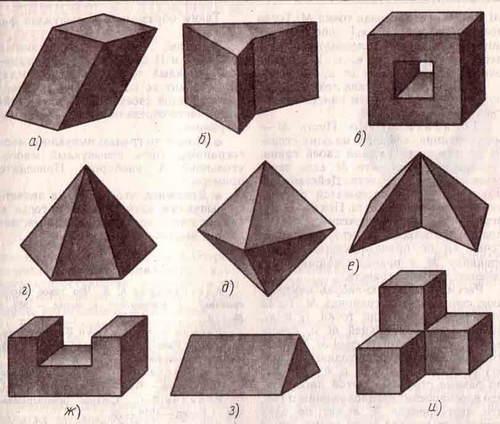
Ученик: а) г) д) з) выпуклые, все остальные нет.
-
Изучение нового материала.
Учитель: Давайте вспомним, какой многоугольник называется правильным?
Ученик: Правильный многоугольник - это , у которого все стороны между собой равны и все углы между собой равны
Учитель: По аналогии давайте попробуем сформулировать определение правильного многогранника.
Ученик: Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон, в каждой вершине многогранника сходится одно и тоже число ребер.
Учитель: Школе Пифагора приписывают открытие существования 5 типов правильных выпуклых многогранников. Позже в своем трактате «Тимей» другой древнегреческий ученый Платон изложил учение пифагорейцев о правильных многогранниках. С тех пор правильные многогранники стали называться Платоновыми телами. Правильным многогранником посвящена последняя, XIII книга знаменитого труда Евклида. Как называется этот труд?
Ученик: «Начала».
Учитель: Существует версия, что Евклид написал первые 12 книг для того, чтобы читатель понял написанную в XIII книге теорию правильных многогранников, которую историки математики называют «венцом «Начал». Здесь установлено существование всех пяти типов правильных многогранников, путей их построения и доказано, что других правильных многогранников не существует. А все-таки, почему же правильных многогранников только пять? Ведь правильных многоугольников на плоскости - бесконечное число. Исследуем возможность существования правильных многогранников. При этом будем опираться на свойство плоских углов многогранного угла. Вспомним Теорему: Сумма плоских углов выпуклого многогранника угла меньше 4d (360о). Рассмотрим всевозможные варианты.
а) Пусть грани правильного многогранника - правильные треугольники. L = 60о.
Если при вершине многогранного угла n плоских углов, то
60о n < 360o ,
n < 6,
n = 3, 4, 5, т.е. существует 3 вида правильных многогранников с треугольными гранями. Как называются эти многогранники?
Ученик: Это тетраэдр, октаэдр, икосаэдр.
Учитель: б) Пусть грани правильного многогранника - квадраты. L = 90о.
Для n - гранных углов n 90о ![]() 360о,
360о,
n ![]() 4,
4,
n = 3, т.е. квадратные грани может иметь лишь правильный многогранник с трехгранными углами, как он называется?
Ученик: куб.
Учитель: в) Пусть грани - правильные пятиугольники
L = 180о (5 - 2) : 5 = 36о*3 = 108о, n*108о ![]() 360о
360о
n*108о ![]() 360о =
360о = ![]() n = 3 - додекаэдр.
n = 3 - додекаэдр.
г) У правильного шестиугольника внутренние углы:
L = 180о * (6 - 2 ) : 6 = 30о * 4 = 120о
В этом случае невозможен даже трехгранный угол. Значит, правильных многогранников с шестиугольными и более гранями не существует.
Записи на доске и в тетрадях:
а) Пусть грани правильного многогранника - правильные треугольники. L = 60о.
Если при вершине многогранного угла n плоских углов, то
60о n < 360o ,
n < 6,
n = 3, 4, 5, т.е. существует 3 вида правильных многогранников с треугольными гранями. Это тетраэдр, октаэдр, икосаэдр.
б) Пусть грани правильного многогранника - квадраты. L = 90о.
Для n - гранных углов n 90о ![]() 360о,
360о,
n ![]() 4,
4,
n = 3, т.е. квадратные грани может иметь лишь правильный многогранник с трехгранными углами - куб.
в) Пусть грани - правильные пятиугольники
L = 180о (5 - 2) : 5 = 36о*3 = 108о, n*108о ![]() 360о
360о
n*108о ![]() 360о =
360о = ![]() n = 3 - додекаэдр.
n = 3 - додекаэдр.
г) У правильного шестиугольника внутренние углы:
L = 180о * (6 - 2 ) : 6 = 30о * 4 = 120о
В этом случае невозможен даже трехгранный угол. Значит, правильных многогранников с шестиугольными и более гранями не существует.
(В процессе урока учащиеся в своих тетрадях заполняют таблицу. ).
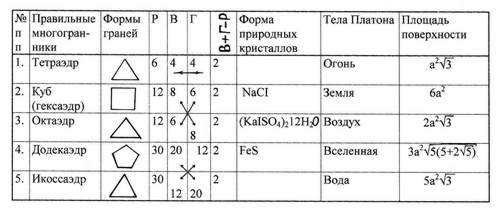
Учитель: Подумаем, почему правильные многогранники получили такие имена?
Ученик: Это связано с числом их граней.
Учитель: В переводе с греческого языка:
эдрон - грань окто - восемь
тетра - четыре додека - двенадцать
гекса - шесть икоси - двадцать
Запись на доске и в тетрадях:
эдрон - грань окто - восемь
тетра - четыре додека - двенадцать
гекса - шесть икоси - двадцать
Учитель: Для всех многогранников подсчитали число В + Г - Р, где В - количество вершин, Р - ребер, Г - граней. Получился один и тот же результат: В + Г - Р = 2. И формула эта верна не только для правильных многогранников. Доказал это соотношение один из величайших математиков Леонард Эйлер (1707 - 1783 гг.), поэтому формула названа его именем. Этот гениальный ученый, родившийся в Швейцарии, почти всю жизнь прожил в России. Современная теория многогранников берет свое начало с его работ.
Учитель: Сравните 2 столбца таблицы В и Г. Что вы заметили?
Ученик: Из таблицы видно, что у куба и октаэдра одно и тоже число ребер, но у куба столько вершин, сколько у октаэдра граней, и, наоборот, у куба столько граней, сколько у октаэдра вершин. Аналогичные соотношения имеют место для додекаэдра и октаэдра.
Учитель: обратите внимание на то, что если центры граней октаэдра принять за вершины другого многогранника, то последний будет кубом. Куб и октаэдр называются взаимно двойственными многогранниками. Взаимно двойственными многогранниками будут также додекаэдр и икосаэдр. Тетраэдр двойственен самому себе.
Учитель: Совершенство форм, красивые математические закономерности, присущие правильным многогранникам, явились причиной того, что им приписывались различные магические свойства. Эти многогранники носят название «платоновских» тел - по имени древнегреческого философа Платона (428 - 348 г. до н.э.), в учении которого они играли важную роль. Тетраэдр символизировал огонь, куб - землю, октаэдр - воздух, икосаэдр - воду, додекаэдр - Вселенную. Его по латыни стали называть «duinta esstntia» («пятая сущность»).
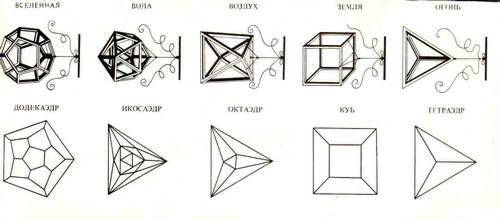
Тетраэдр, куб, октаэдр - это формы имеют природные кристаллы, например: куб - монокристалл алюмокалиевых квасцов ((KАlSO4)2 12 H2O). Существует предположение, что форму додекаэдра древние греки получили, рассматривая кристаллы пирита (сернистого колчедана FeS).
А теперь сосчитаем площадь поверхностей «платоновых тел».
Sтетраэдра = 4 (а2![]() : 4) = а2
: 4) = а2![]() (ед2).
(ед2).
Sкуба = 6а2 (ед2).
Sоктаэдра = 8(а2![]() : 4) = 2а2
: 4) = 2а2![]() (ед2).
(ед2).
Sикосаэдра = 20(а2![]() : 4) = 5а2
: 4) = 5а2![]() (ед2).
(ед2).
(Учащиеся выполняют задания самостоятельно, затем правильность его выполнения проверяется устно).
Записи в тетрадях:
Sтетраэдра = 4 (а2![]() : 4) = а2
: 4) = а2![]() (ед2).
(ед2).
Sкуба = 6а2 (ед2).
Sоктаэдра = 8(а2![]() : 4) = 2а2
: 4) = 2а2![]() (ед2).
(ед2).
Sикосаэдра = 20(а2![]() : 4) = 5а2
: 4) = 5а2![]() (ед2).
(ед2).
Учитель: Мы рассмотрели правильные Платоновы тела и доказали, что их существует не более пяти типов. У правильных многогранников все грани - правильные равные одноименные многоугольники и все многогранные углы равны. Но есть и такие многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные многоугольники. Многогранники такого типа называются равноугольно полуправильными многогранниками. Запишем определение.
Записи на доске и в тетрадях:
Равноугольно полуправильные многогранники - многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные многоугольники.
Учитель: Впервые многогранники такого типа открыл Архимед (287 - 212 гг. до н.э). Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда. Перечислим их.
Тела Архимеда.
Первые пять многогранников очень просто получить из пяти правильных многогранников операцией «усечения», которая состоит в отсечении плоскостями углов многогранника. Если срезать углы правильного тетраэдра плоскостями, каждая из которых отсекает третью часть его ребер, выходящих из одной вершины, то получится усеченный тетраэдр, который имеет восемь граней, из них 4 - правильные шестиугольники и 4 - правильные треугольники, 12 вершин. Многогранник выпуклый, в каждой вершине сходится три ребра. Он называется усеченным тетраэдром. Если указанным образом срезать вершины правильных октаэдра и икосаэдра, получим усеченный октаэдр и усеченный икосаэдр. Обратите внимание, что усеченный икосаэдр очень напоминает изображение футбольного мяча. Из куба и додекаэдра тоже можно получить усеченный куб и усеченный додекаэдр. Их плоскости проходят не через треть ребра. .
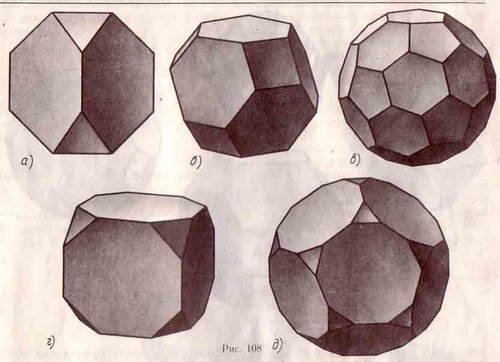
Если теперь в кубе провести плоскости через середины ребер, выходящих из одной вершины, получим еще один шестой равноугольно полуправильный многогранник - кубооктаэдр. Его гранями являются шесть квадратов и восемь правильных треугольников, т.е. грани куба октаэдра, отсюда и название многогранника. Аналогично, если в додекаэдре провести плоскости через середины его ребер, выходящих из одной вершины, получим многогранник, который называется икосадодекаэдром. У него двенадцать граней - правильные пятиугольники, и двадцать - правильные треугольники, т.е. все грани додекаэдра и икосаэдра. К этим двум последним многогранникам также можно применять операцию «усечения» вершин. Получим усеченный кубооктаэдр и усеченный икосадодекаэдр.
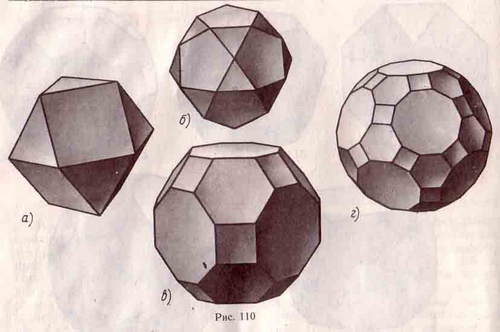
Мы рассмотрели 9 из 13 описанных Архимедом тел. Четыре оставшихся - многогранники более сложного типа. Перечислим их.
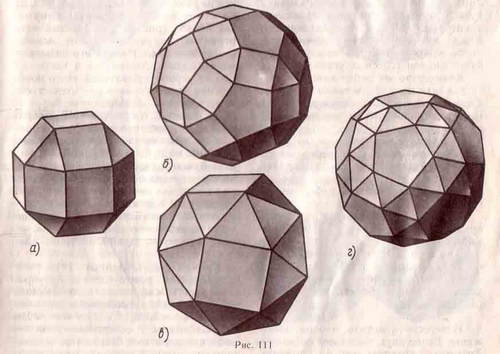
Ромбокубооктаэдр: он состоит из 26 граней, из них 18 квадратов и 8 правильных треугольников;
Ромбоикасодадекаэдр: у него всего 62 грани, из них 30 квадратов, 20 правильных треугольников и 12 правильных пятиугольников;
«плосконосый» куб: у него всего 38 граней, из них 6 квадратов, 32 правильных треугольника:
«плосконосый» додекаэдр: всего 92 грани, из них 12 правильных пятиугольников и 80 правильных треугольников.
В трактате «О многогранниках» Архимед описал каждый полуправильный многогранник, дал его рисунок, а также поставил и решил задачу о количестве многогранных углов и ребер каждого многогранника.
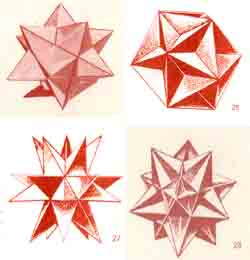
Учитель: Кроме полуправильных многогранников, из правильных многогранников - Платоновых тел можно получить так называемые правильные звездчатые многогранники. Их всего четыре. Первые два были открыты И. Кеплером (1571 - 1630 гг.), а два других были построены почти двести лет спустя французским математиком и механиком Луи Пуансо (1777 - 1859 гг.). Именно поэтому правильные звездчатые многогранники получили название тел Кеплера - Пуансо. Что же они из себя представляют?
В работе «О многоугольниках и многогранниках» (1810 г.) Луи Пуансо перечислил и описал все правильные звездчатые многогранники, поставил, но не решил вопрос о существовании правильных многогранников, число граней которых отлично от 4, 6, 8, 12, 20.
Отчет на этот вопрос был дан год спустя, в 1811 году, французским математиком Огюстом Луи Коши (1789 - 1857 гг.) в работе «Исследование о многогранниках». В ней доказывается, что не существует других правильных многогранников, кроме перечисленных Пуансо. Автор приходит к выводу, что правильные звездчатые многогранники получаются из выпуклых правильных многогранников путем продолжения их ребер или граней, исследуется вопрос, из каких именно правильных многогранников могут быть получены правильные звездчатые многогранники. Делается вывод о том, что тетраэдр, куб и октаэдр не имеют звездчатых форм, додекаэдр имеет три, а икосаэдр - одну звездчатую форму (это малый звездчатый додекаэдр, большой додекаэдр и большой икосаэдр).
Учитель: Число В - Р + Г называется эйлеровой характеристикой многогранника. Эйлерова характеристика выпуклого многогранника равна 2, а для других многогранников она может принимать значения 0; -2; -4; -6.
Учитель: Подсчитайте эйлерову характеристику данного многогранника.
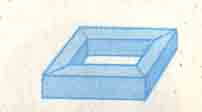
Ученик: Эйлерова характеристика этого многогранника равна нулю
В - 16; Г - 10; Р - 32,
В - Р + Г = 16 - 32 + 16 = 0.
Записи на доске и в тетрадях:
Подсчитайте эйлерову характеристику данного многогранника.

В - 16; Г - 10; Р - 32,
В - Р + Г = 16 - 32 + 16 = 0.
-
Итоги урока.
Учитель: Итак, на уроке мы как бы с высоты сегодняшнего дня рассмотрели историю возникновения и развития теории о правильных многогранниках. Давайте проверим, хорошо ли вы усвоили материал урока. Мой первый вопрос к вам, какая фигура называется правильным многогранником?
Ученик: Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон, в каждой вершине многогранника сходится одно и тоже число ребер.
Учитель: сколько существует типов Платоновских тел?
Ученик: Мы рассмотрели правильные Платоновы тела и доказали, что их существует не более пяти типов.
Учитель: А что за равноугольно полуправильные многогранники и кто их открыл?
Ученик: Равноугольно полуправильные многогранники - многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные многоугольники. Открытие принадлежит Архимеду.
Учитель: Что называется эйлеровой характеристикой, и чему равна Эйлерова характеристика выпуклого многогранника?
Ученик: Число В - Р + Г называется эйлеровой характеристикой многогранника. Эйлерова характеристика выпуклого многогранника равна 2, а для других многогранников она может принимать значения 0; -2; -4; -6.
5. Домашнее задание.
Учитель: Вашим домашним заданием будет следующее: «Геометрия 10 - 11», Л.С. Атанасян и др., М, «Просвещение», 2001 год стр. 68 - 71, задача: Какое минимальное количество точек на поверхности
а)(2) додекаэдра,
б)(5) икосаэдра
надо отметить, чтобы на каждой грани была хотя бы одна отмеченная точка?
Решение домашнего задания:
а) Поскольку у додекаэдра 12 граней и каждая его вершина принадлежит трём из них, искомый минимум не меньше 4. На рисунке 1а показано, что можно отметить 4 вершины, тем самым, минимум равен 4.
б) Шести вершин, выделенных на рисунке 1б, достаточно. Докажем, что пяти вершин недостаточно. Пусть найдутся пять вершин, удовлетворяющих условию задачи. Удалим из графа рёбер и вершин икосаэдра все рёбра, кроме тех, которые соединяют какие-либо две из пяти выбранных вершин. Рассмотрим одну компоненту связности получившегося графа. Первая вершина покрывает 5 граней, а все остальные - не более чем по 3 новых. Если компонент связности не более двух, то всего покрывается не более 5 + 5 + 3 + 3 + 3 = 19 граней, а этого недостаточно. Значит, найдётся компонента связности из одной вершины. Пусть это вершина A. Тогда вершины B, C, D, E и F не входят в число выбранных пяти вершин. Но из оставшихся шести вершин невозможно выбрать четыре так, чтобы получить две компоненты связности. Пришли к противоречию.
11