Задания ОГЭ. Раздел: геометрия

1. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.

2. Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.

3. Касательные в точках A и B к окружности с центром O пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.

4. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=38°. Найдите угол NMB. Ответ дайте в градусах.

5. К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.

6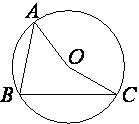. Точка O - центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.

7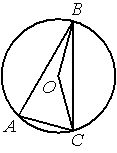. Точка О - центр окружности, ∠BOC=160° (см. рисунок). Найдите величину угла BAC (в градусах).

8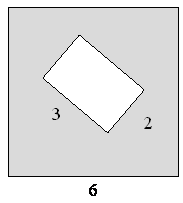. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

9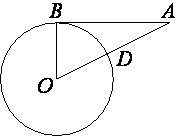. Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

10. В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.

1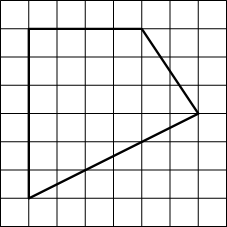1. Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.

1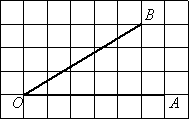2. Найдите тангенс угла AOB, изображённого на рисунке.

13. Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.

1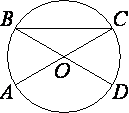4. В окружности с центром O отрезки AC и BD - диаметры. Центральный угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.

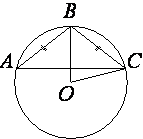
15. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=177°. Найдите величину угла BOC. Ответ дайте в градусах.

16. В окружности с центром O отрезки AC и BD - диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.