- Учителю
- Конспект урока по геометрии в 8 классе «Применение формулы Пика»
Конспект урока по геометрии в 8 классе «Применение формулы Пика»
Конспект урока по геометрии в 8 классе «Применение формулы Пика»
Учитель математики МАОУ Видновской гимназии Кондратьева Т.Ю.
«Ты имеешь собственное мнение, но если
спросишь у другого - будет выбор»
На предыдущих уроках мы ввели понятие площади многоугольника, узнали, как она обозначается, и познакомились с единицами измерения площади, перечислили свойства площадей. А теперь научимся все наши знания использовать на примерах решения задач.
Задание. Найти площадь данного треугольника.
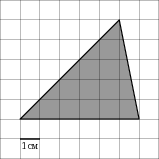
Какие способы вы можете предложить?

1. Площадь - величина положительная.
2. Равные многоугольники имеют равные площади.
Например, если рассмотреть изображенные на Рис. 1 равные четырехугольники (![]() и
и ![]() ), то их площади будут равны
), то их площади будут равны ![]() .
.

Рис. 1
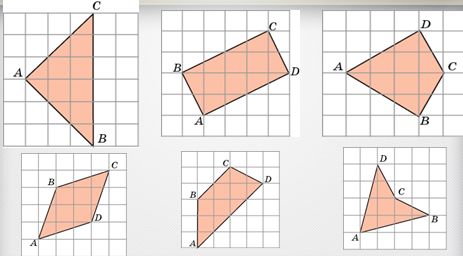
3. Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей данных многоугольников.
Например, дана трапеция ![]() (см. Рис. 2), которую высотами разбили на три фигуры: треугольник
(см. Рис. 2), которую высотами разбили на три фигуры: треугольник ![]() , прямоугольник
, прямоугольник ![]() и треугольник
и треугольник ![]() . Тогда площадь трапеции:
. Тогда площадь трапеции: ![]() .
.
Рис. 2
4. Площадь квадрата равна квадрату его стороны, т.е. если сторона квадрата равна ![]() , то
, то ![]() .
.
Например, рассмотрим квадрат ![]() (см. Рис. 3).
(см. Рис. 3).
Рис. 3
Если сторона квадрата ![]() , то его площадь
, то его площадь ![]() .
.
Пример 3. Найти сторону квадрата, если его площадь равна: а) 81 см2; б) 2,25 дм2.
Решение. Для решения обоих пунктов достаточно применить четвертое свойство площади ![]() .
.
а) ![]() ;
;
б) ![]() .
.
Ответ: а) ![]() ; б)
; б) ![]() .
.
Вернемся к нашей задаче.
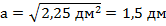
И конечно можно использовать формулу для вычисления площади.
Возникает вопрос: в чём заключается особенность задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге. Такие задачи встречаются в контрольно - измерительных материалах ЕГЭ и ГИА. Попробуем рассмотреть задачи на клетчатой бумаге, связанные с нахождением площади изображённой фигуры.
Решетки .Узлы.
Рассмотрим на плоскости два семейства параллельных прямых, разбивающих плоскость на равные квадраты; множество всех точек пересечения этих прямых называется точечной решеткой или просто решеткой , а сами точки -узлами решетки.

Внутренние узлы многоугольника - красные.
Узлы на гранях многоугольника - синие.
Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S - площадь многоугольника, В - число клеток, которые целиком лежат внутри многоугольника, и Г - число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку 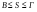 .
.
Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги - в таких, где пересекаются линии сетки.
Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника.
Теперь мы знаем несколько способов вычисления площадей фигур. Предложите способ, на ваш взгляд более удобный для данной фигуры.
Вот несколько заданий из открытого банка заданий ГИА и ЕГЭ.
(устная фронтальная работа)
Исследование площадей многоугольников.
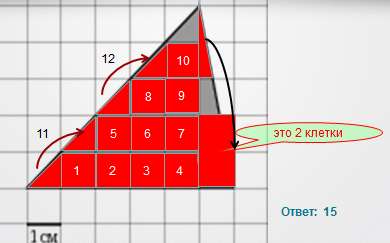
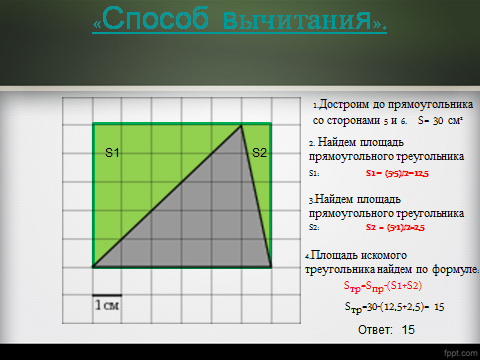
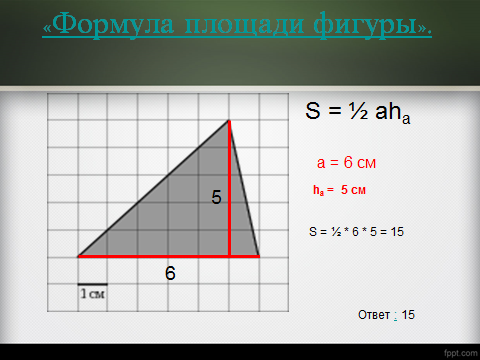
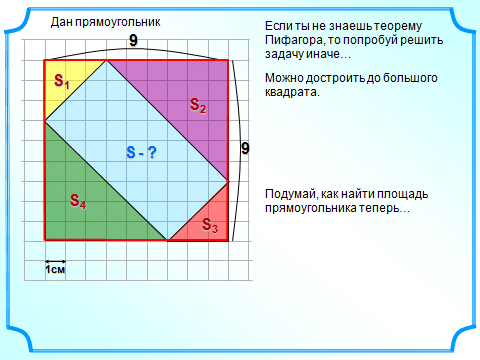
1) На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник.Найдите его площадь в квадратных сантиметрах
Рисунок
По формуле геометрии
По формуле Пика
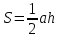
a=6; h=5.
S=1/2 6
6 5=15
5=15

Г=12 ; B=10 . S=10+12/2 -1=15
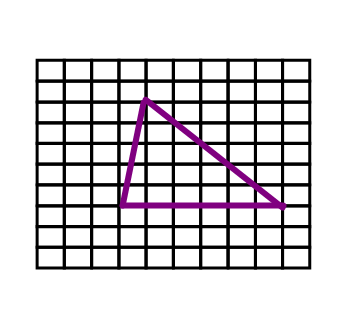
Sтр.ABD=1/2 AD BD=1/2
BD=1/2 2
2 1=1
1=1
Sтр.BDC=1/2 DC  BD=1/2
BD=1/2 3
3 1=1,5
1=1,5
Sтр.ABC=Sтр.BDC-Sтр.ABD=
1,5-1=0,5

Г=3 ;В=0.
S=0+3/2-1=0,5
S1=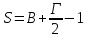 b=1/2
b=1/2 7
7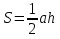 3,5
3,5
S2=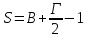 b=1/2
b=1/2 7
7 2=7
2=7
S3=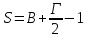 b=1/2
b=1/2 4
4 1=2
1=2
S4=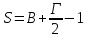 b=1/2
b=1/2 5
5 1=2,5
1=2,5
S5=a²=1²=1
Sкв.= a²=7²=49
S=49-3.5-7-2-2,5-1=32см²

Г=5;В=31.
S=31+ -1=32см²
-1=32см²
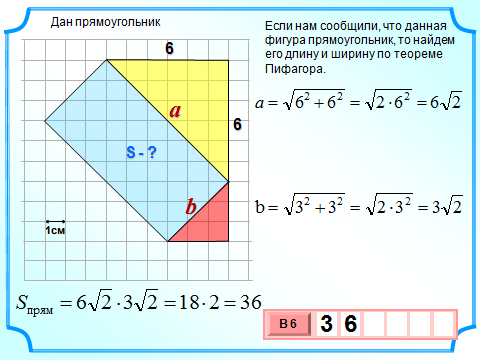
S=a


S= =36 см2
=36 см2

Г=18, В=28
S=28+ -1=36см2
-1=36см2
S1=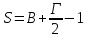 b=1/2
b=1/2 3
3 3=4,5
3=4,5
S2=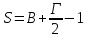 b=1/2
b=1/2 6
6 6=18
6=18
S3=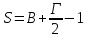 b=1/2
b=1/2 3
3 3=4,5
3=4,5
S=4,5+18+4,5=27 см²

Г=18;В=28.
S=28+ -1=36см²
-1=36см²
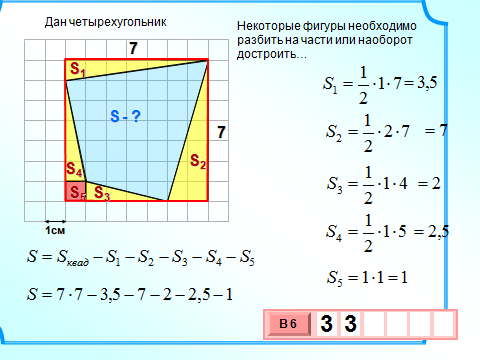
S1=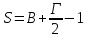 b=1/2
b=1/2 3
3 3=4,5
3=4,5
S2=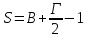 b=1/2
b=1/2 6
6 6=18
6=18
S3=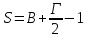 b=1/2
b=1/2 3
3 3=4,5
3=4,5
S4=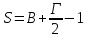 b=1/2
b=1/2 6
6 6=18
6=18
Sкв.=9²=81см²
S=81-4,5-18-4,5-18=36см²

Г=18;В=28.
S=28+ -1=36см²
-1=36см²
S1=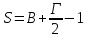 b=1/2
b=1/2 2
2 4=4
4=4
S2=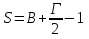 =1/2
=1/2 4
4 4=8
4=8
S3=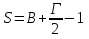 =1/2
=1/2 8
8 2=8
2=8
S4=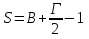 =1/2
=1/2 4
4 1=2
1=2
Sпр.=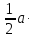 b=6
b=6 8=48
8=48
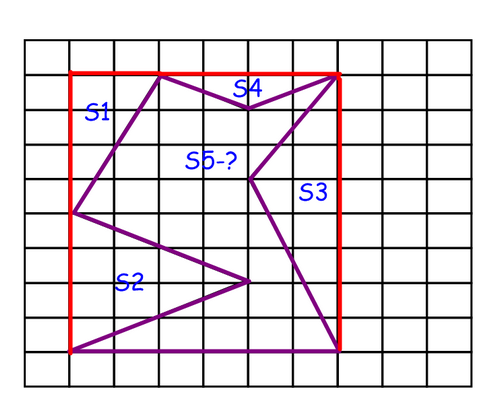
S5=48-4-8-8-2=24 см²

Г=16;В=17.
S=17+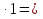 -1=24 см²
-1=24 см²
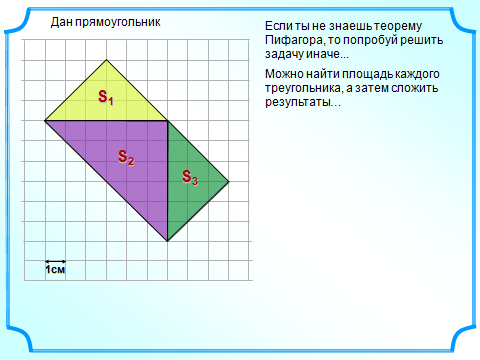
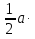
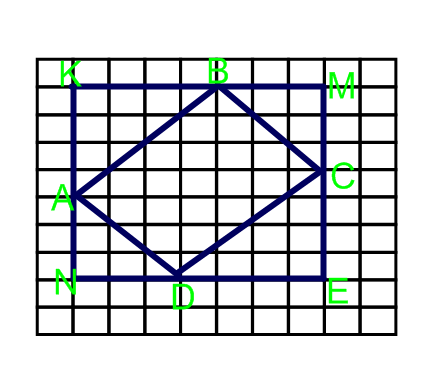
Sкв.KMNE=7 7=49
7=49
Sтр.AKB=1/2 KB
KB AK=1/2
AK=1/2 4
4 4=8
4=8
Sтр.AKB=Sтр.DCE=8
Sтр.AND= 1/2 ND
ND AN=1/2
AN=1/2 3
3 3=4,5
3=4,5
Sтр.AND=Sтр.BMC=4,5
Sпр.= Sкв.KMNE- Sтр.AKB- Sтр.DCE- Sтр.AND- Sтр.BMC=49-8-8-4,5-4,5=24

Г=14;В=19.
S=18+14/2-1=24
Вывод
Сравнив результаты в таблицах и доказав теорему Пика, мы пришли к выводу ,что площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по выведенной формуле планиметрии
Учащимся раздаются индивидуальные карточки с формулой Пика и таблица в русским алфавитом. На доске отображена таблица с количеством ячеек, соответствующим количеству карточек.
В результате выполнения работы в таблице должно быть расшифровано слово.
Карточки.
Формула Пика
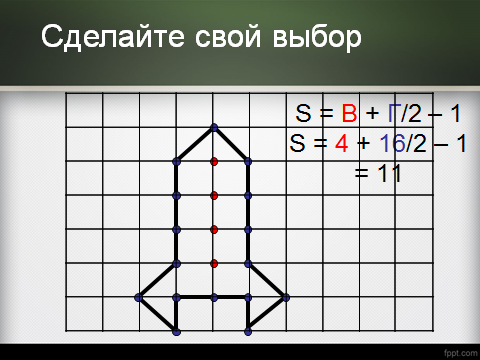
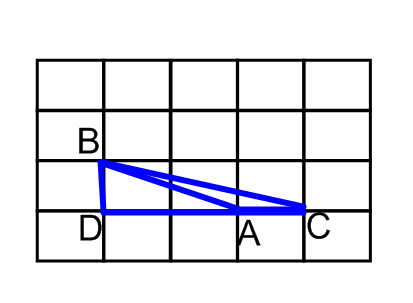
Площадь многоугольника с целочисленными вершинами равна В + Г/2 − 1, где В есть количество целочисленных точек внутри многоугольника, а Г - количество целочисленных точек на границе многоугольника.
Пример.
В = 10, Г = 6, В + Г/2 − 1 = 10 + 6:2 − 1 = 12
КАРТОЧКА 1
Ответ:
КАРТОЧКА 2
Ответ:
.КАРТОЧКА 3
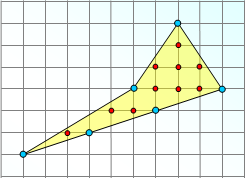
Ответ:
КАРТОЧКА 4

Ответ:
КАРТОЧКА 5

Ответ:
КАРТОЧКА 6

Ответ:
КАРТОЧКА 7
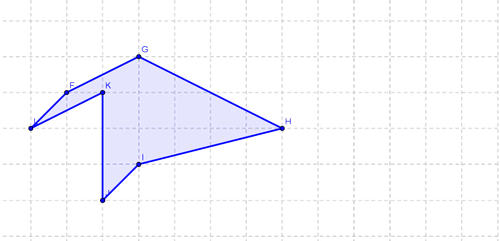
Ответ:
КАРТОЧКА 8
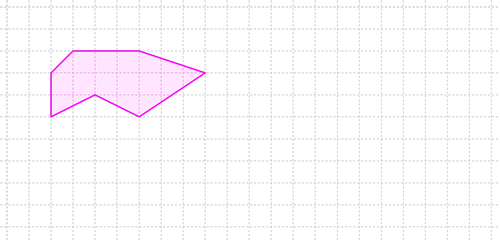
Ответ:
КАРТОЧКА 9

Ответ:
1
2
3
4
5
6
7
8
9
А
Б
В
Г
Д
Е
Ё
Ж
З
10
11
12
13
14
15
16
17
18
И
Й
К
Л
М
Н
О
П
Р
19
20
21
22
23
24
25
26
27
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
28
29
30
31
32
33
Ь
Ы
Ъ
Э
Ю
Я

Список литературы
1.Геометрия на клетчатой бумаге. Малый МЕХмат МГУ.
2.Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
3.Задачи открытого банка заданий по математике ФИПИ, 2010 - 2011
4.В.В.Вавилов, А.В.Устинов .Многоугольники на решетках.М.МЦНМО,2006.
5.Математические этюды.
6.Л.С.Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.Геометрия .7-9 классы.М. Просвещение ,2010
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
-
Planetcalc.ru ().
-
Dcs.isa.ru ().