Внеклассная работа по математике. Математический турнир

Внеклассная работа по математике.

Математический турнир.

Моисеева Светлана Эдуардовна,

учитель математики МОУ СОШ № 10

г. Дубны Московской области.

Внеклассная работа - это неотъемлемая часть учебно-воспитательного процесса. Очень часто именно на внеклассных мероприятиях, в свободной, раскрепощённой игровой обстановке наиболее полно раскрывается творческий потенциал учащихся, и то, что на уроках казалось трудным, и даже непосильным в процессе игры становится понятным и доступным.

Наиболее важными задачами внеклассной работы являются следующие:

- пробуждение и развитие устойчивого интереса к математике;

- расширение кругозора и углубление знаний учащихся;

- развитие математических способностей и логического мышления у учащихся;

- общий подъём математической культуры, интеллектуального уровня учащихся;

- развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой;

- расширение представлений учащихся о практическом применении математики;

- осуществление индивидуализации и дифференциации;

- разностороннее развитие личности.

Внеклассная работа может осуществляться в самых разнообразных видах и формах. Одним из основных её видов является массовая работа, то есть эпизодическая работа, проводимая с большим детским коллективом.

Одной из самых популярных форм внеклассной работы является неделя (декада) математики. В план проведения недели могут быть включены викторины, конкурсы, турниры, олимпиады, бои, КВН, вечера для старшеклассников, научно-практическая конференция, выпуски стенгазет и т.д.

Примером мероприятия, которое можно включить в программу предметной недели, может служить математический турнир для учащихся 8 классов. Далее представлены материалы для его проведения.

«Математический турнир» между командами 8 классов

Оптимальное количество участников - 3 команды по 6-7 человек. В качестве судей - старшеклассники.

1. Представление команд. Каждая команда должна заранее подготовиться - продумать название, девиз, эмблему. Максимальный балл - 3.

2. Разминка. В быстром темпе задаются вопросы по теме «Четырёхугольники» - по 1 вопросу каждому участнику: первому участнику первой команды, второму участнику второй команды и так далее по кругу. Если участник даёт неверный ответ, то право ответа переходит к очередному участнику следующей команды. Каждый верный ответ приносит команде 1 балл.

Вопросы для разминки

1. Верно ли, что в параллелограмме сумма противоположных углов 180°?

2. Сколько вершин у четырёхугольника?

3. Верно ли, что прямоугольник-это параллелограмм, у которого один угол прямой?

4. Существует ли параллелограмм, у которого диагонали перпендикулярны?

5. Верно ли, что квадрат - это параллелограмм, у которого диагонали равны?

6. Сколько диагоналей можно провести в треугольнике?

7. Может ли квадрат иметь диагонали разной длины?

8. Верно ли, что квадрат - это ромб, у которого углы прямые?

9. Сколько пар параллельных сторон у трапеции?

10. У какого параллелограмма диагонали перпендикулярны?

11. Верно ли, что в параллелограмме противоположные углы равны?

12. Правда ли, что ромб - это параллелограмм, у которого смежные стороны равны?

13. Сколько диагоналей можно провести в четырёхугольнике?

14. Верно ли , что если у трапеции диагонали равны, то она равнобедренная?

15. Можно ли утверждать, что если в четырёхугольнике 2 стороны параллельны, то это - параллелограмм?

16. Верно ли, что диагонали прямоугольника являются биссектрисами его углов?

17. Может ли прямоугольная трапеция быть равнобедренной?

18. Верно ли, что в ромбе противоположные стороны равны?

19. Правда ли, что квадрат- это прямоугольник, у которого стороны равны?

20. Существует ли трапеция, у которой диагонали перпендикулярны?

21. Верно ли, что в трапеции углы при основании равны?

3. «Третий лишний». Предлагается три серии графиков ранее изученных функций, по три графика в каждой серии, среди которых необходимо выбрать «лишние». Например, две гиперболы, одна парабола или графики линейных функций, два из которых расположены под острым углом к оси абсцисс, а один - под тупым и т. п. Каждый верно выбранный «лишний» график - 1 балл.

4. Восстановление «древних» свитков (вставить пропущенные слова в стихотворениях).

Ведущий объясняет, что при раскопках древнего города были обнаружены свитки с математическими текстами, в которых, к сожалению, некоторые слова не удалось восстановить, и все лучшие умы человечества с надеждой ожидают разгадки от участников турнира. Каждое правильно подобранное слово - 1 балл.

Гимн ________________

Как символ вечного союза,

Как верной дружбы знак простой,

Связала ты, ____________,

Навеки _________ собой.

Скрывала тайну ты, но скоро

Явился некий мудрый грек

И теоремой___________

Тебя прославил он навек.

Хранит тебя, безмолвно, чинно

Углов сторожевой наряд,

И копья - острые_________

На обе стороны грозят.

И если двоечник, конфузясь,

Немеет пред твоим лицом.

Пронзит его,__________,

Своим отточенным копьем.

__________________

_________ обмяк, устал,

Дал за углы себя схватить,

И _________ стал.

И загрустил:

А вдруг бы жизнь

другим путём пошла,

Имей я два других ______

5. Вопросы командам соперников (домашние заготовки). Оцениваются как вопросы, так и ответы. Каждый заданный вопрос и каждый правильный ответ - 1 балл. Дополнительные баллы могут быть присуждены за оригинальность вопросов и ответов.

6. «Объясни термин». Участникам предлагается объяснить значение 10 математических терминов: гипотенуза, асимптота, абсцисса, медиана, экспонента, ордината, синусоида, биссектриса, аппликата, пирамида. Поскольку восьмиклассником известны не все из них, то оценивать нужно не только правильные ответы, но и проявленную находчивость и чувство юмора.

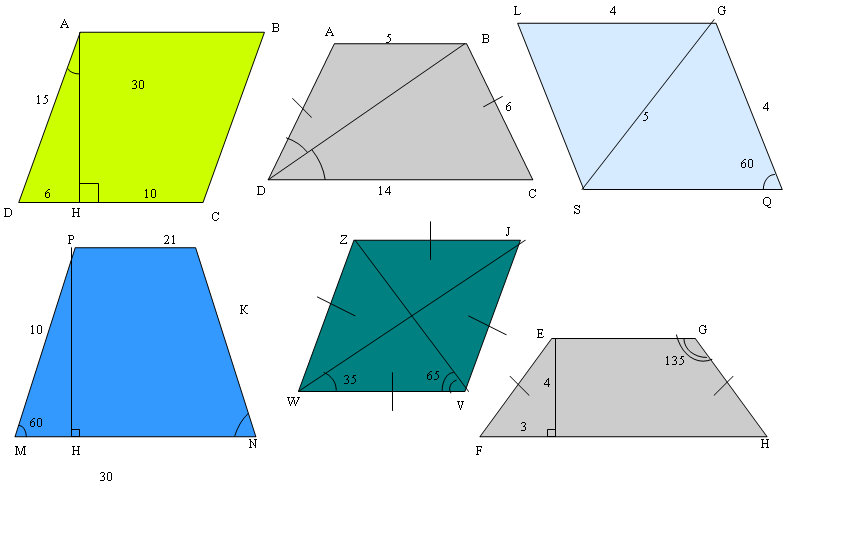7. «Найди ошибку». На чертежах четырёхугольников допущены ошибки, которые нужно найти, опираясь на свойства четырёхугольников. Указание на ошибку оценивается одним баллом, обоснование - ещё одним.

8. Эстафета. Нужно выполнить преобразования рациональных выражений, используя ответ, полученный предыдущим игроком. Каждое верно выполненное действие - 1 балл.

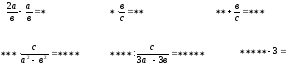
1) 2) 3)

4) 5) 6)

9. Подведение итогов. Награждение команд.

При проведении внеклассных мероприятий важно учитывать эмоциональную составляющую. Для наиболее эффективного достижения целей, поставленных перед каждым мероприятием необходимо сохранять позитивный настрой, свободу творчества при ненавязчивом руководстве учителя. Чтобы каждый ребёнок мог почувствовать уверенность в своих силах, задания должны быть посильными. Соревновательный дух придаёт азарт и повышает интерес. А чтобы результаты не принесли разочарования проигравшей команде, нужно сделать так, чтобы проигравших не было вовсе. Для этого награждение можно проводить по номинациям (сколько команд, столько номинаций).