План урока геометрии на тему: Отображение плоскости на себя. Движения. Виды движения.

План урока геометрии в 9 классе

на тему «Отображение плоскости на себя. Движения. Виды движения.»

Цели урока:

• ввести понятие отображения плоскости на себя и движения;

• рассмотреть виды движений - осевую симметрию, центральную симметрию, параллельный перенос, поворот;

• рассмотреть простейшие задачи на построение образов фигур при преобразованиях симметрии относительно прямой и центра; параллельном переносе; повороте

• совершенствовать навыки систематизации и обобщения материала, умений использовать чертежные инструменты;

• развивать коммуникативные навыки учащихся при групповой работе, развивать математическую речь.

Ход урока.

1 Вызов.

Сегодня я познакомлю вас с творчеством известного голландского художника Маурица Корнелиса Эшера. Эшер был нашим современником и умер в 1971 году, прожив 73 года. Он создал уникальные и очаровательные работы, в которых использован широкий круг математических идей. Среди его восторженных поклонников были и математики, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это более интересно тем, что сам Эшер не имел специального математического образования. Без его гравюр не обходится с середины прошлого века ни одна «иллюстрированная» книга по математике, физике, топологии, не говоря уж о популярных изданиях! (Кстати, советский научно-популярный журнал «Квант» публиковал Эшера свыше 20 раз, «Знание-сила» - еще больше.)

Посмотрите на его работы и попытайтесь ответить на вопрос: «Какие математические понятия можно увидеть в его работах?» Презентация.

(Учащиеся обсуждают в группах и пытаются ответить на поставленный вопрос.)

Мне кажется, что в конце урока мы сможем более точно ответить на поставленный вопрос.

2. Осмысление. (Стратегия «Зигзаг»).

Учитель: Тема нашего сегодняшнего урока «Отображение плоскости на себя. Движения. Виды движения.» Некоторые аспекты данной темы вам уже знакомы, с другими вам предстоит познакомиться на этом уроке.

Представим себе, что каждой точке плоскости сопоставляется (т. е. ставится в соответствие) какая-то точка этой же плоскости, причём любая точка плоскости оказывается сопоставленной некоторой точке. Тогда говорят, что дано отображение плоскости на себя. Фактически, не вводя это понятие, мы уже встречались с отображениями плоскости на себя, когда изучали осевую и центральную симметрию.

Сегодня, работая в группах, вы вспомните ранее изученный материал и познакомитесь с другими видами отображения плоскости на себя. В результате этой работы вы должны научиться сами и научить своих одноклассников строить фигуры при различных видах отображений , составить схему, объединяющую весь материал урока и представить её всему классу.

1.Учащиеся выбирают себе текст для самостоятельной работы и начинают над ним работать. (10 мин.)

2. Далее переходят в экспертные группы и обсуждают выполнение задания №3. (5мин).

3. Возвращаются в рабочие группы и объясняют своим товарищам свою часть материала.(10 мин.) У всех учащихся в тетради должно быть построено отображение отрезка при всех видах отображений.

3. Рефлексия.

4. Составляют кластер, выполняя задание: Для понятий «Отображение плоскости на себя», «Движения», Осевая симметрия», «Центральная симметрия», «Параллельный перенос», «Поворот» с помощью стрелок установить соответствие.(5 мин.). Оформляют на листах. Отчитываются у доски. Учитель добавляет стрелки для продолжения работы дома.

Возвращаемся к работам Эшера и отвечаем на поставленный в начале урока вопрос.

5. Заполнение листа самооценки.

Учитель (при наличии времени): показать видеоролики с диска «Уроки геометрии в 9 классе», раздел «Параллельный перенос и поворот»

Домашнее задание.

1. П. 113-117.

2. Построить отображение треугольника при различных видах движения.

3. Найти ответы на поставленные при составлении кластера вопросы.

При составлении презентации к уроку были использованы слайды презентации учителя математики Савченко ЕМ.

Параллельный перенос.

1. Представим себе, что каждой точке плоскости сопоставляется (ставится в соответствие) какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. Тогда говорят, что дано отображение плоскости на себя. Примером такого отображения является параллельный перенос.

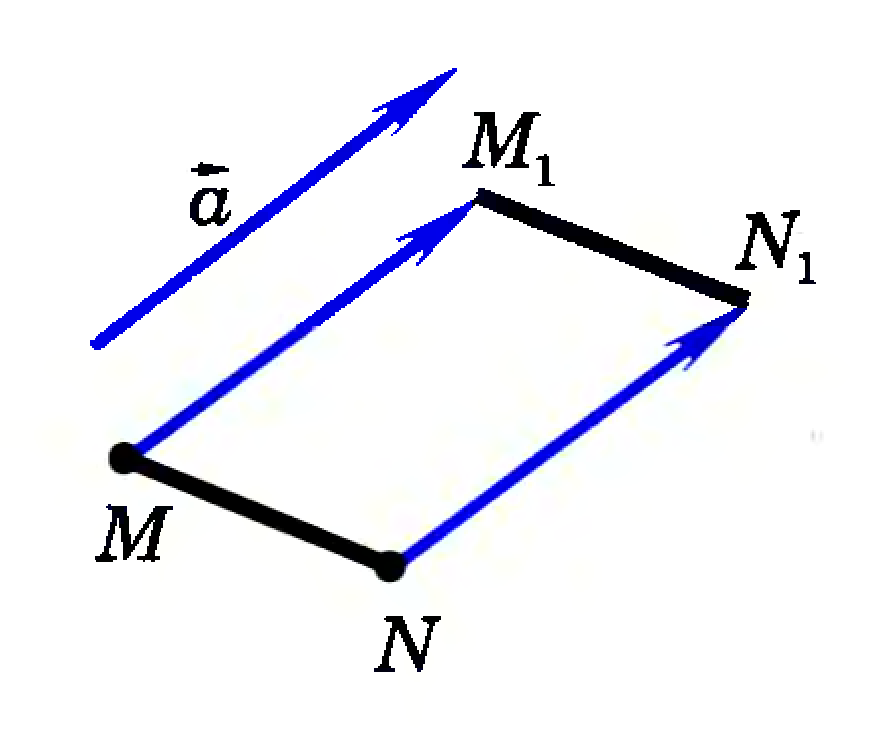
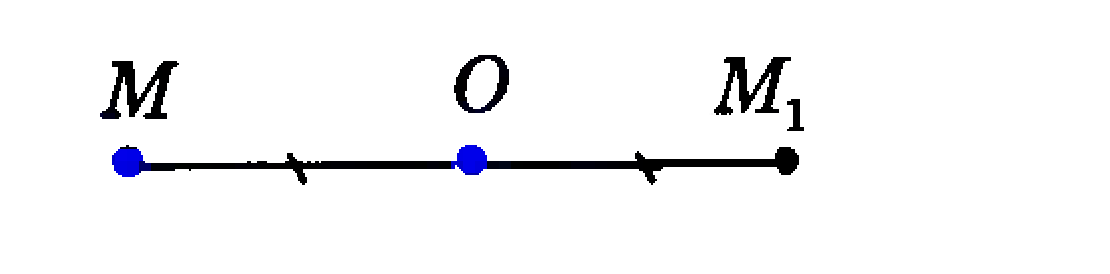
В самом деле, пусть а - данный вектор. Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку M₁, что вектор ММ₁ равен вектору (см. рис).

Задание 1.

Изучи теорию. Запиши в тетрадь определение основных понятий. Выполни построение точки М₁, которая получается при параллельном переносе точки М на вектор .

Параллельный перенос обладает следующим важным свойством - это отображение плоскости на себя, которое сохраняет расстояния между точками. Любое отображение, обладающее этим свойством, называется движением (или перемещением). Итак, движение плоскости - это отображение плоскости на себя, сохраняющее расстояния.

Итак, параллельный перенос является движением, т. е. отображением плоскости на себя, сохраняющим расстояния.

Задание 2.

Построй в тетради и запиши алгоритм построения отрезка, который получится при параллельном переносе отрезка MN данный вектор .

Задание 3.

Построить самостоятельно и обсудить в группе построение треугольника, получаемого при параллельном переносе на данный вектор.

Осевая симметрия.

1. Представим себе, что каждой точке плоскости сопоставляется (ставится в соответствие) какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. Тогда говорят, что дано отображение плоскости на себя. Примером такого отображения является осевая симметрия.

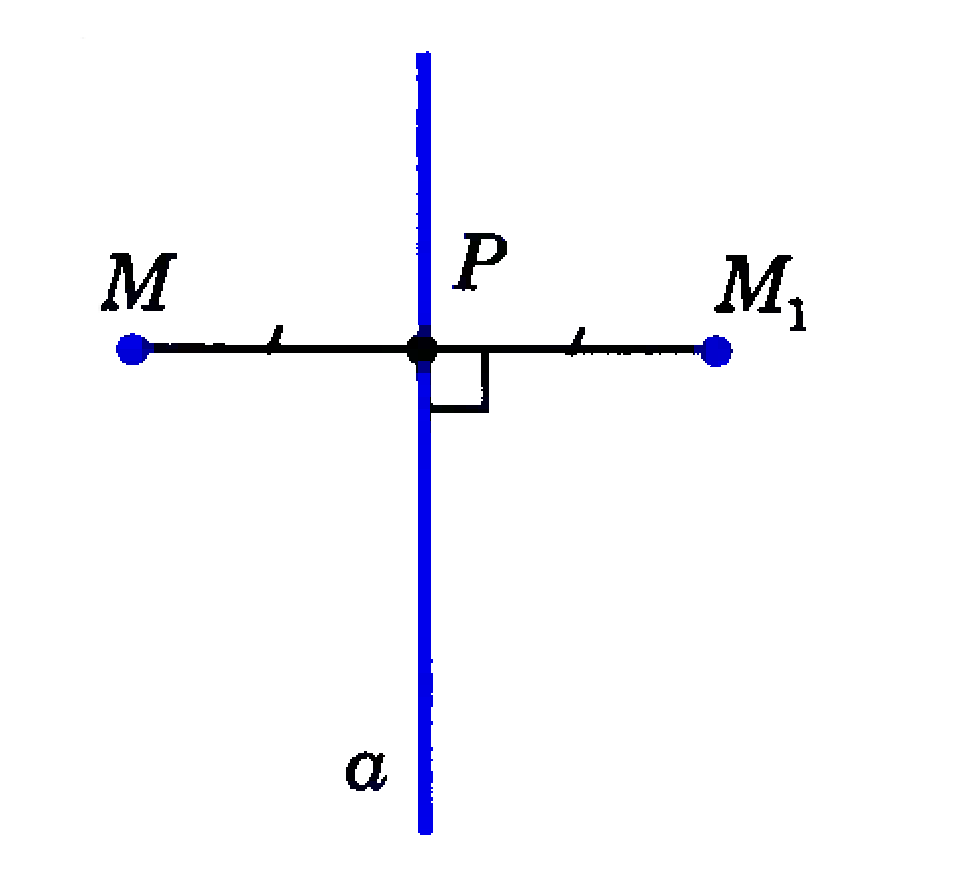
В самом деле, пусть а - ось симметрии (см. рис.). Возьмем произвольную точку М, не лежащую на прямой а, и построим симметричную ей точку М₁ относительно прямой а. Для этого нужно провести перпендикуляр МР к прямой а и отложить на прямой МР отрезок PM₁, равный отрезку МР, так, как показано на рисунке . Точка М₁ и будет искомой. Если же точка М лежит на прямой а, то симметричная ей точка М₁ совпадает с точкой М. Мы видим, что с помощью осевой симметрии каждой точке М плоскости сопоставляется точка М₁ этой же плоскости. При этом любая точка М₁ оказывается сопоставленной некоторой точке М. Итак, осевая симметрия представляет собой отображение плоскости на себя.

Задание 1.

Изучи теорию. Запиши в тетрадь определение основных понятий. Выполни построение точки, симметричной данной относительно прямой.

Осевая симметрия обладает следующим важным свойством - это отображение плоскости на себя, которое сохраняет расстояния между точками. Любое отображение, обладающее этим свойством, называется движением (или перемещением). Итак, движение плоскости - это отображение плоскости на себя, сохраняющее расстояния.

Задание 2.

Построй в тетради и запиши алгоритм построения отрезка, симметричного данному относительно данной прямой.

Построение отрезка, симметричного данному относительно данной прямой.

Задание 3.

Построить самостоятельно и обсудить в группе построение треугольника, симметричного данному относительно данной прямой.

Задание 4.

В экспертной группе выполнить коллективную работу по построению треугольника, симметричного данному, относительно данной прямой.

Задание 5.

1) Вернуться в рабочую группу и объяснить одноклассникам свою часть материала. У всех в тетрадях должно быть построено отображение отрезка при всех видах движения.

2) Составить кластер, выполняя задание: С помощью стрелок установить соответствие между понятиями «Отображение плоскости на себя», «Движения», Осевая симметрия», «Центральная симметрия», «Параллельный перенос», «Поворот». Оформить на листах. Отчитаться у доски.

Поворот.

1. Представим себе, что каждой точке плоскости сопоставляется (ставится в соответствие) какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. Тогда говорят, что дано отображение плоскости на себя. Примером такого отображения является поворот.

Отметим на плоскости точку О (центр поворота) и зададим угол α (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку M₁ что ОМ = ОМ₁

и <МОМ₁ = а (см.рис.).

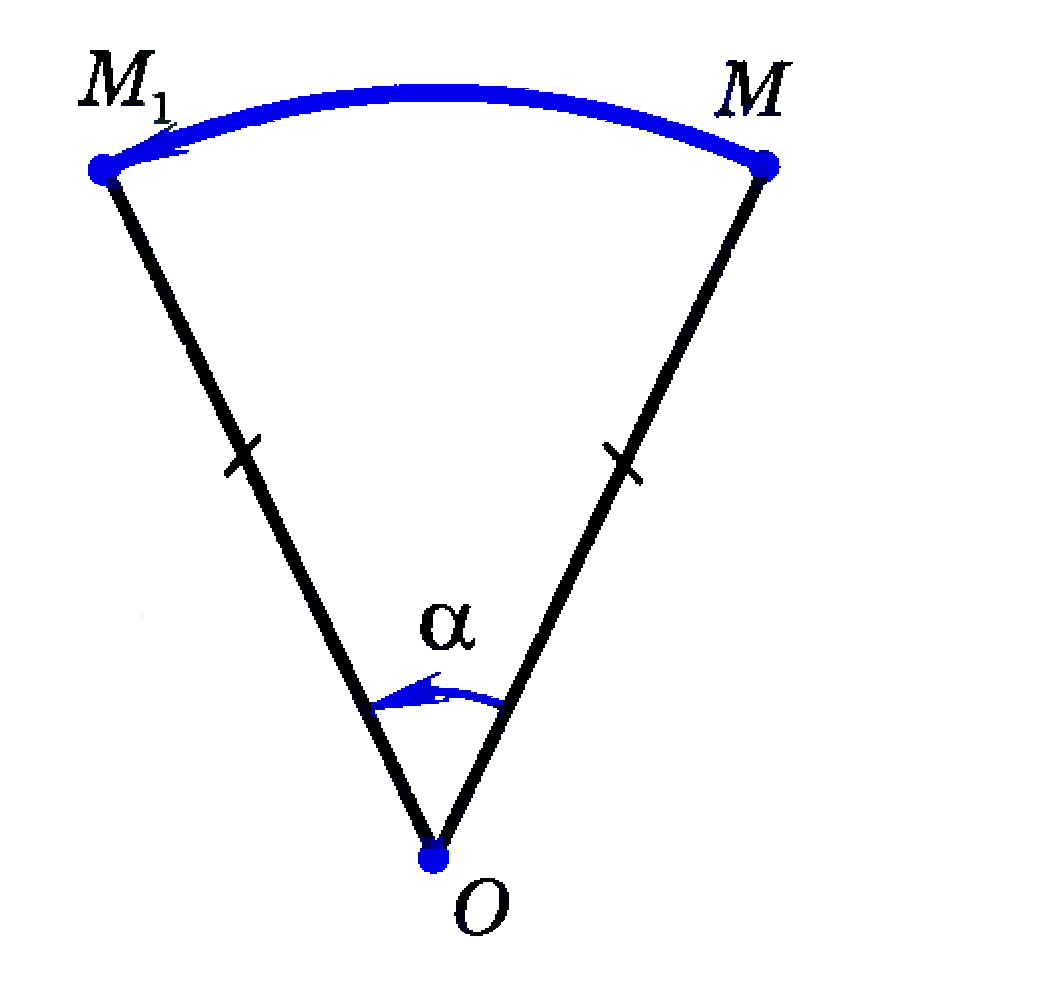
При этом точка О остается на месте, т. е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении - по часовой стрелке или против часовой стрелки. На рисунке изображен поворот против часовой стрелки.

Задание 1.

Изучи теорию. Запиши в тетрадь определение основных понятий. Выполни построение точки, получаемой при повороте вокруг точки О на 60 ⁰против часовой стрелки..(см. рис.)

Поворот обладает следующим важным свойством - это отображение плоскости на себя, которое сохраняет расстояния между точками. Любое отображение, обладающее этим свойством, называется движением (или перемещением). Итак, движение плоскости - это отображение плоскости на себя, сохраняющее расстояния.

Задание 2.

Построй в тетради и запиши алгоритм построения отрезка M₁ N₁, получаемого при повороте отрезка MN вокруг точки О на угол 30⁰ против часовой стрелки (см. рис.).

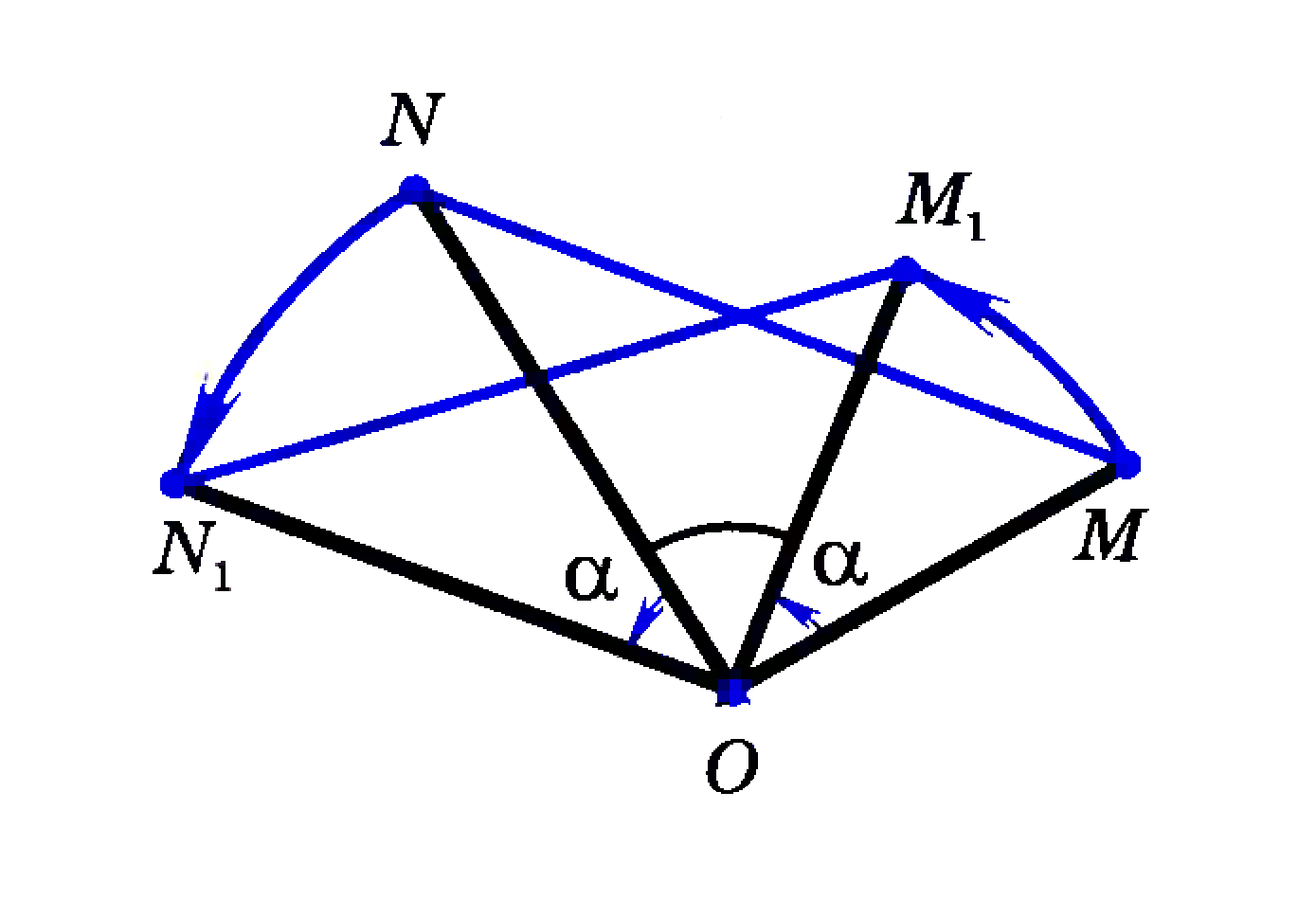
Задание 3.

Построить самостоятельно и обсудить в группе построение треугольника A ₁B ₁C ₁, получаемого при повороте треугольника ABC вокруг точки О на угол 60⁰ по часовой стрелке.

Задание 4.

В экспертной группе выполнить коллективную работу по построению треугольника A ₁B ₁C ₁, получаемого при повороте треугольника ABC вокруг точки О на угол 60⁰ по часовой стрелке.

Задание 5.

1) Вернуться в рабочую группу и объяснить одноклассникам свою часть материала. У всех в тетрадях должно быть построено отображение отрезка при всех видах движения.

2) Составить кластер, выполняя задание: С помощью стрелок установить соответствие между понятиями «Отображение плоскости на себя», «Движения», Осевая симметрия», «Центральная симметрия», «Параллельный перенос», «Поворот». Оформить на листах. Отчитаться у доски.

Центральная симметрия.

1. Представим себе, что каждой точке плоскости сопоставляется (ставится в соответствие) какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. Тогда говорят, что дано отображение плоскости на себя. Примером такого отображения является центральная симметрия.

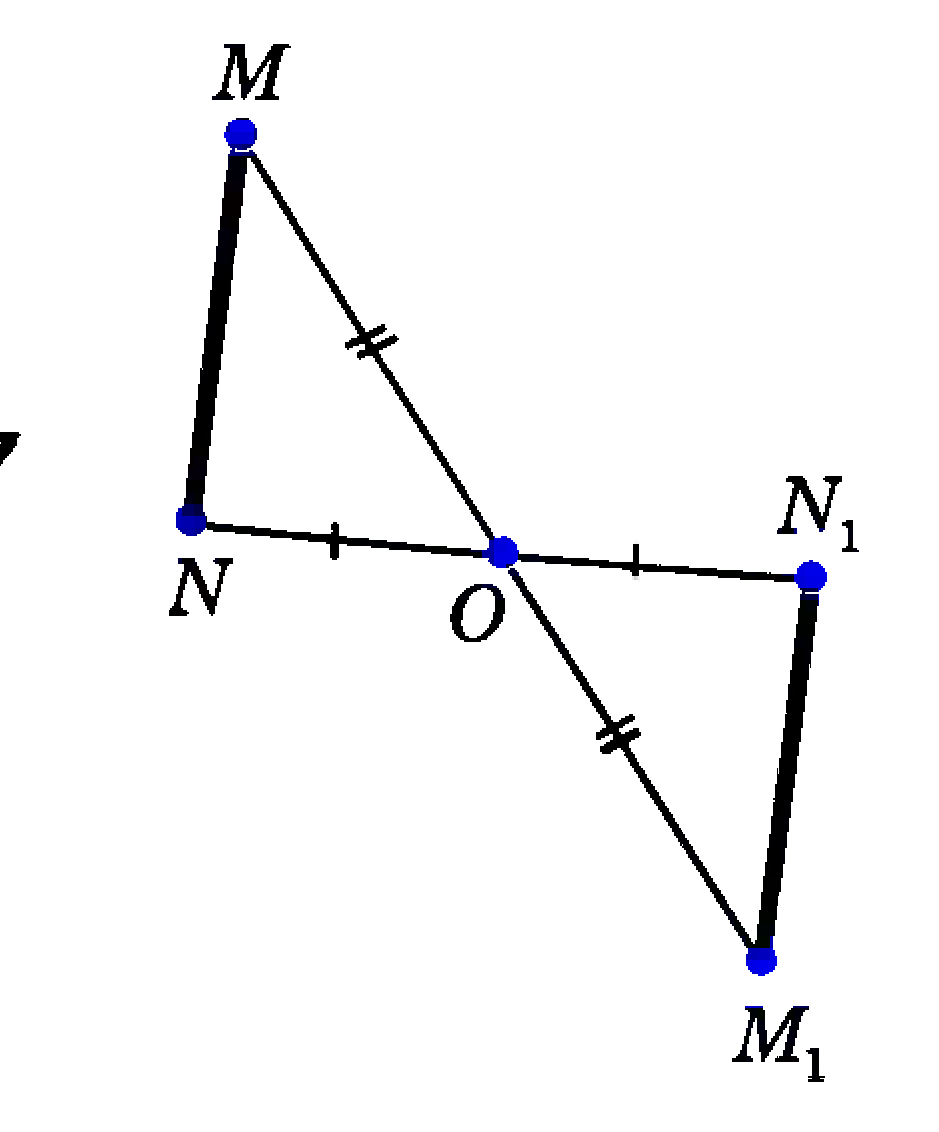
В самом деле пусть точка О - центр симметрии.(см.рис.). Возьмем произвольную точку М, построим симметричную ей точку М₁, относительно точки О. Для этого точку М соединим с точкой О, продлим прямую МО и на продолжении отложим отрезок ОМ₁, равный отрезку ОМ. Мы видим, что с помощью центральной симметрии каждой точке М плоскости сопоставляется точка М₁ этой же плоскости. При этом любая точка М₁ оказывается сопоставленной некоторой точке М. Итак, центральная симметрия представляет собой отображение плоскости на себя.

Задание 1.

Изучи теорию. Запиши в тетрадь определение основных понятий. Выполни построение точки, симметричной данной относительно данной точки О.

Центральная симметрия обладает следующим важным свойством - это отображение плоскости на себя, которое сохраняет расстояния между точками. Любое отображение, обладающее этим свойством, называется движением (или перемещением). Итак, движение плоскости - это отображение плоскости на себя, сохраняющее расстояния.

Задание 2.

Построй в тетради и запиши алгоритм построения отрезка, симметричного данному относительно данной точки.

Построение отрезка, симметричного данному относительно данной точки.

Задание 3.

Построить самостоятельно и обсудить в группе построение треугольника, симметричного данному относительно данной точки.

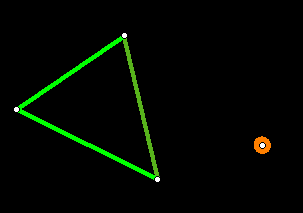
Задание 4.

В экспертной группе выполнить коллективную работу по построению треугольника, симметричного данному, относительно данной точки.

Задание 5.

1) Вернуться в рабочую группу и объяснить одноклассникам свою часть материала. У всех в тетрадях должно быть построено отображение отрезка при всех видах движения.

2) Составить кластер, выполняя задание: С помощью стрелок установить соответствие между понятиями «Отображение плоскости на себя», «Движения», Осевая симметрия», «Центральная симметрия», «Параллельный перенос», «Поворот». Оформить на листах. Отчитаться у доски.

1. Я понял материал своей части 1 2 3 4 5

2. Я активно участвовал в работе группы экспертов 1 2 3 4 5

3. Я понял объяснение одноклассника 1 2 3 4 5

4. Я активно участвовал в составлении кластера

1 2 3 4 5

5. Я не понял или не совсем понял тему:

1) осевая симметрия

2) центральная симметрия

3) параллельный перенос

4) поворот

6. Моя оценка сегодняшнему уроку 1 2 3 4 5

Лист самооценки ученика ____________________

1. Я понял материал своей части 1 2 3 4 5

2. Я активно участвовал в работе группы экспертов 1 2 3 4 5

3. Я понял объяснение одноклассника 1 2 3 4 5

4. Я активно участвовал в составлении кластера

1 2 3 4 5

5. Я не понял или не совсем понял тему:

1) осевая симметрия

2) центральная симметрия

3) параллельный перенос

4) поворот

6. Моя оценка сегодняшнему уроку 1 2 3 4 5

Лист самооценки ученика ____________________

1. Я понял материал своей части 1 2 3 4 5

2. Я активно участвовал в работе группы экспертов 1 2 3 4 5

3. Я понял объяснение одноклассника 1 2 3 4 5

4. Я активно участвовал в составлении кластера

1 2 3 4 5

5. Я не понял или не совсем понял тему:

1) осевая симметрия

2) центральная симметрия

3) параллельный перенос

4) поворот

6. Моя оценка сегодняшнему уроку 1 2 3 4 5

Лист самооценки ученика ____________________

1. Я понял материал своей части 1 2 3 4 5

2. Я активно участвовал в работе группы экспертов 1 2 3 4 5

3. Я понял объяснение одноклассника 1 2 3 4 5

4. Я активно участвовал в составлении кластера

1 2 3 4 5

5. Я не понял или не совсем понял тему:

1) осевая симметрия

2) центральная симметрия

3) параллельный перенос

4) поворот

6. Моя оценка сегодняшнему уроку 1 2 3 4 5

Лист самооценки ученика ____________________

1. Я понял материал своей части 1 2 3 4 5

2. Я активно участвовал в работе группы экспертов 1 2 3 4 5

3. Я понял объяснение одноклассника 1 2 3 4 5

4. Я активно участвовал в составлении кластера

1 2 3 4 5

5. Я не понял или не совсем понял тему:

1) осевая симметрия

2) центральная симметрия

3) параллельный перенос

4) поворот

6. Моя оценка сегодняшнему уроку 1 2 3 4 5

Лист самооценки ученика ____________________

1. Я понял материал своей части 1 2 3 4 5

2. Я активно участвовал в работе группы экспертов 1 2 3 4 5

3. Я понял объяснение одноклассника 1 2 3 4 5

4. Я активно участвовал в составлении кластера

1 2 3 4 5

5. Я не понял или не совсем понял тему:

1) осевая симметрия

2) центральная симметрия

3) параллельный перенос

4) поворот

6. Моя оценка сегодняшнему уроку 1 2 3 4 5