Конспект урока по геометрии для учащихся 7 классов средних общеобразовательных учреждений на тему: «Прямая и отрезок»

Конспект урока по геометрии для учащихся 7 классов средних общеобразовательных учреждений.

Тема урока «Прямая и отрезок» (слайд 1)

Цели урока

Образовательная:

• познакомить учащихся со свойством прямой (через любые две точки можно провести прямую и притом только одну) и научить их использовать его при решении задач.

Задачи:

• систематизация знаний о взаимном расположении точек и прямых.

• ввести для учащихся формулировку свойства прямой

• рассмотреть прием практического проведения прямой на плоскости (провешивание)

• рассмотреть с учащимися пример приводящий к свойству прямой

Развивающая:

- Развитие мышления, развитие навыков исследовательской деятельности.

Воспитательная

-воспитание нравственных качеств личности, аккуратности, добросовестного отношения к работе.

Тип урока: усвоение новых знаний (нестандартный)

Методы обучения: дедуктивно-репродуктивный, индуктивно-репродуктивный.

Требования к знаниям, умениям и навыкам: Учащиеся должны знать взаимное расположение точек и прямых; свойство прямой; прием практического проведения прямых на плоскости (провешивание); решать простейшие задачи по теме.

Оборудование:

• ПК;

• мультимедийный проектор и экран;

• рабочие тетради;

• презентация;

Литература: Геометрия 7-9, Атанасян Л.С., Бутузов В.Ф., Кадомцев С. Б., Поздняк Э. Г., Москва "Просвещение", 2010 год, 384 с. ;

Поурочные разработки по геометрии: 7 класс / Гаврилова Н. Ф. - М: ВАКО, 2005. - 320 с.; Геометрия.

Дидактические материалы. 7 класс / Б. Г. Зив, В. М. Мейлер. 13-е изд. - М: Просвещение, 2010. - 159 с.

План.

1.Организационный момент (2 мин.)

2.Вводная беседа (10 мин.)

3.Изучение нового материала (20 мин.)

4.Закрепление изученного материала (10 мин.)

5.Подведение итогов. Домашнее задание (3 мин.)

Ход урока

1. Организационный момент включает в себя приветствие учителем класса, проверку отсутствующих, готовность помещения к уроку.

2. Учитель: Тема нашего урока «Прямая и отрезок». Запишите тему урока в тетради.

(запись в тетрадях)

Прямая и отрезок

Учитель: Геометрия одна из наиболее древних наук. За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построения прямых углов и т. д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории. (Слайд 2) Название науки «геометрия» древнегреческого происхождения, оно составлено из двух древнегреческих слов «geo»-«земля» и «metreo»- «измеряю» (землю измеряю).(слайд 3)

Появление и развитие геометрических знаний связано с практической деятельностью людей. Это отразилось и в названиях многих геометрических фигур. Термин линия возник от латинского linum - «лен, льняная нить». Практические потребности людей ( сооружение жилищ, желание украшать одежду) способствовали приобретению и накоплению геометрических сведений, которые изначально передавались в устной форме из поколение в поколение. (Слайд 4) Первым ,кто начал получать геометрические факты при помощи рас -суждений (доказательств),был древнегреческий математик Фалес (VI в.до н.э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном языке называется движением.(Слайд 5). Постепенно геометрия становится наукой, в которой большинство фактов устанавливается путем выводов, рассуждений, доказательств. Попытки греческих ученых привести геометрические факты в систему начинаются уже в V веке до н.э. Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III веке до н.э. (Слайд6)

Сочинение Евклида «Начала» почти 2000 лет служило основной книгой , по которой изучали геометрию . В «Началах» были систематизированы известные к тому времени геометрические сведения, и геометрия впервые предстала как математическая наука. Эта книга была переведена на языки многих народов мира , а сама геометрия, изложенная в ней, стала называться евклидовой геометрией. (Слайд 7)

В настоящее время геометрии - это целая наука, занимающаяся изучением форм, размеров, взаимным расположением предметов независимо от их других свойств : массы, цвета и т.д.(Слайд 8)

Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать , делать выводы , то есть логически мыслить. (Слайд 9)

Какие геометрические фигуры вам известны?

Ученик: прямая, отрезок, луч, квадрат, прямоугольник, многоугольник.

Учитель: Правильно. А еще какие фигуры вы знаете?

Ученик: куб, цилиндр, шар, пирамида, параллелепипед.

Учитель: Правильно.

( запись на доске)

Геометрические фигуры

Прямая

Куб

Отрезок

Цилиндр

луч

Шар

прямоугольник

Пирамида

квадрат

Параллелепипед

многоугольник.

Учитель: По какому принципу данные геометрические фигуры записаны в двух различных группах?

Ученик: В первой группе записаны фигуры, существующие на плоскости, а во второй группе - фигуры, существующие в пространстве.

Учитель: Правильно. Часть геометрии, в которой рассматриваются фигуры на плоскости, называется планиметрией, а та часть, в которой рассматриваются фигуры в пространстве, называется стереометрией.

(Слайд 10)

3. Учитель: В курсе математики вы уже знакомы с понятиями прямая, отрезок и многими другими. (Слайд 11)

Начертите прямую. Как ее можно обозначить? (к доске вызывается ученик)

Ученик: Прямая а или AB

(запись на доске и в тетрадях)

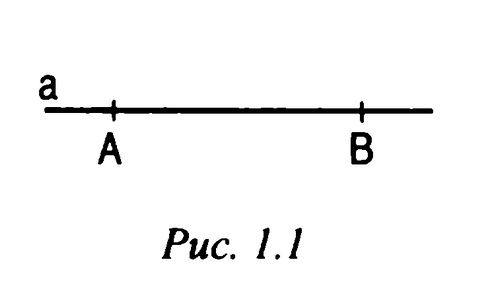
Учитель: Отметьте точку C, не лежащую на данной прямой, и точки D, E, K, лежащие на этой прямой. (к доске вызывается ученик)

Ученик: (запись на доске )

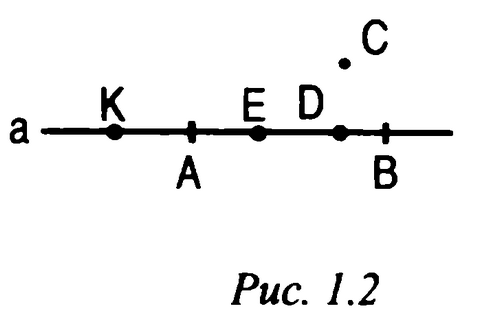
Учитель: Правильно. В математике существуют специальные символы, позволяющие кратко записывать какое - либо утверждение. Символы и означают соответственно «принадлежит» и «не принадлежит» и называются символами принадлежности. Этот знак стал использовать (, от εστι, быть). (Слайд 12)

Ученик:(запись на доске и в тетрадях)

К, E, D a; Ca

Учитель: Использую символы принадлежности, запишите предложение «Точка D принадлежит AB, а точка C не принадлежит прямой а»

(к доске вызывается ученик)

Ученик:

(запись в тетрадях)

Задание: «Точка D принадлежит AB, а точка C не принадлежит прямой а».

(запись на доске и в тетрадях)

DAB, C a.

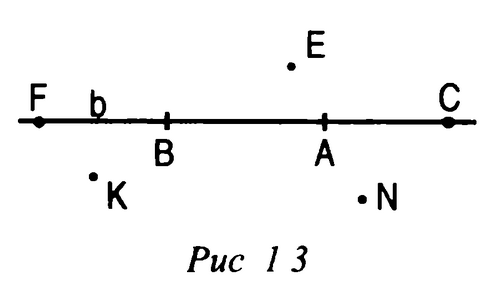
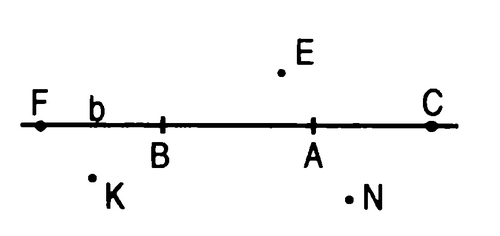
Учитель: Используя рисунок 1.3 (рисунок заранее нарисован на доске )и символы ,, запишите, какие точки принадлежат прямой b, а какие - нет. Рисунок перечертите в тетрадь.

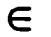
(запись в тетрадях самостоятельно)

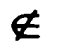
F, B, A, Cb; K, E, Nb

Учитель: Какие точки принадлежат b, и какие не принадлежат?

Ученик: F, B, A, Cb; K, E, Nb

Учитель: Правильно. Сколько прямых можно провести через заданную точку A?

Ученик: Через заданную точку A можно провести множество прямых.

Учитель: Сколько прямых можно провести через две точки?

Ученик: Одну прямую.

Учитель: Через любые две точки можно провести прямую?

Ученик: Да.

Учитель: Итак, через любые две точки можно провести прямую и притом только одну. (Слайд 13)

Это утверждение назовем свойством прямой.

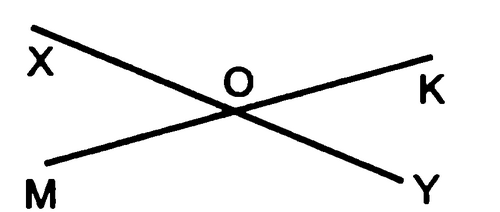
Задание: Начертите прямые XY и MK, пересекающиеся в точке O.

(к доске вызывается ученик)

Ученик: Начертим прямые

(Запись на доске и в тетрадях)

Учитель: Для того, чтобы кратко записать, что прямые XY и MK пересекаются в точке O, используют символ ∩ и записывают так:

(запись на доске и в тетрадях)

XY∩MK=0

Учитель: Этот символ возник в 1888 году. Ввел его Джузе́ппе Пеано (Giuseppe Peano; -) - . Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка . Более всего известен как автор стандартной аксиоматизации натуральной арифметики - . (Слайд 14)

Сколько общих точек может быть у двух прямых?

Ученик: Две прямые могут иметь или одну общую точку или не одной общей точки.

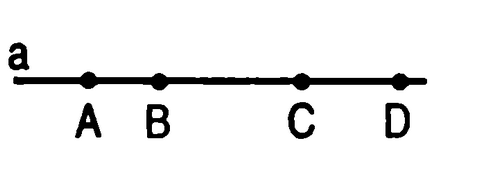
Учитель: Задание 2. На прямой а отметьте последовательно точки A, B, C, D. Запишите все полученные точки. (Слайд 15)

(к доске вызывается ученик)

Ученик: (запись в тетрадях)

Задание 2. На прямой а отметьте последовательно точки A, B, C, D. Запишите все полученные точки.

(запись на доске и в тетрадях)

Задание 2.

Получились отрезки AB, BC, CD, AC, AD, BD.

Учитель: Правильно. Задание 3. Начертите прямые a и b, пересекающиеся в точке M. На прямой a отметьте точку N, отличную от точки M.

а) Являются ли прямые MN и a различными прямыми?

б) Может ли прямая b проходить через точку N? (Слайд 16)

(к доске вызывается ученик)

Ученик: (запись в тетрадях)

Задание 3. Начертите прямые a и b, пересекающиеся в точке M. На прямой a отметьте точку N, отличную от точки M.

а) Являются ли прямые MN и a различными прямыми?

б) Может ли прямая b проходить через точку N?

(запись на доске и в тетрадях)

Задание 3.

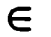
а) Прямая MN и прямая a совпадают, то есть это одна и та же прямая

б) Прямая b не может проходить через точку N.

Учитель: Правильно. Поясните почему?

Ученик: Так как прямая b уже проходит через точку M, а через точки M и N можно провести прямую и притом только одну.

Учитель: Правильно. И это прямая а.

Решим такую задачу: с помощью данной линейки построить отрезок более длинный, чем сама линейка. С этой целью приложим к листу бумаги линейку, я буду делать это на доске, отметим точки A и B b и какую-нибудь точку C, лежащую между A и B.

(Запись на доске и в тетрадях)

Учитель: Затем передвинем линейку вправо так, чтобы ее левый конец оказался около точки C, и отметим точку D около правого конца линейки.

Точки A, B, C и D лежат на одной прямой.

(Запись на доске и в тетрадях)

Учитель: Аналогичный прием используется для «проведения» длинных отрезков на местности. Этот прием заключается в следующем. Сначала отмечают какие-нибудь точки A и B. Для этой цели используют две вехи - шесты длиной около 2 метров, заостренные на одном конце для того, чтобы их можно было воткнуть в землю. Третью веху ставят так, чтобы вехи, стоящие в точках A и B, закрывали ее от наблюдателя, находящегося в точке A. Следующую веху ставят так, чтобы ее закрывали вехи, стоящие в точках B и C, и т.д.

Этот прием называется провешиванием прямой. Он широко используется на практике, например при рубке лесных просек, при прокладывании трассы шоссейной дороги.

4. Учитель: Сейчас выполним на доске и в тетрадях № 2 из учебника.

Задание. Отметьте три точки A, B, C, не лежащие на одной прямой, и проведите прямые AB, BC и CA. (к доске вызывается ученик)

Ученик: (запись на доске и в тетрадях)

№2.

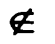
A, B, C не лежат на одной прямой.

AB, BC, CA - прямые.

Учитель: Правильно. Решим следующее задание: №5 Проведите прямую a и отметьте на ней точки A и B. Отметьте: а) точки M и N, лежащие на отрезке AB; б) точки P и Q, лежащие на прямой a, но не лежащие на отрезке AB; в) точки R и S, не лежащие на прямой a. (к доске вызывается ученик)

Ученик: (запись на доске и в тетрадях)

№5.

Учитель: Правильно. Решите следующую задачу.

№ 6. Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой? (к доске вызывается ученик)

Ученик: (запись на доске и в тетрадях)

№6.

Учитель: Правильно. Решим еще одну задачу.

№ 7. Проведите прямую, обозначьте ее буквой a и отметьте точки A и B, лежащие на этой прямой, и точки P, Q и R, не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a, используя символы € и .

(к доске вызывается ученик)

Ученик: (запись на доске и в тетрадях)

№7.

5. Учитель: Итак, урок подходит к концу, давайте подведем итоги. Сформулируйте свойство прямой.

Ученик: через любые две точки можно провести прямую и притом только одну.

Учитель: Правильно. Вы хорошо усвоили материал. Записываем домашнее задание: учебник: §1, вопросы 1-3; Решить задачи: № 3,7.

Дополнительная задача:

Сколько различных прямых можно провести через четыре точки? Рассмотрите все случаи и сделайте рисунки. ( Слайд 17)

Урок окончен. ( Слайд 18)