Урок. Зачет по геометрии по теме Аксиомы. Параллельность прямых и плоскостей

Задание к зачету по теме "Аксиомы. Параллельность прямых и плоскостей"

10-й класс (учебник Л.С. Атанасяна)

1. Знать формулировки:

1. Аксиомы стереометрии (стр. 4 п.2)

2. Следствия из аксиом (стр. 6 п. 3)

3. Определение параллельных прямых в пространстве (стр. 9 п.4)

4. Сформулировать лемму о параллельных прямых (стр.10 п.5)

5. Определение параллельности прямой и плоскости (стр.11 п. 6)

6. Определение скрещивающихся прямых (стр.15 п.7)

7. Алгоритм нахождения угла между скрещивающимися прямыми

8. Угол между прямыми (стр.18 п.9)

9. Определение параллельных прямых (стр.20 п.10)

10. Тетраэдр (стр.24 п.12)

11. Параллелепипед (стр.25 п.13)

2. Уметь доказывать следующие теоремы:

• Признак параллельности прямой и плоскости (стр. 12 п. 6).

• Признак параллельности плоскостей (стр. 20 п. 10).

• Признак скрещивающихся прямых (стр. 15 п. 7).

• Свойства параллельных плоскостей (стр. 21 п. 11).

3. Уметь решать задачи и строить сечение.

Билеты к зачету по теме «Аксиомы. Параллельность прямых и плоскостей.»

Билет 1.

1. Сформулировать аксиомы стереометрии и следствия из аксиом.

2. Доказать признак параллельности прямой и плоскости.

3. Построить сечения:

1. В основании пирамиды SABCD параллелограмм. Провести сечение через ребро AD и точку К ребра SC. Объяснить, какая фигура получилась в сечении.

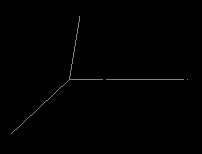
2. Построить сечение AKM. Объяснить, какая фигура получилась в сечении.

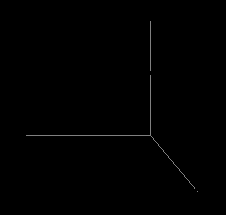
4. Решить задачу: В тетраэдре АВСД K, L, M, N - точки середины ребер АС, ВС, ВД, и АД соответственно. Определите вид четырехугольника KLMN и его периметр, если АВ = 16см и СД = 18см.

Билет 2.

1. Сформулировать определение параллельных прямых в пространстве и лемму о параллельных прямых.

2. Доказать признак параллельности плоскостей.

3. Построить сечения:

1. В основании пирамиды SABCD лежит параллелограмм. Провести сечение через ребро CD и точку N ребра AS. Объяснить, какая фигура получилась в сечении.

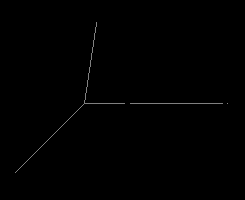
2. Построить сечение, проходящее через точки А, В, С.

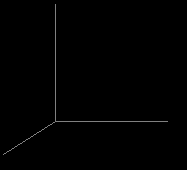
4 Решить задачу: В кубе АВСДА₁В₁С₁Д₁ на ребрах АА₁ и СС₁ выбраны точки M и N так, что AM: MA₁ = 3 : 1 и CN: NC₁ = 1 : 2. Найдите угол между прямыми MN и АС.

</<br>

Билет 3.

1. Сформулировать определение скрещивающихся прямых и алгоритм нахождения угла между скрещивающимися прямыми.

2. Доказать свойства параллельных плоскостей.

3. Построить сечения:

1. Построить сечение тетраэдра плоскостью NKP.

2. Провести сечение , где К - середина ребра АВ. Объяснить, какая фигура получилась в сечении.

4. Решить задачу: Через точку О, расположенную между параллельными плоскостями α и β, проведены три прямые, которые пересекают эти плоскости в точках А, А₁; В, В₁ и С, С₁ соответственно. Найдите сторо15см.ны треугольника А₁В₁С_1, если его площадь равна 21 см² и АВ = 13см, ВС = 14см, АС =15см.

Билет 4.

1. Рассказать о тетраэдре.

2. Доказать свойства параллельных плоскостей.

3. Построить сечения:

1. Построить сечение, проходящее через точку К параллельно ребрам АВ и DC.

2. Построить сечение плоскостью NMP

4. Решить задачу: Параллельные прямые АС и ВД пересекают плоскость α в точках А и В. Точки С и Д лежат по одну сторону от плоскости α, АС =8см, ВД = 6см, АВ = 4см. Докажите, что прямая СД пересекает плоскость α в некоторой точке Е. Вычислите длину отрезка ВЕ.