Конспект урока по теме Преобразование графиков функций

Предмет:Алгебра

Класс: 10 класс

Тема урока: "Преобразование графиков функции у = sin x»

Цель занятия: показать применение преобразований графиков при решении уравнений и неравенств.

Развивающие цели: развитие внимания и наблюдательности, навыков исследования, грамотной математической речи,

Воспитательные цели: воспитывать умение работать в необычной ситуации.

Методы обучения:

• частично-поисковый,

• объяснительно-иллюстративный,

• исследовательский метод,

Формы организации урока: индивидуальная, фронтальная, работа в группах, защита проектов

Оборудование урока

Компьютер, мультимедийный проектор, экран, программное обеспечение Microsoft Office, мультимедийная презентация к уроку, ручки, листы бумаги, пакеты с раздаточным материалом, буклеты «ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ФУНКЦИЙ».

Условия достижения результатов:

1. взаимосвязь тригонометрии с другими науками;

2. соблюдение преемственного обучения;

3. опора на полученные ранее знания;

4. активное взаимодействие учащихся в классе.

Основные принципы проведения урока:

1. наглядность;

2. доступность;

3. систематичность;

4. связь с предыдущим (непрерывность).

Ход занятия.

1.Сообщение темы и постановка целей урока.

Посмотрите, пожалуйста , на слайд. Как вы думаете, что позволило мне соединить эти изображения и звуковое оформление на одном слайде? ( во всех этих изображениях мы встретимся с функцией у= sin x( работа генератора в автомобиле, поступление газа в газовом котле, закат солнца . и музыку, которую вы услышали , исполненную на новом музыкальном инструменте, который называют терменвокс, можно записать только при помощи синусоид.

На прошлом уроке мы познакомились с функцией у= sin x, её свойствами и графиком. Узнали, что график называют синусоидой. Но к сожалению, в чистом виде тригонометрические функции встречаются не так часто. Гораздо чаще приходится иметь дело с функциями, полученными из основных элементарных при помощи добавления констант и коэффициентов. Графики таких функций можно строить, применяя геометрические преобразования к графикам соответствующих основных тригонометрических функций (или переходить к новой системе координат). Сегодня на уроке мы рассмотрим только два преобразования -параллельный перенос вдоль оси абсцисс и вдоль оси ординат

Итак, цель нашего урока рассмотреть применение преобразований графиков функции y=sin x для решения уравнений и неравенств

2. математический диктант2. Не выполняя построения, определите, принадлежит ли графику функции точка: .

.

Я прошу вас поменяться тетрадями и оценить работу вашего одноклассника, по критериям приведенным на доске.

3. Изучение нового материала

Алгоритмы построения этих графиков вам знакомы. Повторим.

• График функции y=f(x+a) можно получить, выполнив параллельный перенос вдоль оси Ох на а единичных отрезков вправо, если а<0 и на а единичных отрезков влево, если а>0.

• График функции y=f(x)+a можно получить, выполнив параллельный перенос вдоль оси Оy на а единичных отрезков вниз, если а<0 и на а единичных отрезков вверх, если а>0.

• Задание 1. Построить график функции y=sin(х - 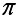). Строим систему координат. Делаем разметку...

Как выполнить построение графика функции y=sin(х - )?...

"Зацепились" за макушку волны, например, точку (/2; 1), переместили шаблон на 6 клеток вправо. Подписали график. А теперь посмотрим, как изменились свойства функции.

На доске оформлена таблица свойств функции y=sinx. Задание: рассказать о свойствах функции y=sin(х-). К экрану приглашаю ученика "прочитать" свойства. Ученик работает с указкой, а сама записываю на доске свойства функции, заполняя правую часть таблицы. Если свойство не изменилось, то для экономии времени просто ставлю знак "+".

f - возр. на

[-/2+2n; /2+ 2n]

f - возр. на

[/2+2n; 3/2+ 2n]

f - убыв.на

[/2+2n; 3/2+ 2n]

f - убыв.на

[-/2+2n; /2+ 2n]

yнаиб. = 1,

при х=/2 + 2n

не изменилось

при х= -/2 + 2n

yнаим. = - 1,

при х= -/2 + 2n

не изменилось

при х= /2 + 2n

у=0, при х=n

не изменилось

Какое преобразование надо выполнить и что произойдет с данным графиком? Проверим вашу гипотезу... (показываю анимацию параллельного переноса на 2). Почему же при этом преобразовании графики полностью совместились? Приведите свои примеры таких функций?

Работа в группах: построить графики функций и описать их свойства:,.,

y=sin (x- y=sin (x+ y=sin (x- y=sin (x- y=sin (x+

Обобщить преобразования графиков функций сдвигом по оси .

Задание 3В одной системе координат построить графики функций одной группы и описать их свойства:

1) , , , , f - возр. на

[- π/2+2πn; π/2+ 2πn]

f - возр. на

[- π/2+2πn; π/2+ 2πn]

f - убыв.на

[π/2+2πn; 3π/2+ 2πn]

f - убыв.на

π/2+2πn; 3π/2+ 2πn]

yнаиб. = 1,

при х= π/2 + 2πn

yнаиб. = 3,

при х= π/2 + 2πn

yнаим. = - 1,

при х= - π/2 + 2πn

yнаим. = 1,

при х= -π/2 + 2πn

у=0, при х=πn

нет

Обобщить преобразования графиков функций сдвигом по оси .

Задания 4 . построим график функции .

При решении каких заданий нам будут необходимы умения строить графики? ...

Конечно, при решении уравнений и неравенств графическим способом.

Задания 6, 7 и 8 решаем устно с комментированием.



Задание 9. Решаем в тетради, комментируя шаги построения каждого графика. Ответ: корней нет.

Проверочная работа.

Для учащихся группы A:Для учащихся группы Б:

Задание 10. Решить самостоятельно, с последующей проверкой.

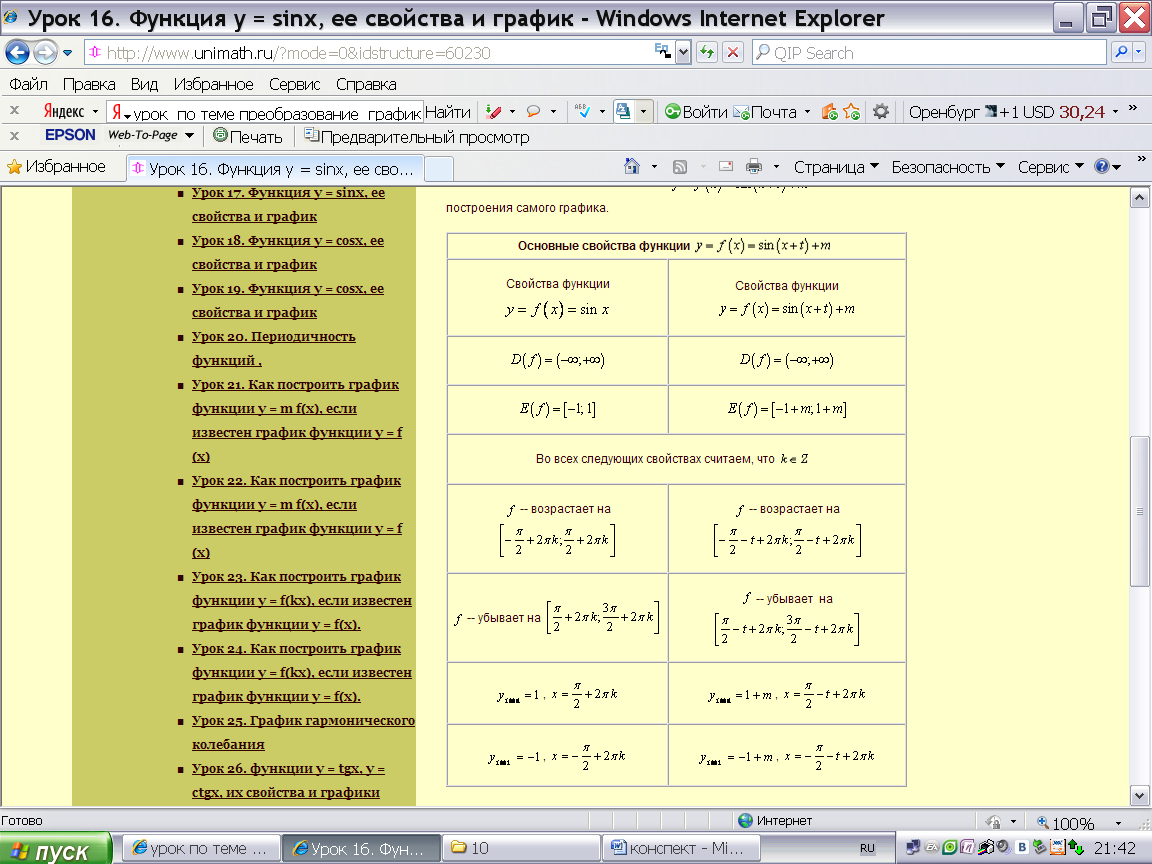
Задание 11. Решить неравенство самостоятельно, с последующей проверкой. Здесь я предлагаю детям найти различные формы записи ответа к заданию. Например, х(-3/2+2n; -5/6+ 2n) или х(/2+2n; 7/6+ 2n), nZ.

Задание 12. Устно.

Подведем итоги. При решении каких заданий нам потребуется построение графиков? Слайд 14.

5. практическая работа(или домашнее задание)

Пристыковка плит керамогранита разного цвета - это модная ныне тенденция в дизайне при напольной укладке природного или искуственного камня. Плавные линии в виде синусоид, которые образуются при соприкосновении контрастных по цвету плит, стабильно производят эффект дороговизны отделки и сложности выполненых работ. Не говоря уже о том, что это действительно красиво. Волнообразная резка керамогранита осуществляется с помощью технологии гидроабразивной резки согласно дизайнерского проекта, который в электронном виде становится программой для станков с ЧПУ. Попробуйте себя в роли дизайнера. Составьте свой узор для укладки плитки.

6. Итог урока

Исследователь Д. Азаров также уверен, что Земля живая и разумная. Более того, он утверждает, что странные рисунки в пустыне Наска, которые можно охватить взглядом только с самолета, надпись на хлебном поле в графстве Гемпшир, странные круги и каменные спирали сделаны нашей разумной планетой...

Кстати, изображений птиц и животных на плато Наска не так уж много - всего 30 рисунков. Остальное - синусоиды, всего более 13 тысяч узоров на площади около 500 квадратных километров. Специалисты подсчитали, что для того, чтобы вручную создать это "полотно", древним художникам потребовалось бы не менее ста тысяч человеко-лет... Удивительна и сверхвысокая точность, присущая загадочным рисункам. Так что же такое синусоида-наше прошлое, настоящее или будущее?