Методическая разработка по теме Приложения производной

</ Министерство образования и науки РФ

ГБПОУ ВО «Воронежский техникум строительных технологий»

МЕТОДИЧЕСКОЕ ПОСОБИЕ

по дисциплине МАТЕМАТИКА

Приложения производной

Воронеж

2016

Рассмотрено на заседании ПЦК математических дисциплин

Протокол № _____ от _____________

Председатель ПЦК _______ Болычева Т.В.

Разработана на основе Федерального государственного образовательного стандарта среднего профессионального образования для всех специальностей 1 курса

Автор-составитель: Сафонова Елена Артуровна, преподаватель ГБПОУ «Воронежский техникум строительных технологий»

Настоящее пособие предназначено для студентов 1 курса всех специальностей и полностью соответствует программе по математике для СПО. Оно может быть использовано студентами для самостоятельного изучения раздела программы, а также преподавателем на уроке при изучении нового материала, для домашнего задания, при повторении и подготовке к контрольной работе.

Пособие включает в себя, помимо задач, краткие теоретические сведения и формулы, необходимые для решения задач указанного раздела математического анализа, подробные решения типовых примеров и задач, вопросы для самопроверки, а также упражнения для самостоятельного решения и примерный вариант контрольной работы по теме.

СОДЕРЖАНИЕ

1. Введение…………………………………………………………………………………….4

2. Физический и механический смысл производной. Понятие о второй производной…5

3. Применение производной к решению прикладных задач………………………………..7

4. Понятие касательной и нормали. Геометрический смысл производной………………..8

5. Исследование функции на монотонность с помощью производной…………………...10

6. Исследование функции на экстремум по первой и второй производной………………14

7. Применение производной для построения графика……………………………………...18

8. Построение графика квадратного трёхчлена……………………………………………. .20

9. Наибольшее и наименьшее значения функции на отрезке…………………………….....22

10. Примерный вариант контрольной работы……………………………………………….24

11. Литература………………………………………………………………………………….25

Введение

В Концепции модернизации Российского образования подчеркивается: «Развивающемуся обществу нужны современно образованные, нравственные, предприимчивые люди, которые могут самостоятельно принимать ответственные решения в ситуации выбора, прогнозируя их возможные последствия, способные к сотрудничеству, отличаются мобильностью, динамизмом, конструктивностью, развитым чувством ответственности за судьбу страны».

Математика является фундаментальной общеобразовательной дисциплиной со сложившимся устойчивым содержанием и общими требованиями к подготовке обучающихся. В учреждениях СПО выбор целей смещается в практическом направлении, предусматривающем усиление и расширение прикладного характера изучения математики; преимущественной ориентации на алгоритмический стиль познавательной деятельности.

Раздел математики «Математический анализ» является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры современного специалиста. Этот раздел является базовым в математическом анализе, а изучение приложений производной позволяет студентам осмыслить возможность решения широкого спектра практических задач. Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке специалиста, выработку представления о роли и месте математики в современной цивилизации и в мировой культуре, умение логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений.

С введением Федеральных государственных образовательных стандартов профессионального образования нового поколения меняется подход к преподаванию дисциплин общеобразовательного цикла, который предусматривает формирование новых ключевых компетенций, необходимых для современного специалиста, таких как экономическая (ориентация в современной рыночной экономике, участие в ней не только в качестве объекта - потребителя, но и субъекта - предпринимателя, менеджера, производителя товаров и услуг и т.д.) и профессиональная (ориентированность в профессии, профессиональная подготовка к выполнению в будущем социальных ролей «специалиста», «профессионала»).

ФИЗИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ.

ПОНЯТИЕ ВТОРОЙ ПРОИЗВОДНОЙ

В конце семнадцатого века великий английский ученый Исаак Ньютон открыл общий способ описания связи между путем и скоростью движения. Основными математическими понятиями, выражающими эту связь, являются производная и скорость. Честь открытия основных законов математического анализа также принадлежит великому немецкому математику Готфриду Лейбницу.

1. Физический смысл первой производной

Производная y функции - это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём и временем при прямолинейном неравномерном движении выражается уравнением , то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени нужно найти производную и подставить в неё соответствующее значение , то есть

П р и м е р 1. Точка движется прямолинейно по закону (s выражается в метрах, t - в секундах). Найти скорость движения через 3 секунды после начала движения.

Решение. Скорость прямолинейного движения равна производной пути по времени, то есть .

Подставив в уравнение скорости с, получим

П р и м е р 2. Маховик, задерживаемый тормозом, поворачивается за t с на угол

(t) = 4t - 0,2t² (рад). Найдите:

а) угловую скорость вращения маховика в момент t = 6 с;

б) в какой момент времени маховик остановится?

Решение. а) Угловая скорость вращения маховика определяется по формуле Тогда

Подставляя t = 6 с, получим .

б) В тот момент, когда маховик остановится, его скорость будет равна нулю . Поэтому . Отсюда

П р и м е р 3. Тело массой 6 кг движется прямолинейно по закону Найти кинетическую энергию тела через 3 с после начала движения.

Решение. Найдём скорость движения тела в любой момент времени t.

Вычислим скорость тела в момент времени .

Определим кинетическую энергию тела в момент времени

2. Производная второго порядка. Производная n-го порядка.

Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.

Производная от производной называется второй производной или производной второго порядка и обозначается .

Производная от второй производной называется производной третьего порядка и обозначается Производной n-го порядка называется производная от производной порядка и обозначают или

Примеры.

1) 2)

.

3. Механический смысл второй производной.

Если первая производная функции - это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная - это скорость изменения скорости или ускорение, то есть

Итак, первая производная - это скорость изменения процесса, вторая производная - ускорение.

П р и м е р 4. Точка движется прямолинейно по закону . Найти скорость и ускорение точки в момент .

Решение. Найдём скорость точки в любой момент времени t.

Вычислим скорость в момент времени .

Найдём ускорение точки в любой момент времени t.

и , то есть ускорение в этом случае является величиной постоянной.

П р и м е р 5. Тело массой 3 кг движется прямолинейно по закону +5. Найти силу, действующую на тело в момент времени

Решение. Сила, действующая на тело, находится по формуле

Найдём скорость движения точки в любой момент времени t.

.

Тогда .

Найдём ускорение: =

Тогда .

Вопросы для самопроверки

1. В чём заключается физический смысл первой производной?

2. Как найти мгновенную скорость прямолинейного неравномерного движения? Запишите формулу.

3. Что называется производной второго порядка, третьего порядка, n-го порядка?

4. В чём заключается механический смысл производной?

5. Как найти ускорение прямолинейного неравномерного движения в данный момент времени? Запишите формулу.

ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К РЕШЕНИЮ

ПРИКЛАДНЫХ ЗАДАЧ

Решите задачи.

1. Путь, пройденный материальной точкой, задаётся уравнением

. Найти скорость и ускорение точки в конце 5-й секунды.

2. Вычислить ускорение материальной точки в конце 3-й секунды, если точка движется по закону .

3. Точка движется прямолинейно по закону . Найти скорость и ускорение точки в момент секунды.

4. Материальная точка движется прямолинейно по закону . Найти её ускорение в конце 3-й секунды.

5. Путь, пройденный клетью подъёмной машины, определяется уравнением

. Найти скорость и ускорение в момент времени 5 с.

6. Определить момент , в который ускорение прямолинейного движения, совершаемого по закону , равно нулю. Какова при этом скорость?

7. Закон движения частицы определяется уравнением . Каково ускорение частицы в момент, когда её скорость равна 11 м/с?

8. Температура тела T изменяется в зависимости от времени t по закону

. С какой скоростью нагревается это тело в момент времени ?

9. Количество электричества, протекающего через проводник, задаётся формулой . Найти силу тока в конце 4-й секунды.

10. Сила тока изменяется в зависимости от времени по закону (I - в амперах, t - в секундах). Найти скорость изменения силы тока в конце 8-й секунды.

11. Известно, что тело массой m = 5кг движется прямолинейно по закону . Найдите кинетическую энергию тела через 2с после начала движения.

12. Две материальные точки движутся прямолинейно по законам: В какой момент времени скорости их равны?

13. Две материальные точки движутся прямолинейно по законам: В какой момент времени скорость первой точки будет в два раза больше скорости второй?

14. Основание а параллелограмма изменяется по закону , а высота по закону Вычислите скорость изменения его площади в момент t = 4c. (Основание а и высота b измеряются в сантиметрах).

15. Радиус круга R изменяется по закону . C какой скоростью изменяется его площадь в момент , если радиус круга измеряется в сантиметрах.

16. Материальная точка массой 2кг движется прямолинейно по закону

, где s- путь в метрах, t - время в секундах. Найдите силу, действующую на неё в момент t = 3 c.

17. Маховик, задерживаемый тормозом, поворачивается за t секунд на

угол (t) = (рад). Найдите:

а) угловую скорость вращения маховика в момент t = 6с;

б) в какой момент маховик остановится?

18. Материальная точка движется прямолинейно по закону ,

где s - путь в метрах, t - время в секундах. Найдите:

а) момент времени t, когда ускорение точки равно 0;

б) скорость, с которой движется точка в этот момент времени.

ПОНЯТИЕ КАСАТЕЛЬНОЙ И НОРМАЛИ.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

1. Понятие касательной и нормали к кривой

Мы знаем аналитический и физический смысл производной:

аналитический смысл - это , физический - это скорость процесса, заданного функцией. Выясним геометрический смысл производной.

Для этого введём понятие касательной к кривой в данной точке.

Из школьного курса геометрии, вы знаете понятие касательной к окружности. Касательная к окружности определяется как прямая, лежащая в одной плоскости с окружностью и имеющая с ней единственную общую точку.

Но такое определение касательной неприменимо для случая произвольной кривой. Например, для параболы оси имеют по одной общей точке с параболой. Однако ось является касательной к параболе, а ось - нет.

M₁ Дадим общее определение касательной к

L M₂ кривой в данной точке.

М₃ Пусть - некоторые точки произвольной кривой - секущая кривой.

K При приближении точки по кривой секущая будет поворачиваться вокруг точки , занимая положения ,

Рис.1

Определение. Предельное положение секущей при неограниченном приближении точки по кривой называется касательной к кривой в точке

Определение. Нормалью к кривой в точке называется прямая, проходящая через точку перпендикулярно касательной к кривой в этой точке.

Если - касательная к кривой в точке ,

то перпендикулярная будет нормалью к кривой в точке

Рис.2

2. Геометрический смысл производной

Пусть кривая является графиком функции . Точки

лежат на графике функции. Прямая - секущая кривой . - касательная к кривой

- угол наклона касательной

0 Рис.3

Геометрически, производная функции в точке равна тангенсу угла наклона касательной, проведённой в точке или угловому коэффициенту касательной к графику функции в этой точке.

Уравнение касательной к кривой в точке имеет вид

Уравнение нормали к кривой в точке имеет вид

РЕШЕНИЕ ЗАДАЧ

П р и м е р 1. Вычислите угловые коэффициенты касательных к параболе в точках .

Решение. Из геометрического смысла производной (формула 1) угловой коэффициент касательной .

Найдём производную функции: .

1. Найдём значение производной в точке

. Следовательно, .

2. Найдём значение производной в точке

. Следовательно, .

П р и м е р 2. У параболы проведены касательные в точках Найдите углы наклона касательных к оси Ох.

Решение. По формуле (1)

Найдём . .

1. Вычислим значение производной в точке : .

Следовательно, и .

2. Аналогично в точке .

Следовательно, и

П р и м е р 3. В какой точке касательная к кривой наклонена к оси Ох

под углом

Решение. По формуле (1)

; . Следовательно, и

Подставив в функцию , получим . Получили точку .

П р и м е р 4. Составить уравнение касательной и нормали к параболе в точке

Решение. Уравнение касательной к кривой имеет вид .

Из условия задачи . Найдём производную .

; .

Подставив все значения в уравнение получим уравнение касательной

или .

Составим уравнение нормали, воспользовавшись формулой :

или

Вопросы для самопроверки

1. Дайте определение касательной к кривой.

2. Что называется нормалью к кривой?

3. В чём заключается геометрический смысл производной? Запишите формулу.

4. Запишите уравнение касательной к кривой в данной точке.

5. Запишите уравнение нормали к кривой в данной точке.

УПРАЖНЕНИЯ

1. Найти угловой коэффициент касательной, проведённой к кривой

в точке .

2. Кривая задана уравнением Определить углы наклона касательных к положительному направлению оси , проведённых к кривой в точках

с абсциссами .

3. В какой точке касательная к кривой : а) параллельна оси ; б) образует с осью угол 45?

4. В какой точке касательная к графику функции параллельна оси абсцисс?

5. Найти угол наклона касательной к кривой в точке, абсцисса которой равна 2.

6. Составить уравнение касательной к кривой в точке .

7. Найти касательную к кривой в точке с абсциссой .

Задачи для самостоятельного решения

8. Найти абсциссу точки параболы , в которой касательная параллельна оси абсцисс.

9. Найти угловой коэффициент касательной, проведённой к кривой

в точке .

10. В какой точке касательная к кривой образует с осью угол 30?

11. Составить уравнение касательной к параболе в точке с абсциссой

12. Составить уравнение касательной к гиперболе в точке

13. В каких точках угловой коэффициент касательной к кубической параболе равен 3?

14. Составить уравнение касательной к параболе в точке с абсциссой .

15. Составить уравнение касательной к кривой в точке с абсциссой

16. Составить уравнение касательной к кривой в точке с абсциссой

17. Какой угол образует с осью абсцисс касательная к параболе , проведённая в точке M ? Составить уравнение этой касательной.

18. Найти координаты точки, в которой касательная к параболе образует с осью угол в 135.

19. На кривой найти точку, в которой касательная параллельна прямой .

20. В какой точке касательная к графику функции образует угол 135

с осью ?

ИССЛЕДОВАНИЕ ФУНКЦИИ НА МОНОТОННОСТЬ С ПОМОЩЬЮ ПРОИЗВОДНОЙ

Рассмотрим приложение производной к исследованию функции на возрастание и убывание.

1. Признаки возрастания и убывания функции.

Теорема 1 (признак возрастания функции). Если дифференцируемая функция

возрастает на данном интервале, то производная этой функции не отрицательна на этом интервале.

Теорема 2 (признак убывания функции). Если дифференцируемая функция

убывает на данном интервале, то производная этой функции не положительна на этом интервале.

Обратные теоремы также справедливы.

Теорема 3 (признак возрастания функции). Если производная функции

положительна на некотором интервале, то функция на этом интервале монотонно возрастает.

Теорема 4 (признак убывания функции). Если производная функции

отрицательна на некотором интервале, то функция на этом интервале монотонно убывает.

Эти утверждения можно пояснить геометрически.

Рис.4 Рис.5

Если функция возрастает, то и , а это возможно только при

. Следовательно, угол наклона касательной - острый.

Если функция убывает, то и

, а это возможно только при . Следовательно, угол наклона касательной - тупой.

Такие рассуждения приводят к выводу: на промежутке монотонности (возрастания или убывания) производная свой знак не меняет.

Изменение характера монотонности происходит при изменении знака производной . А это возможно лишь при переход производной через ноль или через точку, в которой производная не существует (точка .

Рис.6

Из этих рассуждений следует правило нахождения промежутков монотонности.

2. Правило исследования функции на монотонность

1. Найти производную функции .

2. Найти точки, в которых производная или не существует.

Эти точки называются критическими точками для функции

3. Отметить критические точки на числовой прямой и определить знак производной в каждом из полученных интервалов, входящих в область определения функции.

4. По полученным знакам производной сделать вывод о характере монотонности: если , то функция возрастает;

если , то функция убывает.

П р и м е р. Найти промежутки монотонности функции .

Решение. 1) Найдём производную функции

2) Найдём критические точки

, если 3 или (разделили на 3).

Решив уравнение, получим и .

3) Отметим критические точки на числовой прямой и определим знак производной

-1 2

3. Вывод: функция возрастает при

функция убывает при

Вопросы для самопроверки

1. Сформулируйте признак (прямой и обратный) возрастания функции.

2. Сформулируйте признак (прямой и обратный) убывания функции.

3. Как связаны монотонность функции и угол наклона касательной к графику этой функции?

4. Какие точки называются критическими для функции?

5. Сформулируйте правило исследования функции на монотонность.

Упражнения

Исследовать функции на монотонность:

1. 2.

1. 3. 4.

2. 5. ; 6.

3. ИССЛЕДОВАНИЕ ФУНКЦИИ НА ЭКСТРЕМУМ ПО ПЕРВОЙ И ВТОРОЙ ПРОИЗВОДНОЙ

1. Определение точек экстремума.

4. Рассмотрим график функции , изображённый на рисунке.

5. 

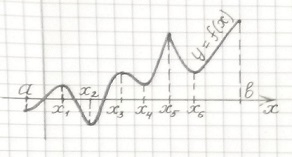
6. Рис.7

7. В точках функция переходит от возрастания к убыванию и в этих точках функция принимает наибольшие значения по сравнению с рядом лежащими точками.

8. В точках функция переходит от убывания к возрастанию и в этих точках функция принимает наименьшие значения по сравнению с рядом лежащими точками.

9. Вот такие точки функции и называются точками максимума и минимума.

10. Определение 1. Точка называется точкой максимума функции , если для всех взятых из некоторой окрестности точки , выполняется условие

11. Определение 2. Точка называется точкой минимума функции , если для всех взятых из некоторой окрестности точки , выполняется условие

12. Значения функции в точках максимума и минимума называются соответственно максимумом и минимумом функции.

13. Максимум и минимум функции объединяют названием экстремумы функции. Точки максимума и минимума называются точками экстремума (или экстремальными точками).

19. Рис.8

22. функции

23. Надо отметить, что максимум функции не всегда является наибольшим значением во всей области определения функции, он является наибольшим лишь по сравнению со значениями функции, взятыми в некоторой окрестности этой точки.

24. 2. Признаки существования точек экстремума.

25. В точках экстремума функция должна переходить от возрастания к убыванию или от убывания к возрастанию. А это значит, что производная при переходе через эту точку должна поменять свой знак. Это возможно только при переходе производной через ноль или через точку, в которой производная не существует.

26. Вывод: если или не существует, то функция в точке может иметь экстремум.

28. Это условие, являясь необходимым, не является достаточным. Например, для функции точка не является точкой экстремума, хотя производная в этой точке

29. Почему? Потому что производная при переходе через эту точку должна поменять свой знак, а у нас функция остаётся возрастающей и производная знак не меняет.

38. Рис. 9

39. Итак, получаем теорему, в которой сформулированы необходимое и достаточное условия существования точек экстремума.

40. Теорема 5. Чтобы точка , была точкой экстремума функции , необходимо и достаточно, чтобы

41. а) или не существовала,

42. б) при переходе через точку производная должна менять свой знак.

43. Эта теорема даёт правило нахождения точек экстремума.

46. 3. Правило исследования функции на экстремум.

1. Найти производную функции .

2. Найти критические точки функции, т.е. значения аргумента , при которых производная или не существует.

3. Определить знак производной , в окрестности критических точек

47. а) Если при переходе через точку меняет знак с «+» на « - », то - точка максимума;

48. б) если меняет знак с « - » на «+», то - точка минимума;

49. в) если знак не меняет, то точкой экстремума не является.

50. 4. Вычислить значения функции в точках экстремума и .

51. 5. При необходимости построить схематически график.

52. П р и м е р. Исследовать функцию на экстремум и построить схематически график.

54. Решение. 1. Найдём производную функции: .

2. Найдём критические точки:

55. , если или .

56. или

3. Отметим полученные значения на числовой прямой и определим знак производной в каждом из полученных интервалов.

60. + - +

4. Вычислим значения функции в точках экстремума.

62. . Получаем точку .

63. . Получили точку .

5. По полученным точкам строим график.

4. Второе правило исследования функции на экстремум.

73. Часто бывает рациональнее исследовать функцию на экстремум с помощью второй производной. Рассмотрим сущность этого метода.

74. Знак первой производной данной функции характеризует возрастание и убывание функции. Точно так же знак второй производной характеризует возрастание и убывание первой производной.

75. Теперь выясним, как изменяется первая производная в точках экстремума и близких к ним точках с увеличением аргумента. Первая производная при переходе через точку максимума меняет знак с «+» на «-». Иными словами, она от положительных значений переходит через ноль к отрицательным, т. е. убывает, а значит, её производная должна быть отрицательна. Итак, в точке максимума данной функции первая производная равна нулю, а вторая производная отрицательна.

76. Аналогично можно показать, что в точке минимума функции первая производная равна нулю, а вторая отрицательна.

77. Отсюда вытекает правило исследования функции на экстремум с помощью второй производной.

1. Найти первую производную .

2. Найти критические точки, т.е. точки, в которых

3. Найти вторую производную .

4. Во вторую производную подставить поочерёдно все критические значения

78. ;

79. если то - точка минимума,

80. если то - точка максимума,

81. если то следует обратиться к первому правилу.

5. Вычислить значения функции в точках экстремума и построить схематически график.

82. П р и м е р. Исследовать функцию на экстремум по второму правилу

84. Решение. 1. Найдём первую производную

85. 2. Найдём критические точки

86. , если ,

88. ,

89. .

90. 3. Найдём вторую производную

91. .

92. 4. Определим знак второй производной в каждой критической точке.

93. , значит - точка максимума,

94. , значит - точка минимума,

95. , значит

96. 5. Вычислим значения функции в точках экстремума.

97. Точка

98. . Точка .

99. Точка

100. Построим схематически график.

101. y

103. - x

111. Вопросы для самопроверки

112. 1. Что называется точкой максимума функции? Проиллюстрируйте на рисунке.

113. 2. Что называется точкой минимума функции? Покажите, как это выглядит на рисунке.

114. 3. Что такое максимум и минимум функции?

115. 4. Сформулируйте необходимое и достаточное условия существования точек экстремума.

116. 5. Перечислите порядок нахождения точек экстремума по первой производной.

117. 6. Как исследовать функцию на экстремум по второй производной?

131. УПРАЖНЕНИЯ

133. 1. Исследуйте функции на монотонность и точки экстремума. Постройте график.

2. 2.

3. 3.

4. 4.

6. 5.

7. 6. ;

8. 7.

9. 8.

10. 9.

11. 2. Исследуйте функцию на экстремум по второму правилу.

12. 1.

13. 2.

14. 3. ;

15. 4.

16. Задания для самостоятельного решения

17. 1. Исследуйте функцию на монотонность и точки экстремума по первому правилу.

18. 1. ;

19. 2. ;

20. 3.

21. 4. ;

22. 5. ;

23. 6.

24. 7.;

25. 8.

26. 2. Исследуйте функцию на экстремум по второму правилу.

27. 1.

28. 2.

29. 3. ;

30. 5. .

52. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ

53. НА МОНОТОННОСТЬ И ЭКСТРЕМУМЫ

55. 1. Исследовать функцию на монотонность и точки экстремума.

56. 1.

57. 2.

58. 3.

59. 4.

60. 5.

61. 6.

62. 7.

63. 8.

64. 2. Исследовать функцию на экстремум и постройте схематически график:

65. 1.

66. 2.

67. 3.

68. 4.

69. 5.

70. 6.

71. 7. ;

74. 8.

75. 9.

76. 10.

77. 11.

78. 12.

79. 13.

80. 14.

81. 3. Исследовать функцию на экстремум по второй производной и построить схематически график:

82. 1.

83. 2.

84. 3.

85. 4.

86. 5.

102. ПОСТРОЕНИЕ ГРАФИКА КВАДРАТНОГО ТРЁХЧЛЕНА

103. Как известно, функция , где , называется квадратичной, а многочлен , часто называют квадратным трёхчленом. Рассмотрим построение графика квадратного трёхчлена.

104. 1. Найдём вершину параболы. Её можно найти двумя способами.

105. 1) Из школьного курса известно, что абсцисса вершины параболы находится по формуле . Чтобы найти ординату нужно в функцию вместо х подставить найденное значение абсциссы .

106. 2) Для квадратичной функции вершина параболы является точкой экстремума. Причём если то ветви параболы направлены вверх и вершина параболы является точкой минимума. При этом возможно 3 случая, связанные со знаком дискриминанта.

112. Рис.10

113. Если , то ветви параболы направлены вниз и её вершина является точкой максимума. При этом возможно 3 случая.

120. Рис.11

121. Поэтому, чтобы найти абсциссу вершины параболы нужно найти производную и приравнять её к нулю.

122. Иногда для более точного построения графика необходимо найти точки пересечения графика с осями координат.

123. Точки пересечения графика с осью имеют вид , поэтому для их нахождения нужно взять , подставить в функцию и найти .

124. Точки пересечения графика с осью имеют вид , поэтому нужно взять , подставить в функцию и найти . Можно найти симметричную точку.

125. П р и м е р. Построить график функции

126. Решение. 1) Найдём вершину параболы, для этого найдём производную и приравняем её к нулю.

127. . Тогда и

128. Подставим это значение в функцию и вычислим .

129. .

130. Следовательно, вершина находится в точке .

131. 2) Найдём точки пересечения параболы с осями координат.

132. С осью тогда .

133. Откуда получаем . Точки

134. С осью : , тогда . Точка и симметричная ей точка .

135. По результатам исследования построим график.

148. УПРАЖНЕНИЯ

150. Построить график функции.

151. 1.

152. 2.

153. 3.

154. 4.

155. 5.

156. 6.

157. 7.

158. 8.

159. 9.

160. 10.

166. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ

167. ФУНКЦИИ НА ОТРЕЗКЕ

168. Выясним, в каких точках отрезка непрерывная функция может принять наибольшее и наименьшее значения.

169. Пусть функция , , непрерывна на отрезке , дифференцируема во всех точках этого отрезка и имеет на нём конечное число критических точек.

170. Очевидно, что если эта функция монотонна на отрезке , то наибольшее и наименьшее значения достигаются на концах этого отрезка (см. рис.12).

171. Если функция не является монотонной, то своё наибольшее значение на отрезке она достигает либо в одной из точек максимума, либо на одном из концов этого отрезка. Точно так же наименьшее значение на отрезке функция достигает либо в одной из точек минимума, либо на одном из концов отрезка (см. рис.13).

181. Рис.12 Рис.13

183. Обобщая наши наблюдения, можем составить правило нахождения наибольшего и наименьшего значений функции на отрезке.

184. Чтобы найти наибольшее и наименьшее значения непрерывной на отрезке функции нужно:

185. 1. Найти критические точки, принадлежащие отрезку и вычислить значения функции в этих точках.

186. 2. Вычислить значения функции на концах отрезка , то есть найти и .

187. 3. Из полученных значений функции выбрать наибольшее и наименьшее.

188. П р и м е р. Найти наибольшее и наименьшее значения функции

189. на отрезке

190. Решение. 1) Найдём критические точки функции:

191. , ,

193. откуда , , .

194. Эти точки принадлежат отрезку . Найдём значения функции в этих точках: ,

195. 2) Вычислим значения функции на концах отрезка:

196. , .

197. 3) Выберем из всех полученных значений функции наибольшее и наименьшее: , =4.

200. УПРАЖНЕНИЯ

201. Найти наибольшее и наименьшее значения следующих функции.

202. 1. на отрезке ;

203. 2. на отрезке ;

204. 3. на отрезке ;

205. 4. на отрезке ;

206. 5. на отрезке ;

207. 6. на отрезке .

208. Задания для самостоятельного решения

209. 7. на отрезке ;

210. 8. на отрезке ;

211. 9. на отрезке ;

212. 10. на отрезке

213. 11. на отрезке ;

214. 12. на отрезке ;

215. 13. на отрезке .

226. Примерный вариант контрольной работы по теме

227. 1. Найдите промежутки монотонности функции

229. 2. Определите момент времени t, в который ускорение прямолинейного движения, совершаемого по закону равно нулю. Какова при этом скорость?

231. 3. В каких точках касательная к кривой параллельна оси абсцисс?

233. 4. Найдите точки экстремума и постройте схематически график функции

234. 10

236. 5. Составьте уравнение касательной к параболе в точке с абсциссой

238. 6. Найдите наибольшее и наименьшее значения функции на отрезке

253. Литература

254. 1. Алимов Ш.А. Алгебра и начала математического анализа 10-11 классы: учебник для общеобразовательных учреждений (базовый уровень) - М.: Просвещение, 2012. - 464 с.

255. 2. Башмаков М.И. Математика: учебник для учреждений нач. и сред.проф. образования. - М.: Издательский центр «Академия», 2010. - 256 с.

256. 3. Валуцэ И.И., Дилигул В.Д. Математика для техникумов на базе средней школы. -М.Наука. Главная редакция физико-математической литературы, 1980. -496 с.

257. 4. Мордкович А.Г. Алгебра и начала анализа 11 кл. в 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) - М.: Мнемозина, 2009 г. - 287 с.

258. 5. Соловейчик И.Л., Лисичкин В.Т.Сборник задач по математике с решениями для техникумов - М.: ООО «Издательский дом «ОНИКС» 21 век» : ООО «Издательство «Мир и Образование».2011. - 462 с.

259. 6. Математика для техникумов. Алгебра и начала анализа: Учебник. Под ред.

260. Г.Н. Яковлева. -3-е изд., перераб. -М.: Наука. Гл. ред. физ.-мат. лит., 1987.-464 с.

27