- Учителю
- Урок по алгебре в 10 классе на тему Тригонометрические функции
Урок по алгебре в 10 классе на тему Тригонометрические функции
Тема. Тригонометрические функции. 10 класс.
Цель. Обобщить и систематизировать знания учащихся .
Развивать умение использовать свойства тригонометрических функций и тригонометрические формулы для решения упражнений, творческую активность, логическое мышление; развивать навыки самостоятельной работы с дополнительной литературой;
Воспитывать самостоятельность мышления, толерантность к размышлениям других учеников. Поставить перед учениками задачи творческого характера для всестороннего изучения данной темы.
Тип урока: урок систематизации и обобщения знаний.
Методы обучения, приемы: работа в группах, словесные, наглядные, практические.
Основные термины и понятия: тригонометрические функции синус, косинус, тангенс, котангенс; свойства функций, тригонометрические формулы
Наглядность: презентация «Тригонометрические функции», таблица, лист самоконтроля
Технические средства обучения: компьютер, проектор
Ход урока:
І. Организационный момент.
ІІ. Объявление темы урока, постановка цели, мотивация учебной деятельности.
Лист самооценки
Тригоно
метрические функции
Тригоно
метрический круг
Тригоно
метрические формулы
Самосто
ятельная работа
Решение
упражн
Допол
нительные баллы
всего
ІІІ. Актуализация опорных знаний.
Раздел 1. Тригонометрические функции.
Блиц-вопросы
1. Синусоида, косинусоид, тангенсоида - названия ...(Графиков)
2. Ось Оу - это ось ... (ординат)
3. Синус, косинус, тангенс, котангенс - это ... функции (тригонометрические)
4. Какая функция называется возрастающей?
(Большему значению аргумента соответствует большее значение функции).
5. Симметрия графика четной функции. (Относительно оси ОУ)
6. Какая функция называется убывающей?
(Большему значению аргумента соответствует меньшее значение функции).
7. Период функции y = sinx? (Т = 2π)
8. Период функции y = tgx? (Т = π)
9. Какая функция называется нечетной? (F (-x) = -f (x))
Вопрос 1.
На каком из рисунков изображен график функции y = sin2x,
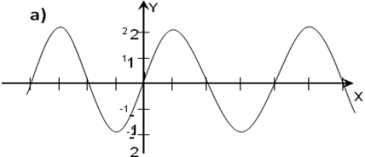
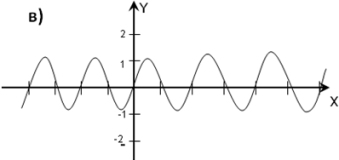
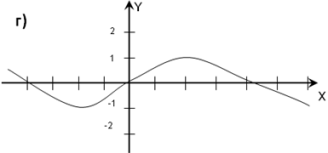
(ответ: В)
Вопрос 2.
Какой из рисунков соответствует графику функции y = cosx + 1?
(ответ: Г)
Вопрос 3. (выберите соответствие между графиком и пословицей)
Любишь с горочки кататься, люби и саночки возить.
Как аукнется, так и откликнется.
Повторение - мать учения.
Раздел 2. Тригонометрический круг.
Решение устных упражнений
1) Найдите и исправте ошибки
А)
y
Б) у В) у
- + + + - +
0
х 0 х 0 х
- + - - - -
у= sinх y=cosх y= tgх
Г) cos (-x)= - cosx; Д) tg (- х) = tg х
2) определите знак tg 170º; cos 200º; ctg 185º; sin 240º.
Раздел 3. Тригонометрические формулы.
Составить формулы. (Работа в парах).
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
Раздел 4. Самостоятельная работа
вариант 1 вариант2
sin2 α +cos2 α =
1+ tg2 α =
sin(-α) =
tg (-α) =
cos (α+β) =
sin (α-β) =
sin 2α =
tg (α+β) =
sin(π- α) =
-
tg α∙ ctg α =
-
1+ ctg2 α=
-
cos (-α) =
-
ctg (-α) =
-
cos (α-β)=
-
sin (α+β)=
-
cos 2α=
-
tg 2α=
-
cos(π- α)=
Раздел 5. Решение упражнений
Упростить выражения:
-cos 400
-cos 400
Упростить выражение:
4sin2
-1
- 1
Вычислить:
1. cos 620cos280 - sin 620 sin 280
2. sin 1120 cos220 - sin 220 cos 1120
3. cos 520cos70 + sin 520 sin 70
4. sin 290 cos160 + sin 160 cos 290
5. 
= tg(400 + 50)
6. 
= tg(550 - 100)
Решение задачи.
Косинус угла при основании равнобедренного треугольника равен 0,8. Найдите синус и косинус угла при вершине этого треугольника.
Решение.
Рассмотрим равнобедренный 
.
По условию cosА = 0,8. Проведем висоту СМ (она также является
биссектрисой и медианой). 
-
прямоуголный.
Пусть А = , С = 
,
+
= 900,
sin
= sin (900 - ) = cos , sin
= 0,8
cos
= 
=
=
0,6
sin 2
= 2 sin cos
= 2·0,8·0,6 = 2·0,48 = 0,96
cos 2
= 1 - 2 sin2
= 1 - 2·(0,8)2 = 1 - 1,28 = - 0,28
Ответ: 0,96; - 0,28.
VІІІ. Подведение итогов
ІХ. Домашнее задание
Подготовиться к контрольной работе.
6