ИСПОЛЬЗОВАНИЕ СВОЙСТВА ОГРАНИЧЕННОСТИ ФУНКЦИЙ ПРИ РЕШЕНИИ УРАВНЕНИЙ

Тема: "ИСПОЛЬЗОВАНИЕ СВОЙСТВА ОГРАНИЧЕННОСТИ ФУНКЦИЙ ПРИ РЕШЕНИИ УРАВНЕНИЙ"

Класс:10

ЦЕЛЬ: познакомить учащихся с нестандартными методами решения уравнений.

ЗАДАЧИ:

1. сформировать умение использовать имеющиеся знания в нестандартных ситуациях;

2. сформировать навыки самостоятельного добывания знаний;

3. сформировать умение анализировать, обобщать;

4. воспитать целеустремленность, взаимоуважение;

5. сформировать навыки коллективного труда.

ХОД УРОКА:

1. Повторение теоретического материала:

• Какая функция называется ограниченной снизу на Х? Приведите примеры.

• Какая функция называется ограниченной сверху на Х?

• Какая функция называется ограниченной на Х?

Найдите множество значений функции. Определите, является ли функция ограниченной?

1. ()

2. ()

3. ()

4. ()

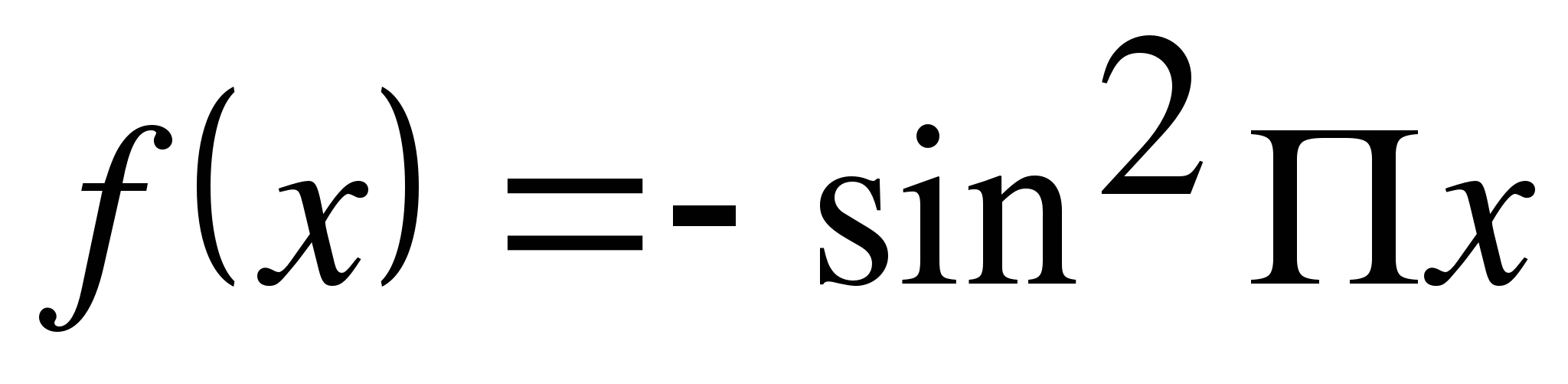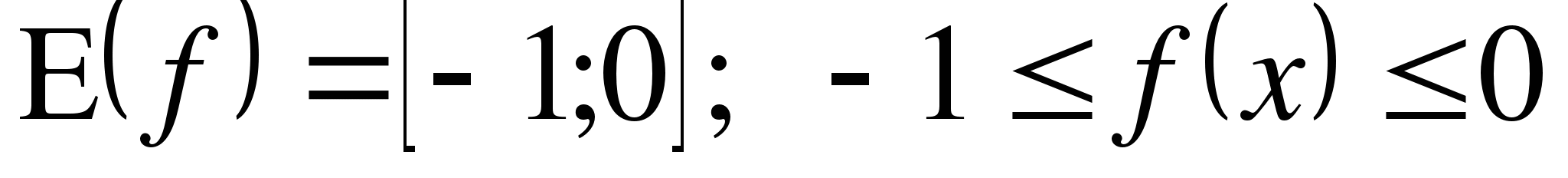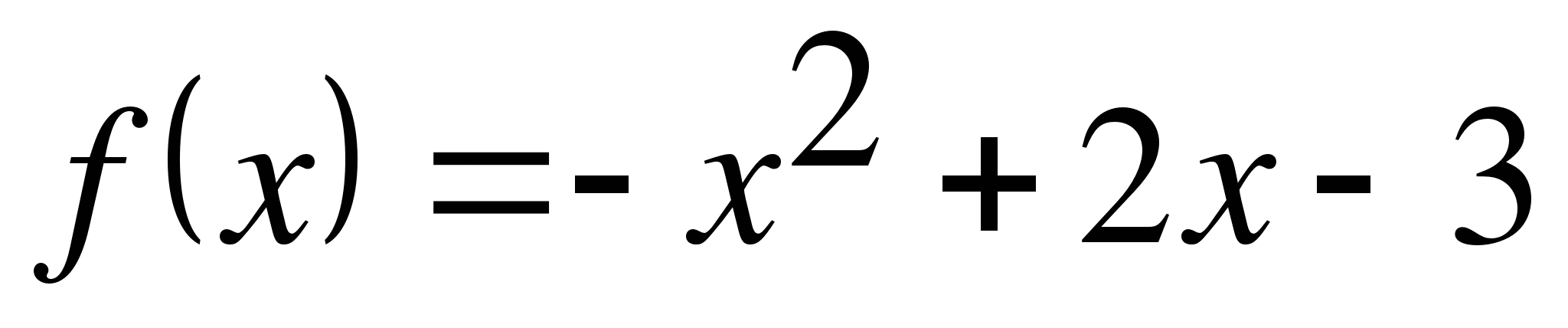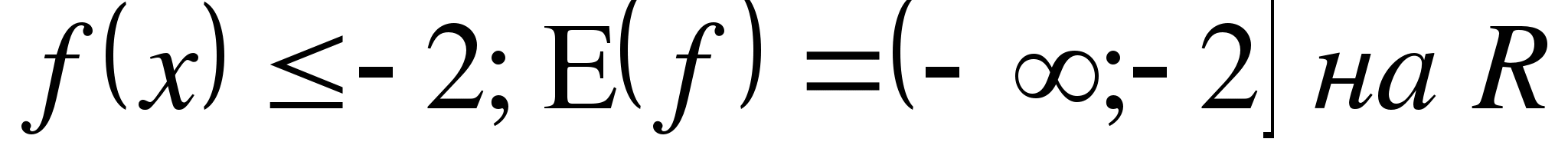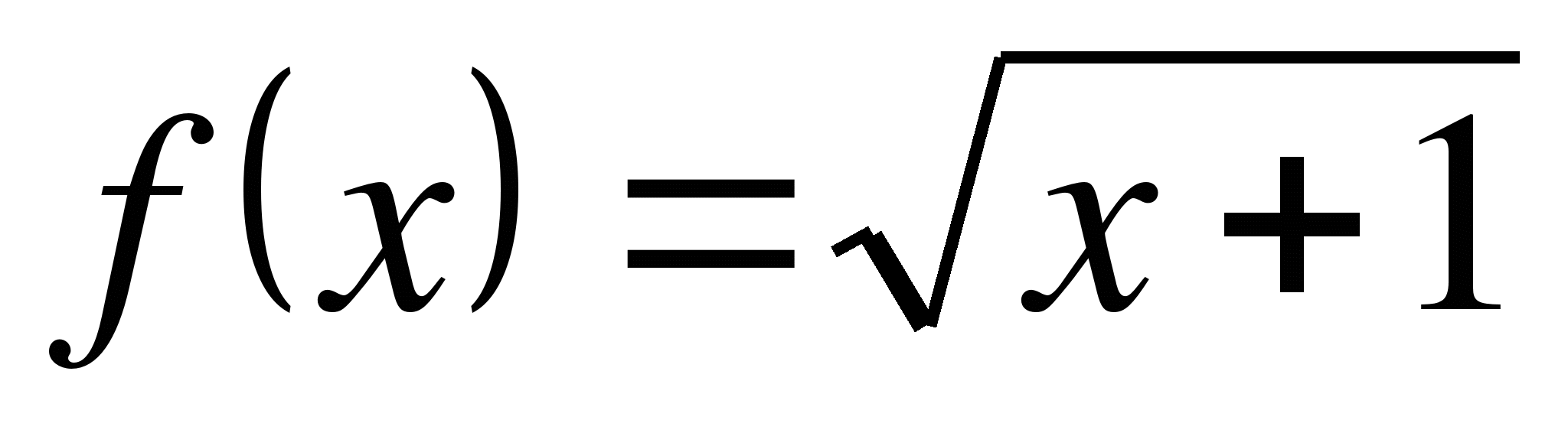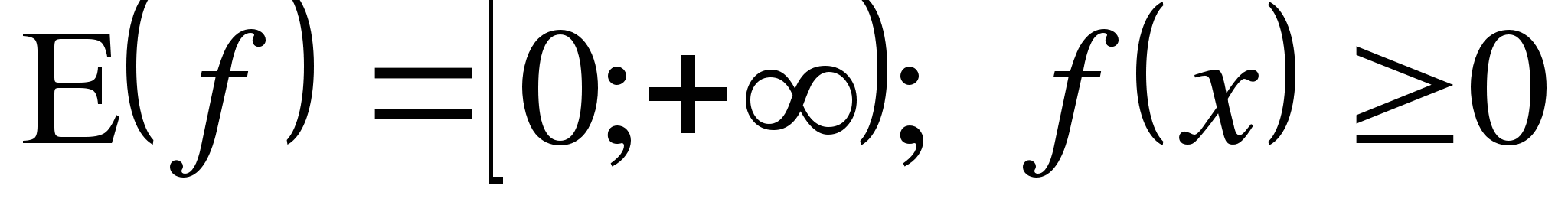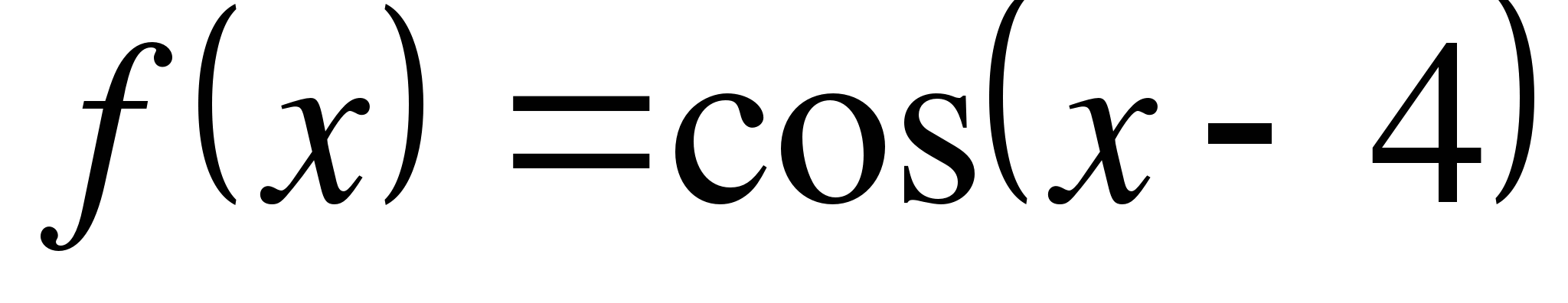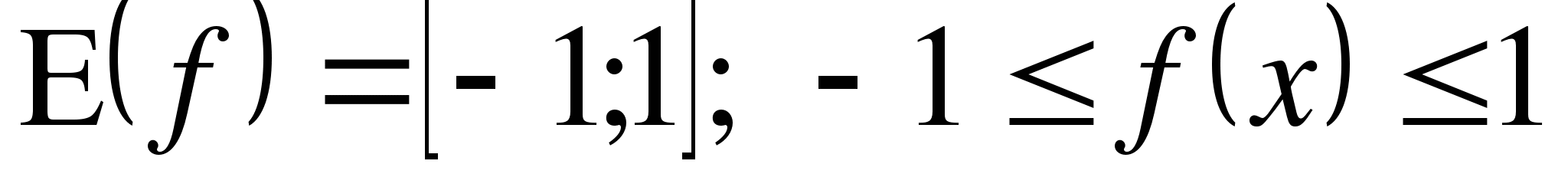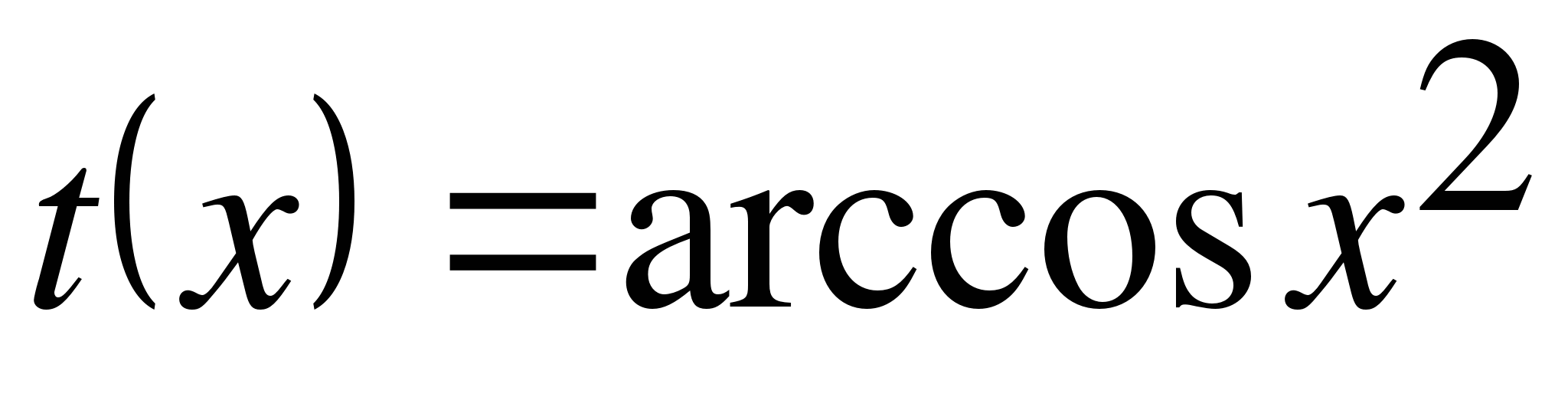5. (t(x) - сложная функция, 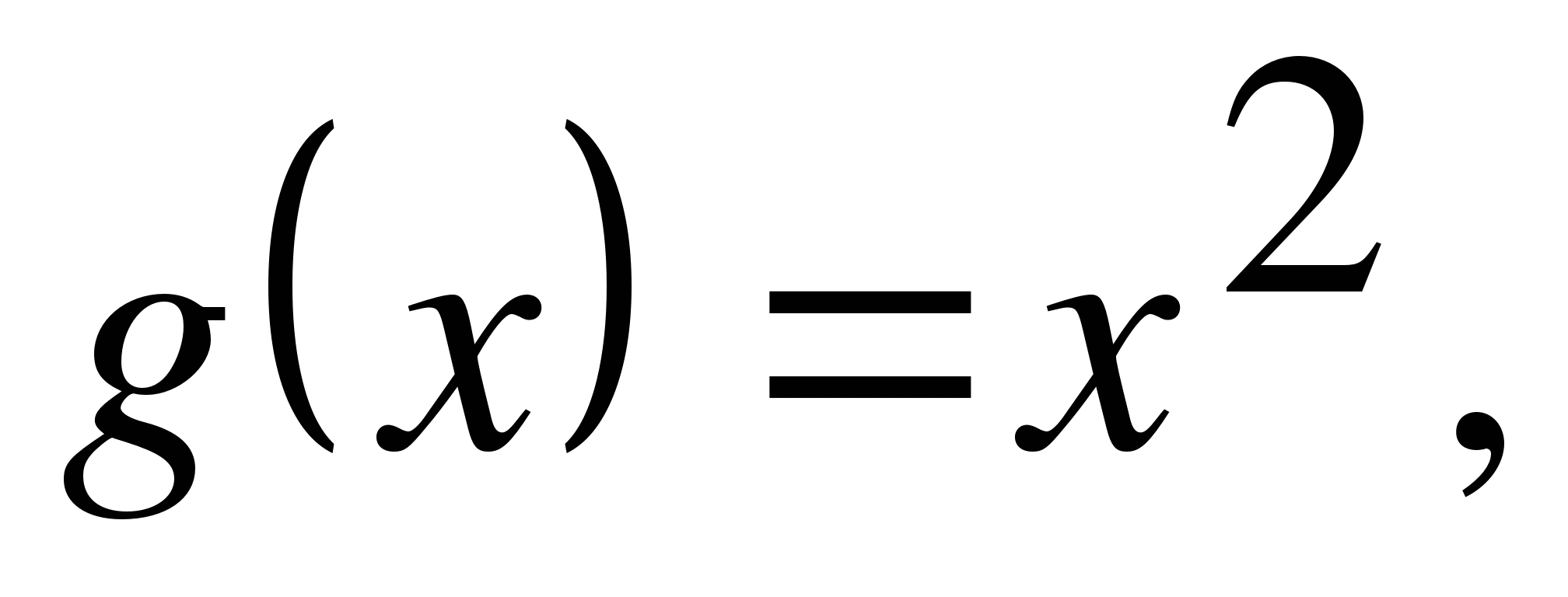t(g) - определена, когда 0≤х²≤1,т.е. на [0;1]; на отрезке [0;1] она убывает, следовательно )

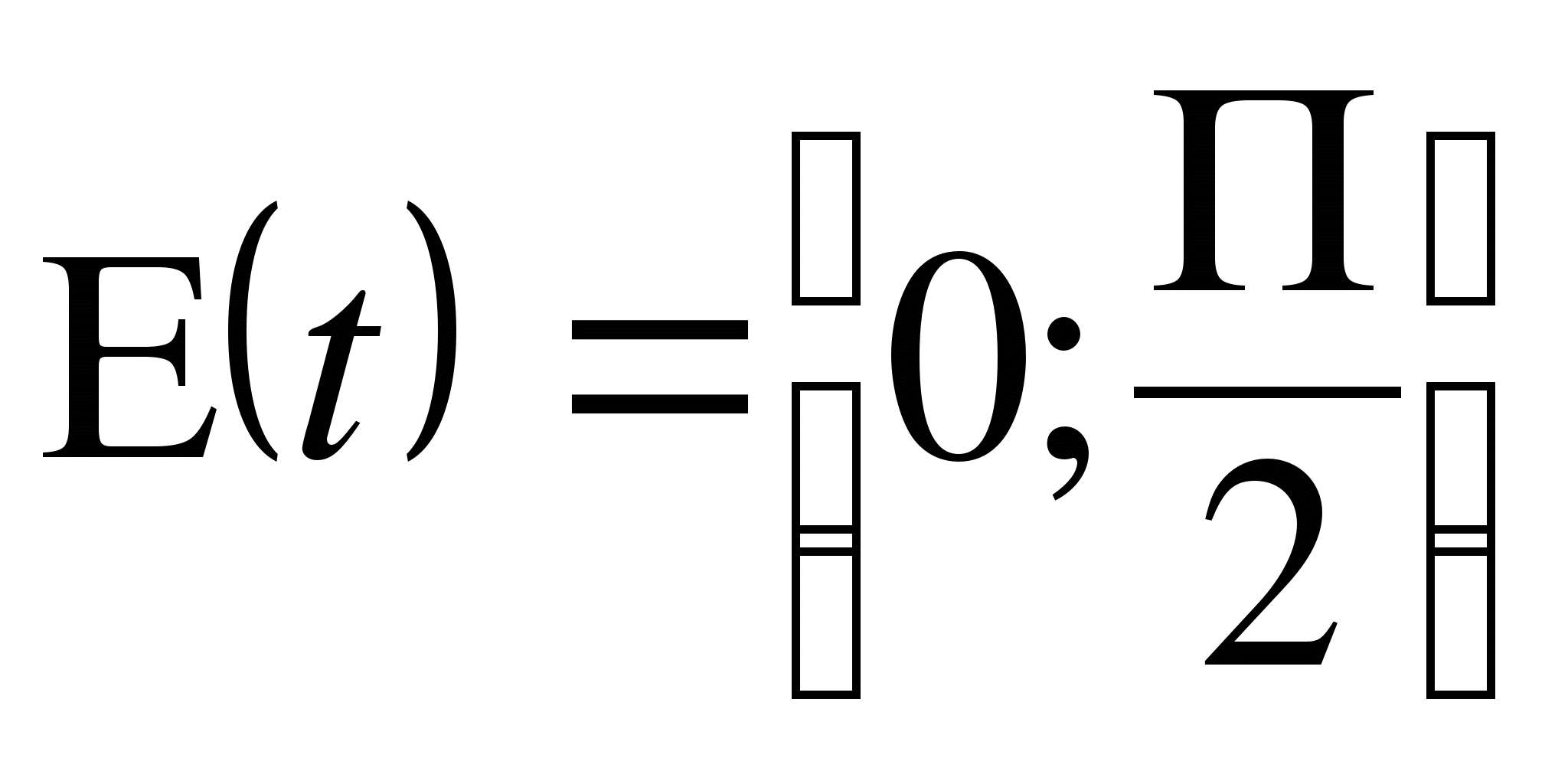2. Изучение новых методов решения уравнений.

На доске записываем уравнение:

Задание: Как, используя свойство ограниченности функций, можно решить уравнение?

Деятельность учащихся и учителя. Учащиеся делятся на группы и приступают к обсуждению методов решения. Когда большинство групп закончили микродискуссию, приступаем к обсуждению метода решения. В процессе обсуждения учащимися составляется план решения:

1. Рассматривают функции f(x) и g(x), стоящие в левой и правой частях уравнения соответственно;

2. Находят область значений каждой функции: 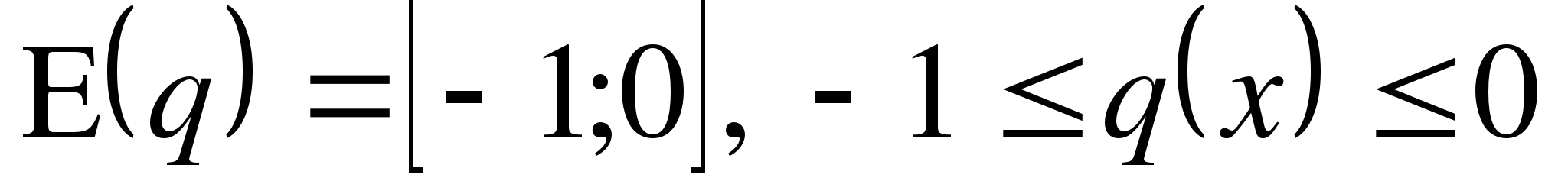, g(x) ≤ 0 , 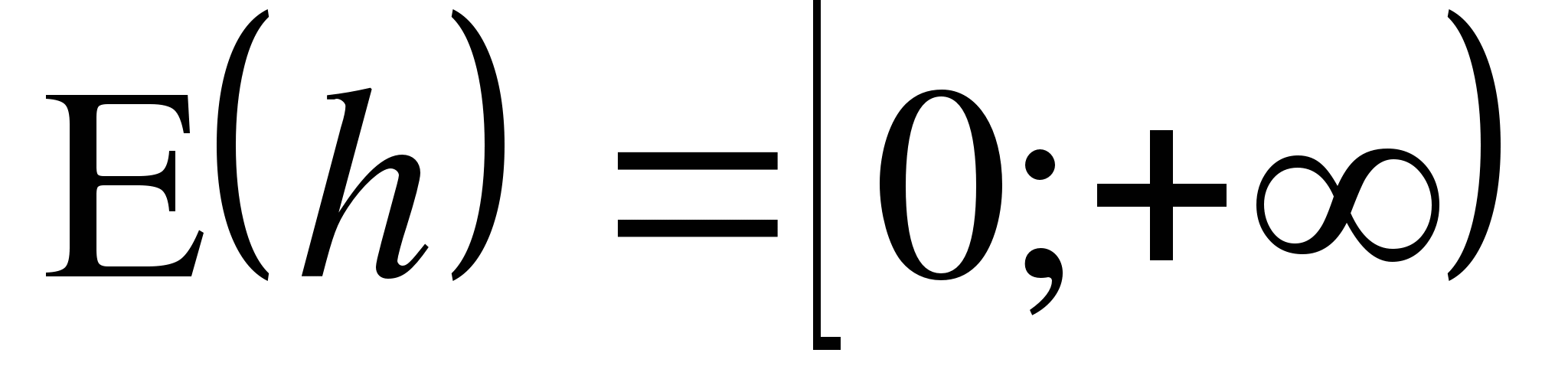, делают выводы об ограниченности функций.

3. Отвечают на вопрос «Когда возможно равенство f(x) = g(x)»

4. Определяют, какое число является корнем уравнения.

Оформление записи:

1) , g(x) ≤ 0

2) , h(x) ≥ 0

3) g(x) = h(x) при g(x) = 0 и h(x) = 0

4) g(-1) = 0, h(-1) = 0, следовательно, х = -1 - корень уравнения.

Ответ: -1.

3. Решение уравнений:

1.

а) ,

б)

в) , следовательно, уравнение не имеет решений.

Ответ: нет решений.

2.

а)

б)

в)

г) ,

, следовательно, х=3 - корень уравнения.

Ответ: х =3.

3. 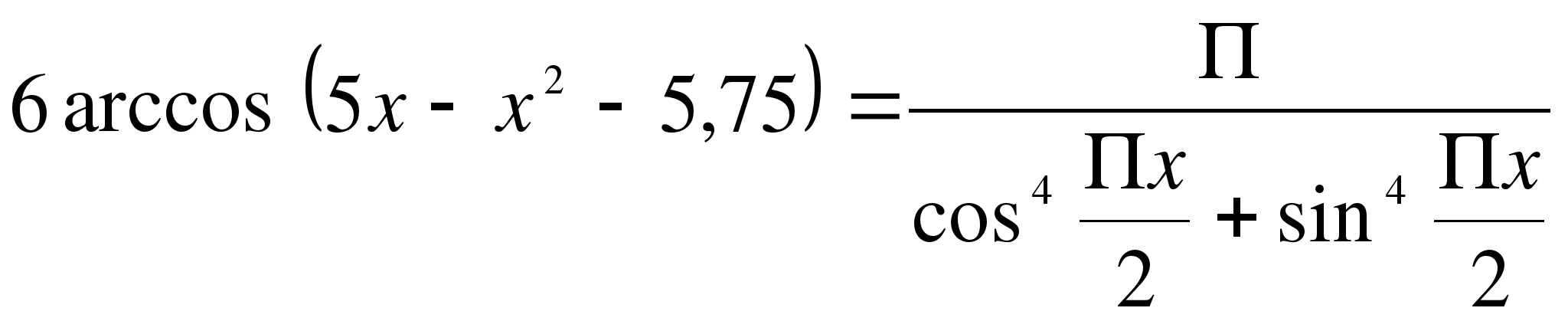(обсуждение по группам)

а)

(ограничение сверху), функция arcos(φ) определена, если -1 ≤ φ(х) ≤ 0,5, тогда ; .

б)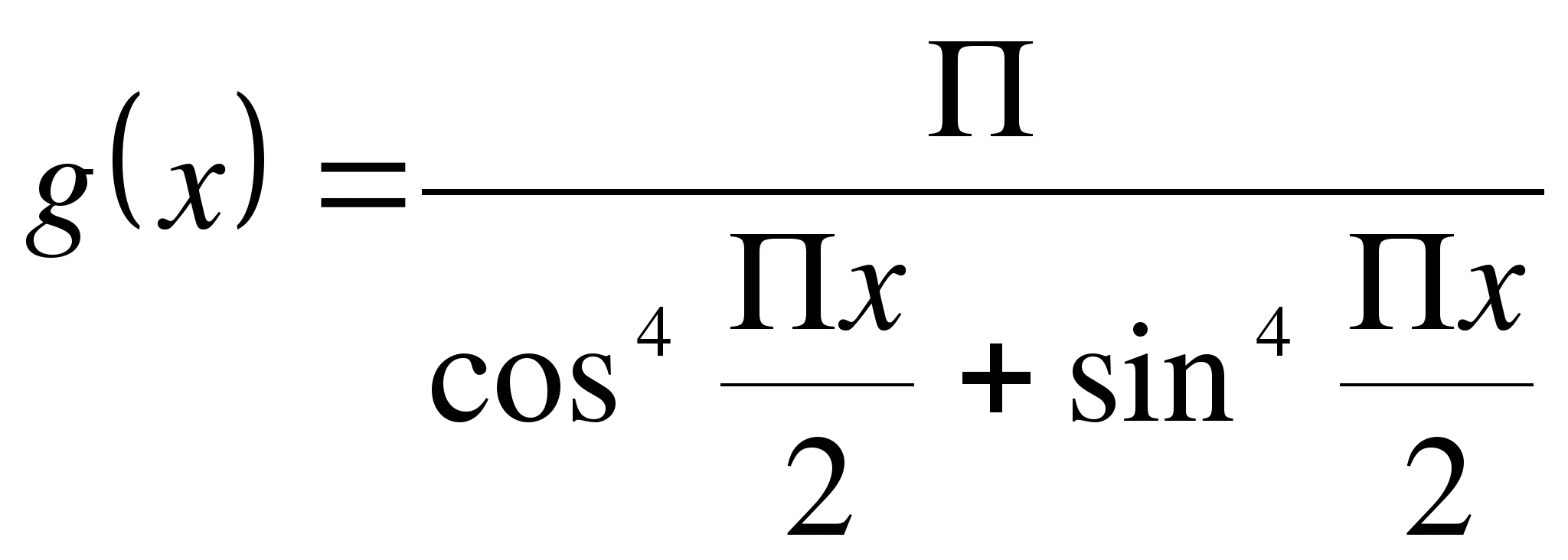

, , ,

,

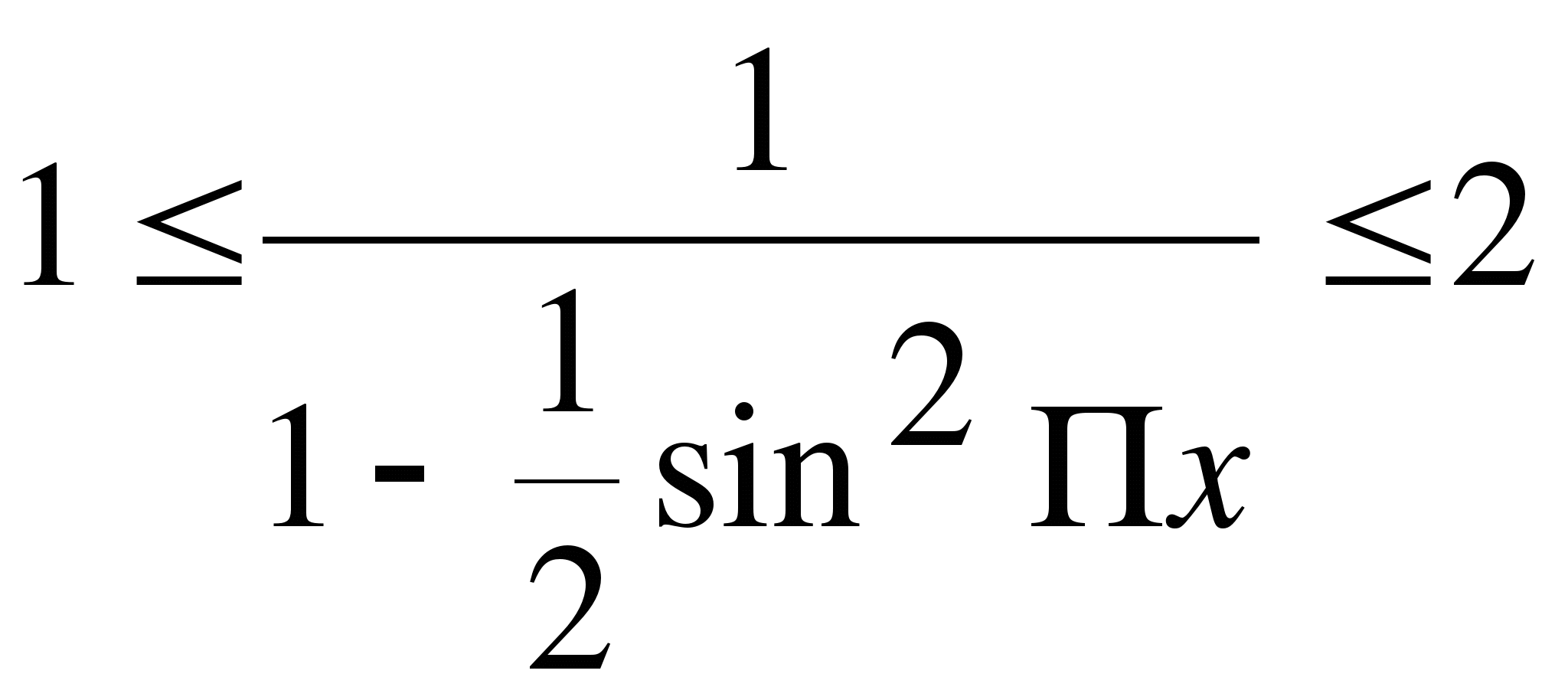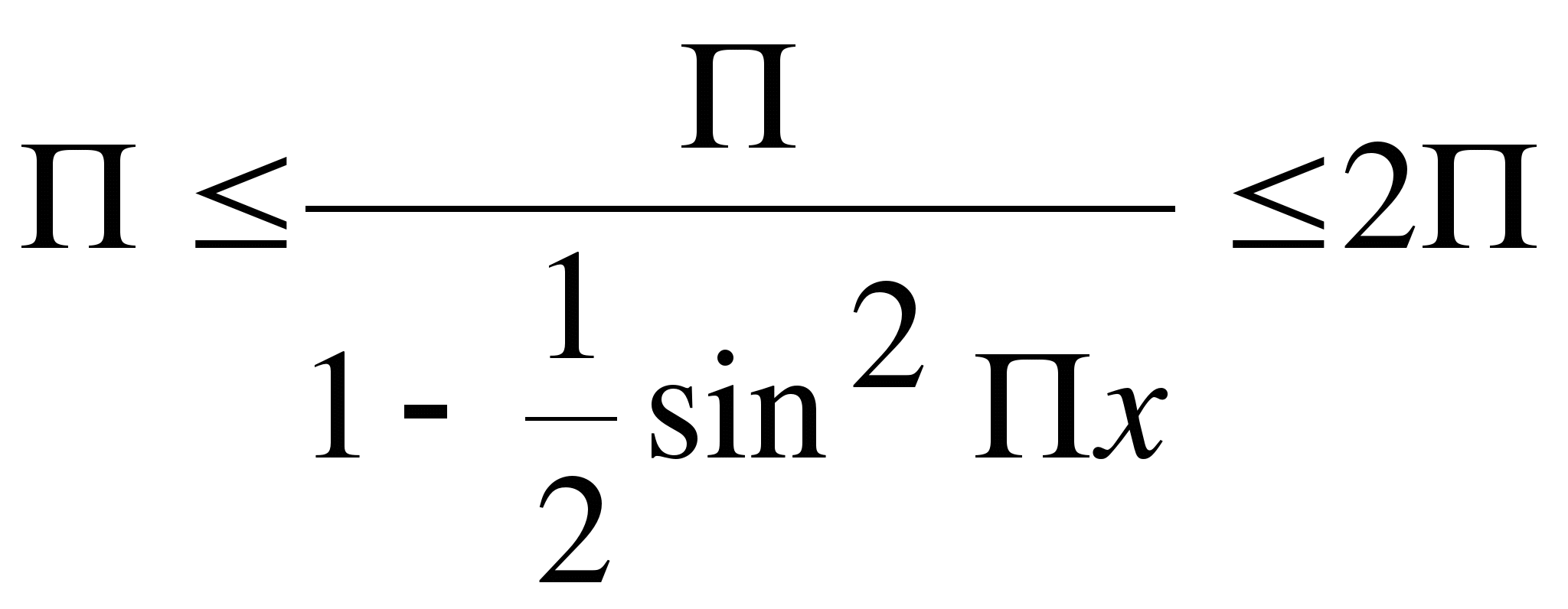
в) , следовательно, f(x) = g(x) возможно при , т.е. f(2,5) = 2Π.

Найдем 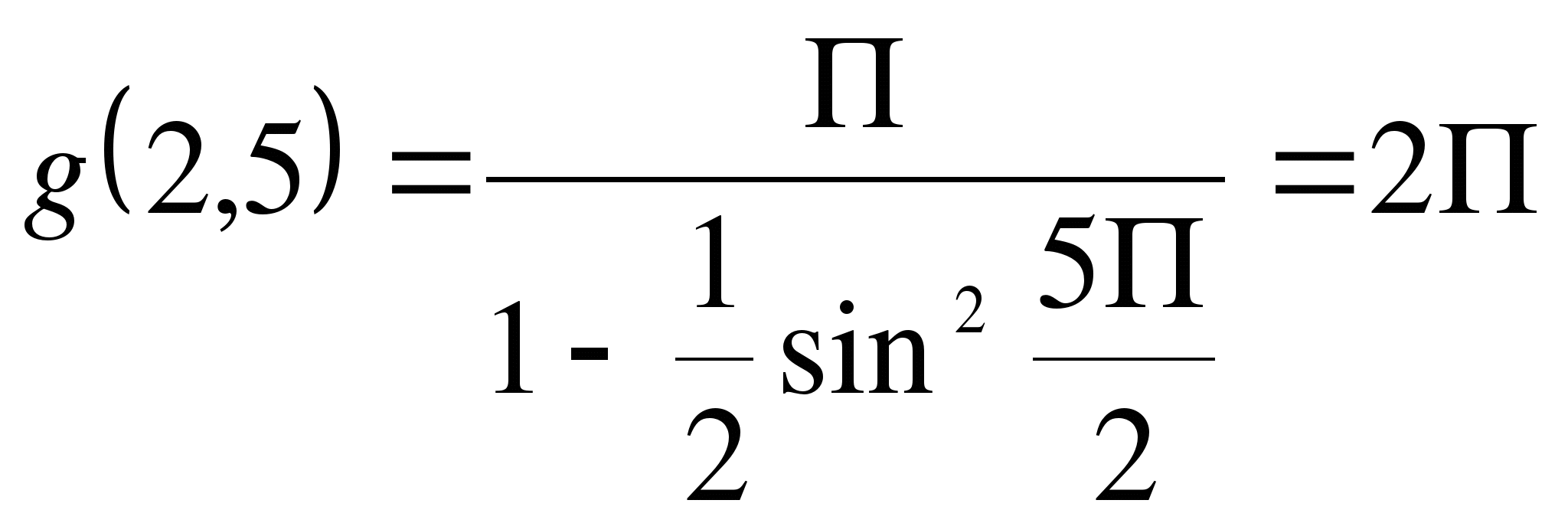→ x=2,5 - корень уравнения.

Ответ: 2,5

4. Подведение итогов урока. Оценка консультантом группы работы каждого члена группы. Оценка работы групп учителем. Рефлексия.