- Учителю
- Конспект урока математики в 5 классе по теме: «Сложение десятичных дробей»
Конспект урока математики в 5 классе по теме: «Сложение десятичных дробей»
Управление образования администрации Топчихинского района Алтайского края
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №2 »
Урок математики
в 5 классе
«Сложение десятичных дробей»
( с использованием компьютерных технологий)
Выполнила: учитель математики
Тимолянова Ольга Викторовна
2014
План-конспект урока
по теме «Сложение десятичных дробей»
-
ФИО учителя:
Тимолянова О.В., учитель математики МБОУ ТСШ №2
Предмет: математика
-
Класс: 5 класс
-
Тема и № урока: «Сложение десятичных дробей», урок № 1.
-
Учебник: Учебник для учащихся 5 класса общеобразовательных учреждений под редакцией коллектива авторов: Н.Я. Виленкин, В.И. Жохов, А.С.Чесноков, С.И. Шварцбурд «Математика 5», издательство «Мнемозина», г.Москва 2010 г;
Цели урока:
Ввести алгоритм сложения десятичных дробей;
формировать у учащихся умение выполнять сложение десятичных дробей;
развивать умение анализировать, сравнивать и обобщать;
развивать устную и письменную речь учащихся;
привить любовь к предмету, желание познать новое.
6. Формы работы учащихся: фронтальная, индивидуальная.
7.Необходимое техническое оборудование: компьютер, мультимедийный проектор
-
Устный счет
-
Вычислите: 28 + 46 35 + 57
33 - 15 78 - 39
-
Прочитайте числа: 0,1; 63,72; 8,08; 0,414; 15,006; 3,7061; 0,31415.
(Уравняйте количество знаков после запятой)
-
Выразите:
а) 7,3 дм (в см);
б) 7,52 м (в см)
в) 6,7 м (в см)
г) 13,5 см (в мм);
е) 356 мм (в см).
-
Сравните числа:
а) 6,727 и 6,7
б) 20,567 и 21,567
в) 0,75 и 0,3456
г) 4,3** и 4,7**
д) **,412 и *,9
ж) *,*** и **,**
-
Объяснение нового материала
Решите задачу:
Токарю нужно выточить деталь, имеющую две части. Длина одной из них 15,7 см, а другой 13, 2 см. Найдите длину заготовки.
(Рисунок на экране)
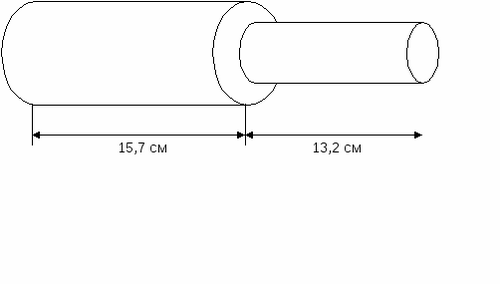

Учитель: Как найти длину заготовки?
Ученик: Чтобы найти длину заготовки надо сложить 15,7 см и 13,2 см.
Учитель: Чтобы решить задачу надо сложить две десятичные дроби. Вы умеете складывать десятичные дроби? (Нет) Что будем делать?
Ученики: Учиться складывать десятичные дроби.
Учитель: Как сформулируем тему урока?
Ученики: «Сложение десятичных дробей»
Учитель: Запишите тему урока «Сложение десятичных дробей». Что хотите вы знать по данной теме? (ответы детей фиксируются на доске)
Учитель: Итак, чтобы решить задачу надо сложить две десятичные дроби. Но вы пока этого делать не умеете. Какие числа вы уже умеете складывать?
Ученики: Натуральные числа, обыкновенные дроби с одинаковыми знаменателями.
Учитель: Как можно решить данную задачу, умея складывать натуральные числа, обыкновенные дроби с одинаковыми знаменателями?
Ученики: 1) Можно выразить 15,7 см и 13,2 см в миллиметры.
2) представить данные десятичные дроби в виде обыкновенных дробей с одинаковыми знаменателями.
Учитель: Рассмотрим два способа решения задачи.
I способ. (1-ый ученик у доски)
15,7 см = 15 см +0,7 см =
= 150 мм + 7 мм = 157 мм;
13,2 см = 13 см + 0,2 см =
= 130 мм + 2 мм = 132 мм
15,7 см + 13,2 см = 157 мм + 132 мм =
= 289 мм = 28,9 см
II способ (2-ой ученик у доски)
15,7 см = ![]() см +
см + ![]() см =
см = ![]() см = 28,9 см
см = 28,9 см
Учитель: Решая задачу мы получили:
15,7 +13,2 = 28,9
Как же выполняется сложение десятичных дробей?
Ученики: Десятые доли складываются с десятыми, единицы с единицами, десятки с десятками.
Учитель: Решите следующие примеры и сделайте вывод
5,17 + 3,12 =
11,124 + 23,2 11
Ученики: Если есть сотые доли, тысячные, то их тоже складывали друг с другом.
Вывод:
Десятичные дроби складываются поразрядно, начиная с младшего разряда. Правило поразрядного сложения позволяет складывать десятичные дроби точно так же, как и натуральные числа «столбиком».
Надо только внимательно писать числа, чтобы одноименные разряды оказались друг под другом.
Н
15,7
13,2
28,9апример:

Введение алгоритма сложения десятичных дробей
(на экране)
Вычислите: 3,7 + 2, 651.
Учитель: Чем данное задание отличается от предыдущих?
Ученики: Разное количество знаков после запятой.
Учитель: Как следует поступать в данном случае?
Ученики: Уравнять количество знаков после запятой.
Учитель: Почему вы так думаете?
Ученик: При сравнении десятичных дробей с разным числом знаков после запятой мы уравнивали количество знаков.
3,700 + 2,651.
Учитель: Записываем дроби друг под другом так, чтобы запятая была под запятой.
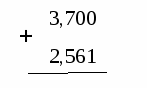
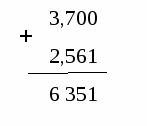
Выполняется сложение, как сложение натуральных чисел,
не обращая внимания на запятую.
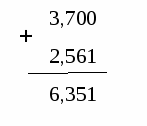
В полученном результате поставить запятую
под запятыми обеих слагаемых.
Записать ответ.
План действий
Решение
-
Уравнять количество знаков после запятой
3,700 + 2,651.
-
Записать дроби друг под другом? Так чтобы запятая оказалась под запятой.
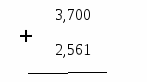
-
Выполнить сложение, как сложение натуральных чисел, не обращая внимания на запятую
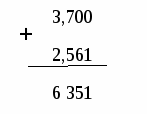
-
Поставить запятую в сумме под запятой в слагаемых
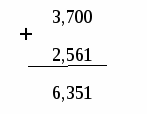
-
Записать ответ
3,700 + 2,651=6,351
3. Усвоение алгоритма
-
Вычислите (устно):
2,3 +4,5 3,17 + 2,13
6,1 + 4,5 0,51 + 12
-
Найдите сумму (у доски 4 человека):
7,21 +3,725 0,46 +48,504 8,003 + 12,7 122,256 + 195
-
Закрепление
№1186 (а,б, в, г)-самостоятельно, затем проверка (решение на экране)
№1184 У доски два человека
Как удобнее решать данную задачу?
После решения задачи обсудить применение сложения десятичных дробей.
№1192 (а,б) один ученик решает у доски, остальные в тетрадях самостоятельно, затем проверяют.
-
Итог урока
-
Творческое задание
Задание (работа в парах):
Придумать друг другу по два примера на сложение десятичных дробей, затем проверить друг друга и поставить оценку.
6. . Постановка домашнего задания.
п. 32
выучить алгоритм сложения десятичных дробей
№1228 (а, б, в)
№1229 (а, б, в)