Урок-зачет на тему Логарифмы (10 класс)

Урок-зачёт.

Тема: «Логарифмы»

Цели:

• Проверить теоретические и практические знания учащихся по изученному материалу;

• Способствовать реализации полученных знаний при выполнении заданий различного уровня сложности;

• Формировать у учащихся чувства взаимоответственности и самоутверждения, самоанализа и самооценки.

Ход урока.

1. Организационный момент.

О каком математическом изобретении великий французский математик и астроном Лаплас сказал, что оно, «сокращая вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов»? (Логарифм).

Я зачитаю слова математика Бриггса, обращённые Джону Неперу: «Милорд, я предпринял это долгое путешествие только для того, чтобы видеть Вашу особу и узнать, с помощью какого инструмента разума и изобретательности вы пришли к мысли об этом превосходном пособии для астрономов, а именно - о логарифмах; но, милорд, после того, как Вы нашли их, я удивляюсь, почему никто не нашёл их раньше, настолько лёгкими они кажутся после того, как о них узнаешь».

Итак, изобретателями логарифмов оказались:

Изобретатели логарифмов

Англ. математик - Джон Непер (1550-1617)

Швец. математик - Иобст Бюрги (1552-1632)

Наш урок - урок-зачёт, посвящён логарифмам.

Мы разбили класс на 4 команды, выбрали знатоков - консультантов команд.

У каждой команды лежит на столе лист учёта знаний. В случае правильного ответа ставим «+». Каждый получит оценку знаний по данной теме.

2. Устный опрос.

Учащиеся должны показать теоретические знания по данной теме.

1. Определение логарифма.

Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести основание а, чтобы получить число b.

2. Записать на доске основное логарифмическое тождество, прокомментировать его.

3. Перечислить основные свойства логарифмов (записать их заранее за доской).

4. При каких условиях выполняются данные свойства?

Если а>0, a≠1, x>0, y>0. P - любое число.

5. Записать на доске формулу перехода от одного основания логарифма к другому основанию.

6. Дать определение логарифмической функции.

7. Перечислить свойства логарифмической функции:

1. D(y) = R+;

2. E(y) = R;

3. y(x) возрастает при a>1;

y(x) убывает при 0<a<1.

8. Определение натурального логарифма.

9. По какой формуле находится производная логарифмической функции.

Теоретически вы подкованы, проверим ваши умения и навыки.

3. Устно.

Ученики должны показать знания свойств логарифмов и умение их использовать при решении.

Тест.

Вычислить:

1. Log₂ 16 - log₈ 64

a) 1 б) 2 в) 3 г) 4;

2. Log_0,5 2 - log₂

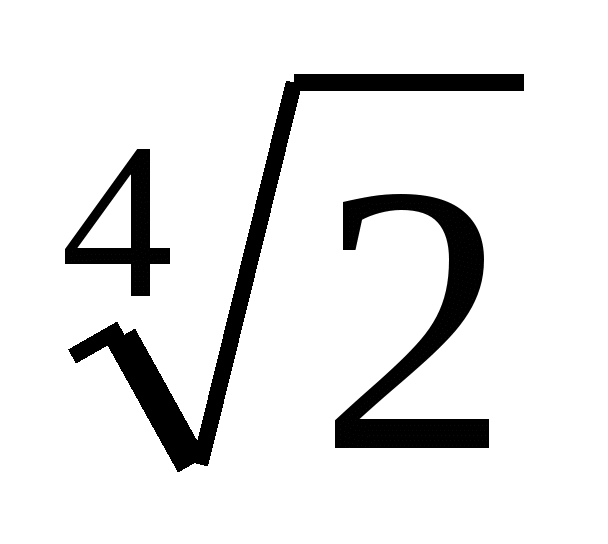
а) 1 б) 0,25 в) -1,25 г) - 0,75;

3. 3^log₃18 - log₂log₃81

а) 2 б) 16 в) 14 г) 3;

4. - log₉ log₂ 8 - 4

а) 3 б) 2 в) -1 г) 1,5;

5. Определить x, если log₃ x = -1

а) 1/3 б) 3 в) 1 г) -1/3 ;

6. Решить уравнения:

Log_2/3 x = -2 ( 9/4)

Log₅ (x+10) = 2 (15)

Log₈ log₃ x = 0 (3)

Log₅ (2x - 1) = log ₅7 (4)

Log₃ x² = log₃ 4 (±2)

7. Решить неравенства:

Log_0.5 x < 0 ;

Log₄ (-x) > 0 .

4. «Торопись, да не ошибись».

Работа в группе. Учащиеся должны показать умение находить область определения функции.

Найти область определения выражения:

(2;∞)

lg(100 - x )

x >0,

x ≠1

x>4

4

x<100

log₇ x

( -10;∞)

Log_0.5 (x - 4)

x >0,

x ≠1

Ключ: a1 - c2 c1 - c4

a2 - е4 c3 - a4

а3 - d1 d2 - b3

b2 - d3 d4 - e3

b4 - b1 e1 - e2

5. «И в шутку и всерьёз».

1. Самая нелюбимая оценка ученика. (2)

2. Проверка учеников на выживание. (ЕГЭ)

6. Самостоятельная работа (тест).

I вариант.

1. Вычислите: log₂ 400 - log₂25

1) 8 2) 2 3) 3 4) 4

2. Упростите выражение: log₂3+log₂ 24-log₂ 9

`1) 18 2) 3 3)4 4)log₂18

3. Указать промежуток, которому принадлежит корень уравнения:

А) log₂(1-x) = 4

1) (62;64) 2) (-81;-79) 3) (79;81) 4) (-17;-10)

b) lg5x=2

1) (3;5) 2) (94;96) 3) (14;16) 4) (19;21)

4.Указать область определения функции:

1) (0;3] 2) (0;1000] 3) (3;1000] 4)[1000; +∞)

II вариант.

1.Вычислите: -4log₁₁11³

1) -64 2) 3^-4 3) -12 4) -1

2.Упростите выражение: log₄36-2log₄ 3

`1) 0 2) 1 3)30 4)27

3.Указать промежуток, которому принадлежит корень уравнения:

А) log₂(x+1) = 4

1) (8;10) 2) (14;16) 3) (6;8) 4) (4;6)

B) lg4x=2

1) (3;5) 2) (24;26) 3) (94;96) 4) (19;21)

4.Указать область определения функции:

1) (0;3] 2) (0;1000] 3) (3;1000] 4)[1000; +∞)

7. Домашнее задание.

8. Итог урока.

4