Тематические материалы для подготовки к уроку математики на тему Место точек на координатной плоскоксти

Изображение на комплексной плоскости множества точек, заданных несложными уравнениями и неравенствами

1. (a) На диаграмме Аргана отметьте точки A и B, соответствующие комплексным числам 1 - 3i и 5 - i соответственно.

(b) (i) Отрезок AB является диаметром окружности C. Найдите радиус и координаты центра окружности.

(ii) Запишите уравнение окружности C в форме |z - z₀| = k.

2. Даны комплексные числа: z₁ = 1 + i и z₂ = iz_1.

(a) (i) Запишите z₂ в форме a + ib.

(ii) Найдите модуль и аргумент z₂.

(b) На диаграмме Аргана отметьте точки, соответствующие комплексным числам z₁ и z₂.

(c) На этой же диаграмме изобразите место точек z, удовлетворяющих уравнениям:

(i) |z - z₁| = |z - z₂|

(ii) arg (z - z₁) = arg z₂

3. Tочка P комплексной плоскости соответствует комплексному числу z = x + i y.

В каждом случае изобразите место точек P, удовлетворяющих уравнениям:

(a) | z - 4 + 3i | = 3

(b) | z - 4 + 3i | = | z - i |

4. Даны комплексные числа: u = 21 + 12i, v = 12 + 0i и w = 0 + 21i, представляющие на комплексной плоскости точки U, V и W соответственно.

Tочка P комплексной плоскости соответствует комплексному числу z = x + i y.

(a) В каждом случае на отдельных диаграммах изобразите место точек P, удовлетворяющих равенствам:

(i) |z - u| = 12

(ii) arg (z - v) =

(iii) |z - v| = |z + w|

(b) При |z - u| = 2|z - v|, место точек P представляет окружность. Найдите радиус окружности и комплексное число, соответствующее ее центру.

5. (a) На диаграмме Аргана изобразите множество точек, удовлетворяющих неравенству: |z - 2i|  1

(b) Найдите наименьшее и наибольше значения аргумента комплексного числа z, удовлетворяющего неравенству |z - 2i|  1. Ответ выразите через .

Ответы

1. (a)

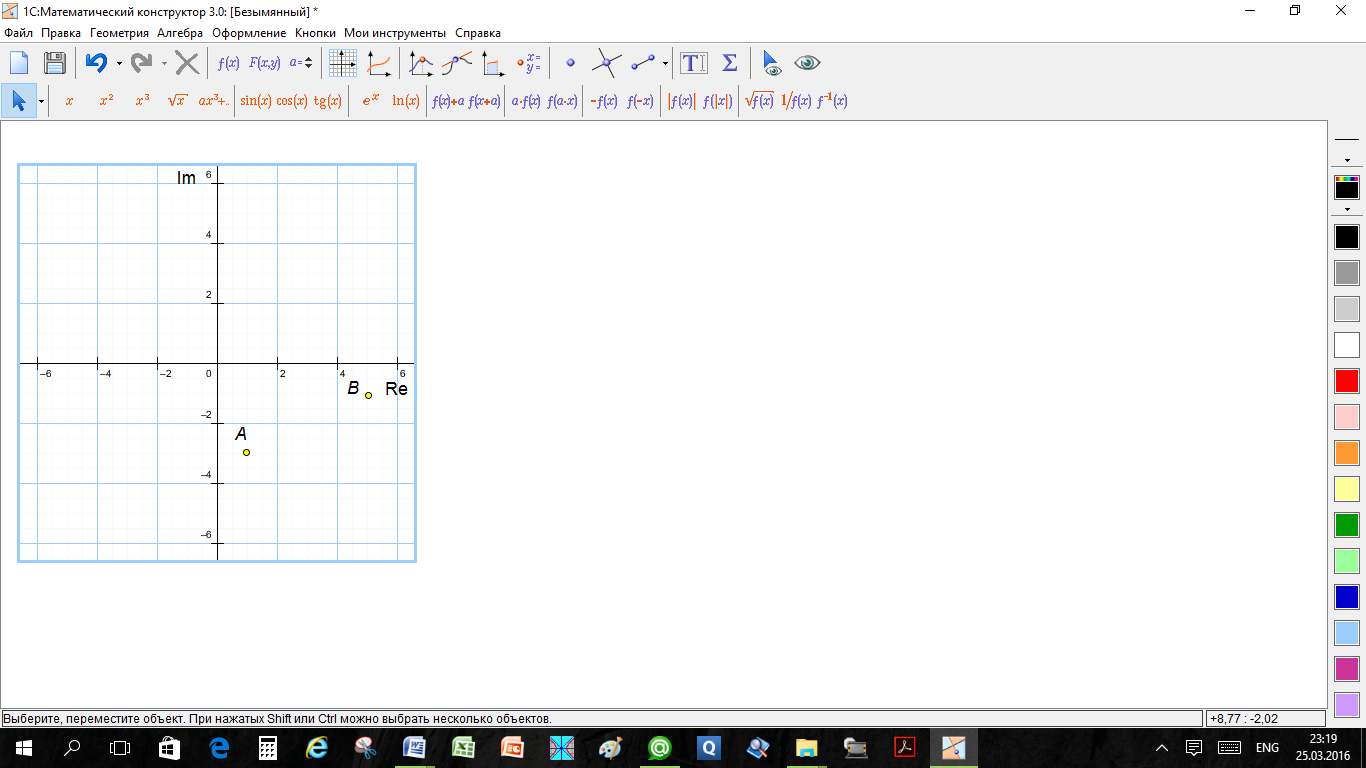
(b) (i) центр - (3 - 2i) , радиус -

(ii)

2. (a) (i) + i

(ii) |z₂| = 2, arg z₂ =

(b)

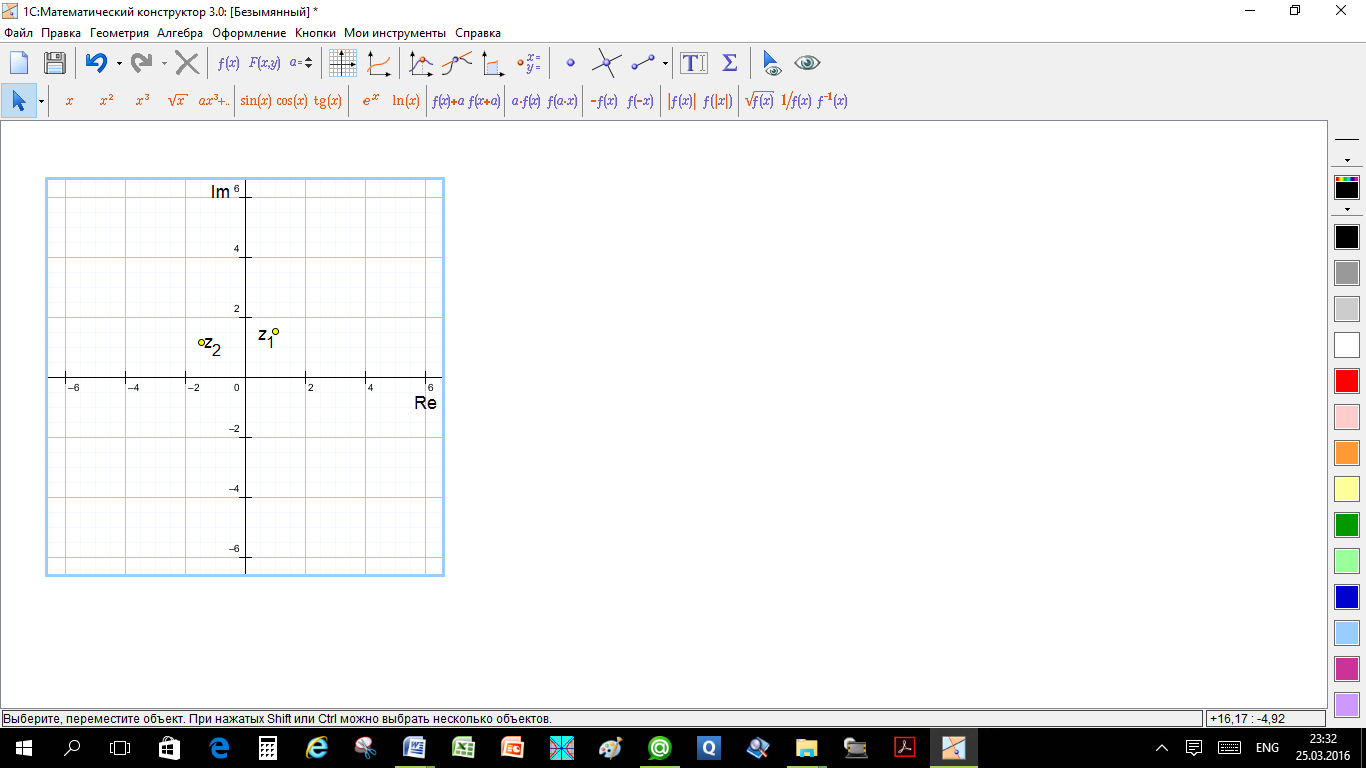
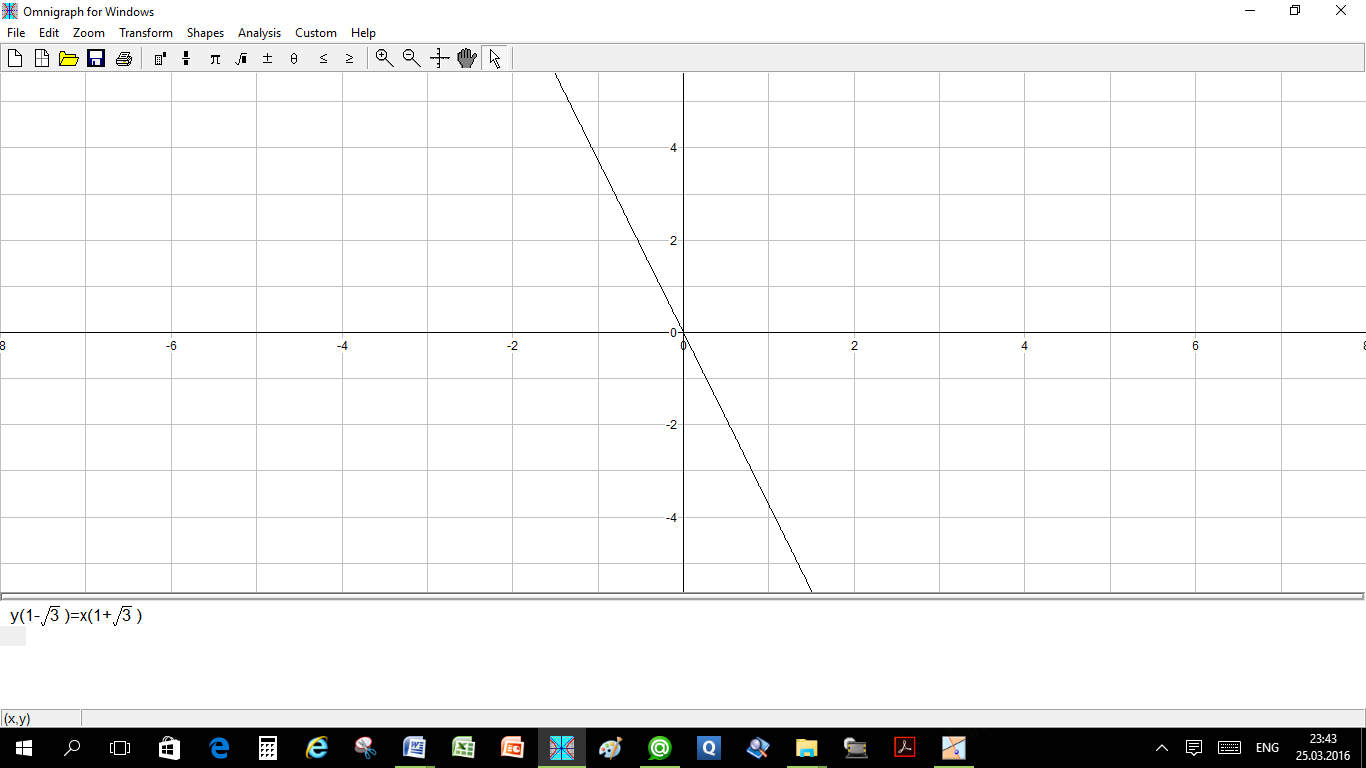
(c) (i) серединный перпендикуляр, проходящий через точку (0, 0)

Или прямая

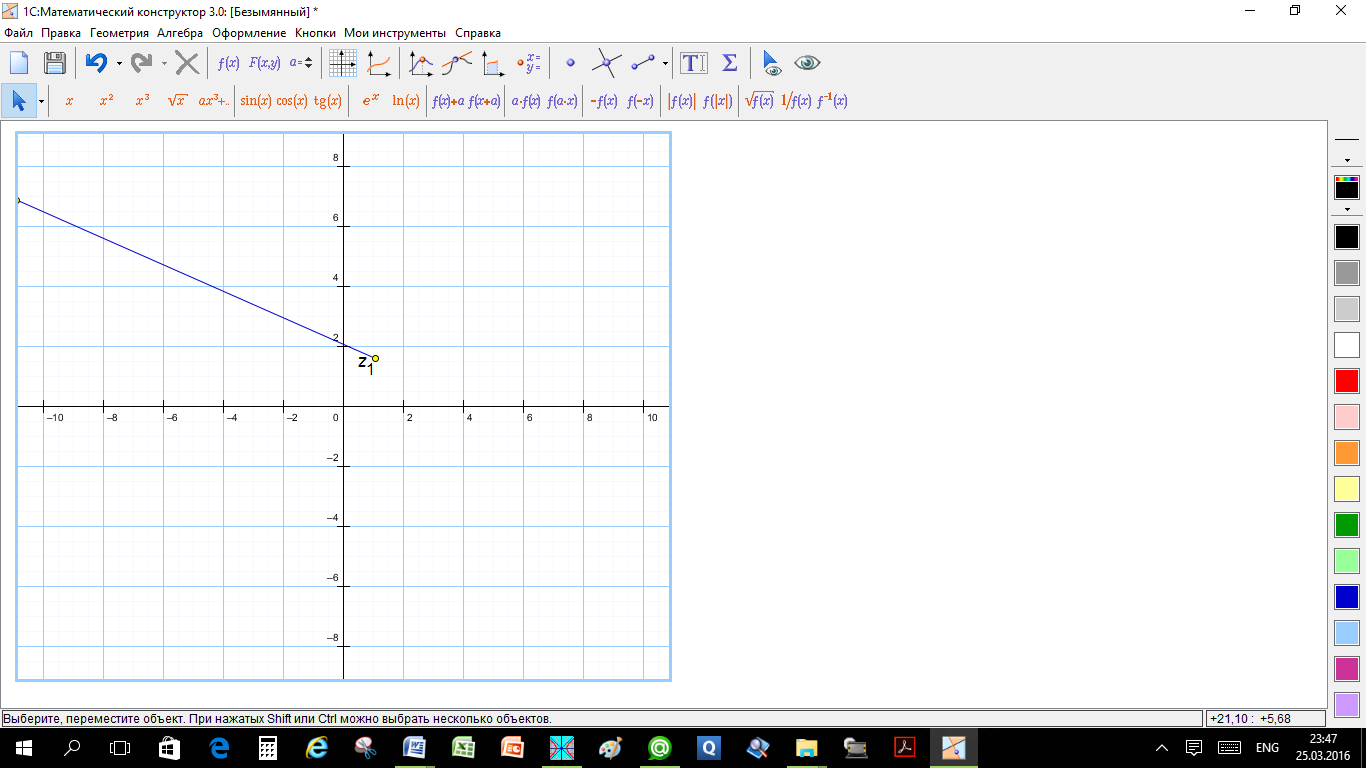
(ii) полупрямая, проходящая через z_{1 параллельно} Oz₂

Или полупрямая, исходящая из точки (1, ) и образующая угол 5/6 с положительным направлением действительной оси

3. (a) Окружность с центром в точке 4 - 3i радиуса 3

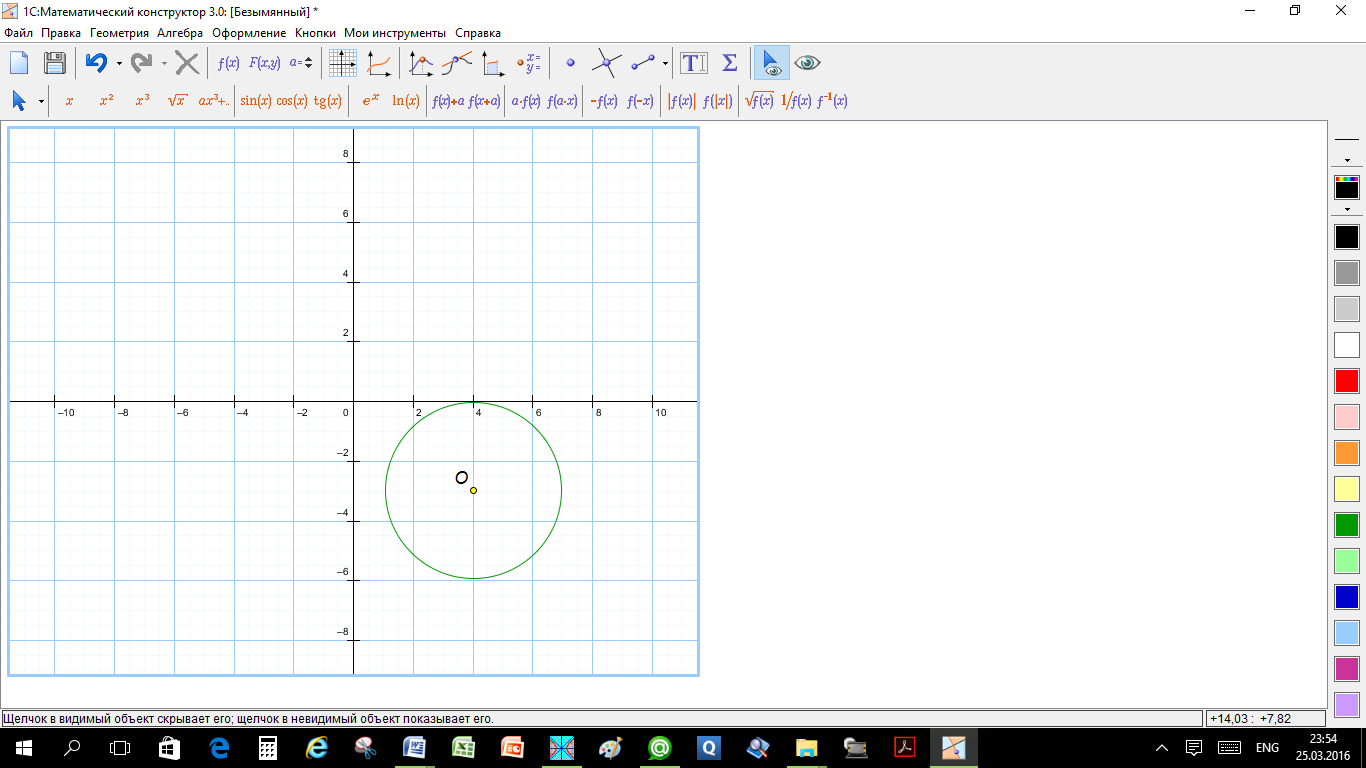
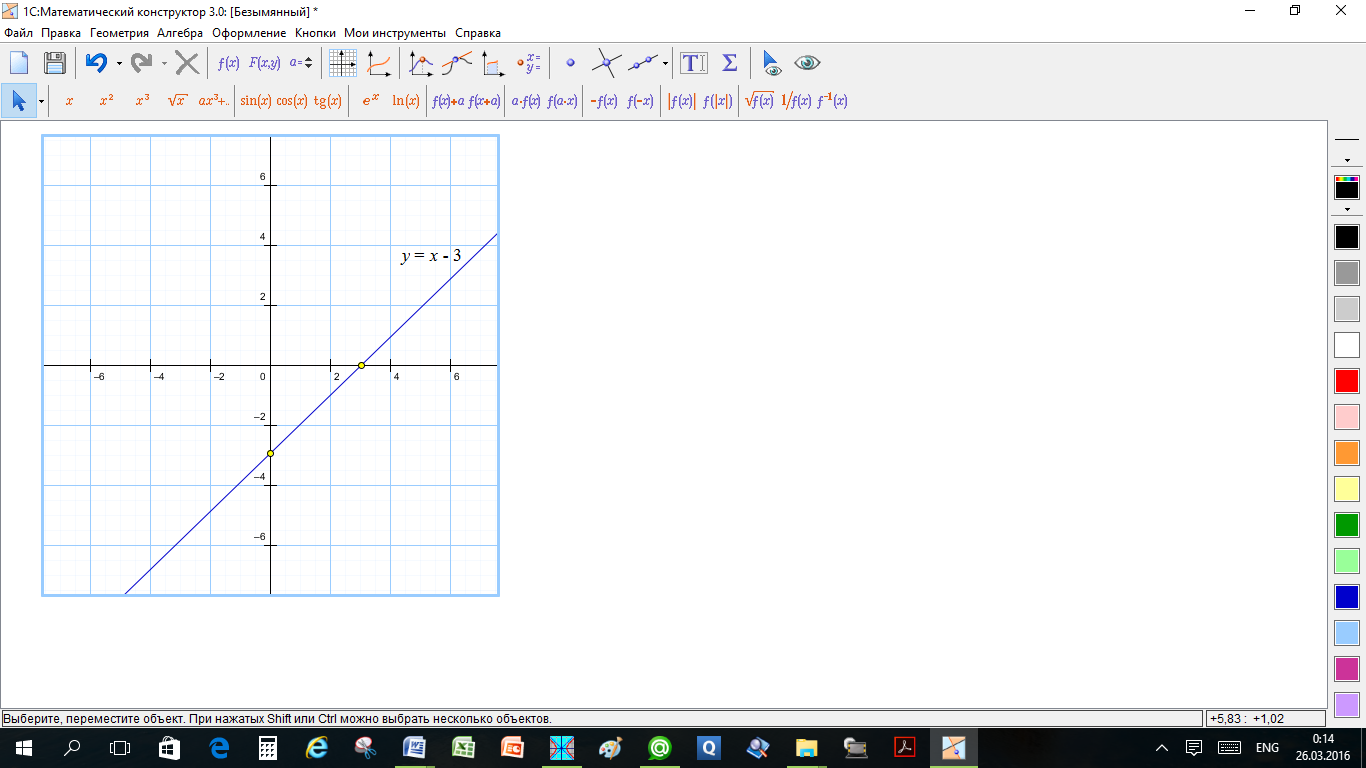
(b) серединный перпендикуляр к отрезку, соединяющему точки 4 - 3i и i

Или прямая y = x - 3

4. (a)(i) окружность с центром в точке (21,12) радиуса 12

(ii) полупрямая, исходящая из точки (12, 0) и образующая угол /4 с положительным направлением действительной оси

(iii) серединный перпендикуляр к отрезку, соединяющему точки V и W

(b) окружность с центром в точке 9 - 4 i радиуса 10

5. (а) круг с центром в точке 2і радиуса 1

(b) наименьший аргумент наибольший аргумент