Урок-марафон Площади фигур. Решение задач

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА ИРКУТСКА ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА - ИНТЕРНАТ № 13

ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ

Учитель математики Афонина Елена Николаевна

Открытый урок

по геометрии

в 8 классе

Тема урока: Площади фигур.

Решение задач.

Класс: 8А

Тема урока: Площади фигур. Решение задач.

Задачи урока: Систематизировать, обобщить знания по применению формул площадей

квадрата, прямоугольника, параллелограмма, трапеции, ромба и треугольника

в ходе решения задач.

Вести работу по развитию устойчивой памяти, внимания; укреплению волевых

качеств, логического мышления.

В ходе проведения самостоятельной работы обучающего характера выявить

пробелы знаний по теме «Площадь».

Способствовать формированию познавательных интересов, воспитывать у детей

осознанное отношение к учёбе.

Оснащение: Опорные таблицы (изображение фигур и формулы площадей), таблички для

решения задач, ТСО (кодоскоп) при решении устных задач.

Структура урока:

Ι.Организационный момент.

(настрой на работу). Сообщаются тема и цели урока. Дается домашнее задание:

п.51 - 53(формулы), № 476(а), № 489(а); дополнительно (индивидуально): по учебнику Погорелова- № 11, с.227; продолжаем подготовку к практической работе: готовим фигуры для нахождения их площадей. (Учителем даются комментарии к выполнению домашнего задания).

ΙΙ.Актуализация знаний.

- На предыдущих уроках мы вывели некоторые формулы для вычисления площадей квадрата, прямоугольника, параллелограмма, ромба, треугольника и трапеции.

1) - Повторим все эти формулы, и их мы будем использовать при решении задач.

(На доске прикреплены фигуры, а таблички с формулами площадей находятся на столе).

- Необходимо к каждой фигуре подставить нужную формулу и прокомментировать.

1. 2. 3.

b

4. 5. 6.

S= (a + b)/2 hS = √p(p - a)(p - b)(p - c),

где p = (a + b + c)/2

S = a²√3 / 4

2) - Итак, сегодня применяя формулы площадей фигур, мы сначала вместе, а в конце урока и самостоятельно займемся решением задач.

- Начнем с решения простейших задач.

(Устно решаются задачи по рисункам, используется интерактивная доска или кодоскоп).

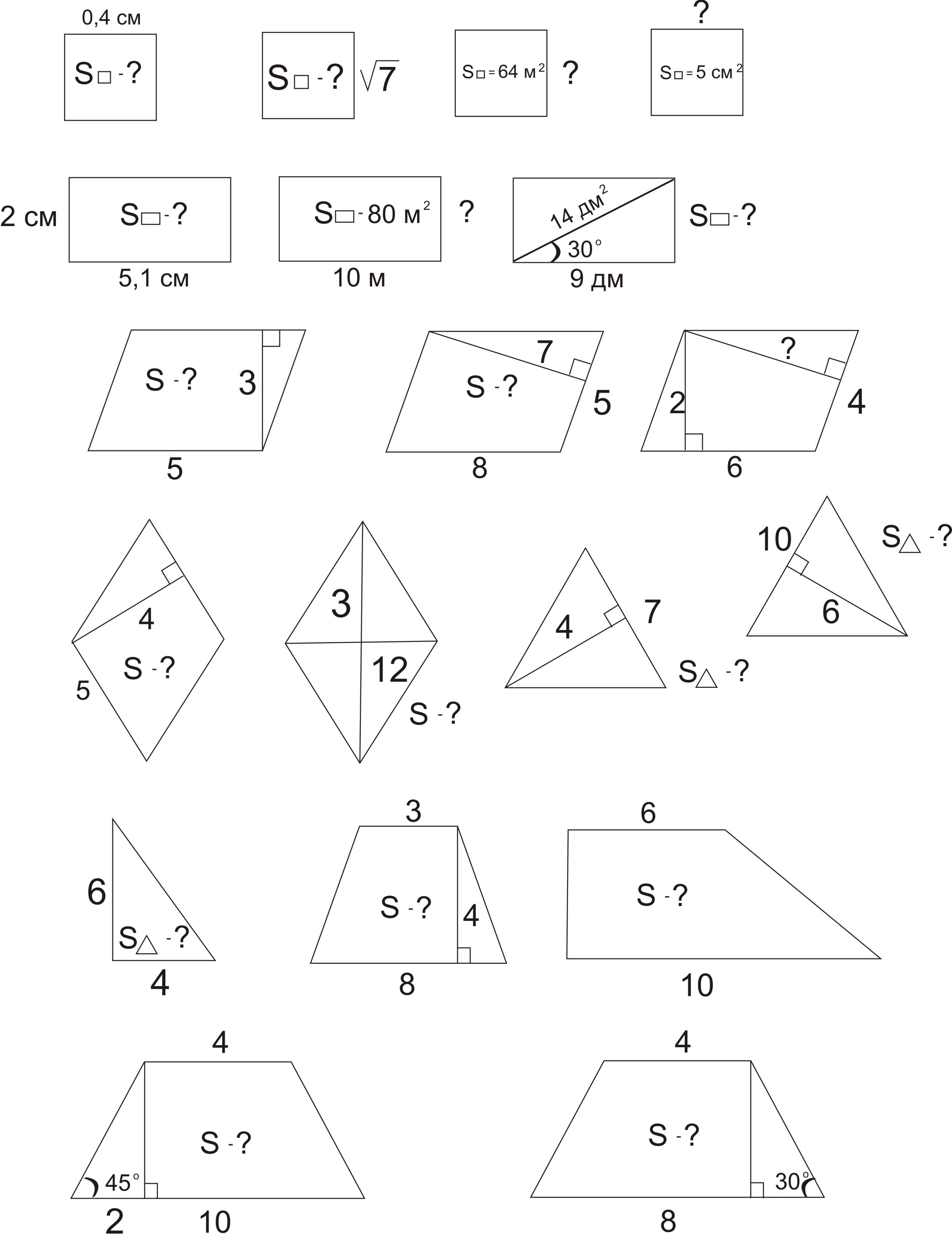
ΙΙΙ.Формирование умений, навыков.

Решение задач (в тетрадях).

1. По рисунку составить условие задачи и выполнить решение. (Разбор задачи у доски

с комментированием).

Дано:

АВСД - параллелограмм

В = 150˚,

АВ = 10 см, АД = 12 см.

Найти:

S пар.

Решение: 1. S пар. = а h

2. ВН - высота.

3. Рассмотрим ∆ АНВ - прямоугольный, А = 180˚ - 150˚ = 30˚,

=> ВН = ½ ×10 = 5 см.

4. S пар. = 5×12 = 60 см².

Ответ: S пар. = 60 см².

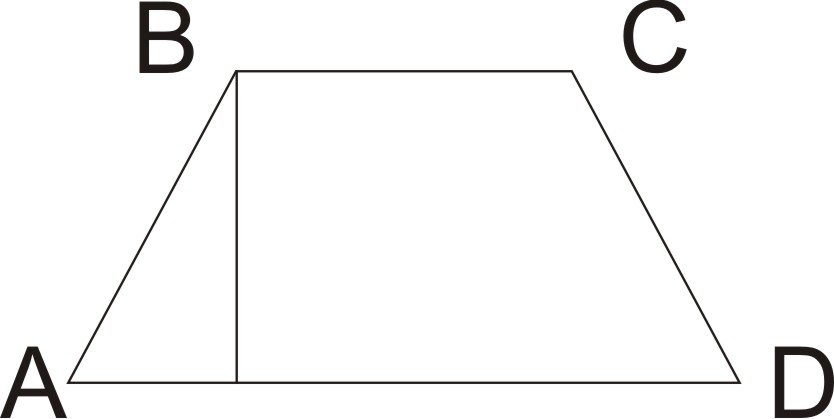2. №482 (по учебнику Атанасяна)

Дано:

АВСД - равноб. трапеция

В = 135˚, ВН - высота,

АН = 1,4 см; НД = 3,4 см.

Найти:

S тр. Н

а + в

Решение: 1.S тр. = --- ×h

2

2. АД = 1,4 + 3,4 = 4,8 (см)

3. СF - высота, СF =1,4 см =>НВСF - прямоугольник,

тогда ВС = 3,4 - 1,4 = 2 (см); т.к. FД = АН = 1,4 см.

4. А = 180˚ - 135˚ = 45˚.

5. Рассмотрим ∆ АНВ - прямоугольный, если А = 45˚, то В = 45˚,

=>∆ АНВ - равнобедренный и ВН = 1,4 (см).

4,8 + 2

6. S тр. = ---- × 1,4 = 3,4 ×1,4 = 4,76 (см²).

2

Ответ: S трапеции = 4,76 см².

3) Индивидуальная работа. (Выполняется учениками, справившимися с решениями предыдущих задач, после проверки учителем).

Дополнительно: № 1. Вычислить площадь равностороннего треугольника со стороной 2√5 см.

№ 2. Найти площадь треугольника со сторонами 5см, 5см, 6см.

( Данные задач записаны на табличках, они расположены на магнитной доске).

(Для решения задачи №1 и №2, при применении формулы нахождения площади равностороннего треугольника вспомните свойства арифметического квадратного корня).

№1 № 2

а = 5 см

в = 5 см

с = 6 см

а = 2√5 см

Решение задачи №1: а²√3 (2√5)²√3 4×5√3

S∆ = --- ; S∆ = ---- = ---- = 5√3 (см²).

4 4 4

Решение задачи №2: (применяя формулу Герона).

5 + 5 + 6

р = ¯¯¯¯¯2¯¯¯¯¯ = 8;

Ѕ∆ = √8 (8 - 5) (8 - 5) (8 - 6) =√8 3 3 2 =3√16 =3 4 = 12 (см²)

4) Самостоятельная работа обучающего характера.

Ι вариант: № 471(а) (прямоугольный ∆: Ѕ∆ = ½ 4 11 = 22 (см²) ).

ΙΙ вариант: № 476(б) (ромб: Ѕромба = ½ 4,6 2 = 4,6 (дм²)).

Дополнительно: № 465 (Ѕпар. = 12 см²).

ІV Итог урока. (Подводится итог урока, выставляются и комментируются оценки за работу на уроке, собираются тетради с самостоятельной работой).