Конспект урока + презентация + раздаточный материал к уроку геометрии для 8 класса «Многоугольники»

Муниципальное автономное общеобразовательное учреждение

«Средняя общеобразовательная школа №5»

Урок геометрии в 8 классе

по теме: МНОГОУГОЛЬНИКИ

Учитель математики:

Палехова Екатерина Викторовна

МАОУ СОШ №5

г. Березники - 2013

Конспект урока

Дата: 2.04.2013 г.

Класс: 8А.

Тема: Многоугольники.

УМК: Л.С. Атанасян, Геометрия 7-9.

Цель:

• образовательная: 1) усвоение знаний в системе; 2) формирование умений и навыков находить площадь, применять теорему Пифагора, теорему о катете, лежащем против угла 30°, соотношения между сторонами и углами прямоугольного треугольника; 2) формирование умений работать с задачей.

• развивающая: развитие памяти, мышления, наблюдательности, внимания; развитие познавательного интереса, развитие умения работать в группе;

• воспитательная: воспитание самостоятельности, аккуратности, умения отстаивать свою точку зрения, умения выслушать других.

Тип урока: Урок обобщения и систематизации знаний.

Форма урока: групповая работа по 5-6 человек.

Оборудование: проектор, раздаточный материал.

План урока

1. Организационный момент (2 мин)

2. Актуализация опорных знаний и умений (10 мин)

3. Физкультминутка (5 мин)

4. Формирование умений и навыков работы с задачей (20 мин)

5. Подведение итогов работы на уроке (2 мин)

6. Задание на дом (1 мин)

Ход урока

Деятельность педагога

Деятельность учащихся

Примечание

Организационный момент

• Приветствие.

• Сообщение темы урока (Многоугольники).

• Спросить цель урока у учащихся, чего они ждут от урока, где можно применить знания по данной теме.

Цель: привести знания в систему, обобщить изученный материал, узнать что-то новое для себя.

Применить полученные знания можно на уроках математики, физики, информатики; в таких профессиях как инженер, строитель, дизайнер, а также в быту (ремонт).

Слайд 1

Актуализация опорных знаний и умений

Ребята, ответьте, пожалуйста, на следующие вопросы:

1. Что изображено на картинке?

2. Какая фигура лишняя?

3. Что объединяет все фигуры?

4. Какие виды многоугольников изображены?

5. Назовите каждую фигуру.

6. Опишите свойства каждой фигуры.

Ответы:

1. Фигуры.

2. Круг.

3. Все фигуры являются многоугольниками.

4. Треугольники и четырехугольники.

5. Прямоугольник, ромб, параллелограмм, квадрат, прямоугольный треугольник, равнобедренный треугольник, треугольник, равнобедренная трапеция.

6. Прямоугольник: противоположные стороны равны, углы по 90°, диагонали точкой пересечения делятся пополам.

Ромб: стороны равны, диагонали взаимно перпендикулярны и точкой пересечения делятся пополам, противоположные углы равны, диагонали делят углы пополам.

Параллелограмм: противоположные углы и стороны равны, стороны попарно параллельны, диагонали точкой пересечения делятся пополам.

Квадрат: стороны равны, углы по 90°, диагонали взаимно перпендикулярны и точкой пересечения делятся пополам, диагонали делят углы пополам.

Прямоугольный треугольник: катет, лежащий против угла в 30° равен половине гипотенузы.

Равнобедренный треугольник: две стороны равны, углы при основании равны.

Равнобедренная трапеция: две стороны равны, углы при основании равны.

Слайд 2

Молодцы! А для чего мы изучали все эти фигуры?

Правильно. На столе у вас листок с заданием. Я предлагаю вам, работая в группах, соотнеси фигуру с соответствующей формулой нахождения площади. Работу можно выполнять прямо на этом листке, соединив их стрелками.

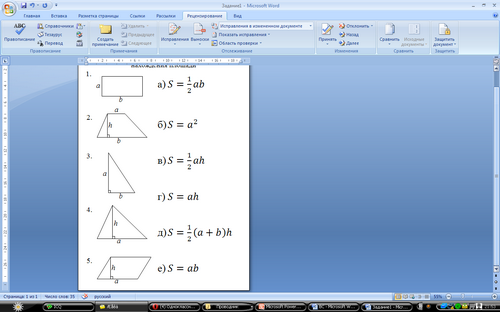
Хорошо, а какая формула оказалась лишней? Площадь какой фигуры находится по этой формуле?

Для того чтобы уметь находить их площадь.

Ребята, обсуждая в группе, соединяют каждую фигуру с соответствующей ей формулой.

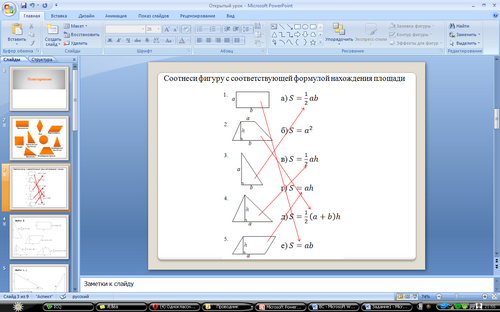
Лишняя формула под буквой «б», это формула нахождения площади квадрата.

Слайд 3

Молодцы! Формулы мы с вами повторили, а теперь давайте решим в группах следующие задачки на применение данных формул.

Найти: S

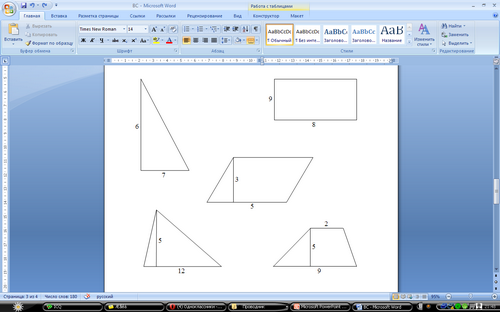
Работая в группах, записывают решения:

Прямоугольный треугольник: ;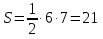

Прямоугольник: ;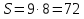

Параллелограмм: ;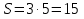

Треугольник: ;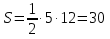

Трапеция: .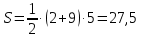

Слайд 4

Предложенное задание было простым, но бывает, что для решения сложных задач важна еще одна теорема. Посмотрите, пожалуйста, на слайд и скажите, на применение какой теоремы представлены эти задачи и решите их.

Найти: x, y

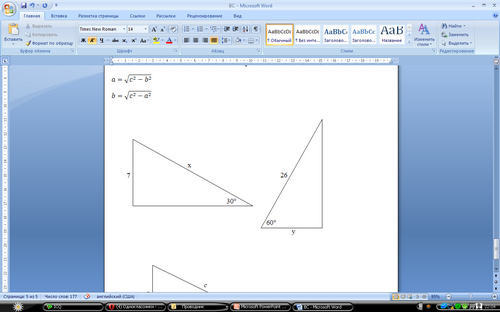
В прямоугольном треугольнике катет, лежащий против угла в 30° равен половине гипотенузы, поэтому: ; .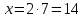

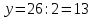Ответ: ; .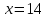

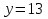Слайд 5

Молодцы! Также в геометрии очень важна и теорема Пифагора давайте вспомним ее.

Скажите как найти гипотенузу c, катеты a и b по этой теореме.

a

b

c

Квадрат гипотенузы равен сумме квадратов катетов.

;

;

.

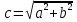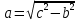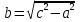Слайд 6

Теорему Пифагора мы повторили, а теперь давайте решим задачу на ее применение. Работаем в группах.

Найти: MK, MN

4

N

K

M

45°

Обсуждение в группах: Рассмотрим ∆MNK. Он прямоугольный и в нем 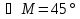, следовательно, 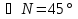. Поэтому ∆MNK - равнобедренный

.

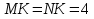Найдем MN по теореме Пифагора:

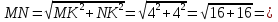
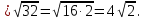
Ответ: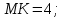

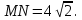
Слайд 7

Физкультминутка

Теперь немного отдохнем перед решением более сложной задачки на применение того, что мы уже с вами повторили.

Что изображено на картинке?

Сколько лиц?

Какие животные изображены?

Что изображено на картинке?

Двигаются ли зернышки? Стрелки?

Что вы видите?

Просмотр картинок с оптическими иллюзиями и стерео картинки.

Лошади, лев.

10.

Слон, лошадь, обезьяна, собака, кошка, мышка.

Карета, ребенок.

Нет.

Стрекозу.

Слайд 8-10

Формирование умений и навыков работы с задачей

Вот мы с вами и отдохнули немного, перейдем снова к работе. Предлагаю решить следующую задачу в группах. Она решается на основе материала, который мы с вами уже повторили.

Найти: AB, BE, S_ABCD

A

B

C

D

E

60°

4

5

Обсуждение в группах. Рассмотрим ∆ABE. Он прямоугольный и в нем 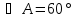, поэтому 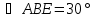. Следовательно, .

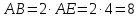Найдем BE по теореме Пифагора из ∆ABE:

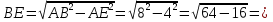
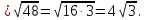
Тогда площадь параллелограмма будет равна:

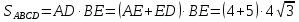
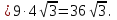
Ответ: ; ; .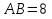

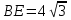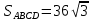Слайд 11

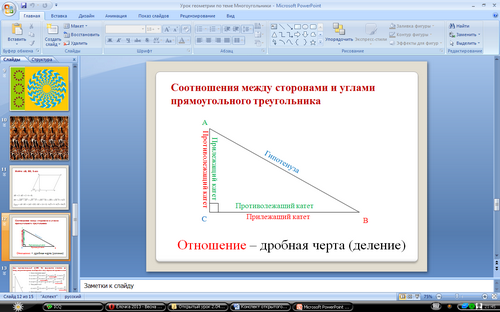
Молодцы! Последняя, очень важная тема, которую мы с вами изучили «Соотношения между сторонами и углами прямоугольного треугольника». С помощью нее можно решить многие задачи. Посмотрите на картинку и ответьте на следующие вопросы:

1. Как называется сторона, лежащая напротив прямого угла С.

2. Назовите прилежащий и противолежащий катет к углу А.

3. Назовите прилежащий и противолежащий катет к углу В.

4. Скажите, что такое синус, косинус и тангенс острого угла прямоугольного треугольника.

Ответы:

1. Гипотенуза.

2. Прилежащий - АС, противолежащий ВС.

3. Прилежащий - ВС, противолежащий АС.

4. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Слайд 12

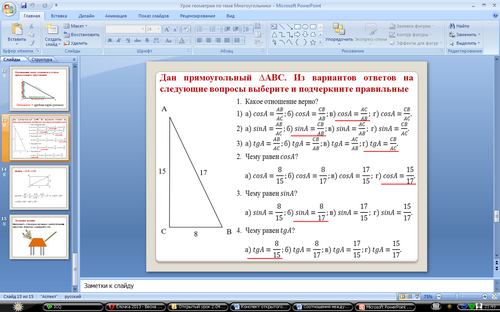
Молодцы! Теперь мы все повторили для того, чтобы выполнить следующее задание. На столе у вас листок с заданием. Дан прямоугольный ∆АВС. Из вариантов ответов на следующие вопросы выберите и подчеркните правильные. Работаем в группах. Работу можно выполнять прямо на этом листке, подчеркивая соответствующий вариант ответа.

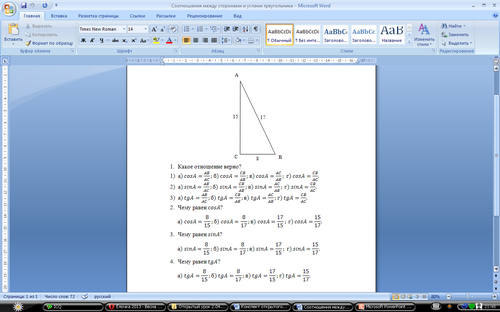
Обсуждение в группах.

Слайд 13

Ну и последнее задание, которое нам предстоит сегодня на уроке выполнить. Работаем в группах.

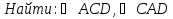
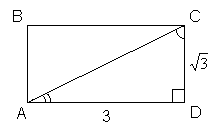
Обсуждение в группах. Рассмотрим прямоугольный ∆ACD. В нем известны катеты, поэтому можно воспользоваться определением тангенса. Например,

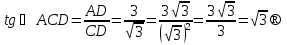
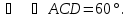
Второй угол найдем через сумму острых углов прямоугольного треугольника, т.е.

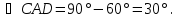
Ответ: ,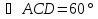

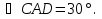
Слайд 14

Подведение итогов работы на уроке

Подведем итог. Чем сегодня мы занимались на уроке? Был ли он для вас полезным?

На уроке мы повторяли и систематизировали знания по теме «Многоугольники». Урок был полезен тем, что мы все вспомнили и привели знания в систему.

Задание на дом

Молодцы, вы сегодня хорошо поработали. Поэтому я предлагаю дома вам выполнить следующее творческое задание, а именно нарисовать с помощью изученных многоугольников известное животное и раскрасить его. Например:

Спасибо за урок! Вы можете быть свободными.

Слушают домашнее задание и записывают его в дневник.

Слайд 15