Тема урока: Окружность и ее элементы. Центральные углы

Тема урока: Окружность и ее элементы. Центральные углы

Цель урока: усвоение новых знаний об окружности и её элементах, о центральных углах

Задачи урока: научиться строить окружность, находить радиус, если известен диаметр, и, наоборот, диаметр, если известен радиус, логически и пространственное мыслить

Ход урока:

1 этап: Орг момент, приветствие, проверка домашнего задания

2 этап: Новая тема:

Определение: Множество точек плоскости, равноудаленных от данной точки, называется окружностью. Данная точка О - называется центром окружности. Для построения окружности используют циркуль.

Определение: Отрезок, соединяющий центр с какой- либо точкой окружности, называется радиусом окружности. ОА = ОВ = ОС = ОD = r - радиусы Обозначение окружности с центром в точке О и радиусом r. Точки А, В, С, D делят окружность на части, которые называются дугами. АВ, и т.д. - знак дуги.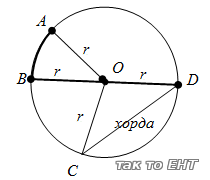

Определение: Отрезок, соединяющий две любые точки окружности, называется её хордой. CD - хорда

Определение: Хорда, проходящая через центр окружности, называется её диаметром. BD - диаметр, BD = d. BD = BO + OD = r + r = 2r. d = 2r.

Две окружности равны, если равны их радиусы. При наложении центров друг на друга окружности совпадут.

Определение.

Касательная к окружности - это прямая, которая имеет с окружностью только одну общую точку - точку касания.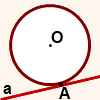

a - касательная,

A - точка касания

Центральный угол - это угол, вершина которого лежит в центре окружности, а стороны пересекают окружность.

Стороны центрального угла делят окружность</ на две дуги. Одна из дуг лежит внутри центрального угла, другая - вне его.

Когда говорят, что центральный угол опирается на дугу, то имеют в виду внутреннюю дугу, лежащую между сторонами угла.

Например, на рисунке 1 ∠AOC - центральный. Его вершина - точка O - центр окружности.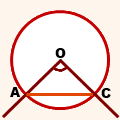

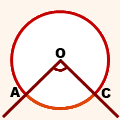
Стороны - лучи OA и OC - пересекают окружность. Вписанный угол AOC опирается на дугу AC. Также говорят, что центральный угол опирается на хорду. В этом случае речь идет о хорде, соединяющей точки пересечения сторон центрального угла с окружностью.

Например на рисунке 2 центральный угол АОС опирается на хорду АС. Говорят, что хорду АС видно из центра окружности под углом АОС

3 этап: решение задач у доски:

№ 206

Радиус окружности равен 2,5 см. Найдите ее диаметр. Может ли ее хорда иметь 6 см?

Решение: d= 2r d=2,5*2=5 не может, так самая длинная хорда - это и есть диаметр. Диаметр равен 5 см, значит хорда не может быть равна 6 см

№ 209 Дана окружность с центром О. Точка А является внутренней точкой этой окружности. В скольких точках пересекает окружность:1)прямая ОА,2)луч ОА,3)отрезок ОА

Решение: 1)в двух 2)в одной 3) не пересекает