Справочник к уроку геометрии для 11 кл Примеры решения стереометрических задач

Здравствуйте, Дорогие друзья! Продолжаем рассматривать задачи с пирамидами. На блоге уже рассмотрены задания с правильными пирамидами, в этих статьях шла речь о нахождении элементов и площади поверхности. Здесь разберём примеры связанные с понятием объёма. Для решения подобных заданий обязательно нужно знать - формулу объёма пирамиды:

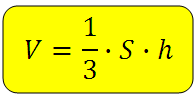
S - площадь основания пирамиды

h - высота пирамиды

Основанием может быть любой многоугольник. Но в большинстве задач на ЕГЭ речь в условии, как правило, идёт о правильных пирамидах. Напомню одно из её свойств:

Вершина правильной пирамиды проецируется в центр её основания

Посмотрите на проекцию правильной треугольной, четырёхугольной и шестиугольной пирамид (ВИД СВЕРХУ):

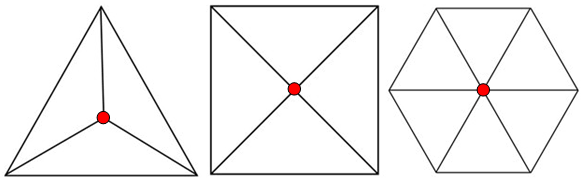
Можете посмотреть ещё одну статью</</u> на блоге, где разбирались задачи связанные с нахождением объёма пирамиды.

Рассмотрим задачи:

27087. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна корню из трёх.

Объём пирамиды вычисляется по формуле:

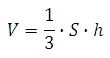
S - площадь основания пирамиды

h - высота пирамиды

Найдём площадь основания пирамиды, это правильный треугольник. Воспользуемся формулой - площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Таким образом, объём пирамиды равен:

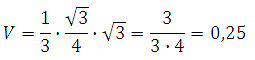
Ответ: 0,25

27088. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен корню из трёх.

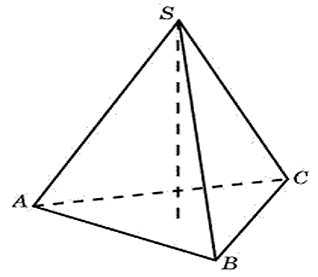
Такие понятия как высота пирамиды и характеристики её основания связаны формулой объёма:

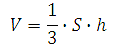
S - площадь основания пирамиды

h - высота пирамиды

Сам объём нам известен, площадь основания можем найти, так как известны стороны треугольника, который является основанием. Зная указанные величины без труда найдём высоту.

Для нахождения площади основания воспользуемся формулой - площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Таким образом, подставив данные значения в формулу объема можем вычислить высоту пирамиды:

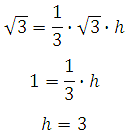
Высота равна трём.

Ответ: 3

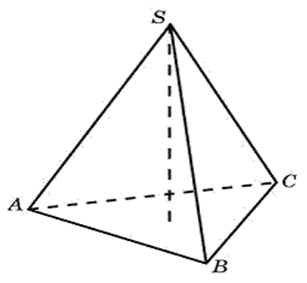
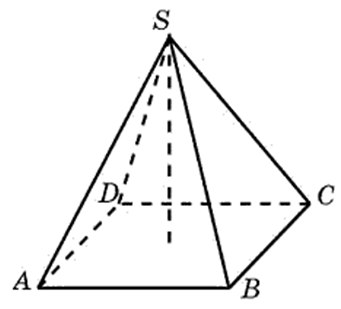
27109. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

Объём пирамиды вычисляется по формуле:

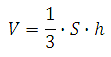
S - площадь основания пирамиды

h - высота пирамиды

Высота нам известна. Необходимо найти площадь основания. Напомню, что вершина правильной пирамиды проецируется в центр её основания. Основанием правильной четырёхугольной пирамиды является квадрат. Мы можем найти его диагональ. Рассмотрим прямоугольный треугольник (выделен синим):

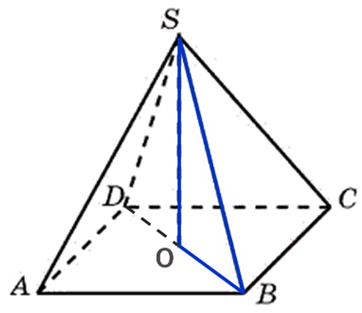
Отрезок соединяющий центр квадрата с точкой В это катет, который равен половине диагонали квадрата. Этот катет можем вычислить по теореме Пифагора:

Значит BD = 16. Вычислим площадь квадрата воспользовавшись формулой площади четырёхугольника:

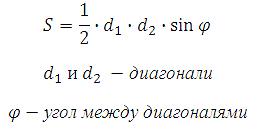
Следовательно:

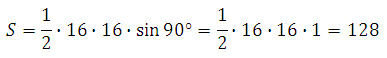
Таким образом, объём пирамиды равен:

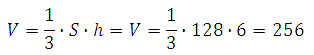
Ответ: 256

27178. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

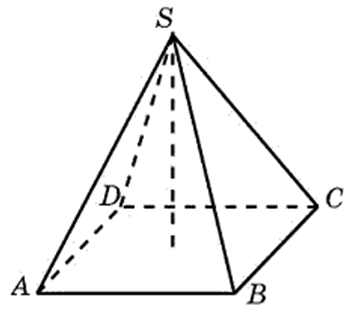
Высота пирамиды и её и объём известны, значит можем найти площадь квадрата, который является основанием. Зная площадь квадрата, мы сможем найти его диагональ. Далее рассмотрев прямоугольный треугольник по теореме Пифагора вычислим боковое ребро:

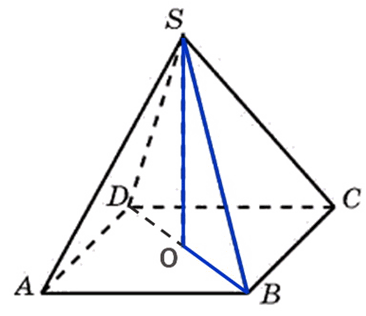
Найдём площадь квадрата (основания пирамиды):

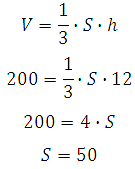
Вычислим диагональ квадрата. Так как его площадь равна 50, то сторона будет равна корню из пятидесяти и по теореме Пифагора:

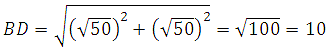
Точка О делит диагональ BD пополам, значит катет прямоугольного треугольника ОВ = 5.

Таким образом, можем вычислить чему равно боковое ребро пирамиды:

Ответ: 13

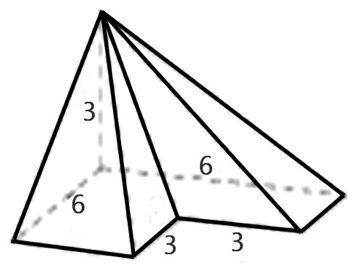
245353. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

Как уже неоднократно было сказано - объём пирамиды вычисляется по формуле:

S - площадь основания пирамиды

h - высота пирамиды

Боковое ребро перпендикулярное основанию равно трём, это означает, что высота пирамиды равна трём. Основания пирамиды - это многоугольник, площадь которого равна:

Таким образом:

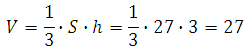
Ответ: 27