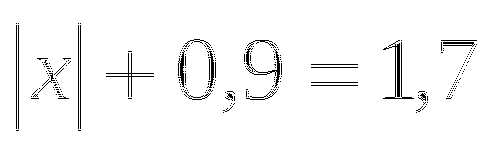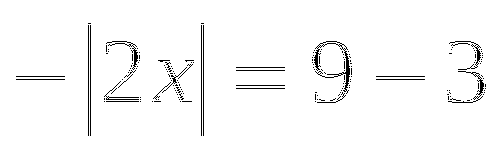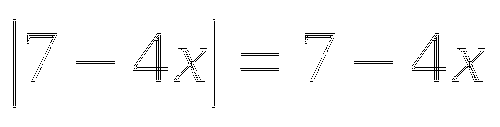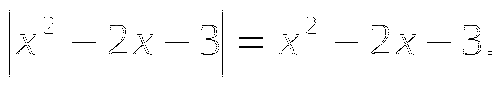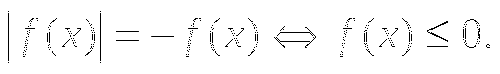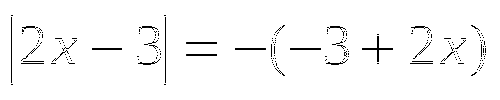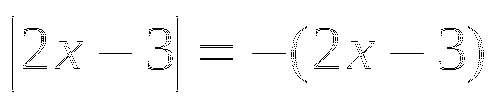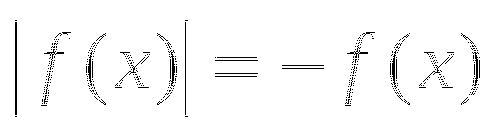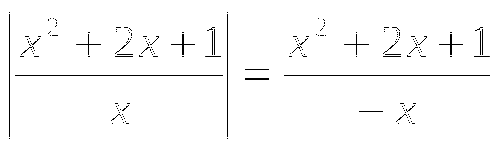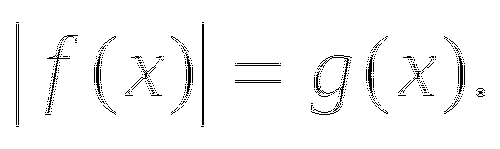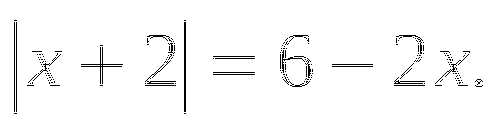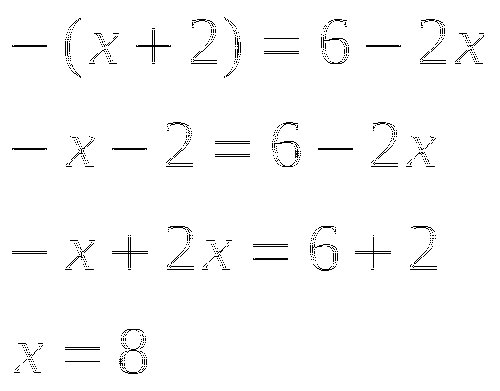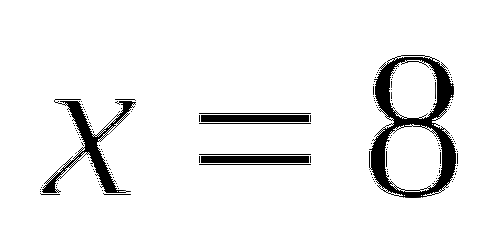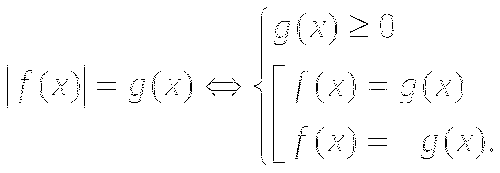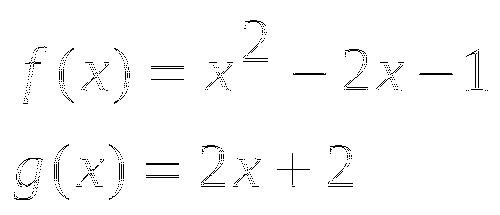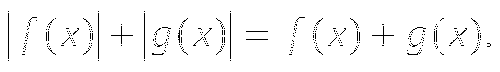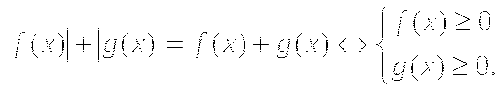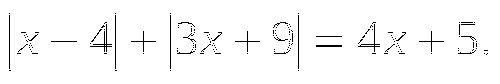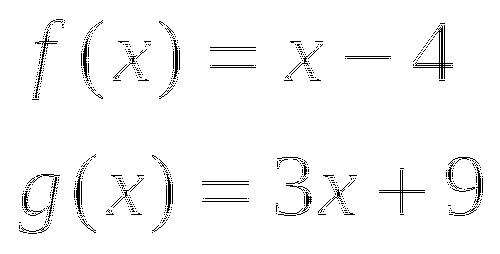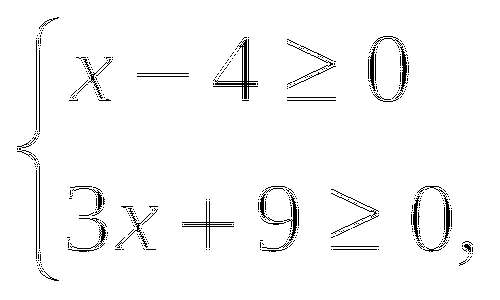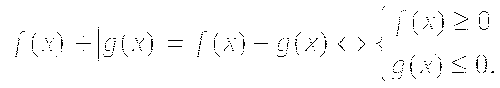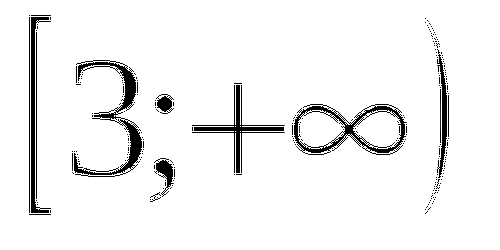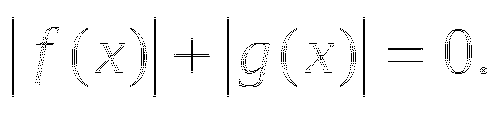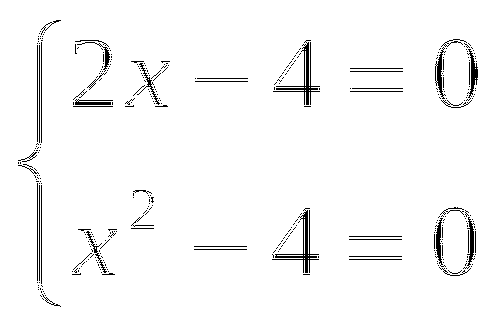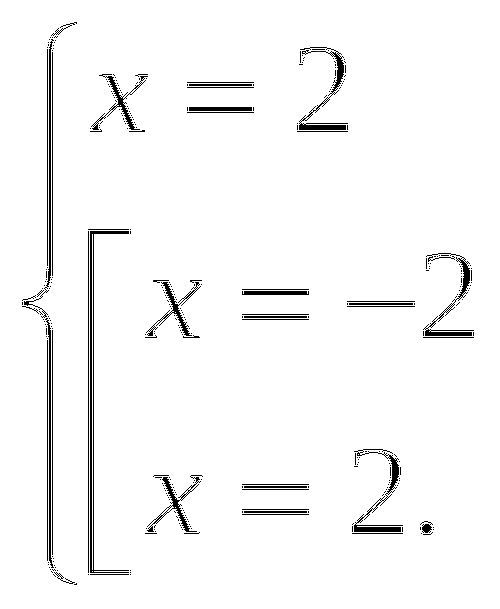- Учителю
- Статья по математике на тему 'УРАВНЕНИЯ, СОДЕРЖАЩИЕ МОДУЛИ. ИСПОЛЬЗОВАНИЕ РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ'
Статья по математике на тему 'УРАВНЕНИЯ, СОДЕРЖАЩИЕ МОДУЛИ. ИСПОЛЬЗОВАНИЕ РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ'
Автор публикации: Гильмиева Г.Г.
Дата публикации: 27.04.2015
Краткое описание: Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа, как в области действительных чисел, так и в области комплексных чисел. Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей ма
предварительный просмотр материала
Уравнения, содержащие модули.
Использование равносильных преобразований
1.1. Уравнение вида ![]()
Рассмотрим простейшее уравнение вида:
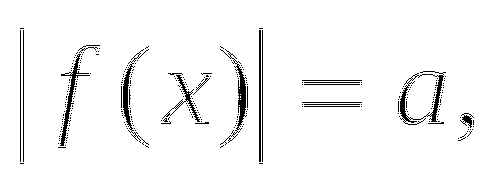 где
где 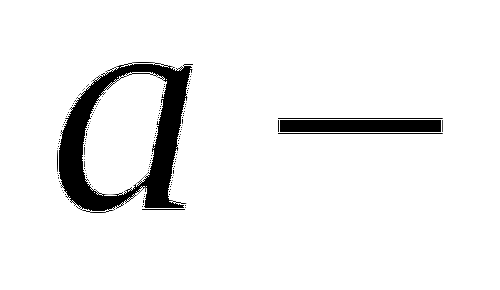 число.
число.
Если  то решений нет.
то решений нет.
Если 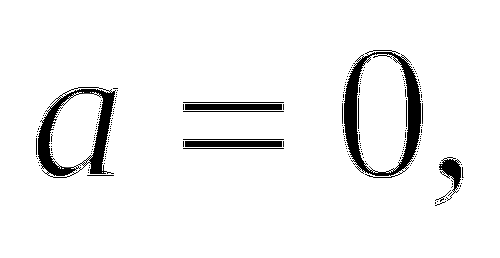 то
то 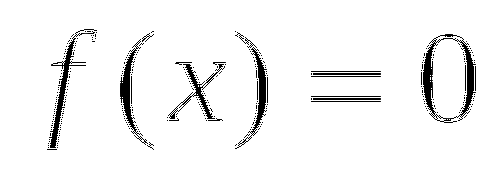 .
.
Если 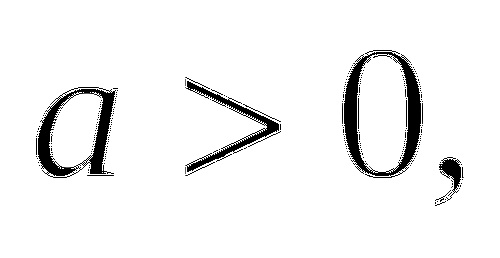 то
то 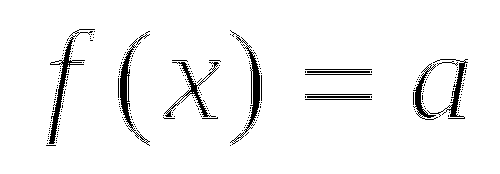 или
или 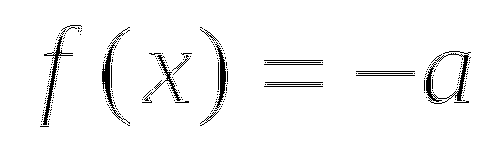 .
.
Примеры.
Решите уравнения:
а) 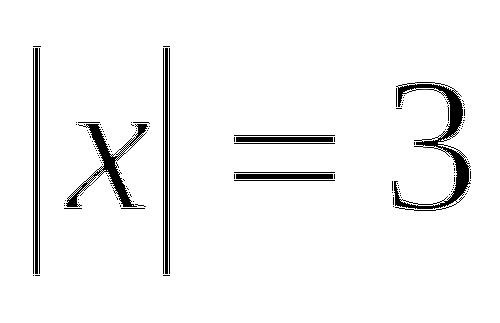
б) 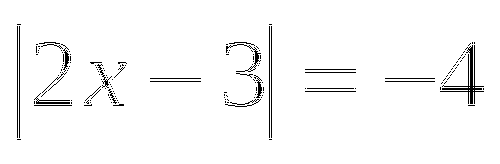
в) 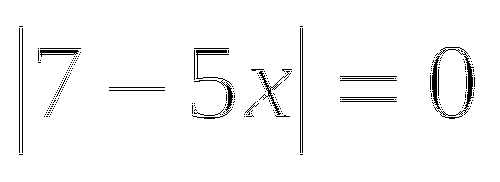
г) 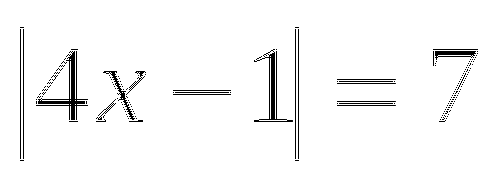
д) 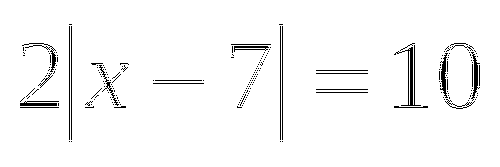
е) 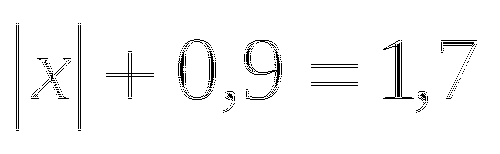
ж) 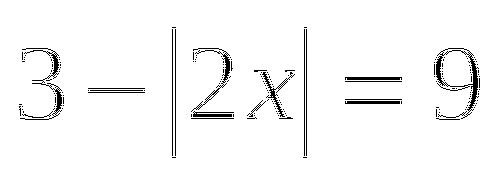
Решение:
а) 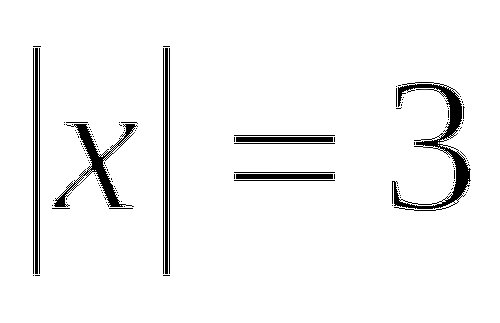
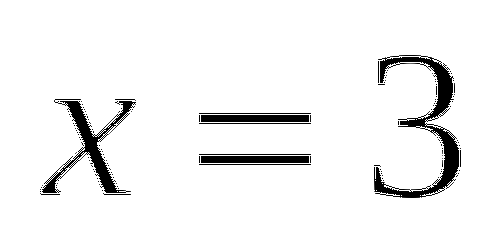 или
или 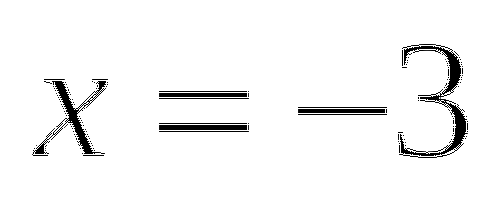 .
.
б) 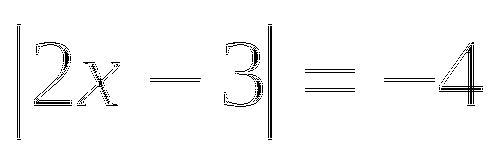
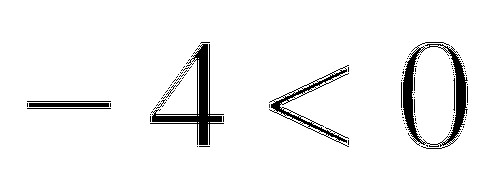 , то уравнение решений не имеет.
, то уравнение решений не имеет.
в) 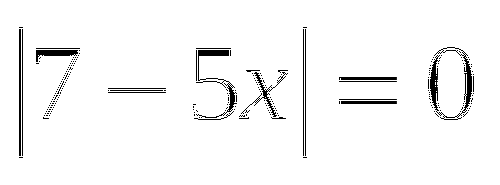
г) 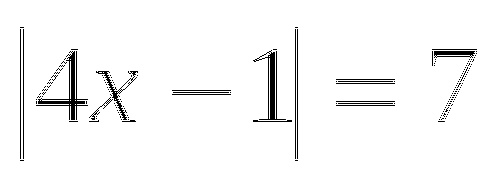
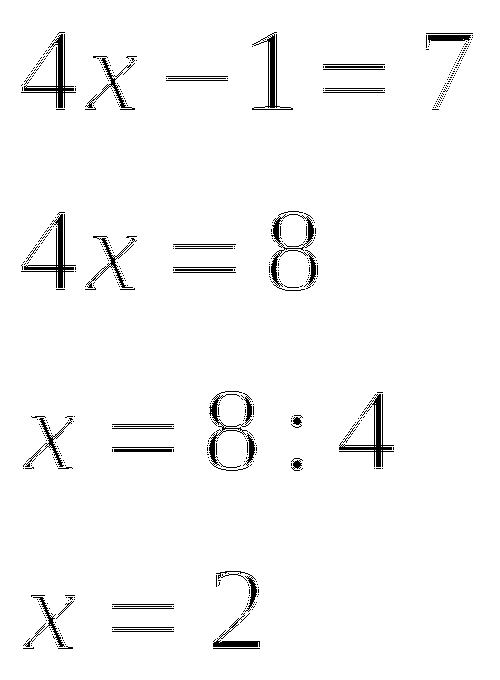 или
или 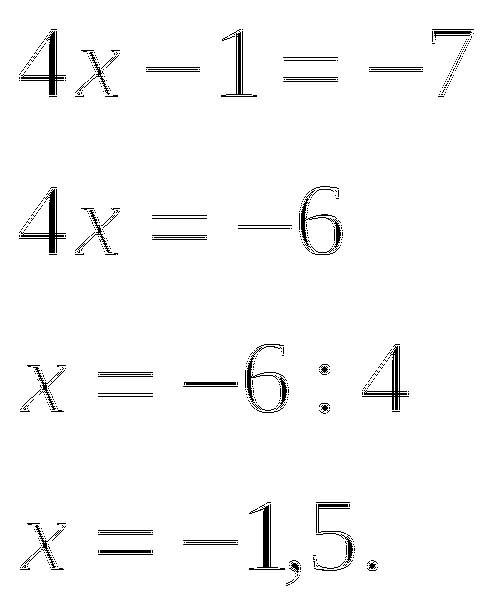
д) 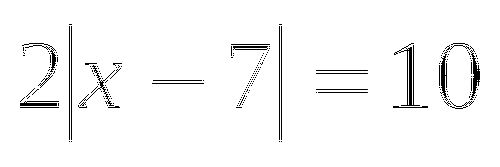
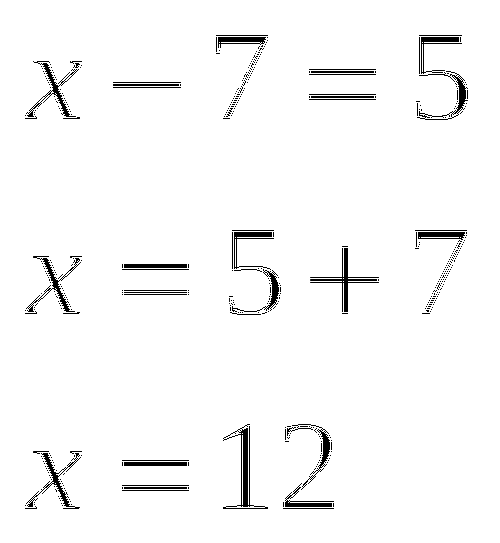 или
или 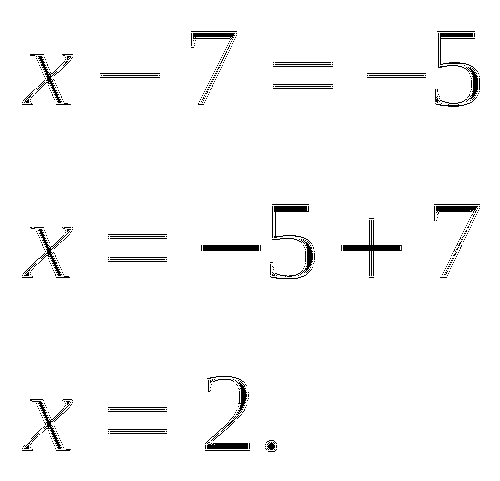
е) 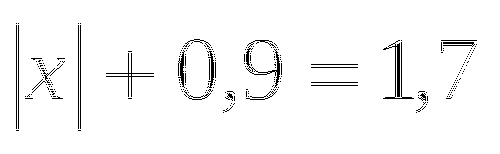
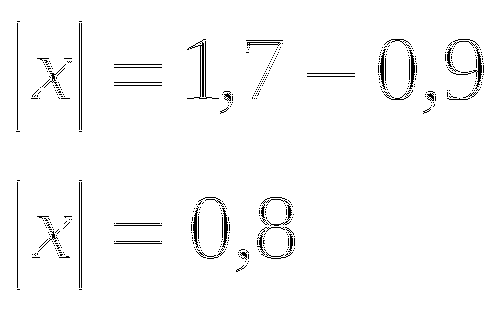 или
или 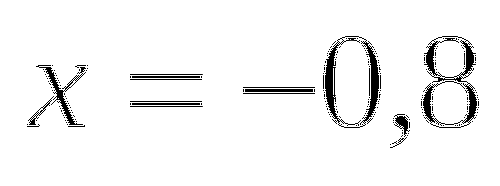
ж) 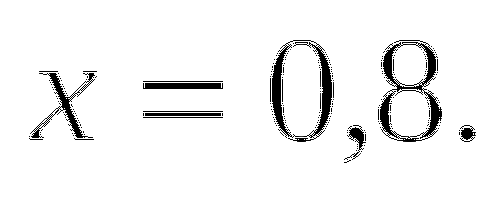
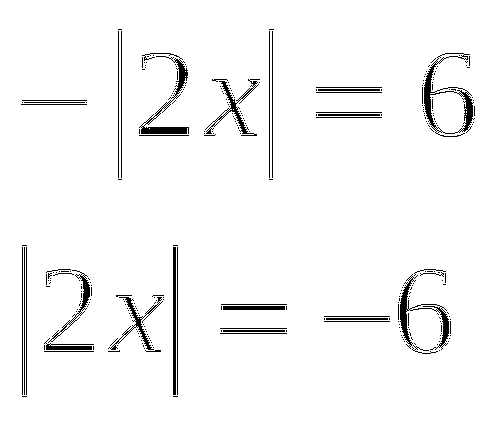 нет решений.
нет решений.
Ответ: а) 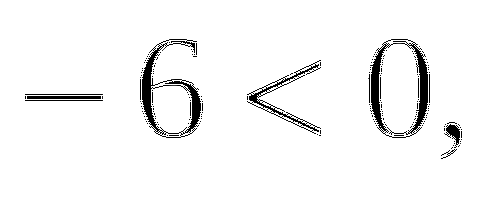
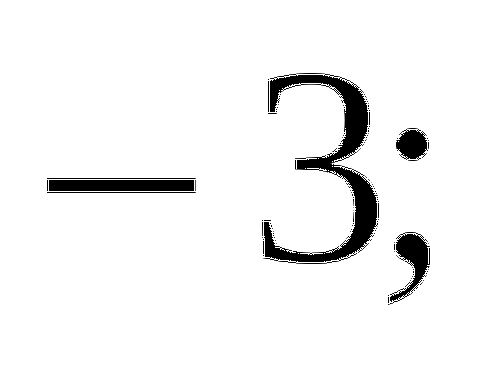
б) нет решений
в) 1,4
г) 
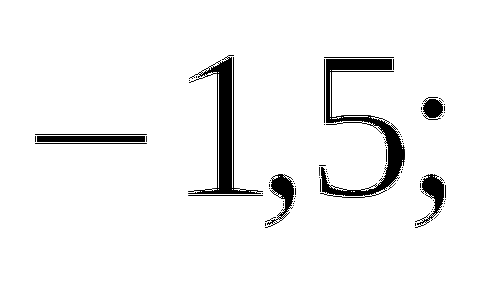
д) 2; 12
е) 
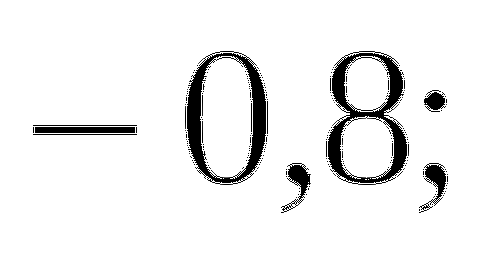
ж) нет решений
1.2. Уравнение вида ![]()
Примеры.
Решите уравнения:
а) 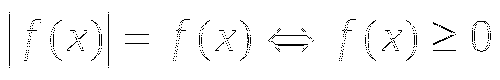
б) 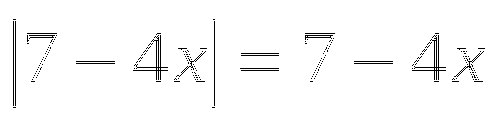
Решение:
а) 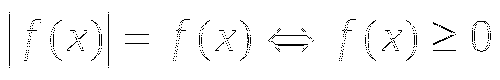
б) 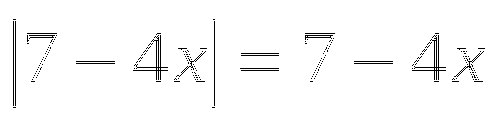
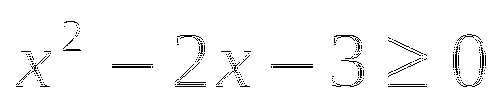 или
или 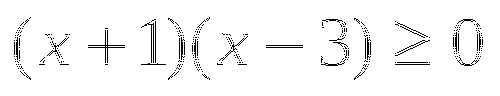
Ответ: а) 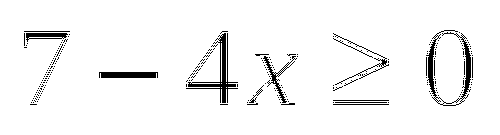
б) 
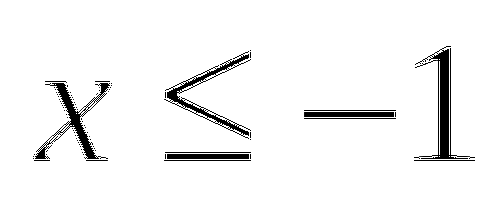
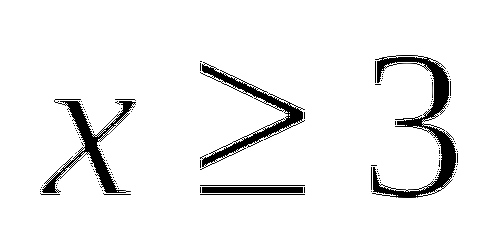 .
.
1.3. Уравнение вида ![]()
Примеры.
Решите уравнения:
а) 
б) 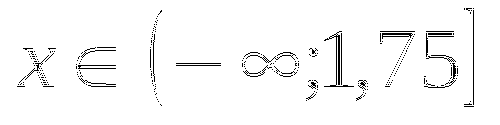 .
.
Решение:
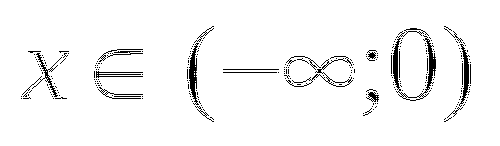
а) 
Запишем уравнение в виде 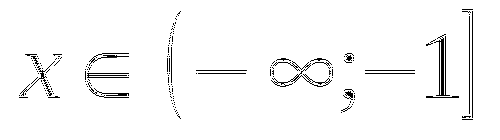 ,
,
Получили уравнение вида
Оно равносильно неравенству:
Данное уравнение можно было бы решить иначе, используя свойство модуля: 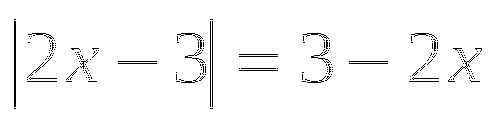
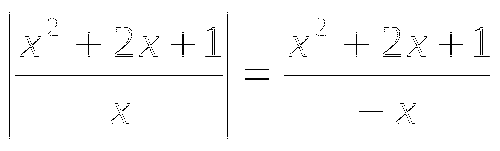 тогда уравнение примет вид:
тогда уравнение примет вид:
Получили уравнение вида 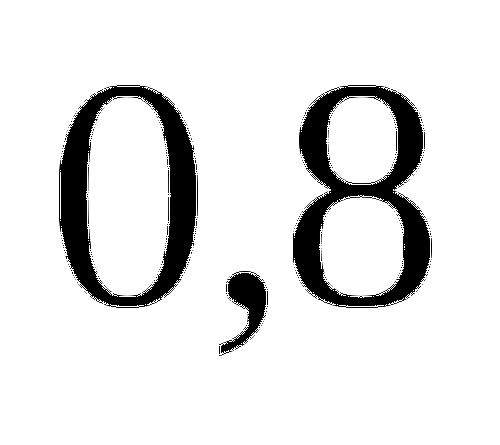
б) 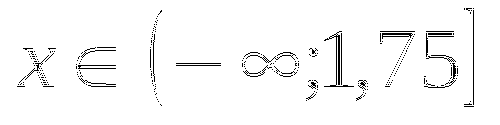
Уравнение равносильно неравенству
Ответ: а) 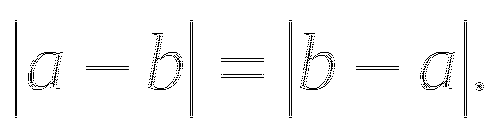
б) 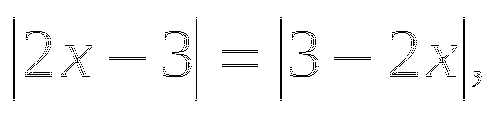
1.4. Уравнение вида ![]()
Рассмотрим уравнение:
Решение:
Большое количество ошибок при решении задач этого типа вызвано тем, что учащиеся, освобождаясь от модуля, забывают учесть условия, при которых модуль был раскрыт с тем или иным знаком.
Рассмотрим первый случай, когда 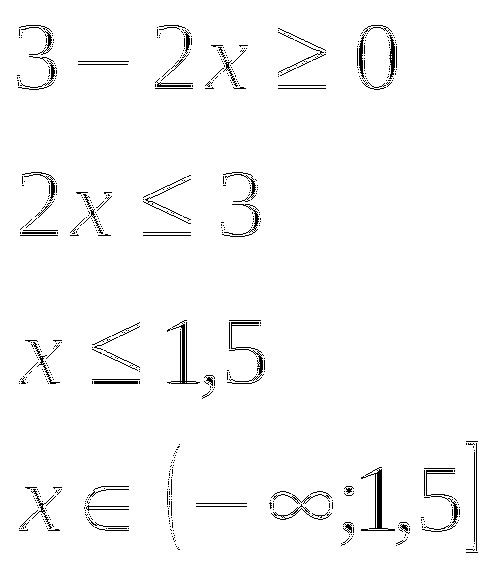 Тогда модуль в левой части уравнения раскрывается со знаком «+», то есть уравнение примет вид:
Тогда модуль в левой части уравнения раскрывается со знаком «+», то есть уравнение примет вид:
Поскольку 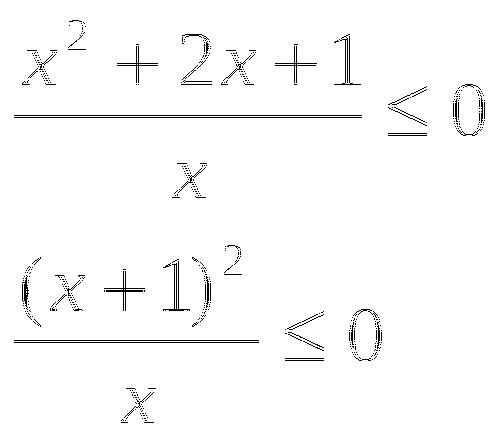 (верно), то значение
(верно), то значение 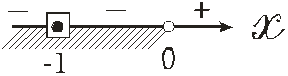 является корнем данного уравнения.
является корнем данного уравнения.
Во втором случае 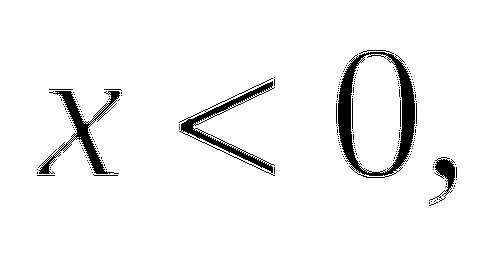 . Тогда модуль раскрывается со знаком «-», и исходное уравнение переписывается в виде:
. Тогда модуль раскрывается со знаком «-», и исходное уравнение переписывается в виде:
Поскольку значение 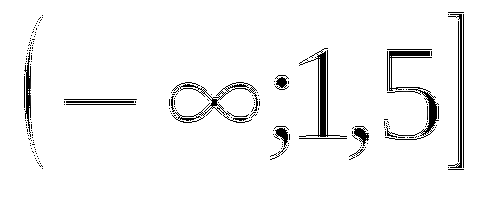 не удовлетворяет условию
не удовлетворяет условию 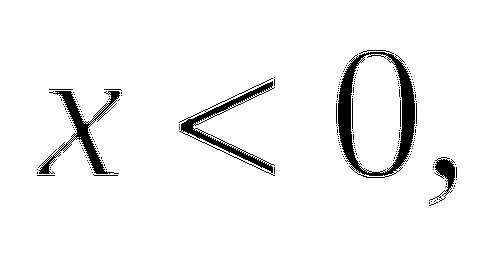 (8+2=10, 10<0 неверно), то оно не является корнем уравнения.
(8+2=10, 10<0 неверно), то оно не является корнем уравнения.
Ответ:  .
.
Уравнение вида 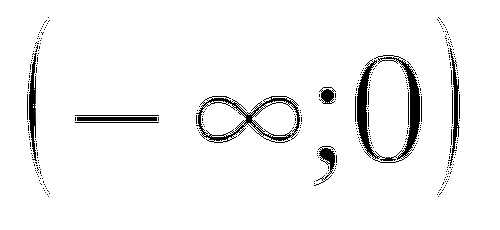 можно решать двумя способами. Первый, стандартный, основан на раскрытии модуля, исходя из его определения, и заключается в переходе к совокупности (объединению) двух систем:
можно решать двумя способами. Первый, стандартный, основан на раскрытии модуля, исходя из его определения, и заключается в переходе к совокупности (объединению) двух систем:
Именно этим способом был решен выше приведенный пример.
Второй способ состоит в переходе от исходного уравнения к равносильной системе:
Первый способ рациональнее применять в случае сложного выражения для функции 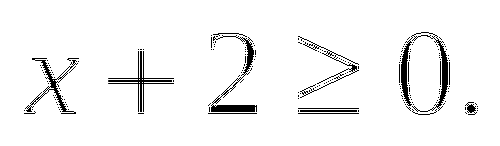 и не очень сложного для функции
и не очень сложного для функции 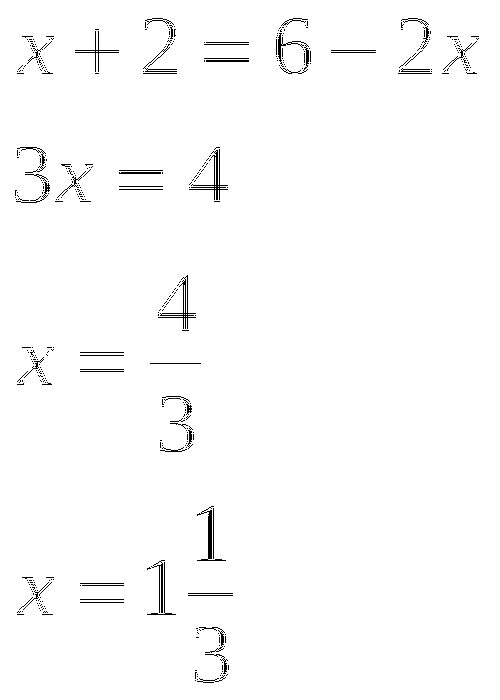 Второй способ удобнее использовать, если выражение для функции
Второй способ удобнее использовать, если выражение для функции 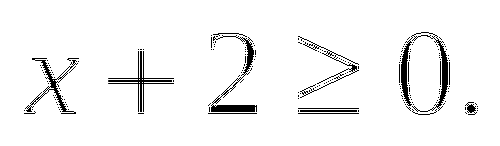 не сложно.
не сложно.
Пример.
Решите уравнение:
Решение:
В нашем случае 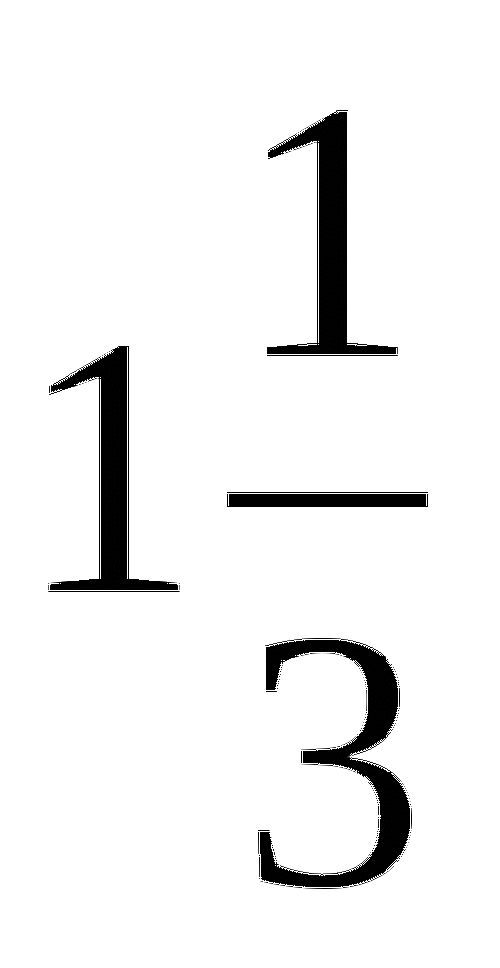
Выражение для функции 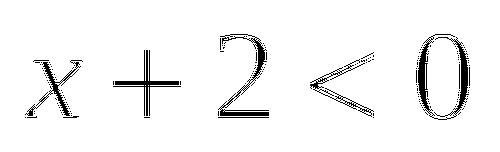 «проще», используем второй способ решения. Для этого запишем систему, равносильную исходному уравнению:
«проще», используем второй способ решения. Для этого запишем систему, равносильную исходному уравнению:
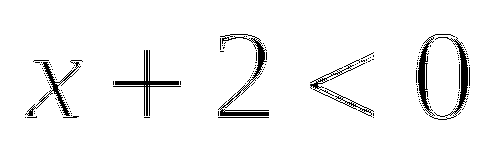 имеет корни
имеет корни 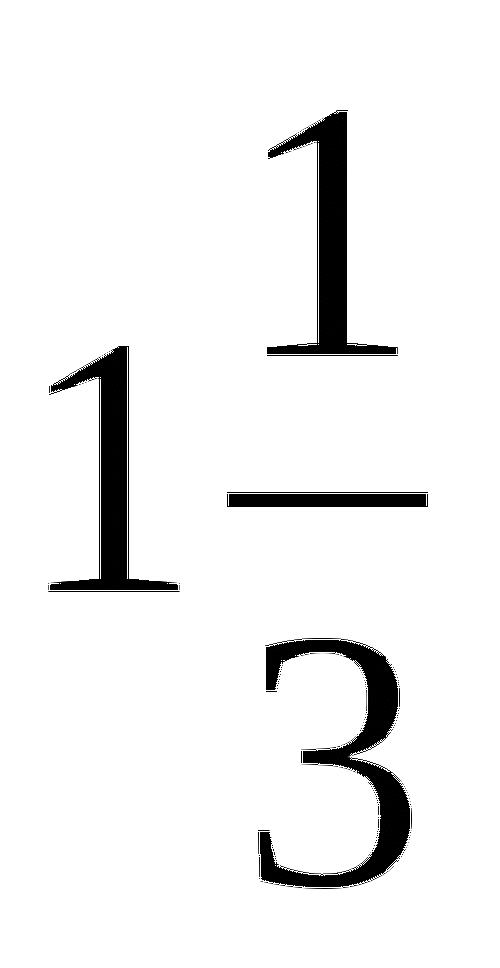
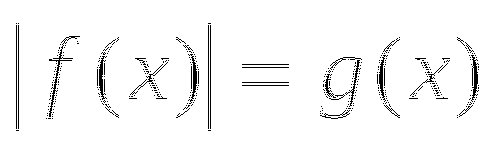
Уравнение 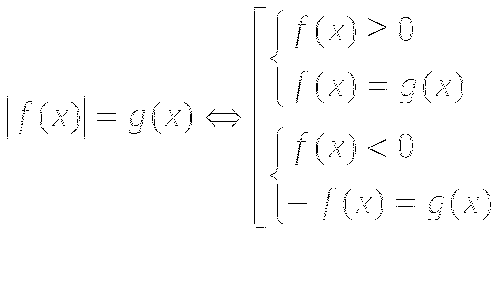 решений не имеет.
решений не имеет.
Оба корня удовлетворяют неравенству 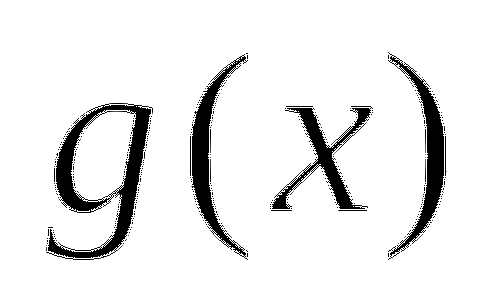
Ответ: 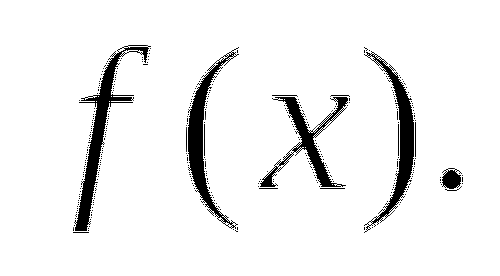
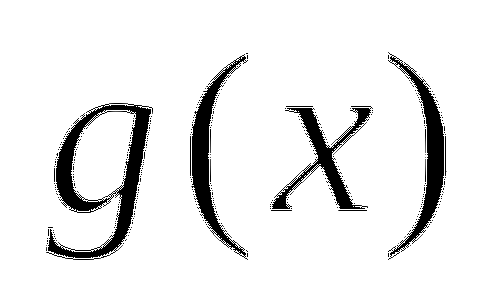
Решив уравнение первым способом, можно убедиться, что в этом случае он менее рационален.
1.5. Уравнение вида ![]()
Пример.
Решите уравнение:
Решение:
В нашем случае 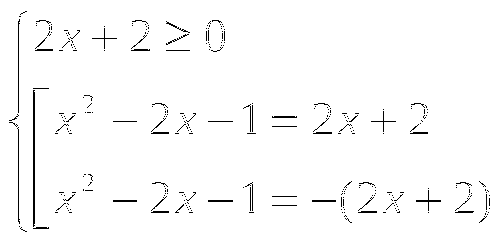
Тогда исходное уравнение будет равносильно системе:
Ответ: 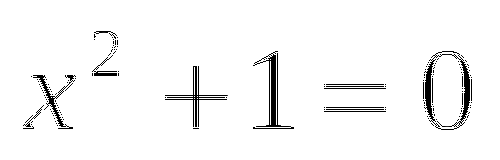
1.6. Уравнение вида ![]()
Пример.
Решите уравнение:
Решение:
Заметим, что 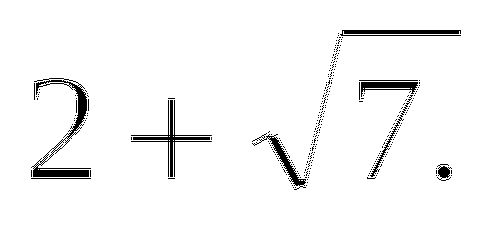
Тогда уравнение будет равносильно системе:
Ответ: 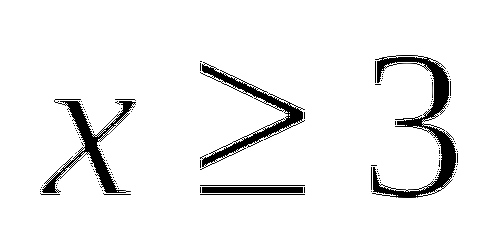
1.7. Уравнение вида ![]()
Пример.
Решите уравнение:
Решение:
Так как 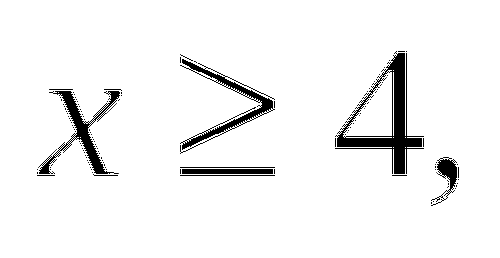
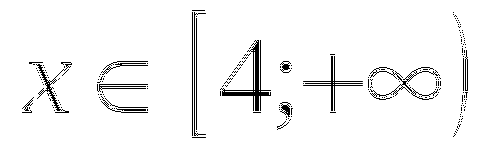 при любых
при любых 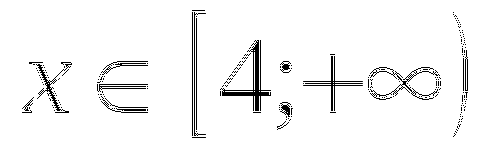 , то исходное уравнение равносильно системе
, то исходное уравнение равносильно системе
Ответ: 2.
Полезно знать, что 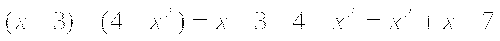
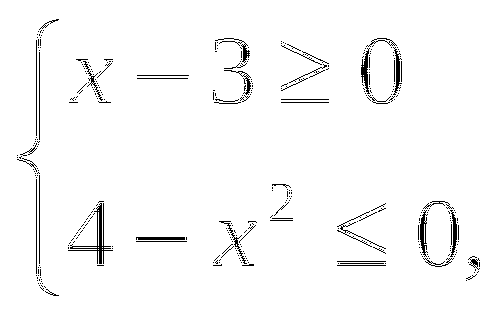
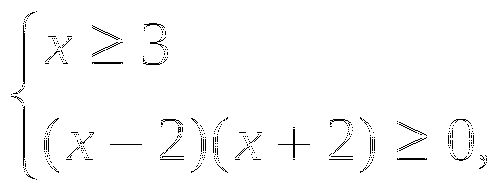
Покажем, как можно решить уравнение 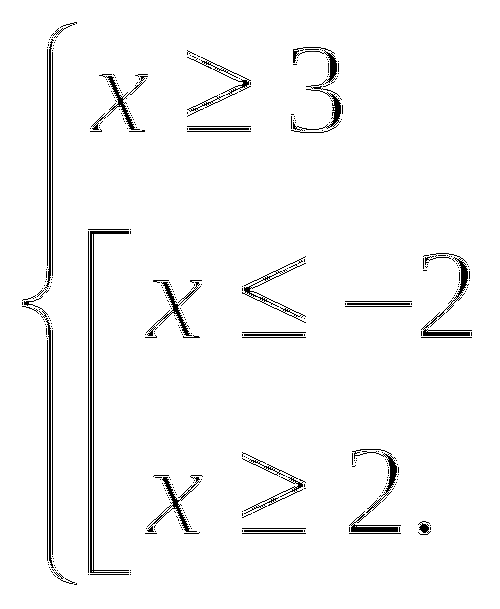 Перейдем к равносильной системе уравнений:
Перейдем к равносильной системе уравнений:
Ответ: 0.
1.8. Уравнение вида ![]()
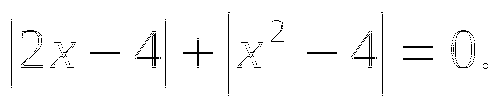 .
.
Пример.
Решите уравнение:
Решение:
В нашем случае 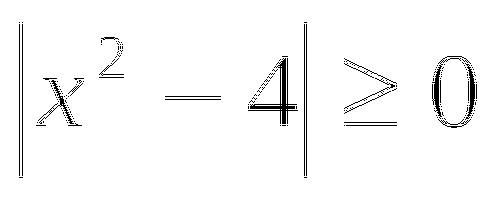
 .
.
Уравнение будет равносильно неравенству:
Ответ: 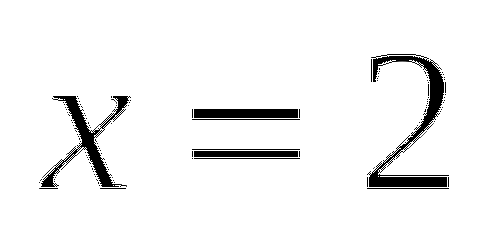
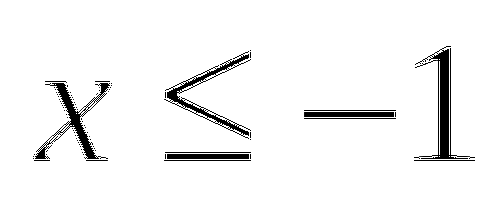
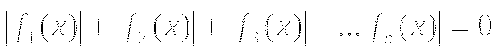
1.9. Уравнение вида ![]() .
.
Пример.
Решите уравнение:
Решение:
Уравнение равносильно неравенству:
Разделим обе части неравенства на 6
Ответ: 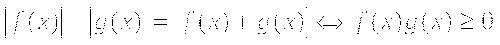
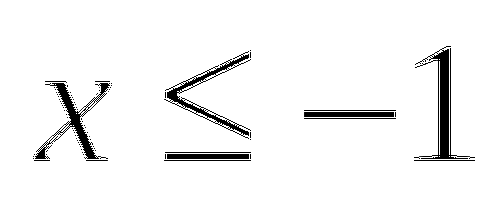
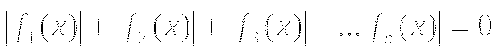
1.10. Уравнение вида ![]() .
.
Уравнение 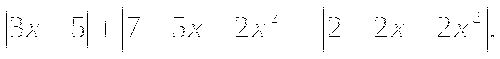 равносильно объединению уравнений:
равносильно объединению уравнений:
Примеры.
Решите уравнения:
а) 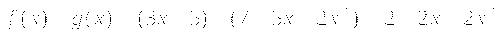
б) 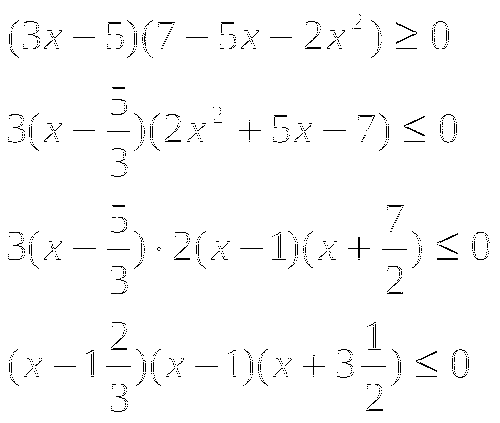
Решение:
а) 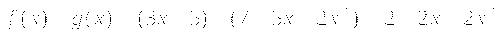
б) 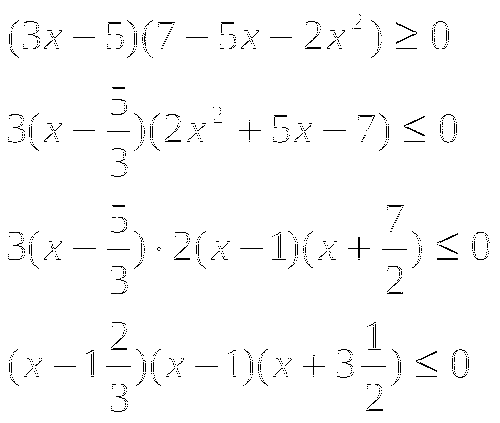
Решим каждое уравнение совокупности:
Первое уравнение имеет корни 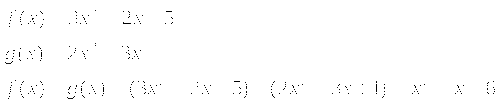
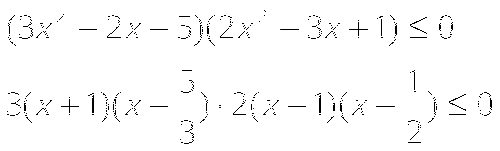 .
.
Для второго уравнения найдем дискриминант D=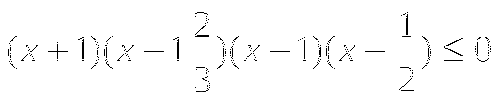
Его корни 
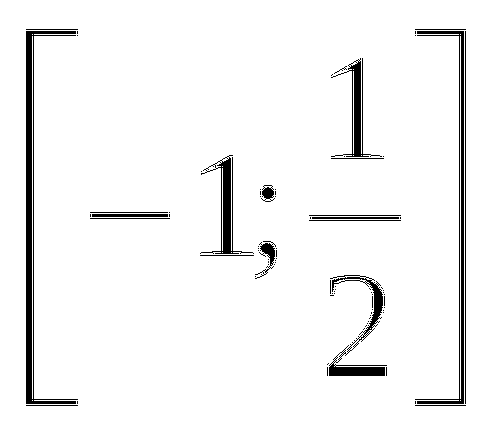
Ответ: а) 0; 1
б)  1;
1; 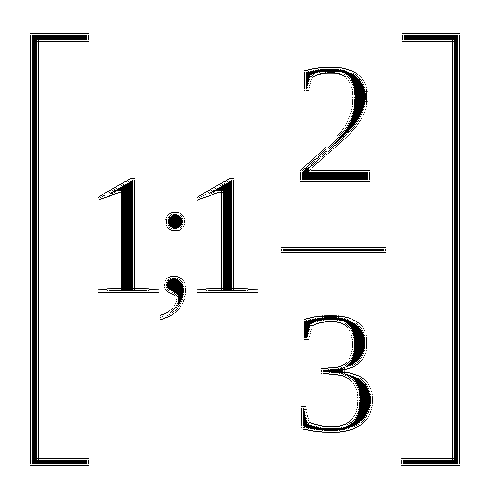 6
6