Конспект урока по алгебре и началам математического анализа на тему ' Уравнения, сводящиеся к простейшим заменой неизвестного ' (10 класс)

УРОК № 3 Тема 6. Показательные и логарифмические уравнения и неравенства (11ч)

Тема урока. Уравнения, сводящиеся к простейшим заменой неизвестного.

Цель урока: Сформировать навыки решения показательных уравнений, способом приведения к одинаковому основанию и уравнений, сводящиеся к простейшим, заменой неизвестного.

Тип урока: комбинированный.

Ход урока

1. Организационный момент.

2. Проверка домашнего задания.

3. Актуализация опорных знаний.

1. Какие уравнения называются показательными?

2. Объясните, в каких случаях показательное уравнение a^x=b (где a>0 и a≠1) имеет корни. В каких случаях это уравнение не имеет корней?

4. Объяснение нового материала и его поэтапное закрепление.

1.1. Объяснение нового материала.

Решите уравнение: ,

,

2х - 7 = 2,

х = 4,5.

Ответ: 4,5.

1.2. Поэтапное закрепление.

№ 6.16(в,г). Решите уравнения. № 6.17(д). Решите уравнения.

в) , г) , д) ,

, , ,

-3х + 1 = 4, х - 6 = -2, х² + х - 2 = 0,

х = -1. х = 4. х₁ = 1, х₂ = -2.

Ответ: -1. Ответ: 4. Ответ: -2; 1.

Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?

2.1. Объяснение нового материала.

Решите уравнение: ,

,

Пусть ,

,

a + b + c = 0, то

t₁ = 1, t₂ = 2,

, ,

, ,

х₁ = 0. х₂ = 1. Ответ: 0; 1.

2.2. Поэтапное закрепление.

№ 6.21(а,в). Решите уравнения.

а) ,

,

Пусть ,

,

t₁ = 2, t₂ = 3,

, ,

, х₂ = 1. Ответ: ; 1.

в) ,

Пусть ,

,

a - b + c = 0, то

t₁ = - 1 - не удовлетворяет условию замены,

t₂ = 3,

,

х = 0,5. Ответ: 0,5.

Вывод: Какой способ решения такого типа уравнений необходимо примен Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?ить? Почему?

3.1. Объяснение нового материала.

Решите уравнение: ,

,

,

,

,

,

,

4х² - 8х + 3 = 0,

, ,

,

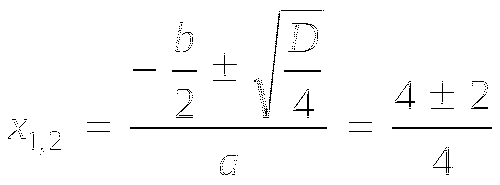х₁ = 0,5. х₂ = 1,5. Ответ: 0,5; 1,5.

3.2. Поэтапное закрепление.

№ 6.19(а,в). Решите уравнения.

а) ,

,

,

Пусть ,

,

, ,

,

t₁ = . t ₂ = 3.

,

,

,

, , то корней нет.

,

,

,

х(2х - 3) = 0,

х₁ = 0. х₂ = 1,5. Ответ: 0; 1,5.

в) ,

,

,

Пусть ,

,

a + b + c = 0, то

t₁ = 1. t ₂ = -1,5 - не удовлетворяет условию замены.

,

,

, ,

,

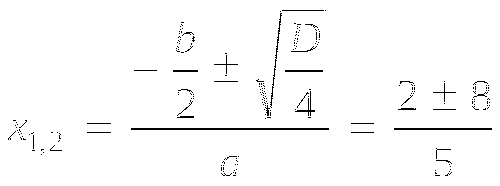х₁ = -1,2. х₂ = 2. Ответ: -1,2; 2.

Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?

4.1. Объяснение нового материала.

Решите уравнение: ,

,

,

Пусть ,

, ОДЗ: t  0,

,

a + b + c = 0, то

t₁ = 1. t ₂ = 4,

, ,

, ,

х₁ = 0. х₂ = 2. Ответ: 0; 2.

4.2. Поэтапное закрепление.

№ 6.23(б). Решите уравнения.

б) ,

,

Пусть ,

, ОДЗ: t  0,

,

t₁ = 2, t ₂ = 7,

, ,

, х = 1. Ответ: ; 1.

Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?

5.1. Объяснение нового материала.

Решите уравнение: ,

Пусть

, ОДЗ: t  -2; 3,

,

,

,

Переброска коэффициентов:

у₁ = 1, то t₁ = ,

у₂ = 4, то t ₂ = 2,

, ,

, х - 2 = 1,

х - 2 = -1, х₂ = 3. Ответ: 1; 3.

х₁ = 1.

Вывод: Какой способ решения такого типа уравнений необходимо применить? Почему?

5. Подведение итогов урока.

6. Домашнее задание. § 6.3 (выучить теорию). № 6.17(кроме д), 6.19(б), 6.21(б,г,е), 6.23(а,в), 6.24(а).