- Учителю
- Методические рекомендации по проектированию логико-смысловых моделей и использованию их при обучении математике
Методические рекомендации по проектированию логико-смысловых моделей и использованию их при обучении математике
Краевое государственное бюджетное образовательное учреждение
среднего профессионального образования
«Агропромышленный техникум рп. Хор»
Методические рекомендации по проектированию логико-смысловых моделей и использованию их при обучении математике
Тешабаева Галина Владимировна

Преподаватель математики

Краевое государственное бюджетное образовательное учреждение
среднего профессионального образования «Агропромышленный
техникум рп. Хор»

682920, Россия, Хабаровский край, район им. Лазо, пос. Хор, ул. Менделеева, 13

тел./факс:8(42154)35466, E-mail: sk17-08@mail.ru

Определение ЛСМ
Логико-смысловое моделирование - метод представления понятия в виде логико-смысловой модели.
Логико-смысловая модель (ЛСМ) - это конкретное представление знаний на естественном языке в виде образа - модели.
Применение ЛСМ обеспечивает более быстрое и качественное осмысление темы, представленной моделью, за счет взаимодействия внутреннего плана мышления с вынесенной во внешний план ЛСМ в режиме аутодиалога.
На рисунке представлена ЛСМ обоснования особенностей восприятия.

ЛСМ обоснования особенностей восприятия информации.
Ценность технологии в том, что она не только повышает эффективность освоения учебного материала, но и является инструментом успешного формирования ключевых учебных компетентностей. В основе технологии лежит моделирование содержания - один из приемов проектной деятельности. Оно заключает в себе две тенденции: сначала разложение содержания на элементы (анализ), потом - объединение этих элементов (синтез). Создание модели привлекательно тем, что позволяет «свернуть», скомпоновать объемную информацию.
ЛСМ - технология, объединяющая вербальную и визуальную подачу материала. В ЛСМ производится структурирование содержания, связывание элементов структуры. Модель позволяет одновременно увидеть всю тему одного занятия или даже цикла занятий и каждый ее элемент в отдельности.
ЛСМ состоит из двух компонентов: смыслового (ключевые слова) и логического (порядок расположения смысловых единиц - это график - система координат, связывающий эти слова-понятия по смыслу).
Логико-смысловые модели обладают универсальностью, т.е. могут быть востребованы в преподавании любых учебных дисциплин, в любых учебных заведениях, в работе с учащимися различных возрастных групп.
Примеры таких моделей.

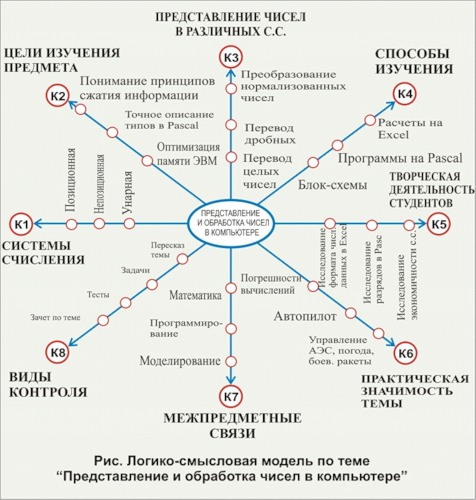
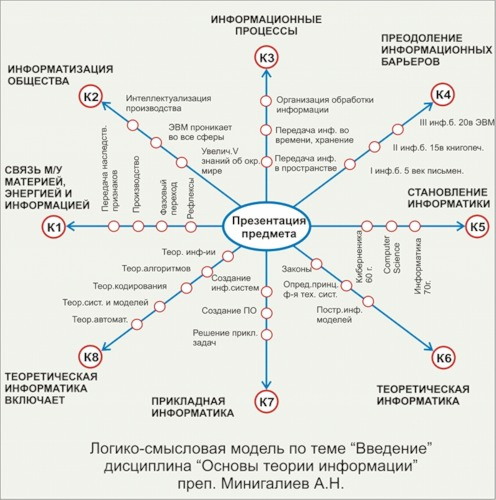
Модели выполняют функции:
1. Информационную - источник информации;
2.Коммуникативную - средство передачи информации;
3.Суммирующую - упорядочение и компоновка информации; 4.Контролирующую и стимулирующую - способ осознания, рефлексии.
Основой конструкции логико-смысловой модели является опорно-узловая система координат солярного (радиально-кругового) типа с помещёнными на ней ключевыми элементами содержания учебного материала на естественном языке. По образцу такой системы координат можно представить любую тему по любому учебному предмету; помимо этого, по такому же образцу можно разложить содержание каждой координаты и каждого узла любой координаты (свойство фрактальности, т.е. самоподобия, модели). Модель - в самом широком смысле слова - любой мысленный или знаковый образ представляемого объекта; как правило, она играет роль минисправочника.
К моделям, выполняющим инструментальные функции в обучении, предъявляются требования, которые рекомендуется учитывать их составителям:
- чёткая структура и логически удобная форма представляемого знания;
- "каркасный" характер (фиксация наиболее важных, узловых моментов);
- универсальность (пригодность для решения широкого спектра задач);
- психологическая поддержка пользователя (обеспечение режима самоорганизации).
При этом должны быть обеспечены полнота, логичность, компактность, удобство представления знаний, освещение гуманитарного фона.
Проектировщику ЛСМ необходимо действовать по следующему плану:
1 выбрать "каркас" (как правило, восьмилучевого вида);
2 определить круг изучаемых вопросов (тему, раздел знаний);
3 разбить тему на подтемы, т.е. сформировать смысловые группы;
4 сформулировать названия смысловых групп, расставить смысловые группы (координаты);
5 провести смысловую грануляцию знаний в каждой группе;
6 сформулировать названия опорных узлов и расставить их на координатных лучах;
7 выявить смысловые связи между объектами знаний.
При проектировании каждой темы в её состав включают следующие аспекты:
- этимологический (происхождение понятия);
- генетический (зарождение знания, его развитие, современное состояние);
- внутрипредметные и межпредметные связи знаний;
- прикладное значение знаний для человека, общества, природы;
отражение знаний в культуре, искусстве и т.д.
Преимущества ЛСМ:
-
Системное видение темы или раздела;
-
Содержательность;
-
Наглядность;
-
Дает возможность:
-
осуществить связь между предшествующими и последующими темами курса;
-
компактно и системно обучать структурированию знаний и логике;
-
организовать самостоятельную работу учащегося над конкретной темой при выполнении им творческого, исследовательского задания.
Возможности технологии дидактических многомерных инструментов:
- получить целостное представление об изучаемом объекте;
- осуществить связь между предшествующими и последующими темами курса;
- делить общие понятия на частные, выясняя при этом связи между ними и закономерности;
- компактно и системно обучать структурированию знаний и логике;
- организовать самостоятельную работу учащегося над конкретной темой при выполнении им творческого, исследовательского задания;
- избавлять учащихся от механического запоминания, снимать стресс перед восприятием большого объёма учебного материала;
- сформировать новый взгляд на учебный предмет, на предметный курс, на жизнь в целом;
- технологизировать деятельность учителя и учащегося для значительного облегчения их совместной работы.
На уроках я использую 7 логико-смысловых моделей:
«Арифметические действия»
«Портрет стереометрии»
«Симметрия»
«Тригонометрия»
« Формулы тригонометрии»
«Синус угла»
«Свойства sin![]() , cos
, cos![]() , tg
, tg![]() , ctg
, ctg![]() »
»
Предлагаю свой опыт работы с некоторыми из них
1.Модель «Арифметические действия» играет роль минисправочника. Учащиеся при составлении модели верно обозначили четыре арифметических действия (сложение, вычитание, умножение и деление), а вот возведение в степень и извлечение корня как арифметические действия не обозначали. При вычислительной работе учащиеся постоянно пользуются ЛСМ «Арифметические действия». (Приложение 1)
2. Модель «Портрет стереометрии». На уроке введения в стереометрию проводится вводное обобщение - целостное видение темы. Используя предметную наглядность (модели многогранников и тел вращения), с опорой на знания учащихся я знакомлю их с различными случаями расположения прямых и плоскостей в пространстве. Затем рассказываю об аксиоматическом построении геометрии, привожу факты из истории науки. В заключение урока, предлагаю учащимся привести примеры применения геометрических форм в окружающей жизни. После такой работы учащиеся наглядно представляют себе объём предстоящих знаний, последовательность изучения отдельных тем курса, связи между различными объектами знаний. Работа с моделью проводится систематически на протяжении всего времени изучения стереометрии. Использование модели позволяет сократить учебное время для изучения теории, а значит, уделить больше внимания решению задач. Появляется возможность знакомить учащихся с историей геометрической науки, с её ролью и местом среди других наук. Данная модель незаменима при обобщении знаний. (Приложение 2)
3. Логико-смысловая модель «Симметрия» - это результат коллективного труда учащихся 11-го класса. Объединённые в группы, они самостоятельно определили содержание симметрии. Модель является отражением межпредметной интеграции знаний по конкретной теме, она имеет ярко выраженную прикладную направленность. Эта модель может быть опорой знаний по данной теме при подготовке выступления на конкурсе исследовательских работ. Она может использоваться учителем и учащимися при знакомстве с содержанием различных разделов математики на разных этапах её изучения.
4. Тригонометрия - один из самых трудных для усвоения учащимися разделов школьной математики. По этой теме предлагаю 4 логико-смысловых модели.
Работа с моделью «Тригонометрия» проводится аналогично работе с моделью «Портрет стереометрии», т.к. эта модель- это обобщённое представление знаний раздела. «Практические приложения» (К 7) модели рассматриваются на уроке-семинаре, где учащиеся выступают со своими сообщениями-презентациями. Содержание координаты «Виды заданий» (К 4) определяется с привлечением знаний учащихся.
Модель «Формулы тригонометрии» - это развёрнутая координата «Формулы»(К 2) модели «Тригонометрия». Для осознанного и прочного усвоения тригонометрических формул (всего их более 40) выясняются логические связи между содержанием различных координат; учащиеся устанавливают, с помощью каких преобразований из одной группы формул получаются другие. Они учатся находить рациональные способы выполнения задания, решая его различными способами, т.е. применяя формулы различных групп.
Модель «Свойства sin![]() , cos
, cos![]() , tg
, tg![]() , ctg
, ctg![]() » расширенным содержанием координаты «Определение и свойства синуса и др.» (К 1) модели «Тригонометрия». На ней представлены все свойства синуса, косинуса, тангенса и котангенса угла, знание которых необходимо при выполнении различных заданий с тригонометрическими выражениями (упрощение, нахождение значений, сравнение и др.). Эта модель составлена на уроке вместе с учащимися после выполнения ими домашнего задания в группах.
» расширенным содержанием координаты «Определение и свойства синуса и др.» (К 1) модели «Тригонометрия». На ней представлены все свойства синуса, косинуса, тангенса и котангенса угла, знание которых необходимо при выполнении различных заданий с тригонометрическими выражениями (упрощение, нахождение значений, сравнение и др.). Эта модель составлена на уроке вместе с учащимися после выполнения ими домашнего задания в группах.
Примером использования свойства фрактальности ЛСМ является модель «Синус угла» .Своеобразный «портрет» синуса угла получается с помощью расширения содержания первого узла «sin ![]() » на первой координате «Определение и свойства синуса и др.» (К 1) модели «Тригонометрия». По аналогии с содержанием модели «Синус угла» учащиеся самостоятельно определяют содержание моделей для каждой из остальных тригонометрических функций. Результатом усвоения учащимися содержания данного раздела является свободное владение ими изученным материалом, что проявилось в умении выполнять задания, виды которых представлены на координатах 4, 5 и 6 модели «Тригонометрия».
» на первой координате «Определение и свойства синуса и др.» (К 1) модели «Тригонометрия». По аналогии с содержанием модели «Синус угла» учащиеся самостоятельно определяют содержание моделей для каждой из остальных тригонометрических функций. Результатом усвоения учащимися содержания данного раздела является свободное владение ими изученным материалом, что проявилось в умении выполнять задания, виды которых представлены на координатах 4, 5 и 6 модели «Тригонометрия».
Вывод: Научно обоснованная педагогическая технология только тогда даёт необходимые результаты, когда она одухотворена её соавтором и исполнителем - Учителем. Хочется надеяться, что предложенный опыт даст возможность коллегам попробовать свои силы в освоении данной технологии.
Литература:
-
Г.Валькова, A. Зайнуллина, В. Штейнберг «Дидактическая многомерная технология - логико-смысловое моделирование».
-
Е. Н. Куликова «Моделирование логико-смысловое»
-
Т. И. Фисенко «Способы формирования понятийного аппарата школьников в процессе изучения предметных тем» пособие для учителя Хабаровск 2012г.
-
Я. И. Груденов «Совершенствование методики работы учителя математики» М. «Просвещение» 1999г.
-
Селевко, Г. К. Педагогические технологии на основе дидактических и методических усовершенствований УВП. - М.: НИИ школьных технологий, 2005.-288 с.
-
Кулак Д. В. Неудахина Н. А. «Применение логико-смысловых моделей в обучении»
Приложение 1
 приложение 2
приложение 2
 приложение 3
приложение 3
