- Учителю
- Проект Сдать экзамен на отлично!
Проект Сдать экзамен на отлично!
Муниципальное бюджетное образовательное учреждение
средней общеобразовательной
школы №27
Сдать экзамен
на отлично!
Исполнитель:
Багаутдинова Татьяна Ринатовна
ученица 10-В класса
Руководитель:
Фахрутдинова Ольга Валентиновна
учитель математики
г. Серов
2012
Содержание:
1. Основная часть
3
1.1 История появления тестов
5
1.2.Что такое тест?
7
1.3 Преимущества и недостатки тестов
8
1.4 Виды тестов
10
1.5 Уровни тестов
12
1.6 Формы тестов
13
1.7 Как определить коэффициент усвоения знаний
16
2. Структура теста ГИА по математике
17
3 Исследование
3.1 Исследование тренировочных работ по теме: «Арифметическая прогрессия» 9 класс
3.2 Мониторинг результатов тренировочных работ
3.3 Мониторинг личных достижений
4. Заключение
18
19
5. Список литературы
6. Приложение
20
Введение
С ранних лет я мечтала стать учителем математики, я всегда интересовалась этим предметом. Мне нравилось считать, вычислять, решать различные задания. Математика - самая древняя наука. Она способствует логическому мышлению, тренировке памяти и саморазвитию. Эта наука одна из важных и значимых в жизни человека, поэтому она является обязательным предметом для сдачи экзаменов.
Мой учитель математики Ольга Валентиновна поделилась со мной мыслями о том, что когда она не использовала в системе тестовые технологии, показатель ЕГЭ в 2008 г. 11-в класса был 48% качества, а когда она начала использовать тесты на уроках, показатель повысился. Меня это сразу заинтересовала и поэтому я решила сама провести исследование на примере государственной итоговой аттестации в новой форме.
Проблема: как удачно сдать государственную итоговую аттестацию в новой форме по математики.
Гипотеза: предположим, что знания о тестовых технологиях повлияют на результат государственной итоговой аттестации в новой форме по математики.
Цель: изучение тестовых технологий, как одного из факторов качественной подготовки к государственной итоговой аттестации в новой форме по математики.
Задачи: 1. познакомиться с тестовыми технологиями;
2. рассмотреть структуру, виды, формы, уровни тестов;
3. составить математическую копилку по теме «Арифметическая и геометрическая прогрессии» 9 класс;
4. апробировать тематические тесты на учащихся 9-х классов;
5. проанализировать личный мониторинг подготовки к государственной итоговой аттестации в новой форме.
История появления тестов
Тесты возникли после периода, когда в Европе уже сложились первые педагогические системы Коменского, Ушинского, Дистервега, Герберта, Песталоцци и др. Идея Гельвеция о всемогуществе воспитания была подхвачена Марксом и абсолютизирована на российской почве с начала 30-х годов - в форме господствующей идеи советской педагогической науки, основным предметом и целью которой стало воспитание в духе преданности известным лицам и идеям; остальные составляющие, такие как образование и обучение, могли быть только воспитывающими в том же духе. Побочным продуктом этой идеи стала так называемая "воспитательная концепция" профориентации, цель и методы которой выродились в пропаганду рабочих профессий и в противоречащее здравому смыслу отрицание тестов.
Тесты запретили в 1936 году как "буржуазные и вредные", но истинные причины запрета - расстановка сил в политической борьбе того периода. Воцарившаяся после запрета ситуация отрицательного отношения к тестам не давала практической возможности публиковать что-либо в их защиту. И эта ситуация продолжалась в течение примерно сорока лет. В течение всего этого времени печатались, в основном, статьи о вредности тестов, о недопустимости использования последних в отечественной педагогической науке и практике. Соответственно, в этих условиях трудно было найти желающих заниматься тестовой проблематикой и вводить ее в планы научно-исследовательских учреждений, а также писать труды на "недиссертабельную" тему. Педагогика того времени потеряла интерес к тестам и к проведению эмпирических исследований; отчасти поэтому она в течение многих лет оставалась одной из немногих общественных наук, лишенных качественного эмпирического базиса. С той далекой поры эмпирическое направление педагогических исследований так и осталось в неразвитом состоянии. Хотя в тридцатых годах практическая работа по тестам затормозилась, научное изучение действительных возможностей этого метода в СССР полностью не прекращалось. Часть тестов применялась под видом контрольных заданий, испытаний. И наоборот, различные испытания нередко назывались тестами. Практика тестирования характеризовалась серьезными противоречиями, что привело к запрету применения тестов в сфере образования, профотбора и профориентации.
С тех пор отношение к тестам стало неоднозначным. Одни видели в тестовом контроле средство принижения роли педагога, воспринимали тесты как средство выражения недоверия к традиционно выставляемым оценкам и потому проявляли определенную настороженность. Другие считали сами тесты виновными в различных нарушениях и потому отвергали идею тестового контроля знаний, как говорится, с порога. И только немногие рассматривали их как средство радикального преобразования учебного процесса в сторону его объективизации - и становились энтузиастами этого метода. Как прозорливо отмечал П.П. Болонский, тесты - это больше, чем средство контроля; это средство рационализации школьного дела.
Поскольку тесты считались основным методом педологии, то отказав
в научности педологии, руководители педагогической науки тех лет
отказались признать также и научность тестов. Здесь было намеренно
допущено сразу несколько ошибок, возможно, преднамеренных. Одна - в
отношении к педологии, которая имела ряд интересных научных
достижений, не вписывавшихся в современную ей педагогику. Вторая
ошибка - в признании тестов в качестве специфического метода
педологии. Хотя известно, что абсолютно специфических частных
методов (в которых бы не присутствовали элементы познания,
применяемые в других методах) нет. И третья ошибка - отказ в
признании научности тестового метода. Это сильно затормозило
развитие самой педагогической науки, лишив ее предпосылок для
разработки самого эффективного метода контроля знаний.
Начиная с 30-х годов, в контроле знаний наметились две основные
тенденции. Первая связана с применением традиционных форм и
длительным, растянувшимся на полвека, периодом активного
игнорирования тестов. Эта тенденция привела в наши дни к тотальному
субъективизму в выставлении оценок, несопоставимости оценок, к
образовательно-технологическому и организационно-педагогическому
отставанию школы от общемирового образовательного процесса, к
несопоставимым с имеющимся качеством выпускников большим затратам
живого труда преподавателей. Не секрет, что исторически
субъективность всегда играла большую роль, чем объективность. В
сфере образования это проявлялось в повсеместной приверженности к
традиционным экзаменам, в то время как во многих странах уже давно
тот кто учит не берется ставить итоговые оценки учащимся за свою
же, по существу, работу. Там это считается нарушением
профессиональной этики и потому общественное мнение склоняется в
пользу независимого тестового контроля знаний.
Что такое тест?
Для того, чтобы узнать, что такое тест, я собрала много материала и для начала нашла определение самого слова.
Тест (англ. test) - испытание, проверка, анализ.
Следующей задачей для меня являлось найти определение, содержащее главный смысл.
Тест - стандартизированные задания, по результатам, выполнения которых судят о знаниях, умениях, навыках испытуемого.
Также в информации о тестовых технологиях я нашла особенности применения.
Особенности применение: быстрота исполнения, удобство проверки, вариативность содержания, технологичность приготовления, простота и скорость получения результата.
В ходе своей работы, у меня неоднократно возникал вопрос: «Как влияют тестовые технологии на качество образования?»
Влияние тестовых технологий на качество образования: возможность получения объективного (полученного без участия людей) результата обучения, оперативность обратной связи, разнообразие способов проверки результатов обучения, удобство получения статистики результатов обучения, необходимой для анализа образовательной ситуации.
И, конечно же, заинтересовали меня ещё и функции тестов.
Диагностическая функция заключается в выявлении уровня знаний, умений, навыков учащегося. Это основная, и самая очевидная функция тестирования. По объективности, широте и скорости диагностирования, тестирование превосходит все остальные формы педагогического контроля.
Обучающая функция тестирования состоит в мотивировании учащегося к активизации работы по усвоению учебного материала.
Воспитательная функция проявляется в периодичности и неизбежности тестового контроля. Это дисциплинирует, организует и направляет деятельность учащихся, помогает выявить и устранить пробелы в знаниях, формирует стремление развить свои способности.
Преимущества и недостатки тестирования
Чтобы начать исследование, нужно обязательно знать преимущества и недостатки тестов, так как это поможет мне решить главные задачи.
Преимущества тестирования:
1. Тестирование является более качественным и объективным способом оценивания, его объективность достигается путем стандартизации процедуры проведения, проверки показателей качества заданий и тестов целиком.
2. Тестирование - более справедливый метод, оно ставит всех учащихся в равные условия, как в процессе контроля, так и в процессе оценки, практически исключая субъективизм преподавателя.
3. Тесты это более объемный инструмент, поскольку тестирование может включать в себя задания по всем темам курса, в то время как на устный экзамен обычно выносится 2-4 темы, а на письменный - 3 - 5. Это позволяет выявить знания учащегося по всему курсу, исключив элемент случайности при вытаскивании билета. При помощи тестирования можно установить уровень знаний учащегося по предмету в целом и по отдельным его разделам.
4. Тест это более точный инструмент, так, например, шкала оценивания теста из 20 вопросов, состоит из 20 делений, в то время, как обычная шкала оценки знаний - только из четырех.
Недостатки тестирования:
1. Данные, получаемые преподавателем в результате тестирования, хотя и включают в себя информацию о пробелах в знаниях по конкретным разделам, но не позволяют судить о причинах этих пробелов.
2. Тест не позволяет проверять и оценивать высокие, продуктивные уровни знаний, связанные с творчеством, то есть вероятностные, абстрактные и методологические знания.
3. В тестировании присутствует элемент случайности. Например, учащийся, не ответивший на простой вопрос, может дать правильный ответ на более сложный. Причиной этого может быть, как случайная ошибка в первом вопросе, так и угадывание ответа во втором. Это искажает результаты теста и приводит к необходимости учета вероятностной составляющей при их анализе.
Продолжая узнавать и выделять для себя что-то новое, я выделила 5 видов тестов, которые изображены на схеме:
В


 иды
тестов:
иды
тестов:
![]()
По способу предъявления
По цели назначения
По деятельности
По месту использования
По объему содержания и времени проведения
Каждый вид тестов подразумевает под собой ещё несколько подвидов (приложения №1, №2, №3):
В

 иды
тестов по способу предъявления
иды
тестов по способу предъявления
С выбором готового ответа
С предъявлением ответа в краткой форме
С предъявлением развернутого ответа



 Виды тестов по цели назначения
Виды тестов по цели назначения
Первичное закрепление
Контроль ЗУН
Разминка в начале урока
тренажер
Р
Сопоставление явлений и его характеристики






 азличные виды тестов по
деятельности
азличные виды тестов по
деятельности
Индивидуальный опрос по карточкам
Распознавание понятий
Составление последовательности
Тренировочная работа
Конструирование моделей
Заполнение пропусков
Фронтальный устный опрос
Контрольная работа
Самостоятельная работа
Диктант
Зачетная работа
В


 иды
тестов по месту использования
иды
тестов по месту использования
Актуализация ЗУН
Первичное закрепление ЗУН
Контроль ЗУН
Упражнения
В

 иды
тестов по объему содержания и времени проведения:
иды
тестов по объему содержания и времени проведения:
Стартовый контроль
Тематические тесты
Итоговый зачет
Промежуточная аттестация
Итоговая аттестация
Следующее, что я узнала - это уровни, которые распределяют тесты по степени сложности. Все 4 вида указаны в схеме:
У

 ровни тестов
ровни тестов
Тесты нулевого уровня
Тесты 1 уровня
Тесты 2 уровня
Тесты 3 уровня
Чтобы более подробно познакомиться со схемой, я охарактеризовала каждый уровень.
1.Тесты нулевого уровня
•Умения выполнять действие при внешне заданных правилах
( с «подсказкой»)
•Умение отличать правильное использование знания от неправильного.
Тесты этого уровня должны требовать от ученика выполнение деятельности по узнаванию
2.Тест 1 уровня
•Умения воспроизводить математические содержание по памяти
•Умение решать типовые задачи самостоятельно, воспроизведя по памяти способ решения.
3.Тесты 2 уровня
•Умения воспроизводить и преобразовывать усвоенную информацию.
•Умения применять усвоенные решения типовых задач в нетипичной ситуации, но отчасти знакомой ученику.
4.Тесты 3 уровня
•Творческий уровень усвоения материала, сопровождающиеся возможностью ученика переносить усвоенные методы (приемы) решения задач в совершенно новую для него ситуацию, находить новые способы решения задачи. Задачи математических олимпиад часто соответствуют этому уровню сложности.
Тесты делятся не только по видам и уровням, а также по формам. Эти формы указаны в схеме (приложения №4, №5, №6):
Ф


 ормы тестов
ормы тестов
Задания открытого типа
Задания закрытого типа
Задания с множественным выбором
Задание на соответствие
Рассматривая формы, я узнала о том, как каждый тест, относящийся к той или иной форме, составляется и как формируется само задание.
1.Задания открытого типа:
а) вместо многоточия вписать только одно слово или знак, символ и т. д.
б) вместо многоточия вписать словосочетание фразу, предложение.
Формулировка задания: закончите предложение, дополните определение, впишите вместо многоточия правильный ответ и т. д.
Правила составления таких заданий:
-использовать не более трех пропусков подряд, лучше 1-2;
-дополнять нужно наиболее важное - то, что проверяем;
-дополнение лучше ставить в конце предложения;
-вопрос формулируем четко;
-ответ должен быть четким и однозначным.
Эти задания нравятся детям, снижают утомляемость.
Наибольшая трудность при составлении - наличие однозначного ответа.
2.Задания закрытого типа - альтернативный ответ.
Дается два варианта ответов: да/нет или правильно/ неправильно.
Формулировка задания: Верно ли высказывание; отметьте только верные высказывания и т. п.
Правила составления таких заданий:
-вопрос должен содержать одну законченную мысль;
-в вопросе надо избегать слов, дающих возможность учащимся догадаться о правильном ответе («иногда», «обычно» и т. п.)
-вопрос должен быть четко сформулирован, избегать слов «мало», «много», «меньше», «больше» и т. п.;
-не должно быть пространственных выражений и вопросов типа «Не считаете ли вы, что...»;
-число ответов «да» и «нет» в тесте должно быть приблизительно равным, чтобы исключить тенденцию отвечать одинаково.
Использование таких заданий в виде отдельного вопроса часто приводит к простому тестированию.
Подходят такие задания для проверки усвоения сложных определений, сложных процессов, графиков, диаграмм, таблиц, схем, которые могут быть разбиты на части.
3.Задания с множественным выбором - основной вид заданий, применяемый в тестах.
Формулируется задание и предлагаются варианты ответов. Задачи формулируются так, чтобы было не менее 3 правдоподобных ответов, похожих на правильные.
Правила составления таких заданий:
-вопрос должен содержать только одну мысль или утверждение;
-все ответы должны быть грамматически согласованы с основной частью задания;
-как можно реже использовать отрицание в основной части;
-ответ не должен зависеть от предыдущих ответов;
-лучше использовать длинный вопрос и короткий ответ;
-место правильного ответа не должно повторяться из вопроса к вопросу;
-если ставится количественный вопрос, то ответы располагаются от меньшего к большему;
-правильные и неправильные ответы должны быть однозначны по содержанию, структуре и количеству слов.
4.Задания на соответствие
Это задания где необходимо найти или приравнять части, элементы, понятия, восстановить соответствие между элементами двух списков.
Формулировка задания: установите стрелочками соответствие и т. п.
Подходят эти задания для выяснения фактической информации. Главный «минус» этих заданий - тривиальность (простота) тестирования.
Для усложнения заданий и исключения угадывания длина списков не должна совпадать.
Изучив виды, уровни, формы тестов, я создала математическую копилку по теме: «Арифметическая и геометрическая прогрессии» 9 класс.
(приложения №1-8)
Как определить коэффициент усвоения знаний
По мнению Беспалько В.П. и Татур Ю.Г., тестирование должно быть
измерением качества усвоения знаний, умений и навыков. Для того
чтобы определить коэффициент усвоения знаний (Кus), нужно число
правильных ответов - А разделить на число заданий в предлагаемых
тестах - Р: ![]() .
.
Если Кus > 0,7, то процесс обучения можно считать завершенным. При усвоении знаний с Кus ≤ 0,7 студент систематически совершает ошибки и неспособен к их исправлению из-за неумения их находить.
Таким образом, существует формула для определения коэффициента усвоения знаний.
Структура теста ГИА по математике
Тест ГИА по математике разделен на две части, отличающиеся по сложности и форме приведения ответа:
- часть 1 - задания базового типа сложности с выбором одного
правильного ответа из предложенных, на решение 18 задач отводится
90 минут (1,5 часа);
- часть 2 - задачи повышенного уровня сложности, требуют подробного
решения и ответа, на 5 задач дается 150 минут (2,5 часа).
Государственная итоговая аттестация (ГИА) по математике (алгебре) 2012 - обязательный экзамен в 9-м классе. Математику необходимо сдавать для перевода в 10-й класс и получения аттестата о неполном среднем образовании. Если же вы собираетесь продолжать обучение в физико-математическом классе, то потребуется сдать математику на высокий балл. ГИА был введен в 9-м классе специально для более точной оценки знаний школьников при зачислении их в профильные классы.
Например, когда у школьника оценка «4», то непонятно: или он знает чуть выше тройки, или немного не дотянул до пятерки. Все становится понятнее, когда больше градаций отметок, как в ГИА, - от 8 до 33, таким образом, четверке соответствуют оценки от 15 до 21.
3.Исследование:
3.1 Мною созданы тренировочные работы для учащихся 9-х классов: 1 вариант - с выбором ответа, 2 вариант - без выбора ответа. Анализ данной работы подтвердил мою гипотезу, что задания с выбором ответа выполнены более качественно, а значит приведет к хорошему результату государственной итоговой аттестации.
3.2 Я проанализировала результаты работ учащихся 9-го класса и
на основе их создала мониторинг.
Мониторинг тренировочных работ по теме:
«Арифметическая прогрессия» 9 класс
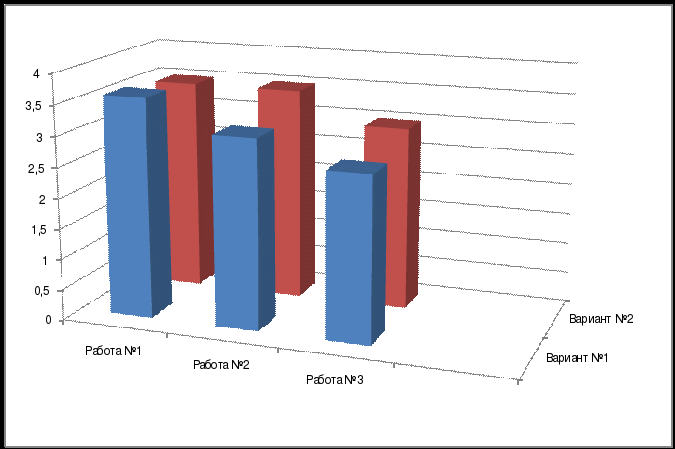
1 вариант - задания с выбором ответа
2 вариант - задания с кратким ответом
1 работа - тесты первого уровня
2 работа - тесты второго уровня
3 работа - тесты третьего уровня
Мониторинг тренировочных работ по теме:
«Арифметическая прогрессия» 9 класс
1 работа1 вариант
2 вариант
«5»
1
4
«4»
6
1
«3»
1
3
«2»
2
3
Средний балл
3,6
3,5
2 работа1 вариант
2 вариант
«5»
1
4
«4»
4
2
«3»
2
0
«2»
2
6
Средний балл
3,5
3,1
3 работа1 вариант
2 вариант
«5»
3
0
«4»
2
0
«3»
3
9
«2»
0
4
Средний балл
4
2,7
3.3 Изучение тестовых технологий и системный характер проведение тренировочных работ по подготовке государственной итоговой аттестации привел меня к отличному результату. На диаграмме показан мониторинг личных достижений 2010-2011 учебного года.
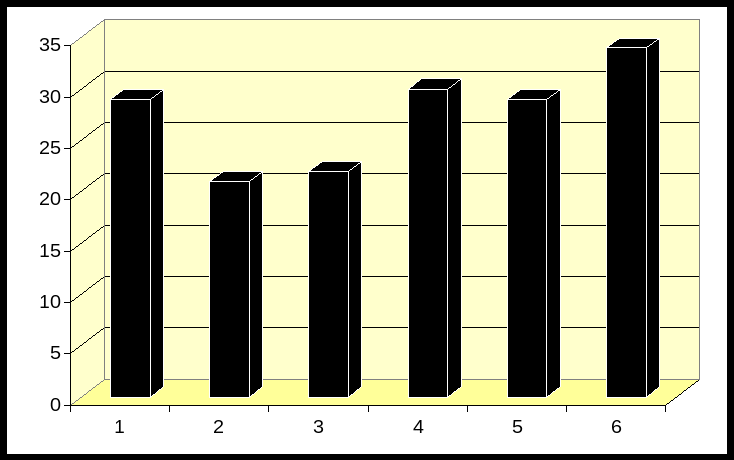
Заключение
Тестовые технологии - один из самых удобных и распространенных методов проверки знаний. Можно ли, заранее ознакомившись и изучив тестовые технологии, сдать итоговую аттестацию по математике в новой форме на хороший балл? Я думаю, что да! Подтверждение этому является мой личный опыт сдачи ГИА на 100% (34 балла).
Во-первых, дополнительная информация о тестах поможет быстрее разобраться при работе и привыкнуть к новой форме сдачи государственной итоговой аттестации.
Во-вторых, чтобы уметь решать тесты нужно долго тренироваться, а также знать различные способы и подходы к их решению.
В ходе моей работы создана математическая копилка по теме: «Арифметическая и геометрическая прогрессии» 9 класс. Я думаю она поможет качественно подготовиться выпускникам 9-х классов к государственной итоговой аттестации в новой форме. Тренировочные работы, проведенные в 9-ом классе, помогут учащимся закрепить знания по данной теме, а также получить опыт работы с тестами. Предложенные учащимся памятки помогут при работе с тестовыми заданиями. Мною создан буклет по теме: «Арифметическая и геометрическая прогрессии», который поможет выполнить задания данной темы в рамках ГИА по математики.
Поставленные перед собой задачи выполнены в полном объеме. Надеюсь, что мои труды помогут выпускникам сдать экзамен на отлично.
Список литературы:
-
Сайт www.testent.ru.
-
Сайт school707.ru
-
Сборник заданий для проведения письменного экзамена по алгебре основной школы. 9 класс / Л.В. Кузнецова, Е. А. Бунимович, Б.П. Пигарев, С. Б. Суворова. - 13-е изд., стереотип. - М. : Дрофа, 2007. - 191, [1] с. : ил.
-
Сайт www.google.ru
-
Алгебра. 9класс : учеб. Для общеобразоват. Учреждений / [Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др.]. - 16-е изд. - М.: Просвещение, 2011. - 287 с.: ил. - ISBN 978-5-09-020677-8.
Приложение
Как работать с тестами
Памятка
Тренируйтесь!
Чем больше вы решите типовых тестов, тем больше опыта получите.
Сейчас продается достаточное количество книг (сборников тестов) с
ответами на их задания и примерами решения. Также стоит отметить,
что задачи из этих сборников попадаются и на реальных тестах. Решив
достаточное количество тестов, вы усвоите их основные конструкции.
Большинство заданий похожи и отличаются только величинами данных
или названиями предметов.
Торопитесь!
Когда научитесь решать медленно, постепенно ускоряйте темп. После
чего делайте задания на скорость, пытаясь эмулировать условия,
приближенные к реальности.
Пропускайте!
Если после прочтения задания вы ничего не поняли, то смело его
пропускайте, даже если тест находиться в группе "легких заданий".
Ни в коем случае не тратьте на него время вначале.
Угадывайте!
Если у вас нет вообще никаких идей насчет правильного варианта
ответа, то на несколько секунд закройте глаза, стараясь ни о чем не
думать, а после ставьте первое, что придет в голову. Вообще
интуиция очень мощная вещь, которая тренируется, как и все
остальное.
Исключайте!
Решая определенный тест, вы заметите, что некоторые варианты
ответов никак не могут подойти под данное условие. Рассуждая и
постепенно отсекая неподходящие варианты, в конце концов можно
найти правильный.
Думайте только об одном задании.
Решая любую задачу, будь-то тест или что-нибудь из жизни, всегда
думайте в одно время о чем-то одном. Не распыляйтесь. Не
переживайте о неудачах в предыдущих заданиях, ведь время еще есть.
Читайте задание до конца.
Очень часто, прочитав первые два предложения и узнав в ней похожую,
ранее прочитанную задачу, бросаются ставить подходящий ответ. Это
приводит к самым досадным ошибкам. Всегда читайте задания до конца!
Не печальтесь.
Если вы решили не все тесты, то знайте следующее: в тестах
запланировано несколько заданий, с которыми вы просто физически не
должны справиться за отведенное время. Возможно, вы решите не все
задания, но очень много людей решит их еще меньше. Может получиться
так, что ваш невысокий бал относительно других будет просто
недосягаем.
Два этапа.
Решение тестов должно проходить в два этапа. Сначала проходите по
первому кругу, решая все то, что наверняка знаете. Потом
возвращаетесь к тому, что пропустили.
Памятка для учащихся: тактика работы с тестами по математике.
-
Решайте задачи в удобной для вас последовательности;
-
Работайте быстро без излишней торопливости: лучше сделать меньше, но правильно. Помните правило: « Поспешай не торопясь!» .
-
Внимательно прочитайте условие задачи, засекайте время и начинайте;
4.Не пытайтесь угадывать ответ, не теряйте время;
5.Если задача знакомая, решите ее и принимайтесь за
следующую;
«Знакомая» тестовая задача («Это я знаю!»)- это простая для Вас
задача.
Вы умеете ее решать, уверены в этом и можете быстро найти ответ.
6.Если задача техническая, поставьте «+» против номера
этой-задачи в черновике и приступайте к следующей;
«Техническая» тестовая задача (« Это я сделаю») -это известная Вам
задача. Вы умеете ее решать, но для этого Вам требуется время. Вы
не можете быстро найти ответ.
7. Если задача неизвестная, не раздумывая, беритесь за следующую задачу;
« Неизвестная» тестовая задача («Надо подумать») - это задача, на первый взгляд, незнакомая, над поиском ее решения Вам нужно подумать
-
Когда решены все «знакомые» задачи, начинайте решать все «технические»;
-
Когда решены все «технические задачи», думайте над решением «неизвестных» задач.
-
Если Ваш ответ не совпадает ни с одним из указанных, ищите ошибку в решении.
Приложение №1
Тесты с готовым ответом с выбором
-
Дана арифметическая прогрессия -3,5;-2;… Найдите номер члена этой прогрессии, равного 59,5.
А) 44 Б) 43 В)34 Г) Нет такого номера
2) Найдите сумму первых шестнадцати членов арифметической прогрессии, заданной формулой an=6n+2…
А) 864 Б) 848 В) 792 Г) 716
3) Сумма второго и третьего членов арифметической прогрессии равна 16, а разность прогрессии равна4. Найдите первый член прогрессии.
А) 2 Б) 4 В) 5 Г) 6
-
Сколько членов арифметической прогрессии -2,2… меньше числа 55?
А) 15 Б) 19 В) 16 Г) 13
-
Сумма четвертого и пятого членов арифметической прогрессии равна 14. Чему равна сумма первых восьми членов прогрессии?
А) 56 Б) 75 В) 52 Г) 112
-
Найдите первый член арифметической прогрессии а1;а2;4,8…
А) 1 Б) 12 В) -4 Г) -1
-
Дана арифметическая прогрессия 8,2;6,6;… Найдите номер члена этой прогрессии, равного -15,8
А) 16 Б) 14 В) 17 Г) Нет такого номера
-
Найдите сумму первых четырнадцати членов арифметической прогрессии, заданной формулой an=5n-1
А) 511 Б) 497 В) 1022 Г) 1400
-
Третий член арифметической прогрессии равен 6, а пятый равен 10. Найдите первый член прогрессии.
А) 1 Б) 2 В) -1 Г) 0
-
Сколько членов арифметической прогрессии -12,-8,… меньше числа 48?
А) 15 Б) 18 в) 16 Г) 12
-
Четвертый член арифметической прогрессии равен 18. Чему равна сумма первых семи членов прогрессии?
А) 80 Б) 126 В) 72 Г) 96
12) Укажите формулу, задающую число а, кратное пяти (n - натуральное число).
А) an=7n Б) an=5n В) an=n+5 Г)
![]()
-
Укажите формулу, задающую при всех натуральных n числа а, которые дают при делении на 5 остаток 1?
А)an=5(n+5) Б) an=n+6 В)
an=5n-4 Г) ![]()
14) Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условия a70>0.
А) an=3n-210 Б) an=3n-400 В) an=-3n+500 Г) an=-3n
-
Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условия а90>0.
А) an=-4n+500 Б) an=-4n В) an=4n-400 Г) an=4n-360
-
Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условия а25<0.
А) an=2n Б) an=-2n+50 В) an=-2n+100 Г) an=2n-100
-
Из арифметических прогрессий, заданных формулой n-го члена, выберите убывающую.
А) an=2n -3 Б) an=4-n В) an=9+5n Г) an=4+3n
-
Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условие а18-а3>45.
А) an=4-2n Б) an=46+n В) an=18+3n Г) an=1+4n
-
Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условие а15-а4<12.
А) an=1+2n Б) an=1+2n В) an=3n-1 Г) an=14n-1
-
Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, разность которой кратна 3.
А) an=2n+3 Б) an=4n-1 В) an=5n-9 Г) an=4-3n
21) Из числовой последовательности, заданной формулой n-го члена, выберите ту, для которой выполняется условие а4>115.
А) 2*3n-1 Б) 2*4n-1 В) 3n-1 Г) 4n-1
22)Сколько из следующих последовательностей
А) 3;6;9;12 Б) 2;4;8;16 В)7;4;1;-3 Г)8;8;8;8
Являются арифметическими?
23)Последовательность задана формулой аn=n2-2n+1. Вычислите 23-ий член этой последовательности.
А)483 Б) 484 В) 575 Г) 576
24)Известны шестой и седьмой члены арифметической прогрессии …16;13;… Укажите номер члена, начиная с которого члены этой прогрессии отрицательны.
А) 8 Б) 12 В) 10 Г) 9
25) В арифметической прогрессии а1=-2, d=3. Найдите а20.
А) 55 Б) 47 В) 57 Г) 45
Приложение №2
Тесты с кратким ответом
-
Дана арифметическая прогрессия (аn), где аn=2n+1. Найдите сумму ее членов с одиннадцатый по двадцатый включительно.
-
Составьте формулу n-го члена геометрической прогрессии 3;-6;…
-
Найдите седьмой член геометрической прогрессии (bn), если b5=
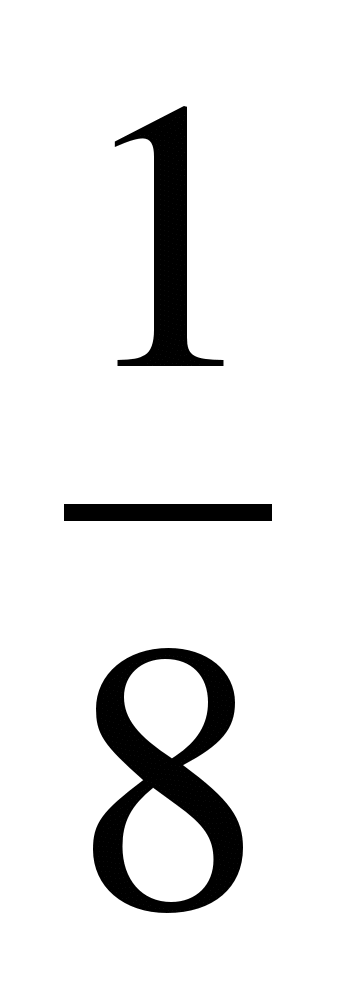 ; q=2
; q=2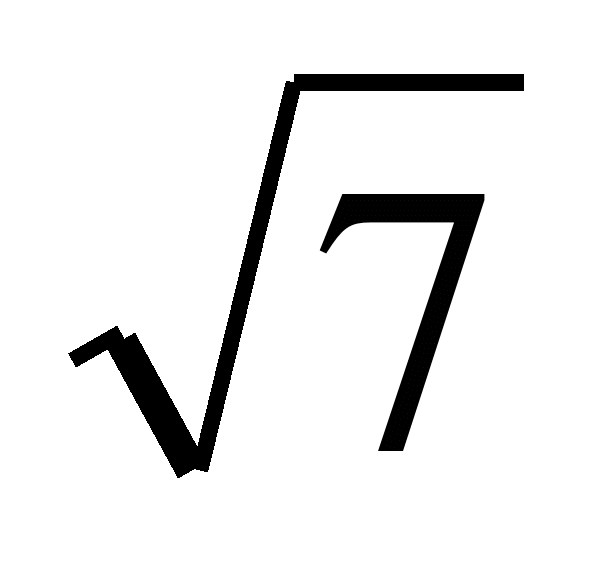 .
.
-
Выписано несколько последовательных членов арифметической прогрессии: …;-7;-1;а;… Найдите член прогрессии, обозначенный буквой а.
-
Выписано несколько последовательных членов арифметической прогрессии: …;17;а;29;… Найдите разность прогрессии.
-
Сумма пятого и четырнадцатого членов арифметической прогрессии равна 25. Найдите сумму первых восемнадцати членов этой прогрессии.
-
Геометрическая прогрессия (bn) задана условиями bn=3, bn+1= bn*2. Укажите формулу n-го члена.
-
Последовательность задана формулой аn=
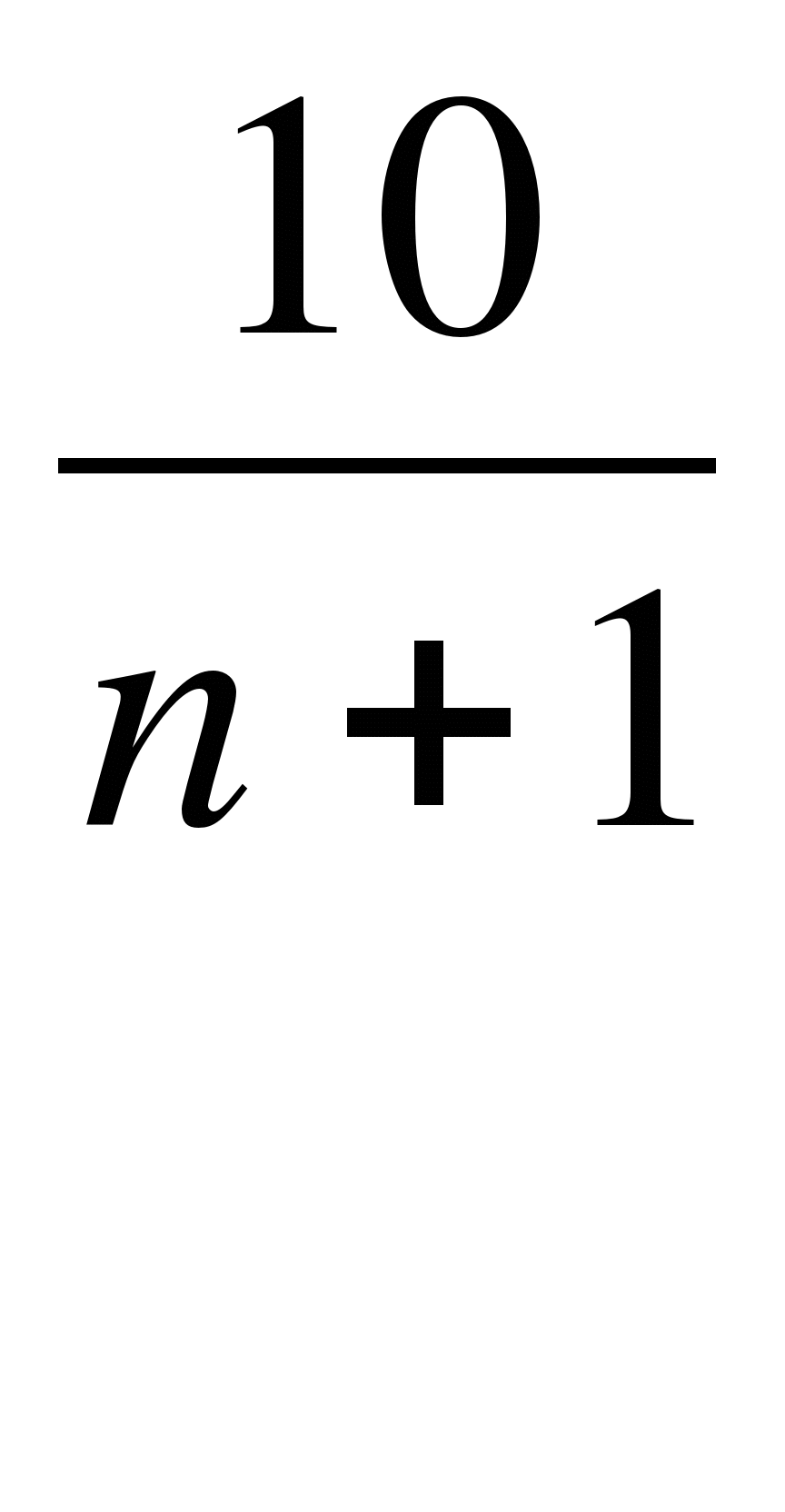 . Сколько
членов этой последовательности больше 1?
. Сколько
членов этой последовательности больше 1?
-
Напишите формулу для нахождения двадцатого члена арифметической прогрессии.
-
Найдите сумму двадцати членов арифметической прогрессии: -23;-20;…
-
В Арифметической прогрессии 1,2;1,7;2,2;… Найдите двадцатый ее член.
-
Какой номер имеет член арифметической прогрессии равный 21, если первый член прогрессии равен 4, а разность равна3.
-
Чему равен знаменатель прогрессии 33n+1?
-
Геометрическая прогрессия (bn) задана условиями b1=2, bn+1=bn*
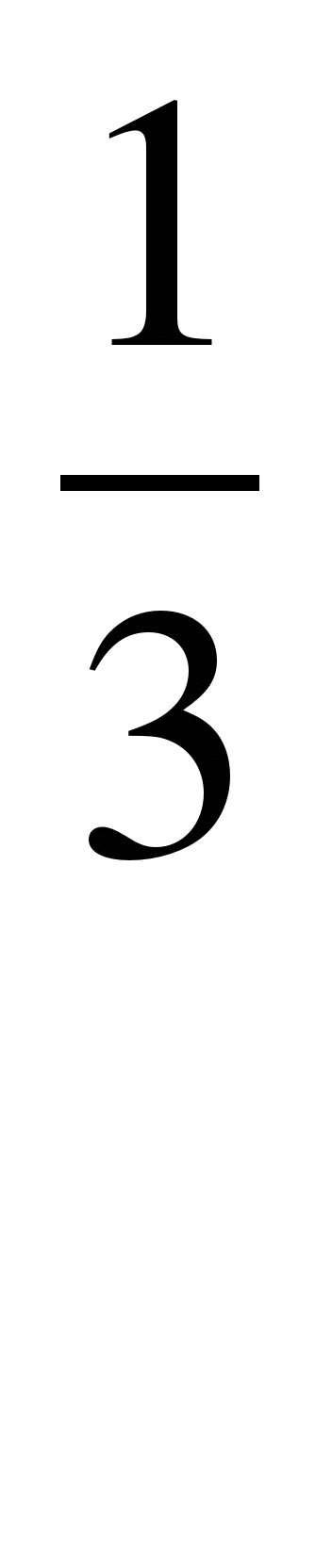 . Укажите формулу n-го члена
этой прогрессии.
. Укажите формулу n-го члена
этой прогрессии.
-
Запишите первые три члена последовательности, заданной формулой n-го члена: an=
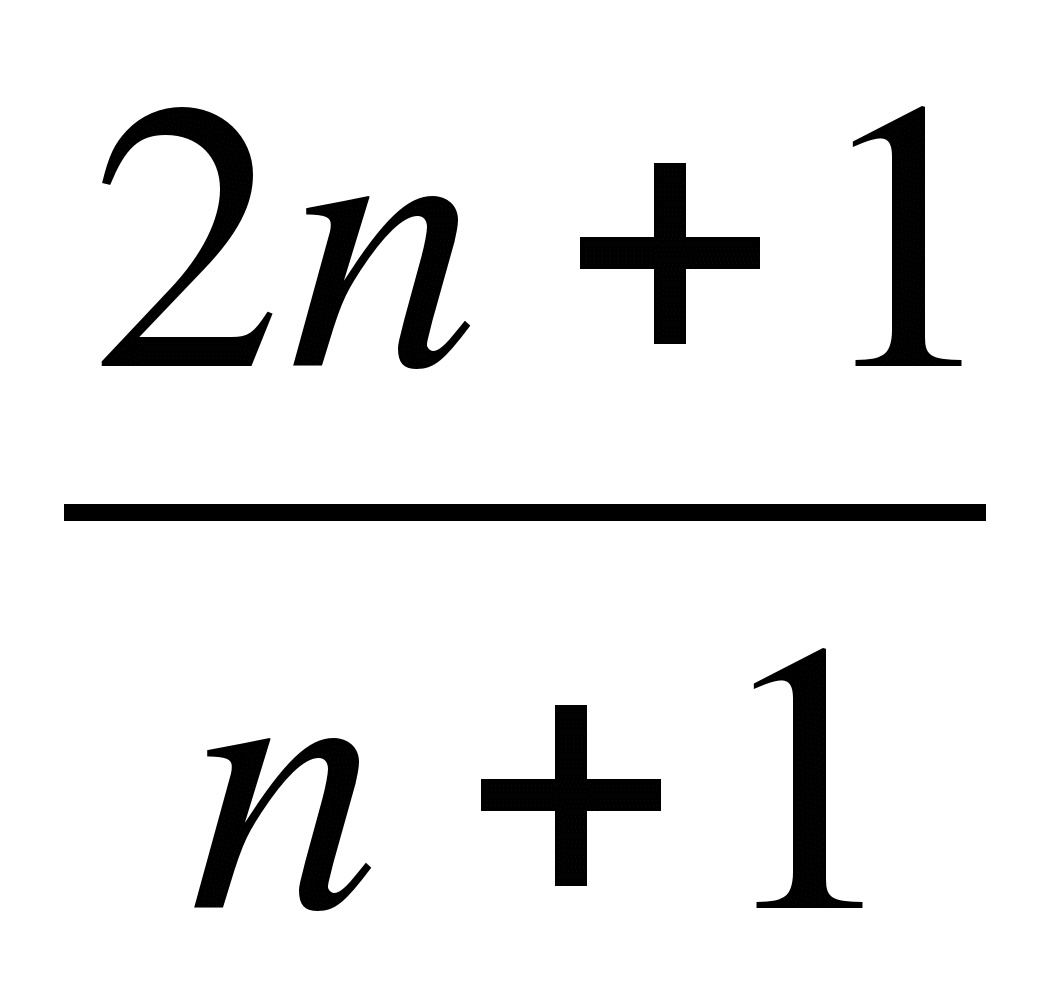 . Одному пропуску
соответствует только одно число.
. Одному пропуску
соответствует только одно число.
-
Числовая последовательность задана формулой n-го члена: an=
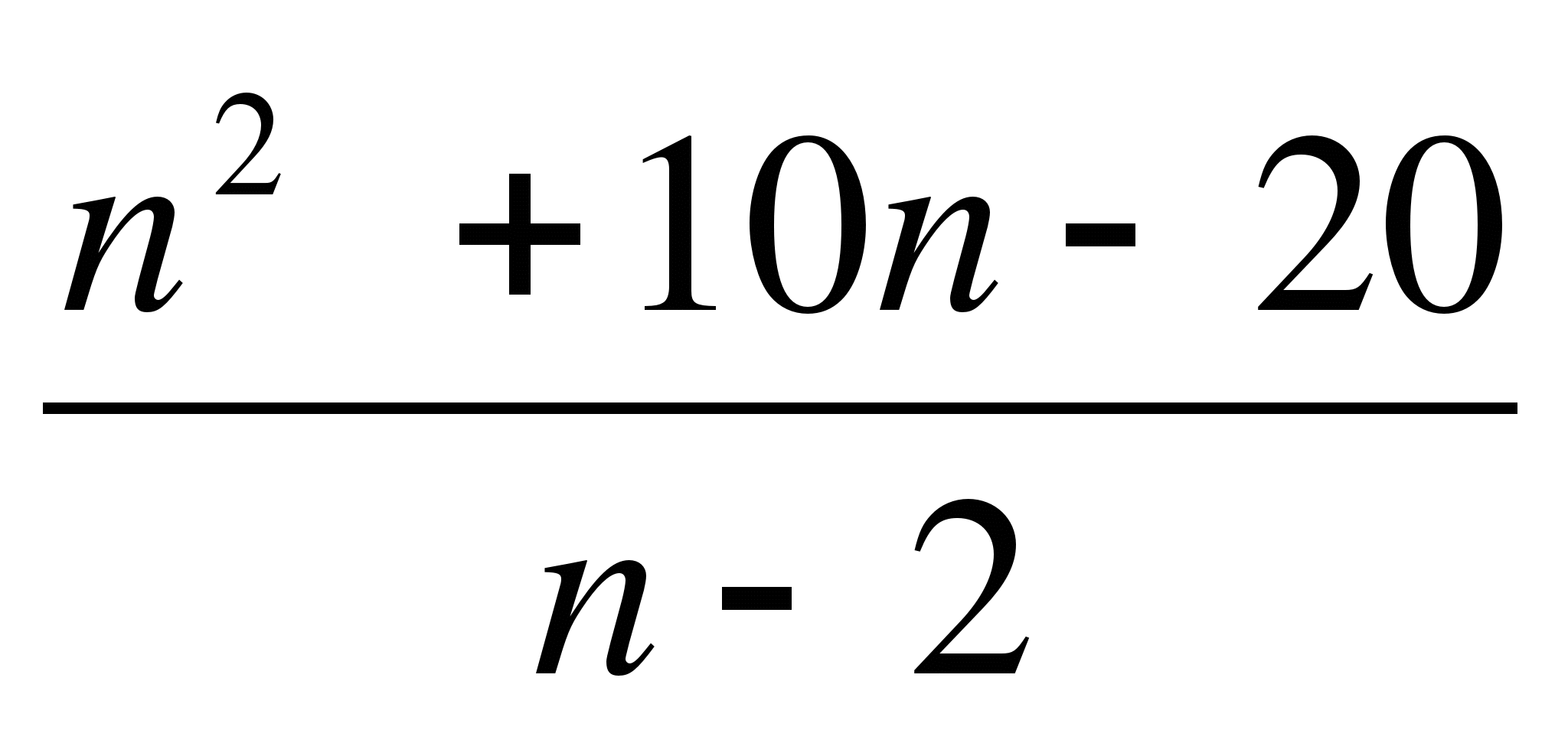 . Найдите номер
члена последовательности, равного 9.
. Найдите номер
члена последовательности, равного 9.
-
Составьте формулу для вычисления суммы всех натуральных чисел от 4 до n включительно.
-
В геометрической прогрессии (bn), b4=40,6 и b9=1299,2. Найдите формулу n-го члена.
-
Катя поступила на работу официанткой в кафе. В первый месяц ее зарплата составляла 3500 р. В каждый следующий месяц зарплата повышалась на 200р. Сколько Катя заработала за год?
-
Числовая последовательность задана формулой n-го члена an=
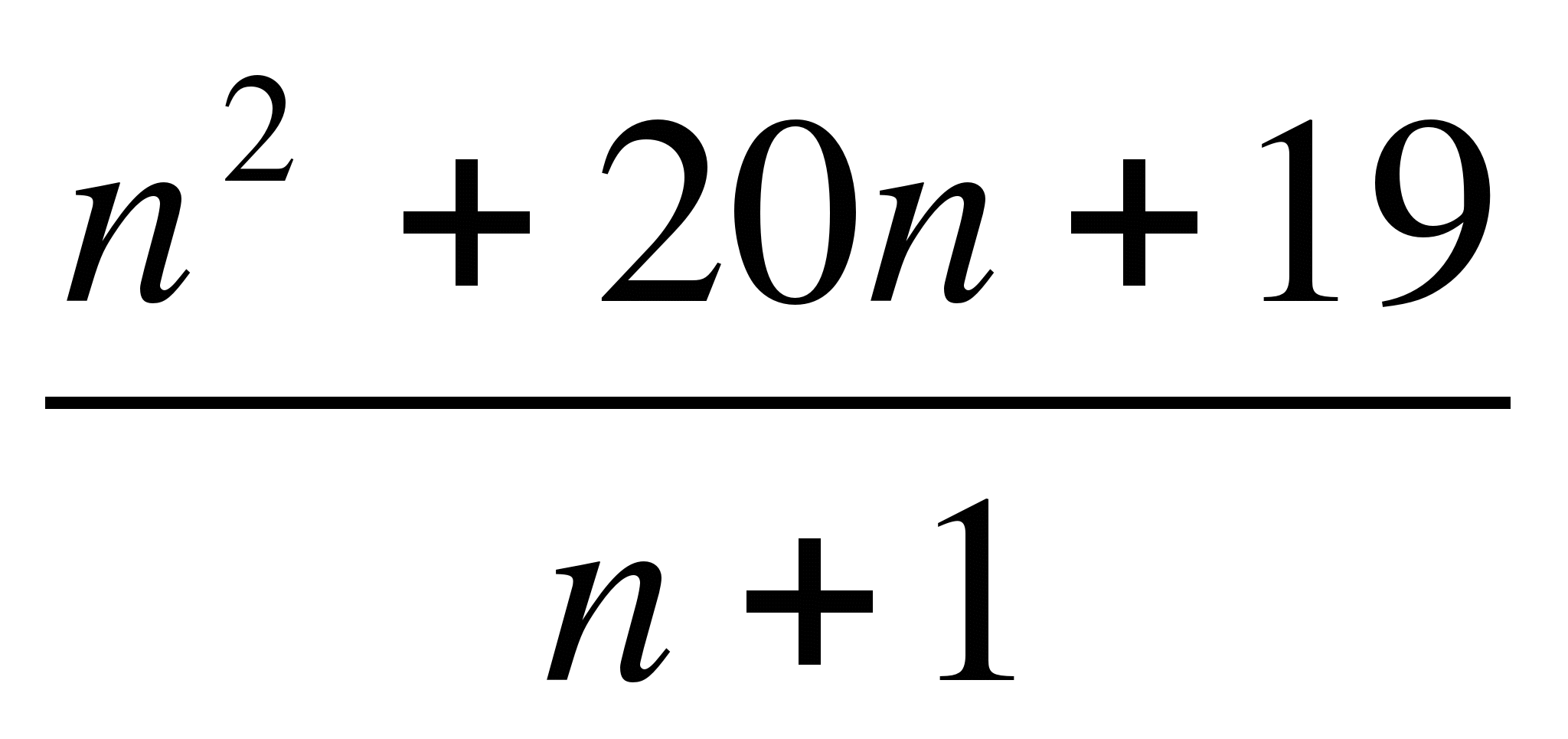 . Найдите номер
члена последовательности равного 26.
. Найдите номер
члена последовательности равного 26.
-
Запишите первые три члена последовательности, заданной формулой n-го члена: an=
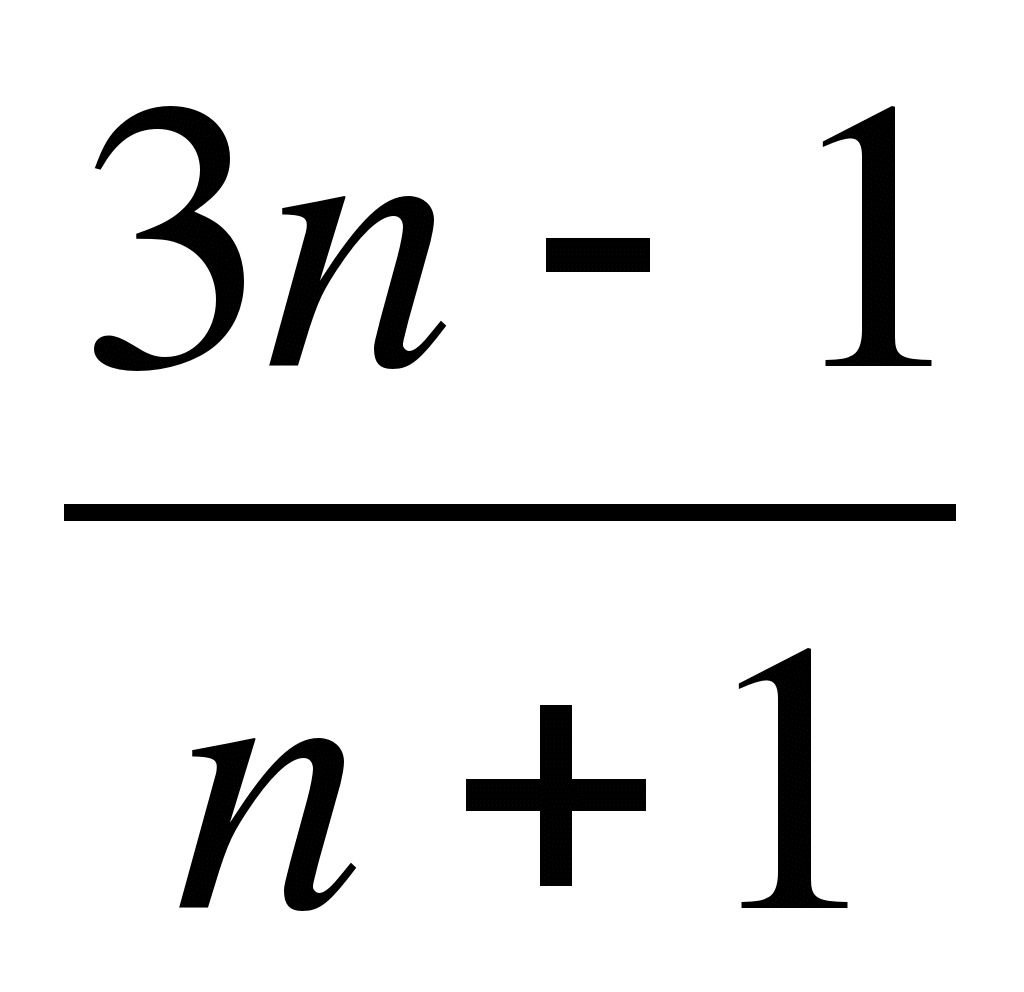 . Одному пропуску
соответствует только одно число.
. Одному пропуску
соответствует только одно число.
-
В геометрической прогрессии найти b3, если b1=0,5; q=-2.
-
Вычислите сумму 30+31+32+…+38+39+40.
-
Найти сумму всех натуральных чисел, кратных 6 и не превосходящих 250.
-
В геометрической прогрессии b1=72
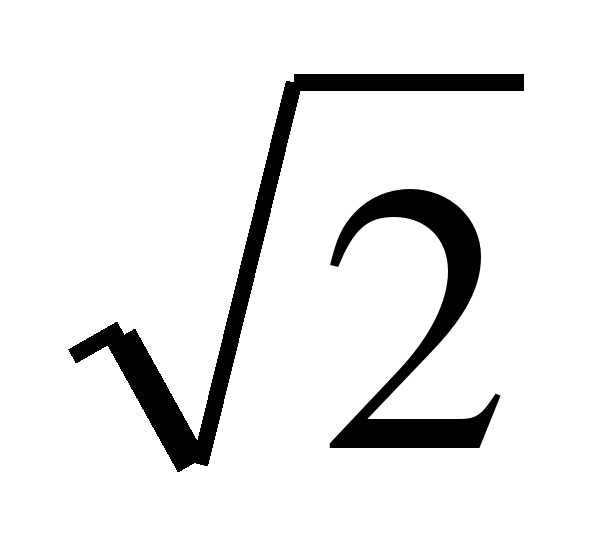 ; b2=8
; b2=8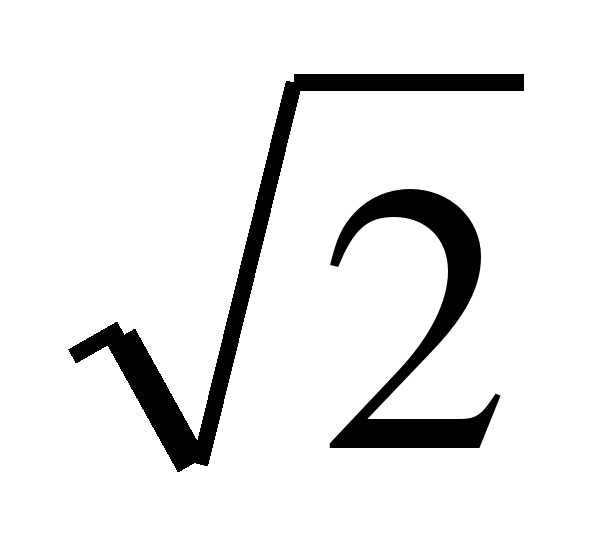 . Найдите q.
. Найдите q.
-
Чему равно число членов арифметической прогрессии -2;2;…меньших 55.
Приложение №3
Тесты с развернутым ответом
-
Найдите сумму всех отрицательных членов арифметической прогрессии -6,8;-6,6;…
-
В геометрической прогрессии b3=
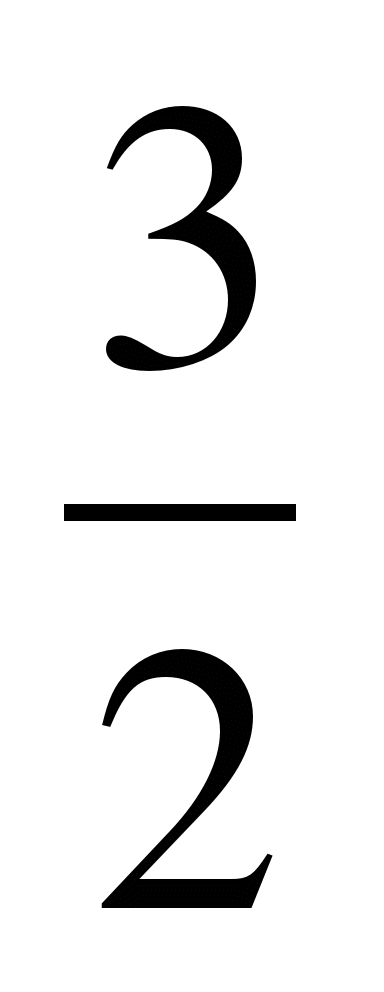 , b6=12 есть ли
среди членов этой прогрессии число 144?
, b6=12 есть ли
среди членов этой прогрессии число 144?
-
Две последовательности заданы формулами своих отрицательных членов: xk=7k-2, ym=5m-2. Найдите наименьшее из чисел, являющимися членами обеих последовательностей.
-
В геометрической последовательности сумма первого и второго членов равна 108, а сумма второго и третьего членов 135. Найдите первые три члена этой прогрессии.
-
Найдите сумму всех отрицательных чисел арифметической прогрессии -7,2;-6,9;…
-
В 1-ы день магазин продал 12кг сахара, а в каждый следующий день продавал на 2кг сахара больше, чем в предыдущей. Сколько сахара продал магазин за 8 дней?
-
Составит формулу n-го члена, если разность между пятым и третьим членом равно 144, а разность между четвертым и вторым равна 48.
-
В равносторонний треугольник со стороной 8см вписан другой треугольник, вершинами которого являются середины сторон первого. Во второй треугольник таким же образом вписан третий треугольник и т. Д. Найдите периметр восьмого треугольника.
-
Все члены геометрической прогрессии (bn) различны. Между b2 и b3 можно вставить число х так, что числа b1, b2, х и b3 составляют арифметическую прогрессию. Найдите знаменатель геометрической прогрессии.
-
Четыре числа составляют геометрическую прогрессию. Найти эти числа, если известно, что при увеличении их на 10, 11, 9 и 1 соответственно они составляют арифметическую прогрессию.
-
В окружность радиусом 4 см вписан квадрат, в который снова вписана окружность и т. Д. Найдите сумму всех таких окружностей.
-
Дана геометрическая прогрессия (Cn) с положительными членами, в которой С4=24, С6=96. Найдите С1 и определите количество членов прогрессии, начиная с первого, сумма которых равна 45.
-
Сумма первых трех членов геометрической прогрессии равна 26, а сумма следующих трех членов равна 702. Составьте формулу n-го члена. Найдите сумму первых пяти членов.
-
В арифметической прогрессии (аn) а1=111, d=-6. Какое наименьшее число членов этой прогрессии, начиная с первого, нужно взять, чтобы их сумма была отрицательной.
-
Найдите значение х, при котором х-1; 4х-3 и х2+1 составляют арифметическую прогрессию.
-
Дана арифметическая прогрессия (аn), в которой а2*а5=112,

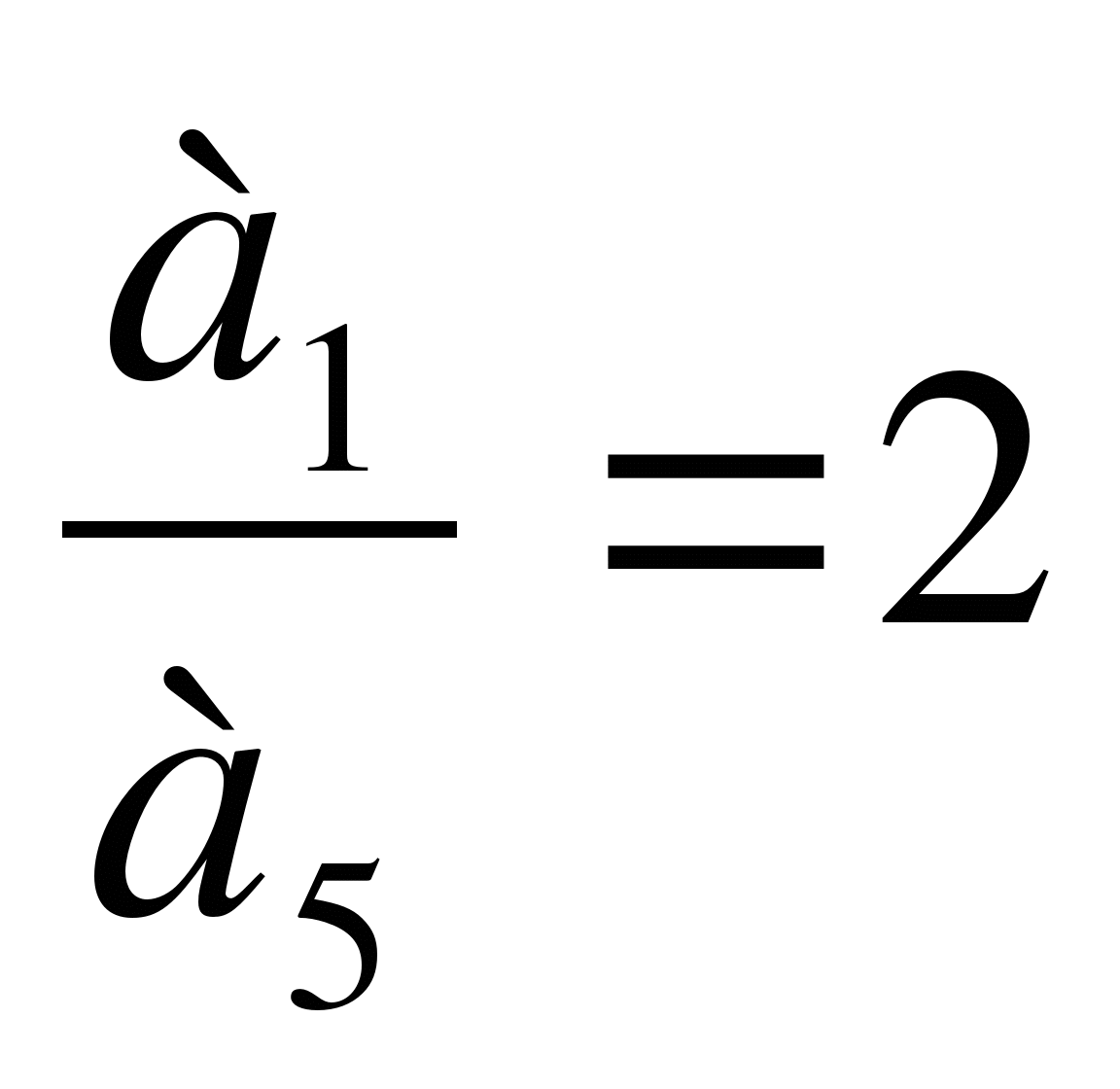 . Составьте формулу n-го
члена данной прогрессии. Определите, сколько в данной
прогрессии членов, модуль которых не превосходит 70.
. Составьте формулу n-го
члена данной прогрессии. Определите, сколько в данной
прогрессии членов, модуль которых не превосходит 70.
-
Дана последовательность двузначных натуральных чисел кратных 4. Составьте формулу суммы первых n членов дано последовательности. Найдите сумму двузначных натуральных чисел, не кратных 4.
-
Арифметическая последовательность содержит 10 членов, а ее разность равна 5. На сколько сумма членов с четными номерами отличается от суммы членов с нечетными номерами.
-
Найдите четыре числа, из которых первые три составляют арифметическую прогрессию, а последние три - геометрическую, если сумма крайних чисел равна 7, а сумма средних чисел равна 6.
-
Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы их сумма была больше 120?
-
Если к задуманному целому числу прибавить 3 и эту сумму разделить на 5, то полученное частное будет больше 8. А если из того же задуманного числа вычесть 7 и эту разность разделить на 4, то полученное частное будет меньше 8. Какое число было задумано?
-
Основание равнобедренного треугольника равно 21см, а его периметр меньше 55см. Какую длину может иметь боковая сторона?
Приложение №4
Тесты с выбором ответа: «правильно»/ «неправильно», «да»/ «нет».
-
Последовательность задана формулой
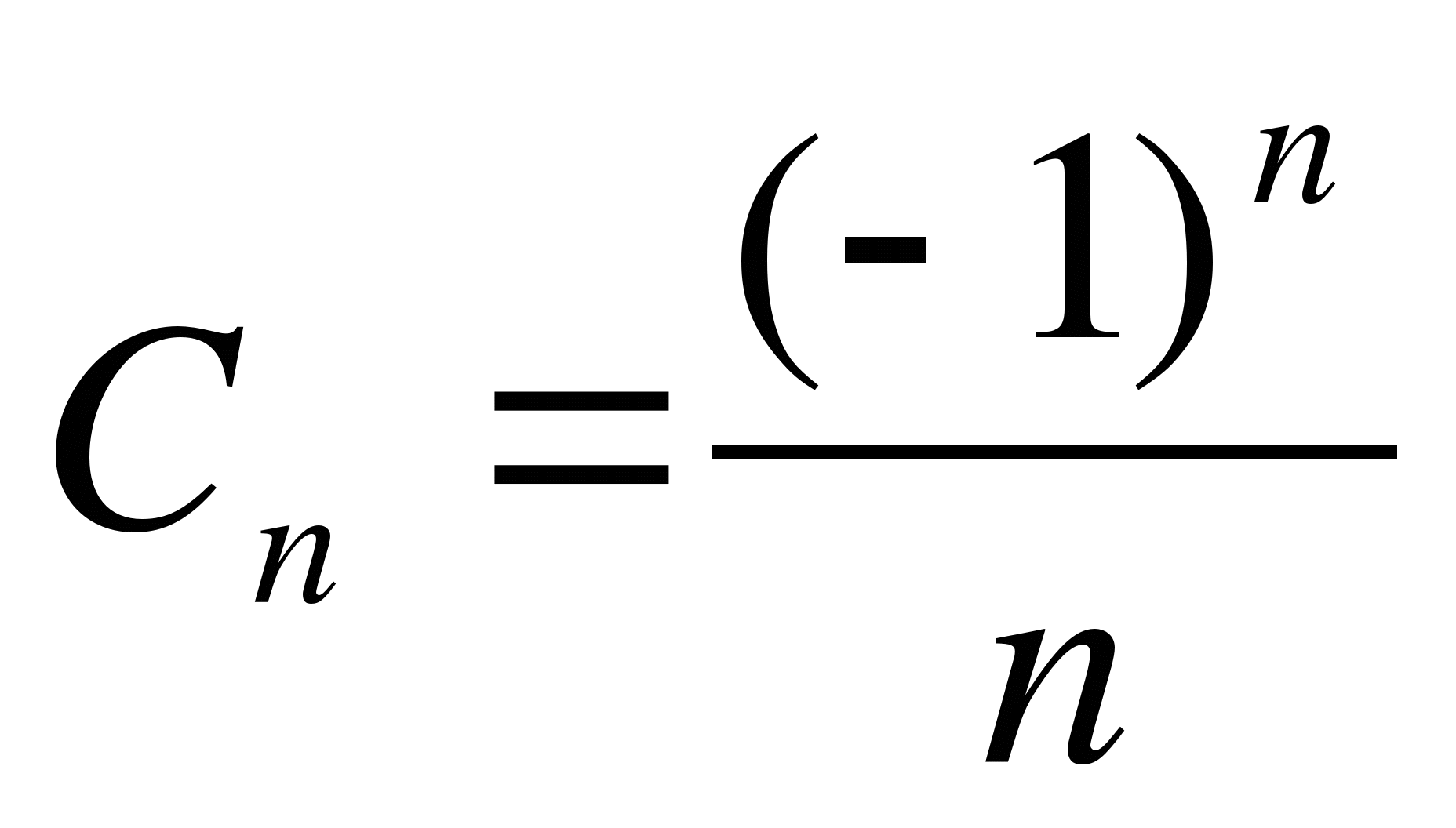 . Является ли член этой
последовательности
. Является ли член этой
последовательности 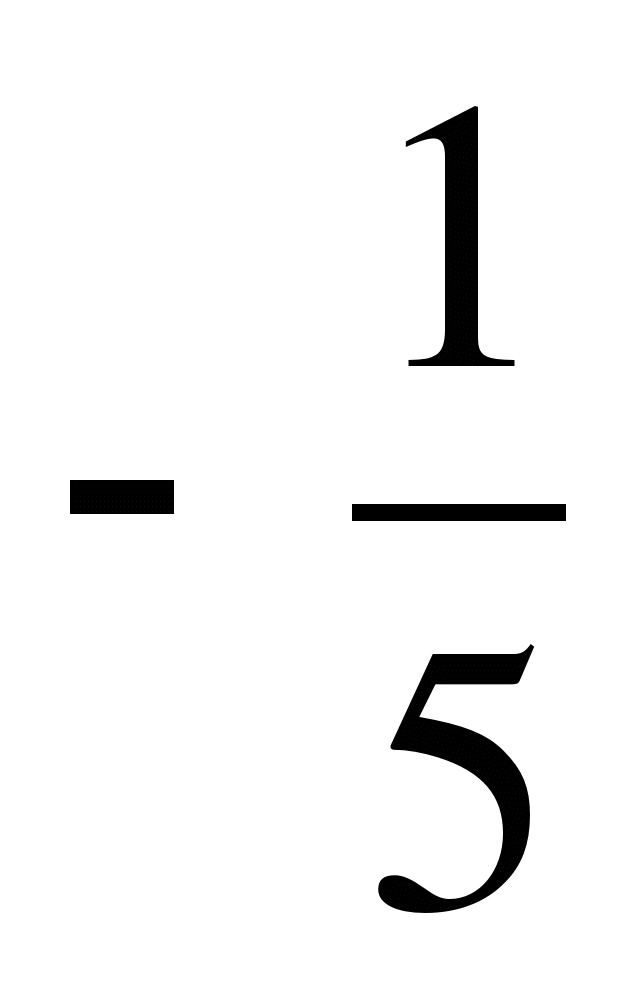 ?
?
1) да 2) нет
-
Является ли последовательность арифметической прогрессией:
а) 3,6,9,12,…
б) 2,4,8,16,…
в) 10,7,4,1,…
г) 100,1,0,1,…
1) да 2) нет
-
Дана арифметическая прогрессия 3,6,9,12,…, разность которой равна 3.
1) правильно 2) неправильно
-
Является ли последовательность -40,-20,0 арифметической прогрессией?
1)нет 2) да
-
Является ли последовательность 4,19,24, геометрической прогрессией?
1) да 2) нет
-
Дана арифметическая прогрессия
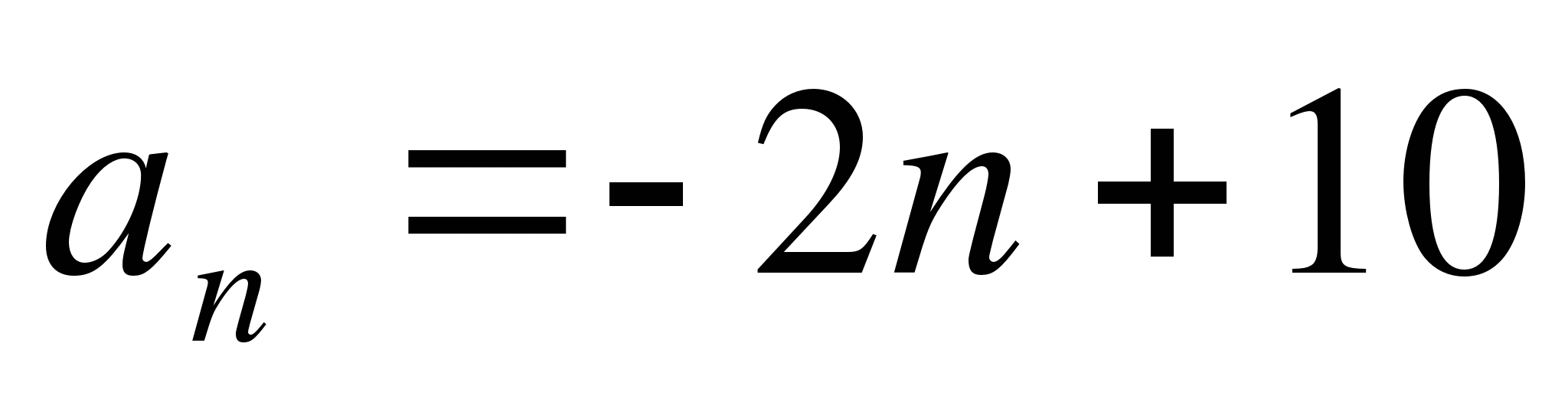 , заданная формулой n-го
члена. Выполняется ли для неё условие
, заданная формулой n-го
члена. Выполняется ли для неё условие 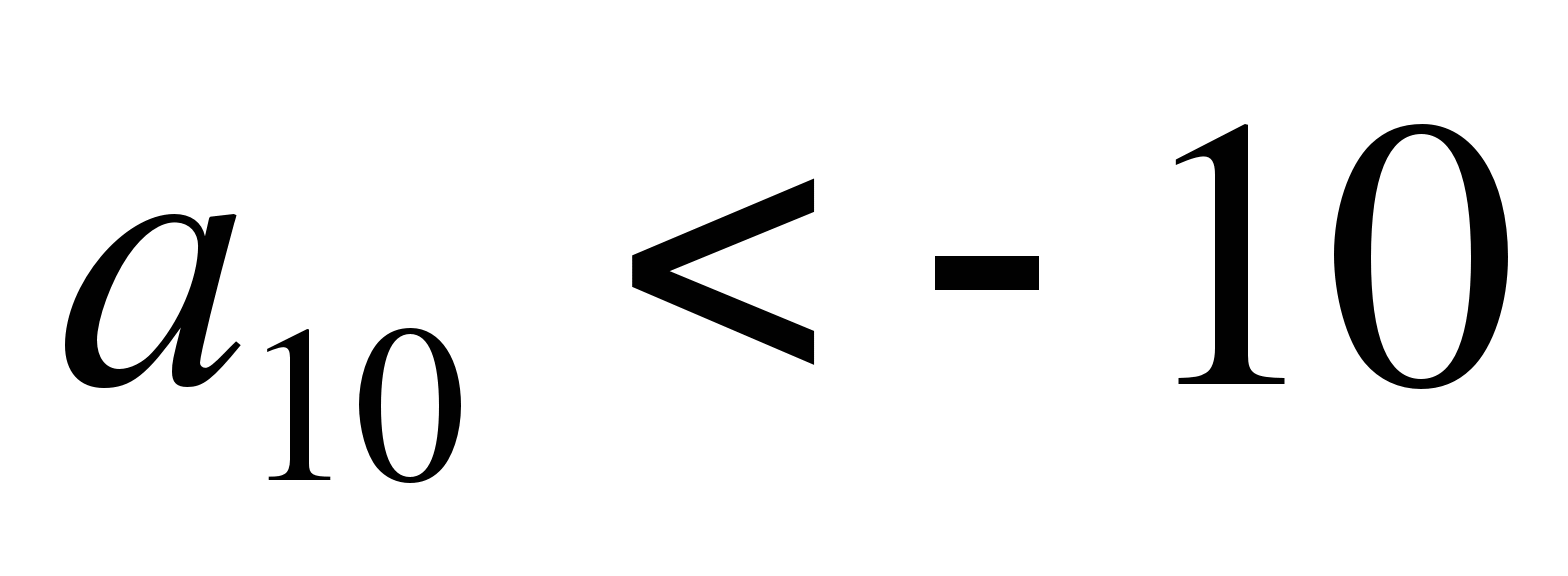 ?
?
1) нет 2) да
-
Дана арифметическая прогрессия
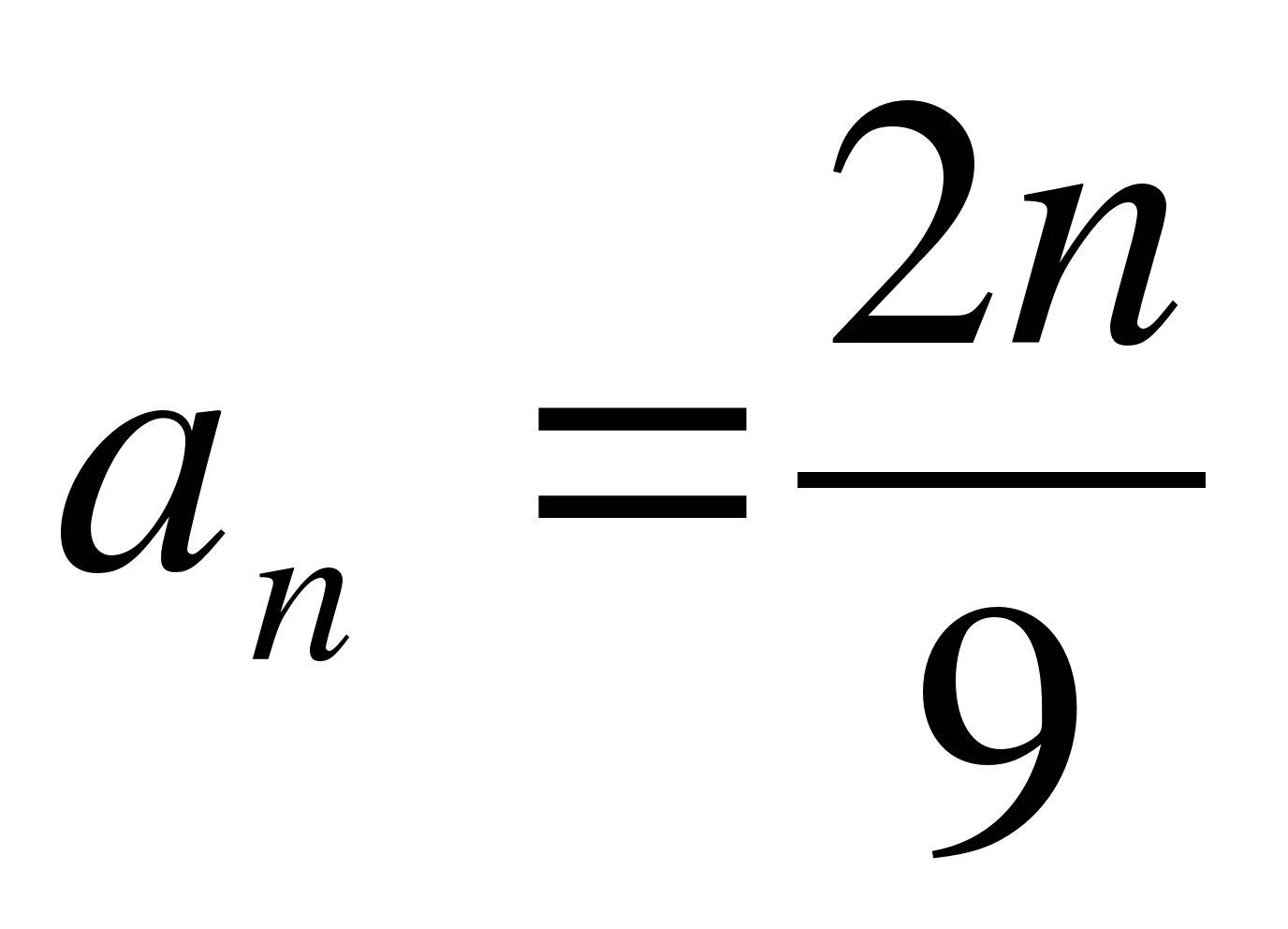 , заданной формулой n-го
члена. Выполняется ли для неё условие
, заданной формулой n-го
члена. Выполняется ли для неё условие 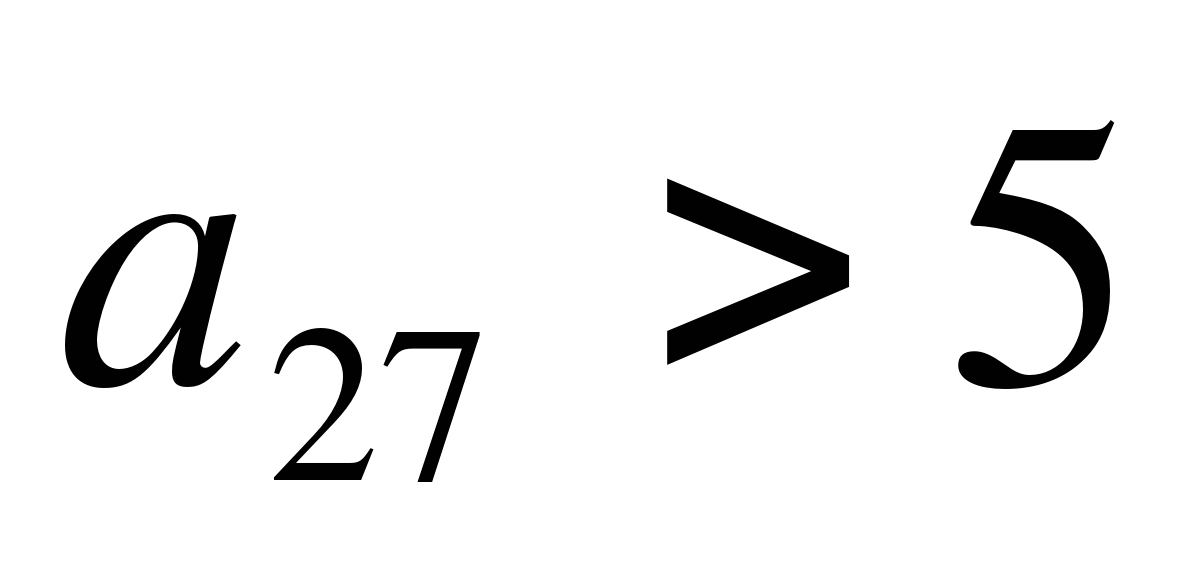 ?
?
1) да 2) нет
-
Последовательность задана несколькими членами. Является ли она возрастающей арифметической? 4,6,8,10
1) да 2) нет
-
Последовательность задана несколькими членами. Является ли она возрастающей геометрической? 1,3,9,27
1) нет 2) да
-
Правильно ли составлена формула суммы 20 членов арифметической прогрессии
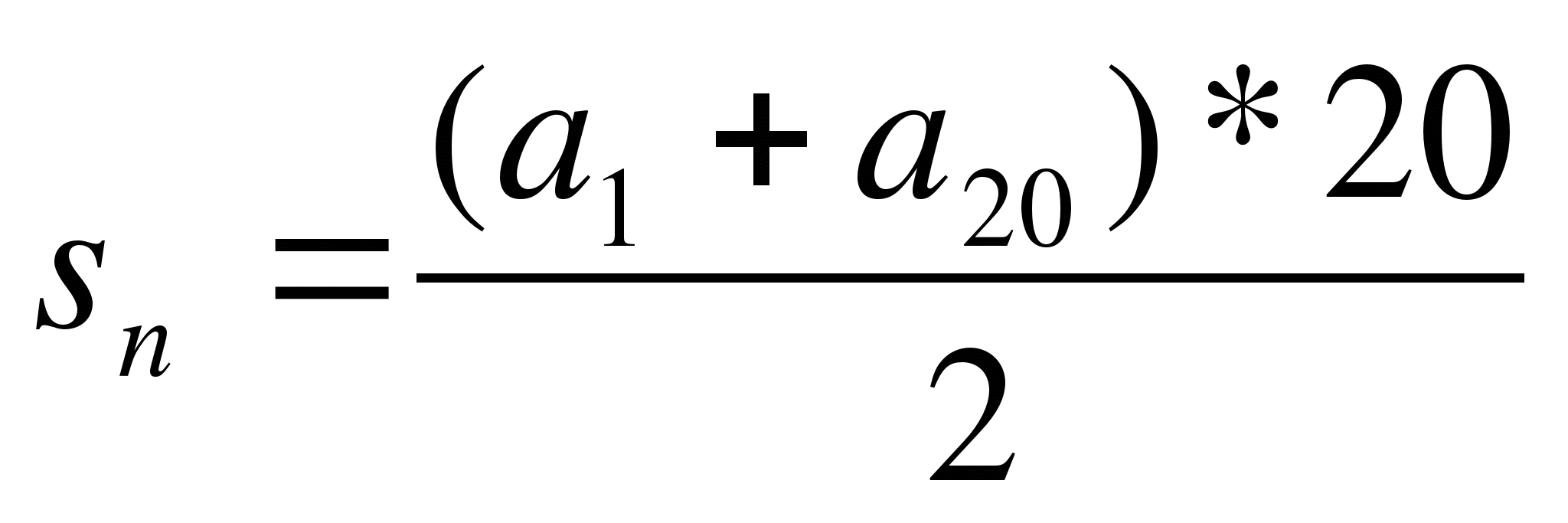 ?
?
1) нет 2) да
-
Пусть (аn) - некоторая арифметическая прогрессия. Является ли геометрической прогрессией последовательность
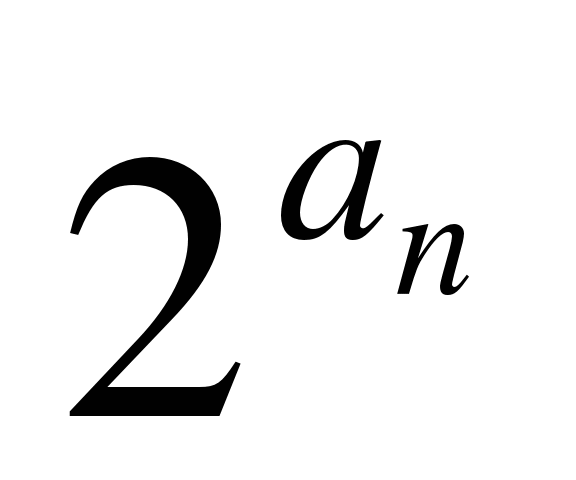 ?
?
1) нет 2) да
-
Есть ли среди членов данной геометрической прогрессии
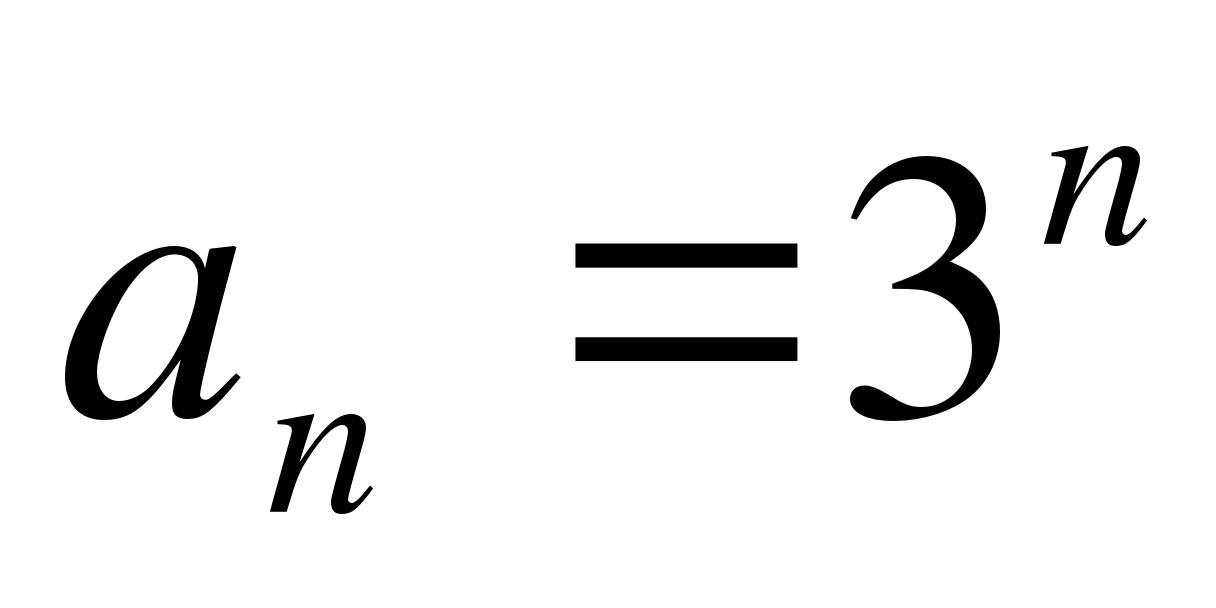 число 9?
число 9?
1) нет 2) да
-
Есть ли среди членов данной арифметической прогрессии
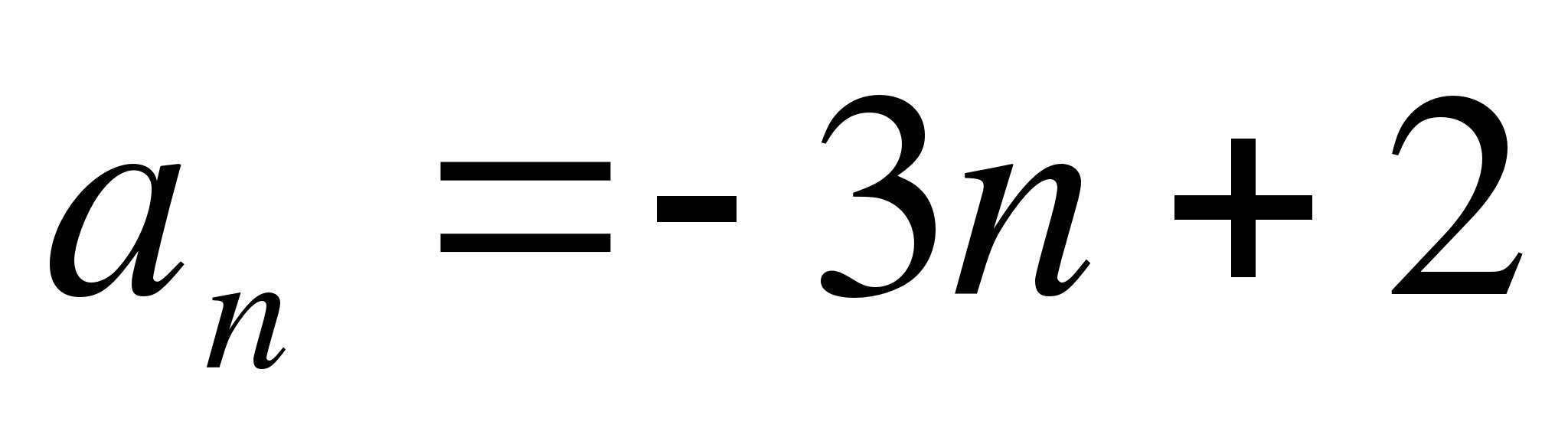 число -10?
число -10?
1) да 2) нет
-
Последовательность задана формулой
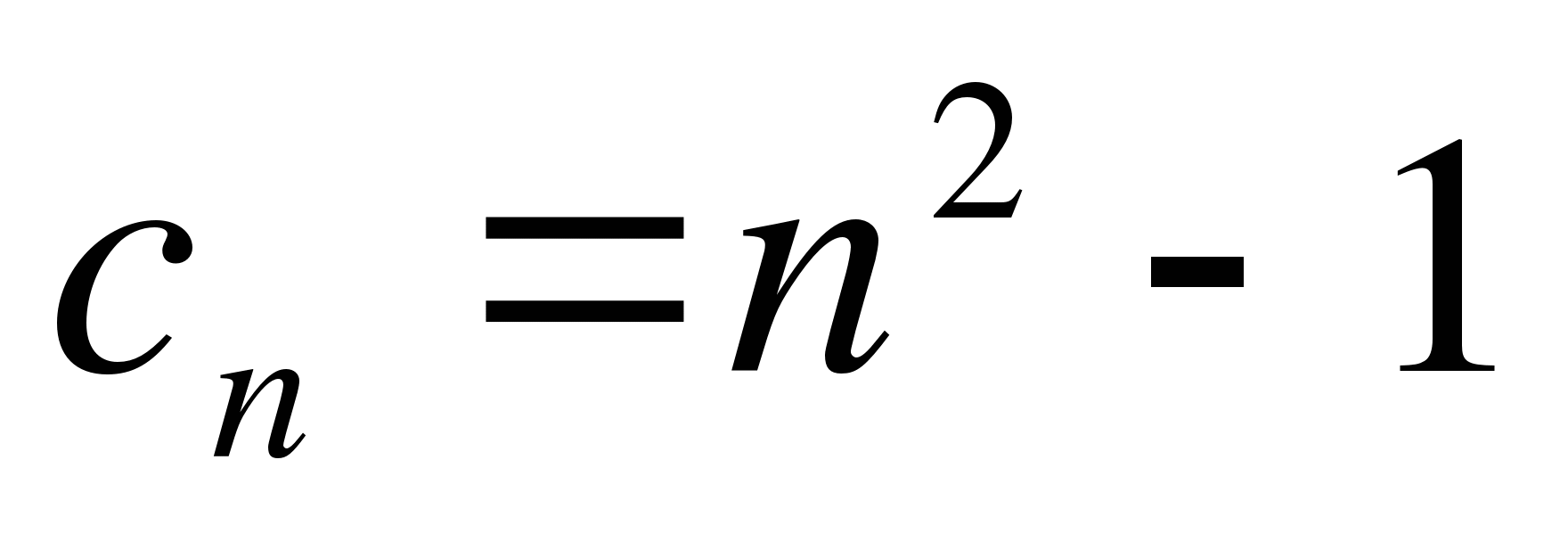 . Является ли число 7 членом
этой последовательности?
. Является ли число 7 членом
этой последовательности?
1) нет 2) да
-
Арифметическая прогрессия задана условиями
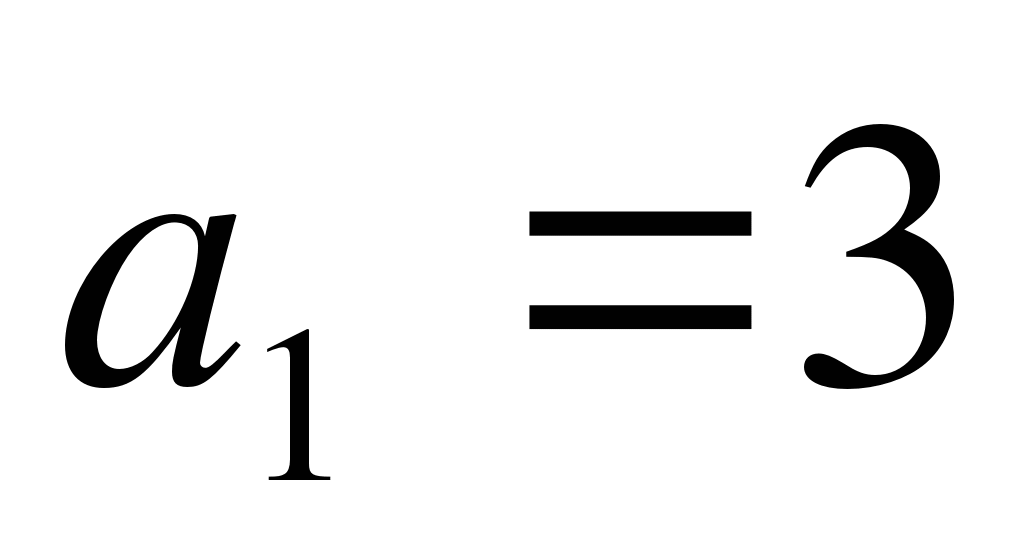 ,
, 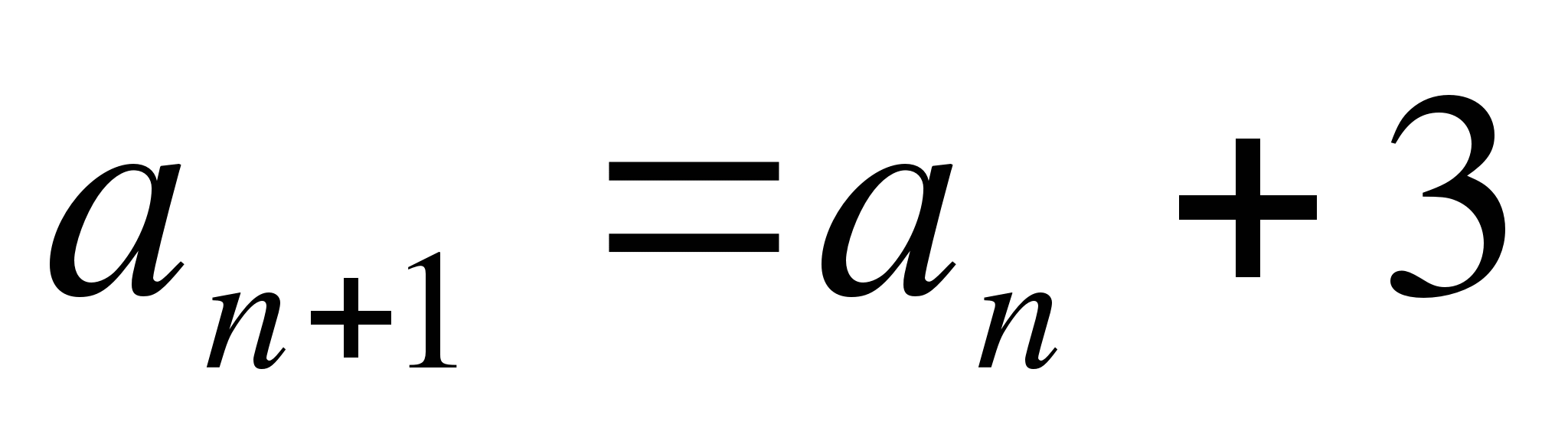 . Является ли число 18
членом этой прогрессии?
. Является ли число 18
членом этой прогрессии?
1) да 2) нет
-
Является ли формула
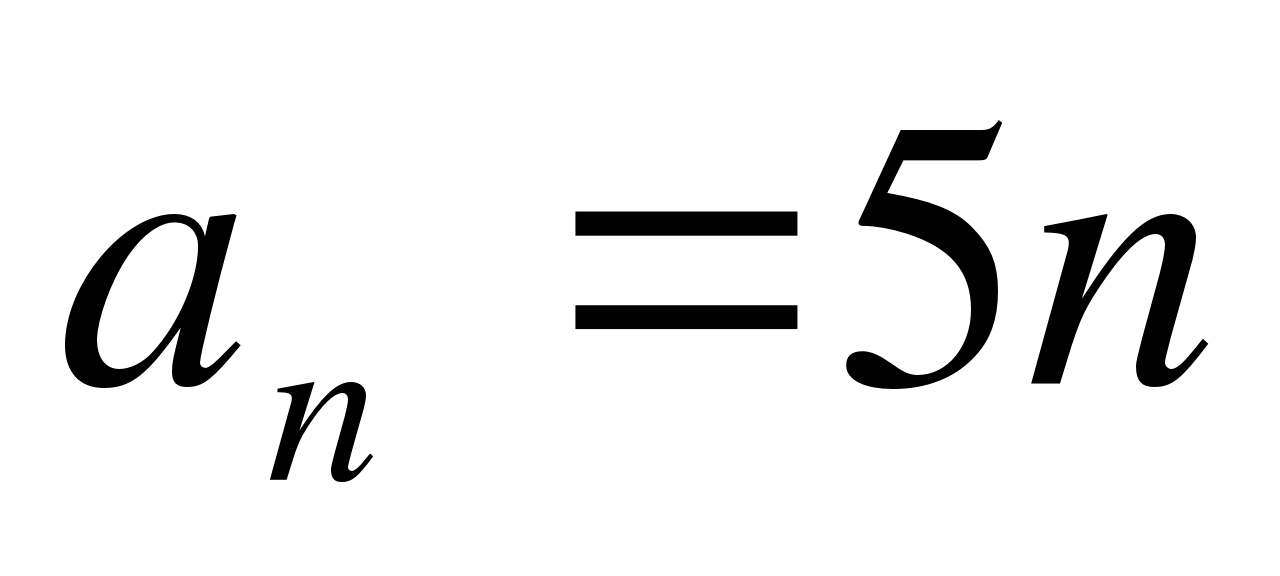 ,
задающая число а, кратной пяти (n - нат. Число)?
,
задающая число а, кратной пяти (n - нат. Число)?
1) да 2) нет
-
Является ли формула
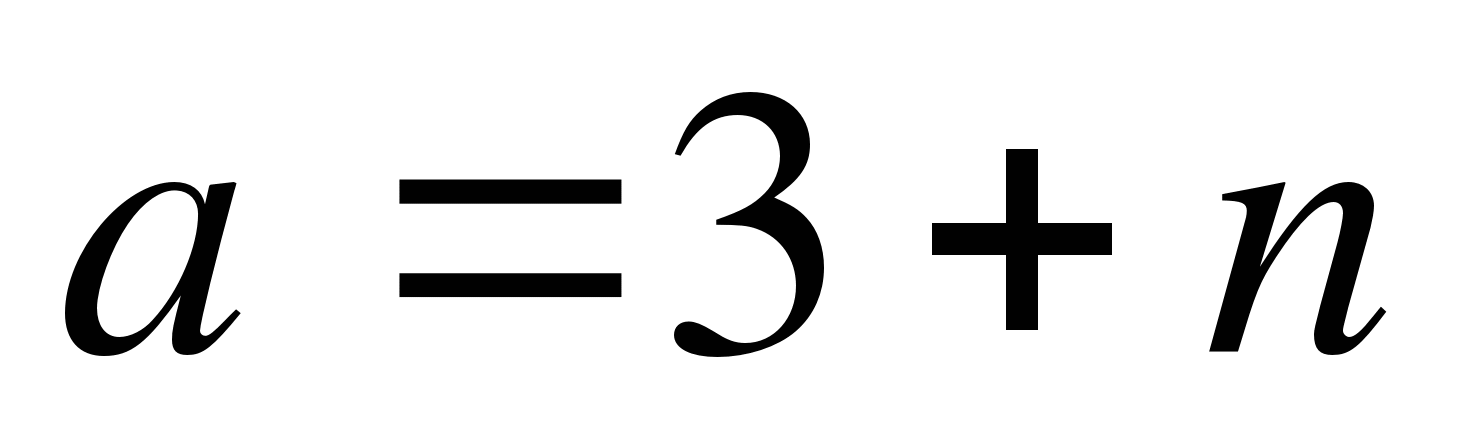 ,
задающая число а, кратное трем ( n - нат. Число)?
,
задающая число а, кратное трем ( n - нат. Число)?
1) нет 2) да
18) Последовательность задана формулой ![]() . Является ли число 484 23
членом этой последовательности?
. Является ли число 484 23
членом этой последовательности?
1) да 2) нет
-
Дана арифметическая прогрессия
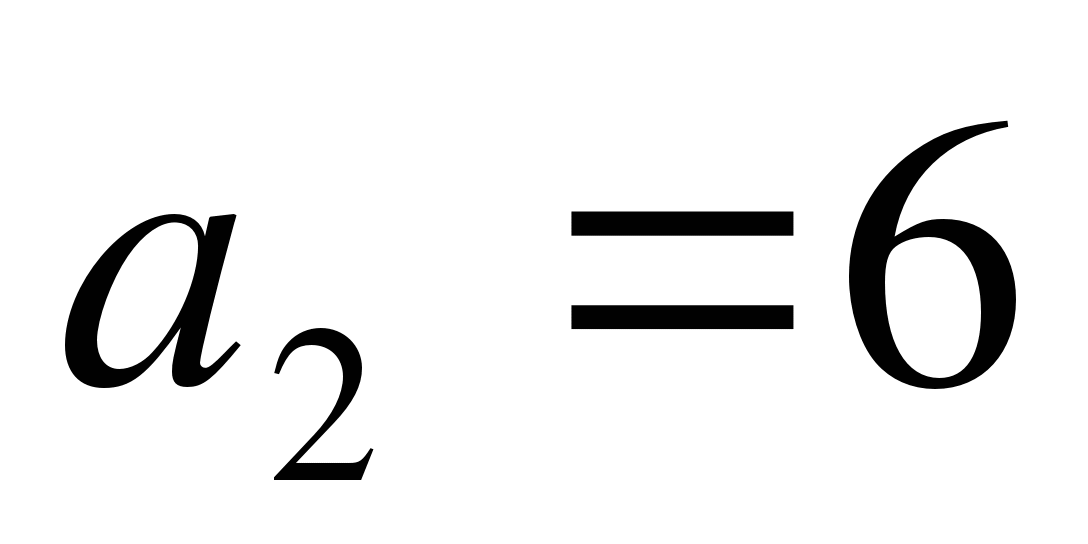 ,
, 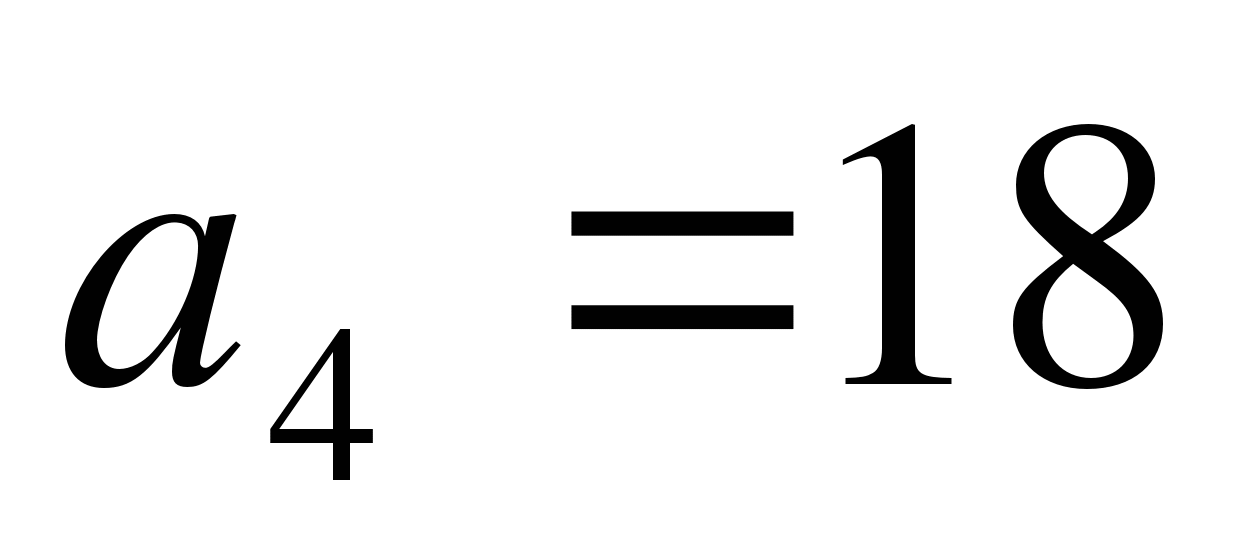 . Может ли
. Может ли 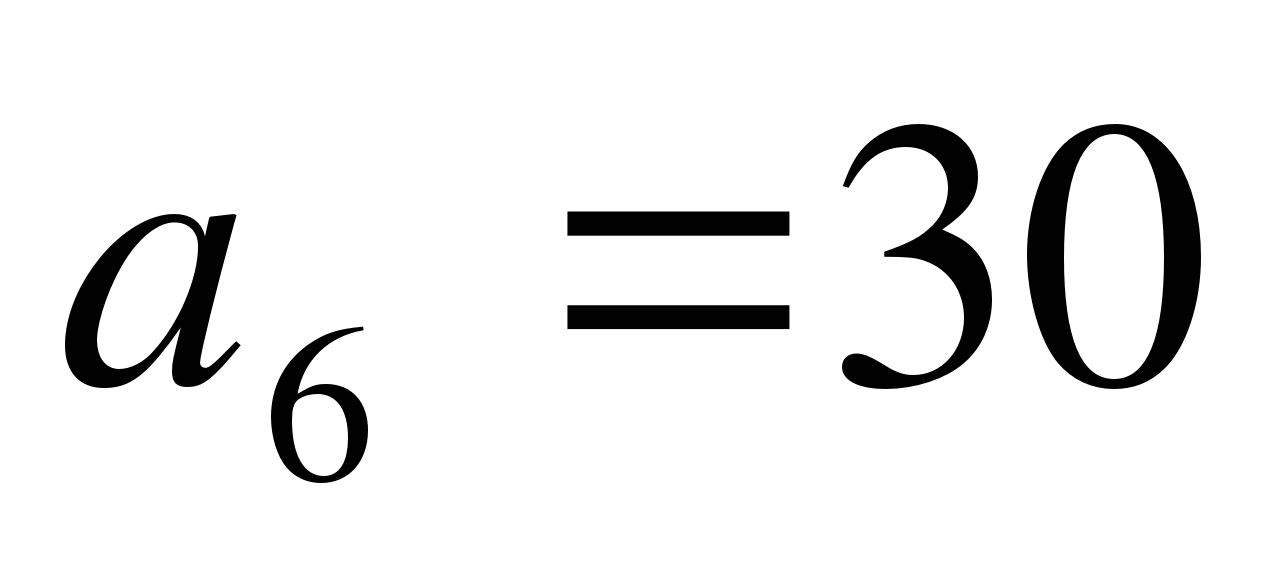 ?
?
1) нет 2) да
Приложение №5
Тесты с множественный выбор
-
Числовая последовательность задана рекуррентной формулой
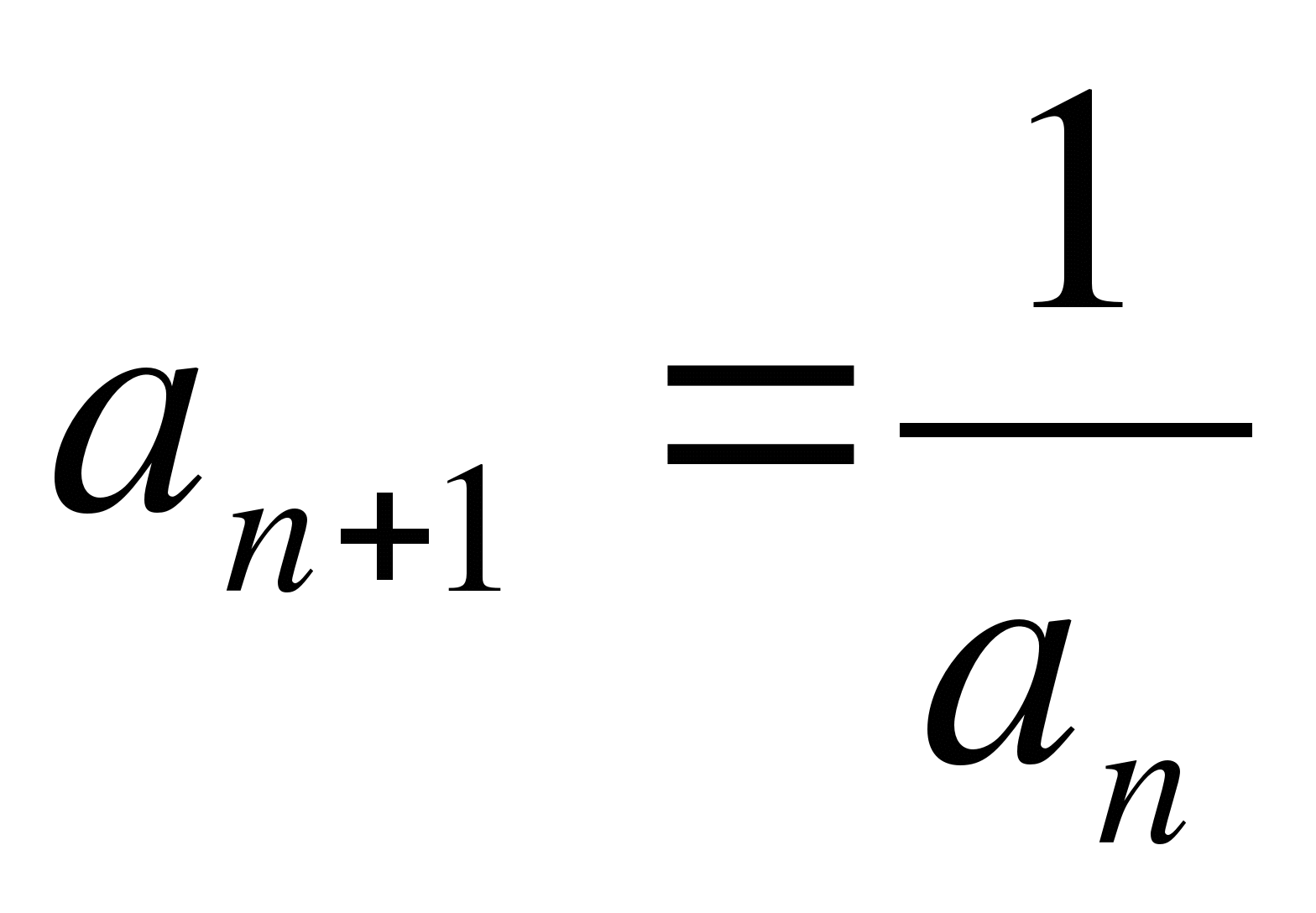 . Найдите пятый член этой
последовательности, если
. Найдите пятый член этой
последовательности, если 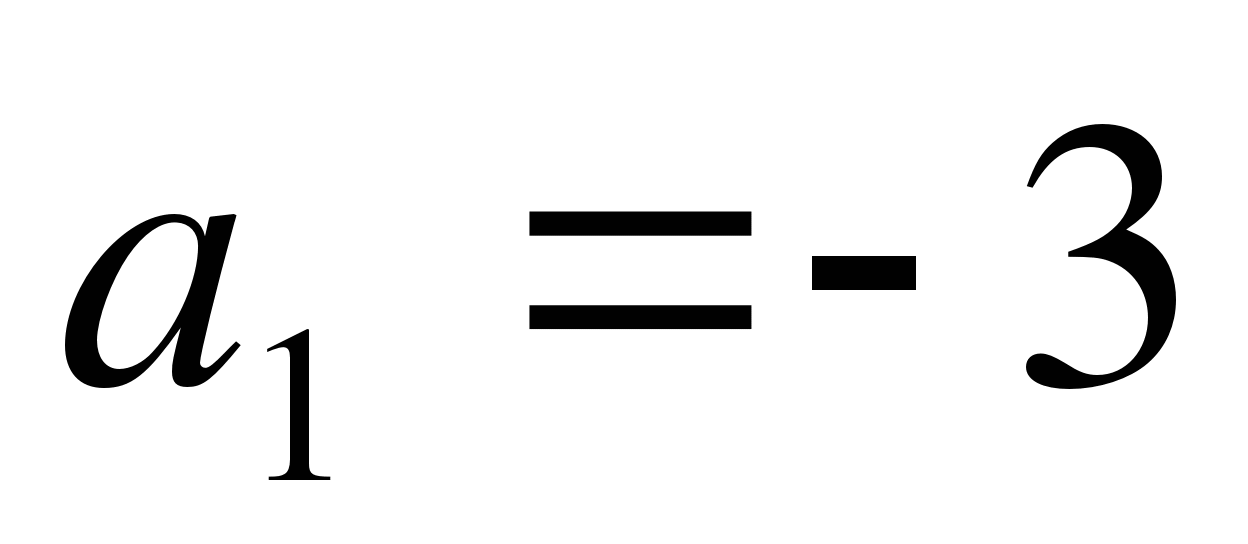 .
.
А) ![]() Б)
Б) ![]() В) 3 Г)
В) 3 Г) ![]()
-
Три положительных числа, первое из которых равно 4, составляют геометрическую прогрессию. Если второе число увеличить на 8, то прогрессия станет арифметической. Найдите знаменатель геометрической прогрессии.
А) 2 Б) ![]() В)
В) ![]() Г)
Г) ![]() Д) 3
Д) 3
-
Найдите три первых члена бесконечной геометрической прогрессии со знаменателем
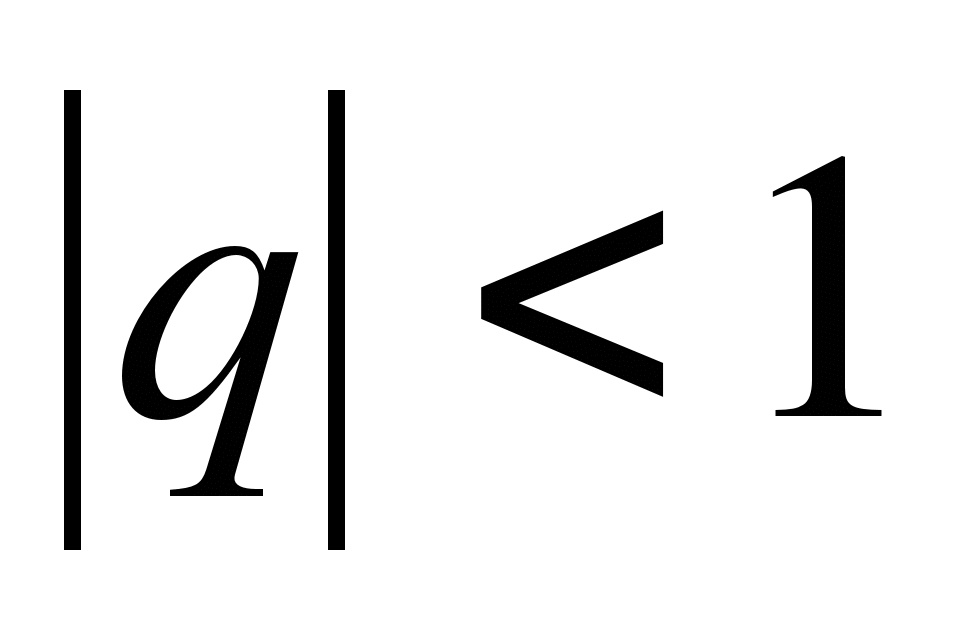 ,
сумма которой равна 6, а сумма пяти первых членов равна
,
сумма которой равна 6, а сумма пяти первых членов равна
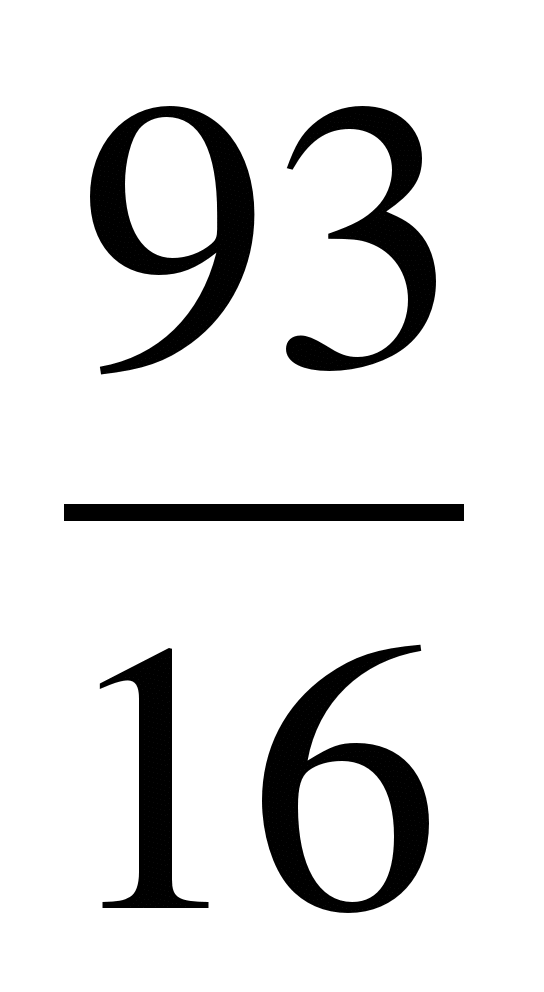 .
.
А) ![]() Б)
Б) ![]() В) 4,2,1 Г)
В) 4,2,1 Г) ![]() Д)
Д) ![]()
-
Сумма членов бесконечно убывающей геометрической прогрессии равна 9, сумма квадратов членов прогрессии равна 40,5. Найдите прогрессию.
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]() Д)
Д) ![]()
-
Выпишите три первые члена арифметической прогрессии, если
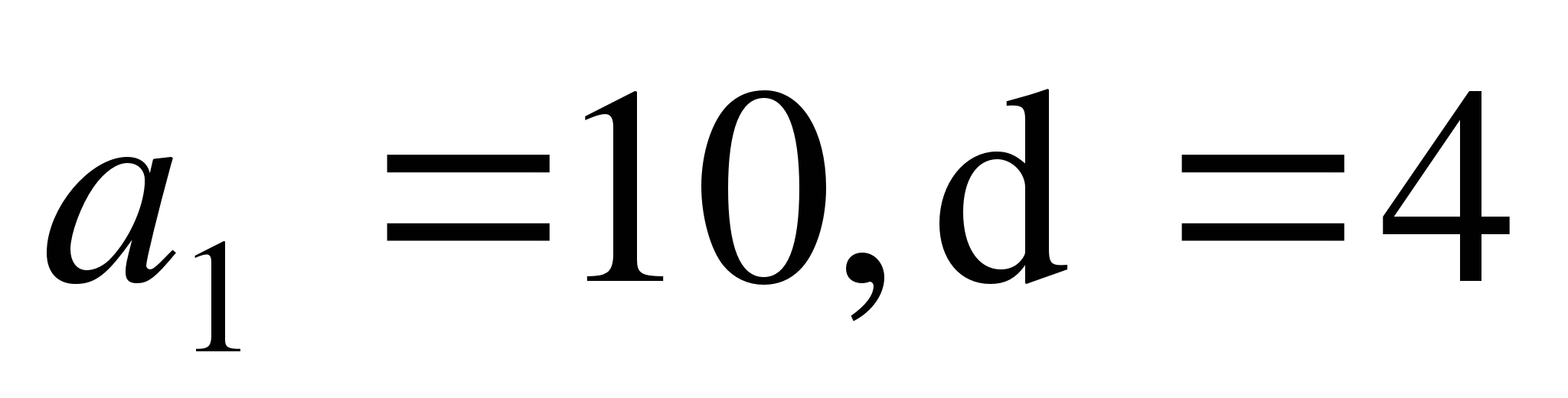 .
.
А) 10,14,18 Б) 10,40,160 В) 10,6,2 Г) Таких чисел нет
-
Последовательность - арифметическая прогрессия. Найдите
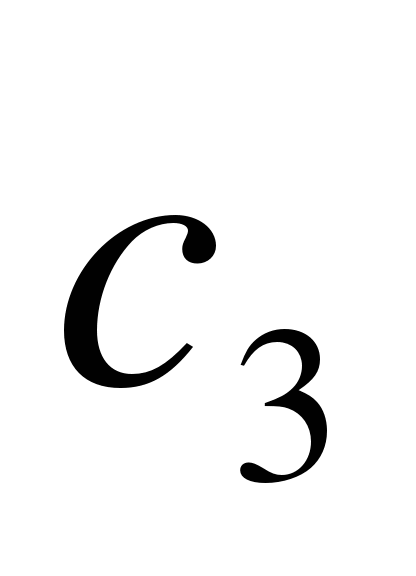 , если
, если 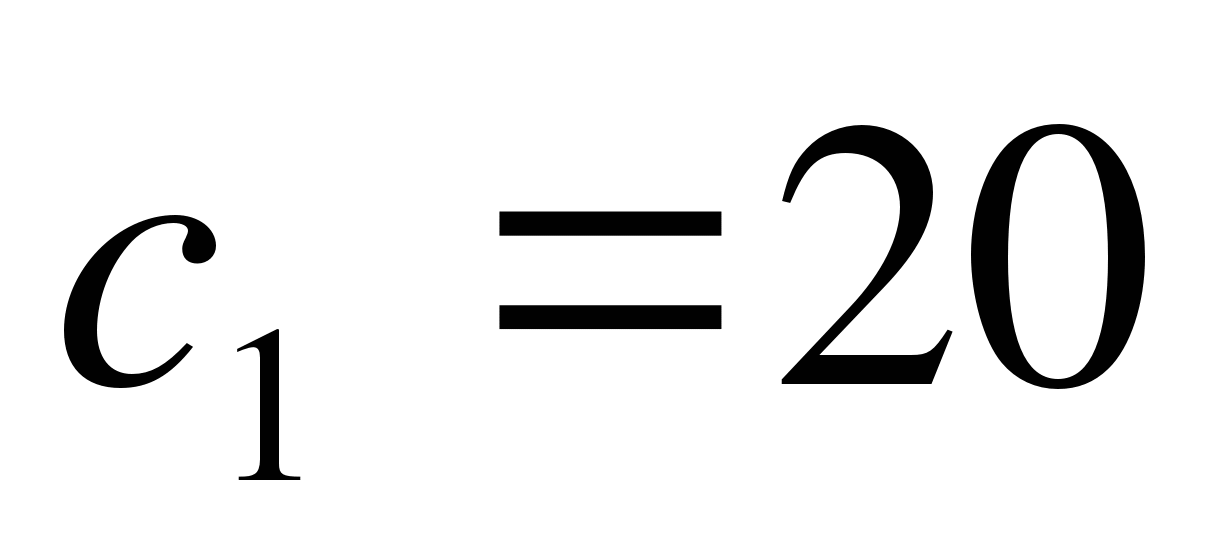 и
и 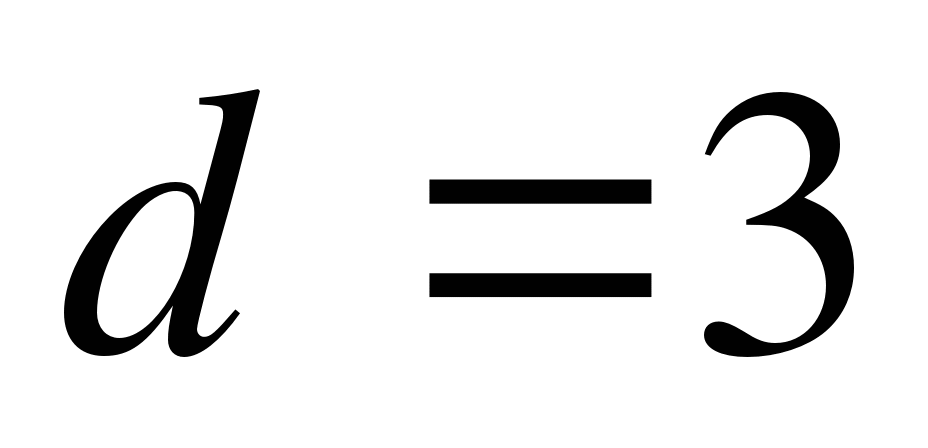 .
.
А) 23 Б) 42 В) 32 Г) 54
-
Найдите четвертый член геометрической прогрессии: 2,-6,…
А) 54 Б) 48 В) ![]() Г) 112
Г) 112
-
Найдите сумму первых сорока членов последовательности, заданной формулой
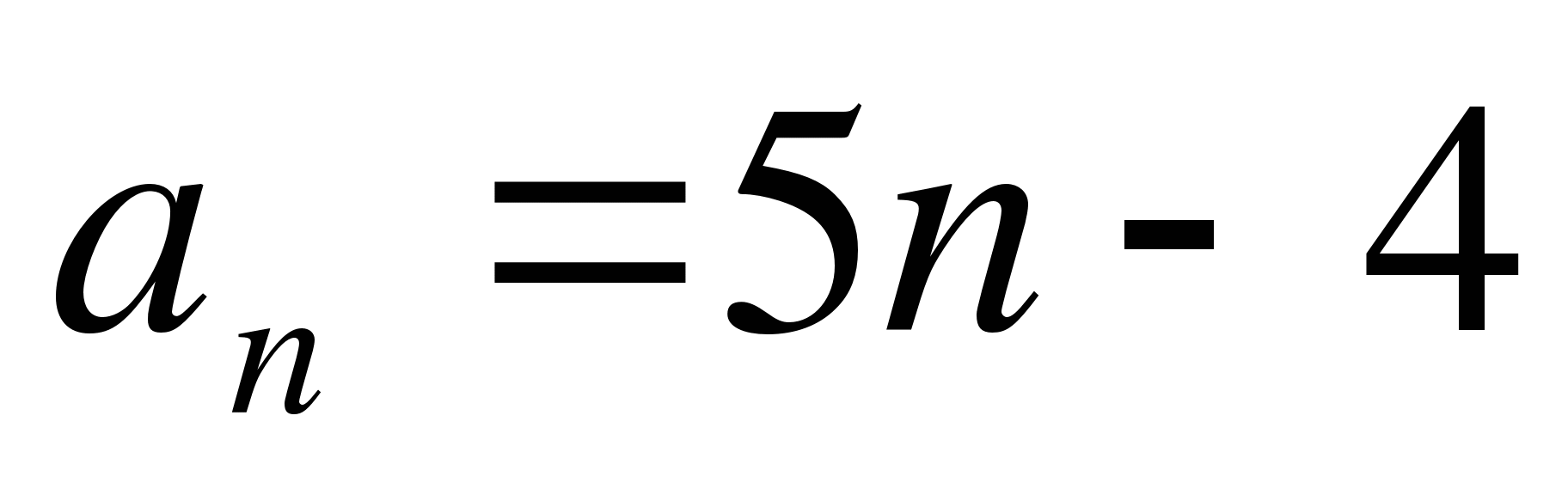 .
.
А) 1280 Б) 6820 В) 125 Г) 3940
-
Последовательность задана формулой
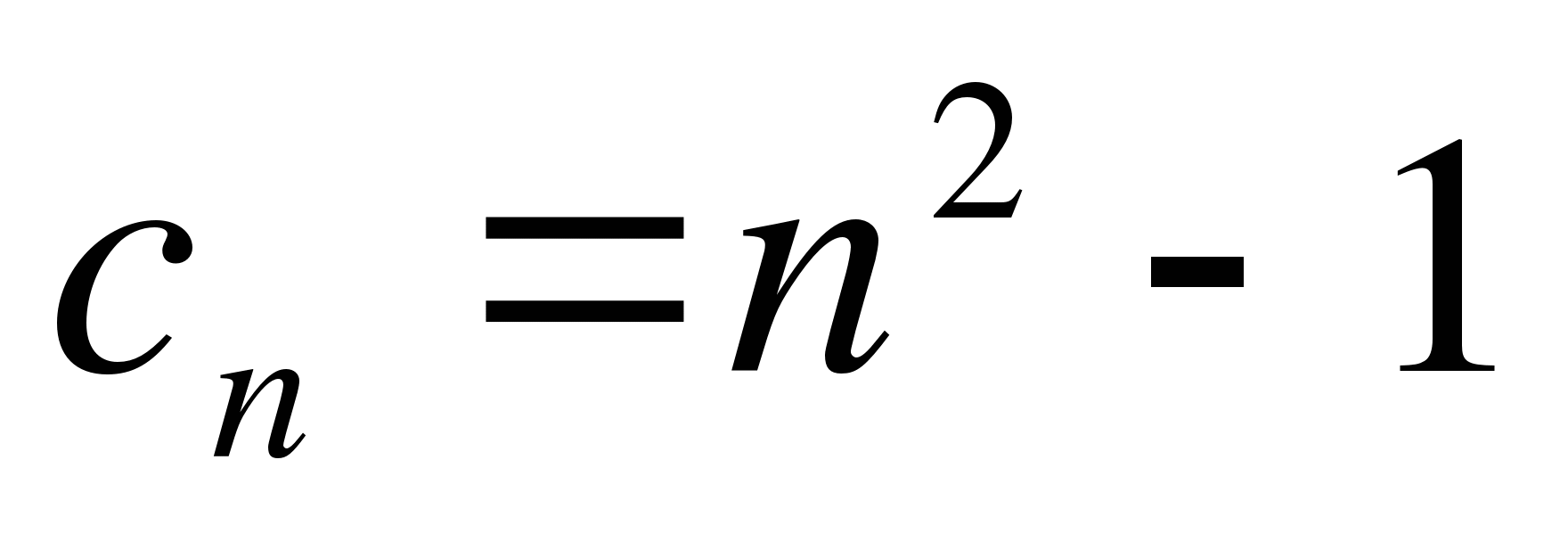 . Какое из указанных чисел
является членом этой последовательности.
. Какое из указанных чисел
является членом этой последовательности.
А 1 Б) 2 В) 3 Г) 4
-
Найти десятый член последовательности, заданной формулой
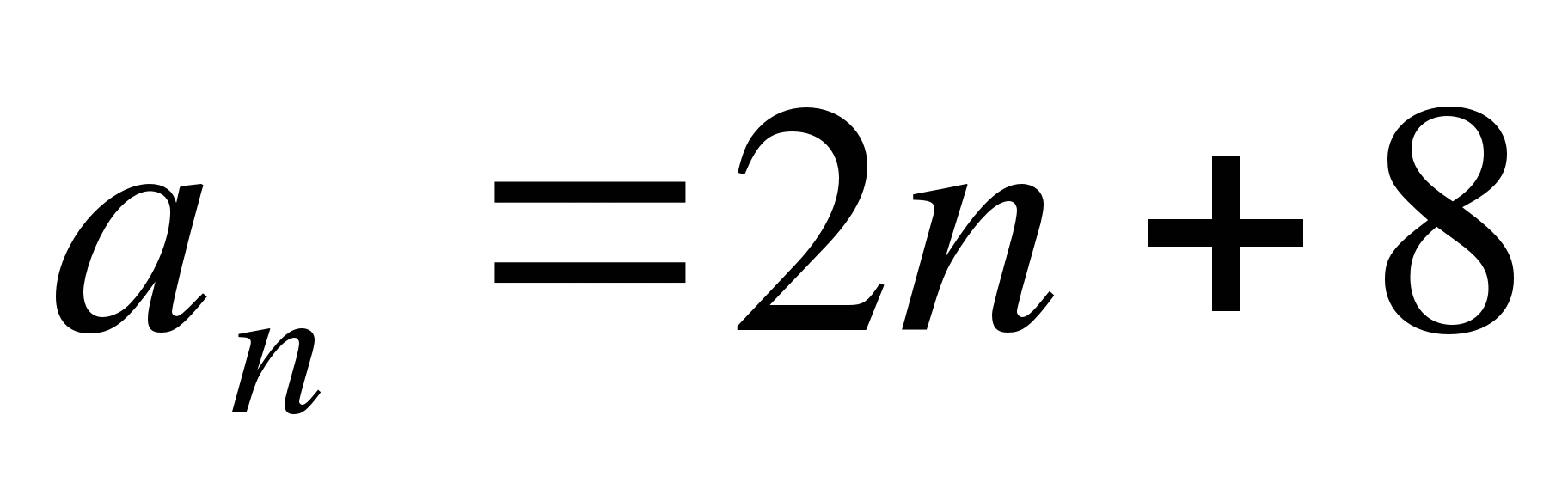 .
.
А) 12 Б) 18 В) 208 Г) 28
-
Положительный знаменатель геометрической прогрессии, в которой
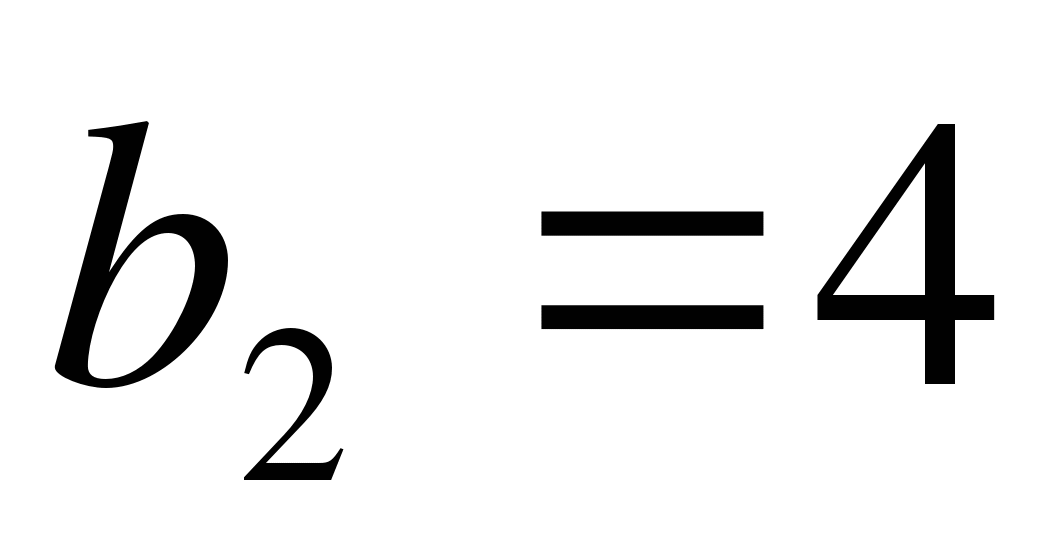 и
и 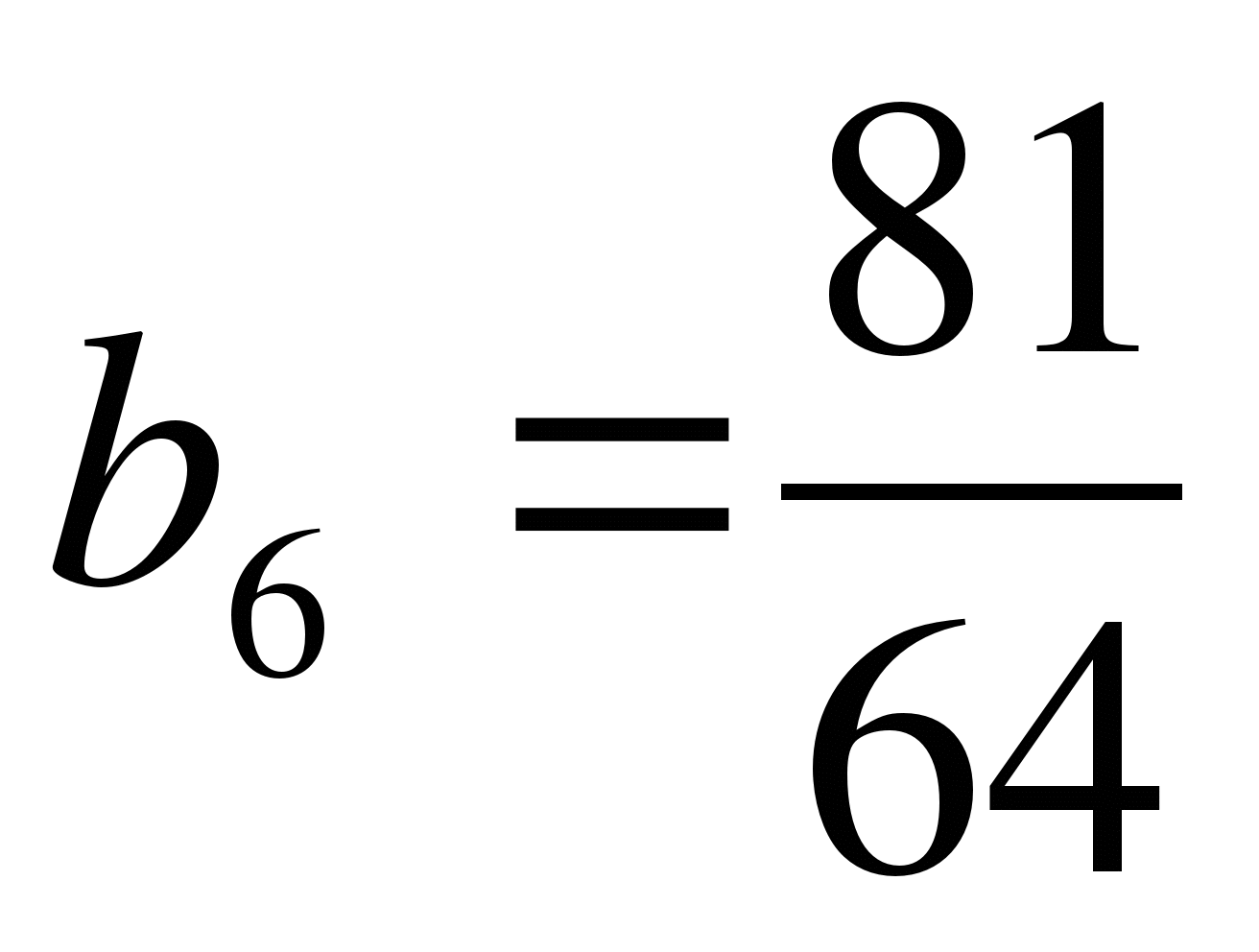 , равен:
, равен:
А) ![]() Б)
Б) ![]() В)
В) ![]()
-
Последовательность задана формулой
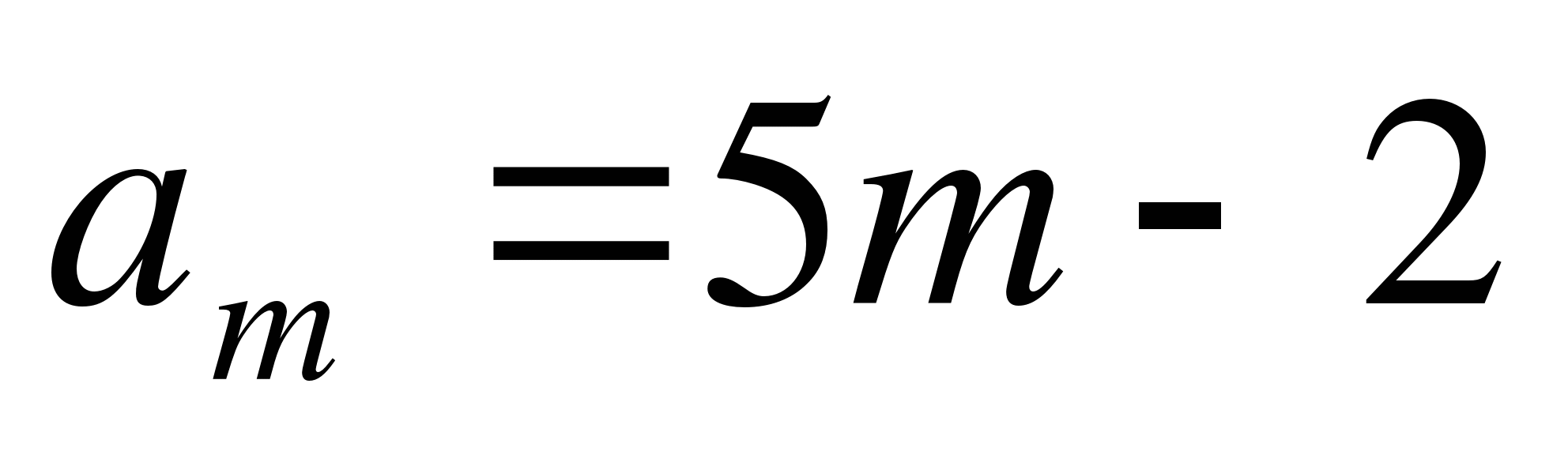 , mє N. Сумма первых её 14
членов равна:
, mє N. Сумма первых её 14
членов равна:
А) 525 Б) 597 В) 497
-
Сумма пяти первых членов геометрической прогрессии, в которой
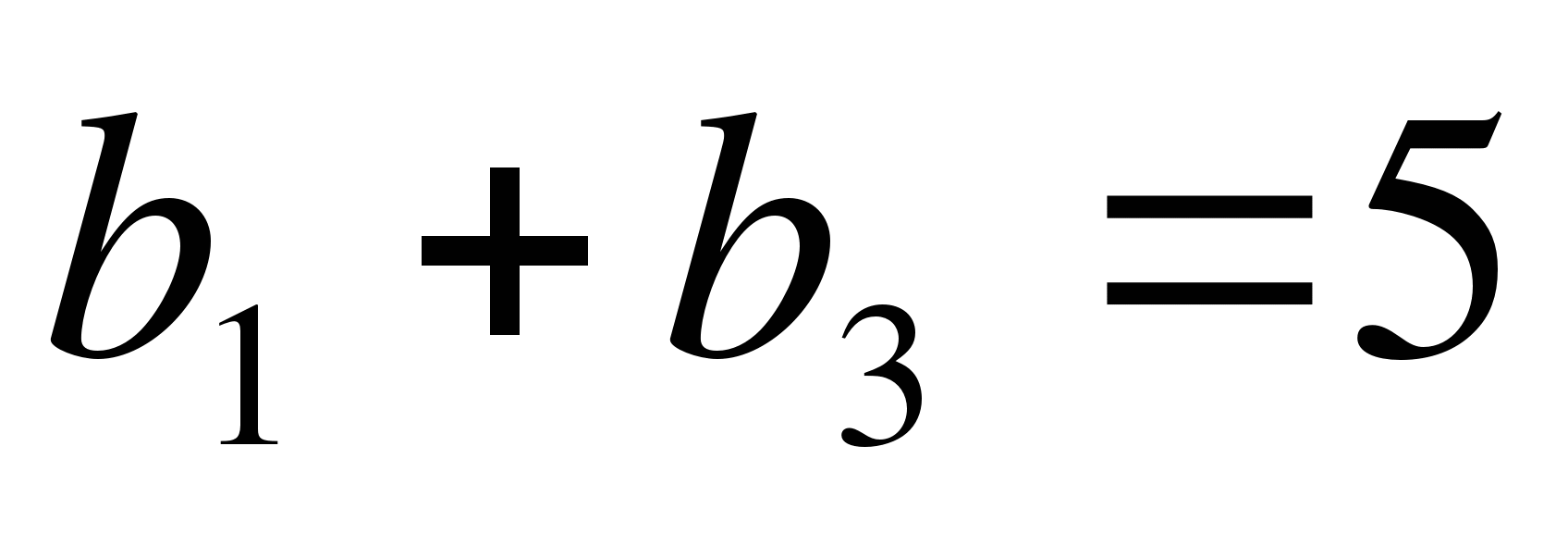 и
и 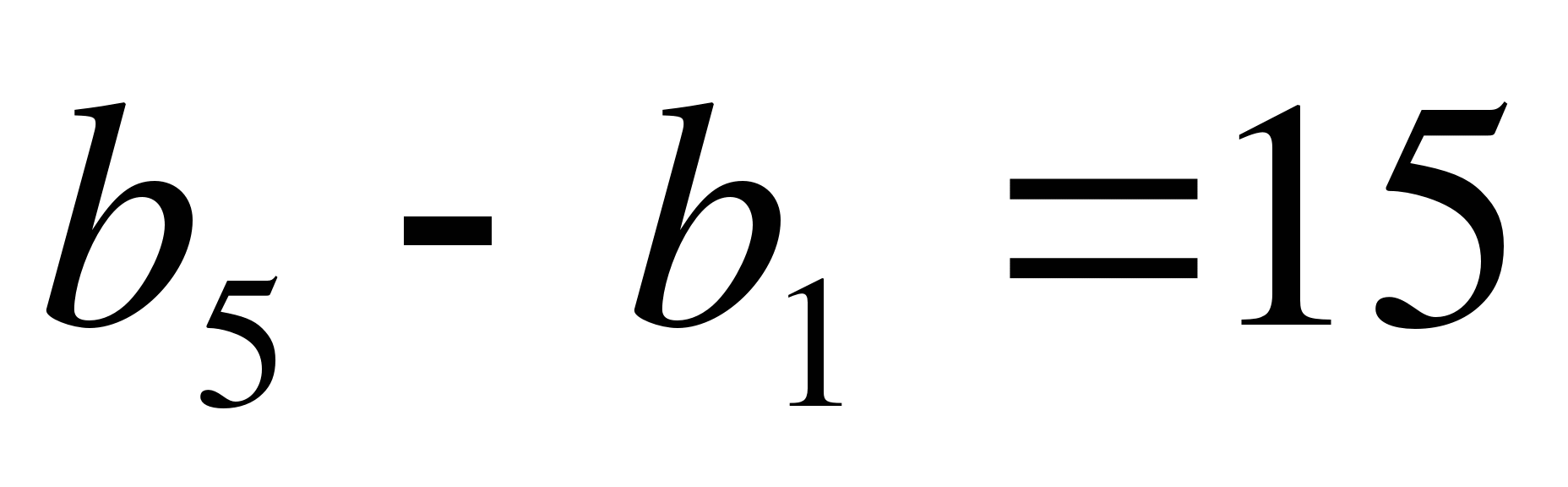 равна
равна
А) 31 или 11 Б) ![]() или
или ![]() В) 32 или 16
В) 32 или 16
-
Дана последовательность чисел -20,5;-19;-17,5;…, которая является геометрической прогрессией.
-
Формула его общего члена имеет вид:
-
А) ![]() Б)
Б) ![]() В)
В) ![]() Г) верного ответа нет
Г) верного ответа нет
1.2 Рекуррентное соотношение для этой прогрессии имеет вид
А) ![]() ;
; ![]() ; Б)
; Б)
![]() ;
; ![]()
В) ![]() ;
; ![]() Г)
верного ответа нет
Г)
верного ответа нет
1.3 Количество отрицательных чисел, которое содержит эта последовательность, равно
А) 15 Б) 12 В) 14 Г) верного ответа нет
1.4 Сумма n первых членов станет положительной, начиная
А) с 25 номера Б) с 28 номера В) с 29 номера Г) верного ответа нет
1.5 Значение выражения ![]() , где
, где
![]() ,
, ![]() ,
,
![]() ,…,
,…,![]() - члены этой
последовательности, равно:
- члены этой
последовательности, равно:
А) ![]() Б)
Б) ![]() В)
В) ![]() Г) верного ответа нет
Г) верного ответа нет
-
Укажите пять первых членов последовательности, заданной формулой ее - n-го члена
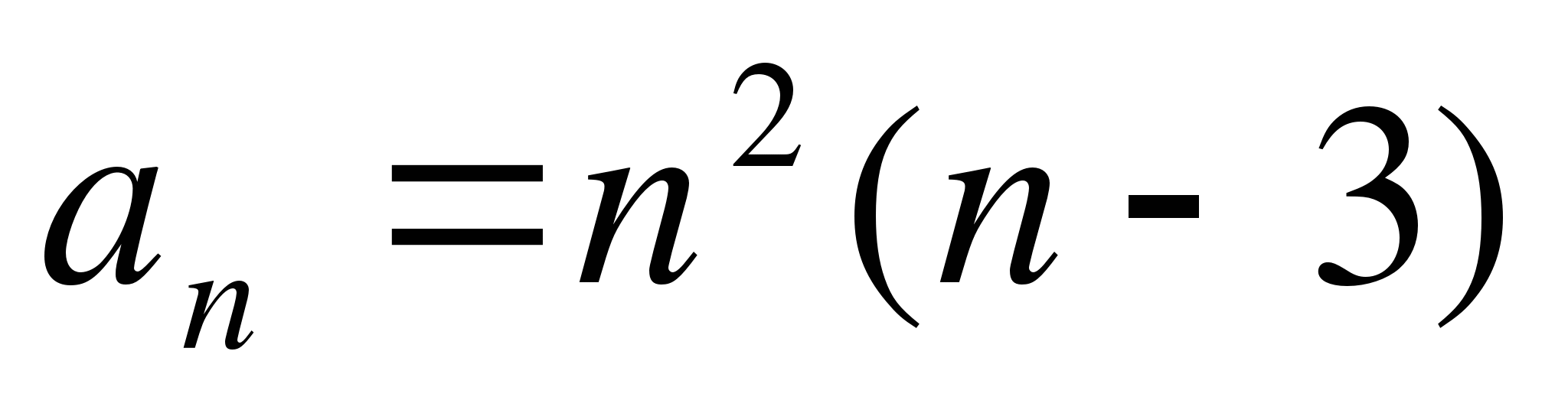
А) -2,-4,0,16,50 Б) 1,2,3,4,5 В) 0,-2,-4,-16,-50 Г) -4,-2,0,16,50
-
Четвертый член арифметической прогрессии 13,9,… равен:
А) 1 Б) 6 В) -1 Г) 0
-
В геометрической прогрессии
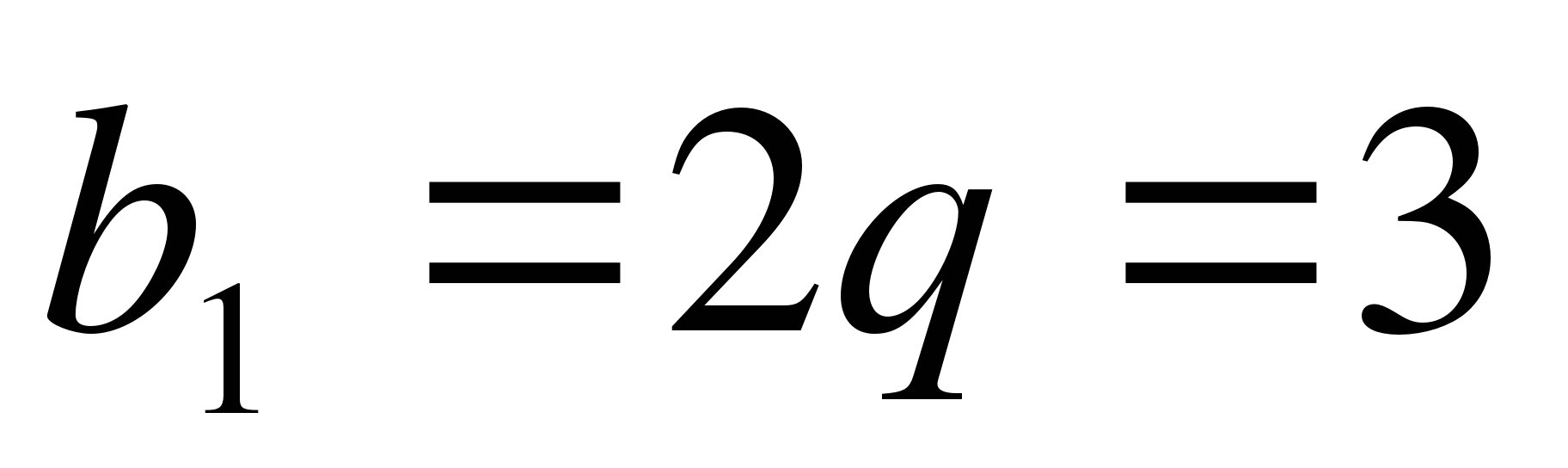 .
Найдите
.
Найдите 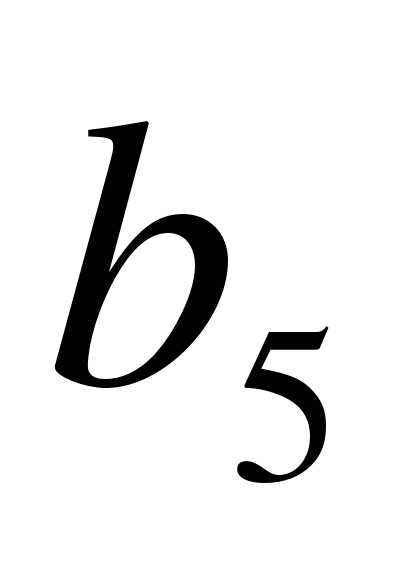 .
.
А) 162 Б) 180 В) 324 Г) 81
-
Число -22 является членом арифметической прогрессии 44,38,32,…. Найдите его номер.
А) 13 Б) 12 В) 11 Г) 10
-
В арифметической прогрессии сумма пятнадцати первых членов равна 0, а произведение 3 и 7 членов равна 20. С какого номера все члены данной прогрессии будет больше пятнадцати?
А) 64 Б) 16 В) 25 Г) 10 Д) 63 Е) 7 Ж) 88
-
В арифметической прогрессии сумма четырех первых членов равна 56, а сумма четырех последних членов равна 112. Найдите число членов прогрессии, если ее первый член равен 11.
А) 44 Б) 11 В) 15 Г) 10 Д) 55 Е) 201 Ж) 16
-
В арифметической прогрессии сумма третьего и пятого членов равна -14, а сумма первых девяти членов равна -45. Сколько отрицательных членов имеет эта прогрессия?
А) 220 Б) 7 В) 17 Г) 720 Д) 8 Е)608 Ж) 18
Приложение №6
Тесты на соответствие
-
Для каждой арифметической прогрессии, заданной формулой n-го члена, укажите ее разность d.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) d = 7 2) d = -2 3) d = 2 4) d = 5
-
Для каждой арифметической прогрессии, заданной
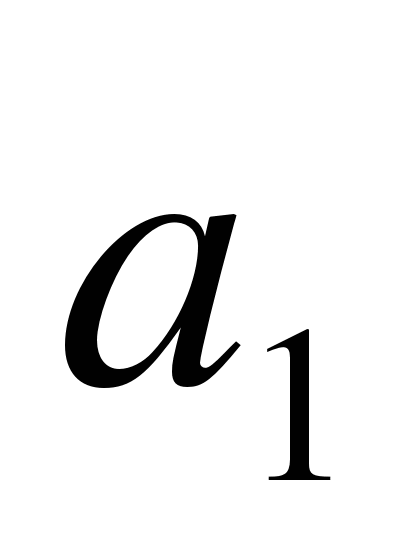 и d, укажите формулу ее
n-го члена.
и d, укажите формулу ее
n-го члена.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Для каждой арифметической прогрессии, заданной
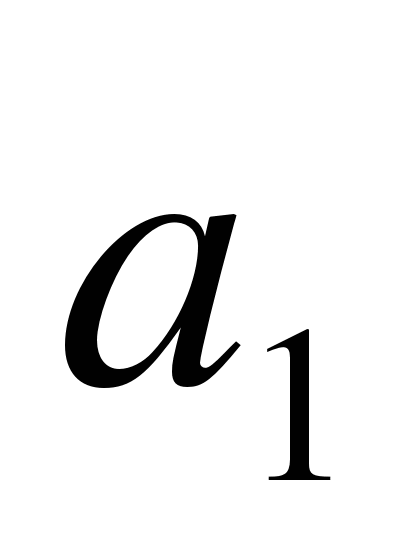 и d, укажите формулу ее
n-го члена.
и d, укажите формулу ее
n-го члена.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Для каждой арифметической прогрессии, заданной формулой n-го члена, укажите ее разность d.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) d = 3 2) d = -4 3) d = 4 4) d = 4
-
Для каждой арифметической прогрессии, заданной формулой n-го члена, укажите ее разность d.
А) ![]() Б)
Б) ![]() В)
В) ![]()
![]()
1) d = 5 2) d = 7 3) d = -7 4) d = 3
-
Для каждой арифметической прогрессии, заданной формулой n-го члена, укажите ее разность d.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) d = -2 2) d = 5 3) d = 2 4) d = 3
-
Для каждой арифметической прогрессии, заданной
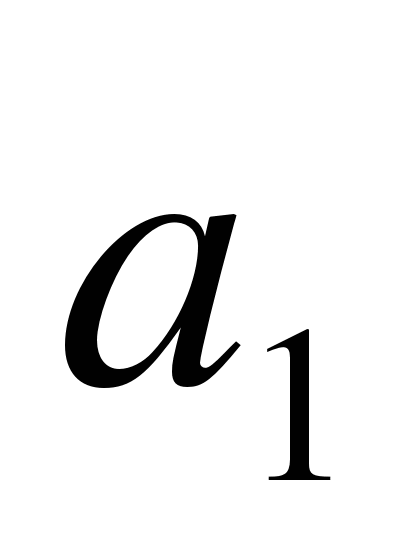 и d, укажите формулу ее
n-го члена.
и d, укажите формулу ее
n-го члена.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Для каждой арифметической прогрессии, заданной формулой n-го члена, укажите ее разность d.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) d = 3 2) d = -4 3) d = 4 4) d = 7
-
Для каждой арифметической прогрессии, заданной формулой n-го члена, укажите ее разность d.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) d = -2 2) d = 5 3) d = 2 4) d = 3
-
Для каждой арифметической прогрессии, заданной формулой n-го члена, укажите ее разность d.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) d = -5 2) d = 4 3) d = 7 4) d = 5
-
Для каждой арифметической прогрессии, заданной
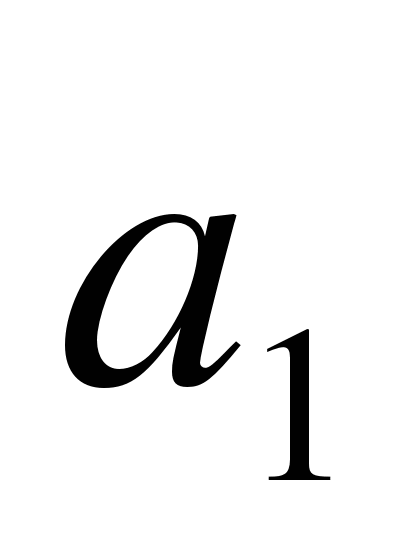 и d, укажите формулу ее
n-го члена.
и d, укажите формулу ее
n-го члена.
А) ![]() Б)
Б) ![]() В)
В) ![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
-
Каждой последовательности, заданной формулой n-го члена (левый столбец), поставьте в соответствии верное утверждение (правый столбец)
А) ![]() 1) Последовательность -
арифметическая прогрессия
1) Последовательность -
арифметическая прогрессия
Б) ![]() 2) Последовательность -
геометрическая прогрессия
2) Последовательность -
геометрическая прогрессия
В) ![]() 3) Последовательность не
является прогрессией
3) Последовательность не
является прогрессией
13)Известно, что (![]() ) -
арифметическая прогрессия
) -
арифметическая прогрессия ![]() ,
, ![]() . Найдите: 1)
. Найдите: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
А) 14 б) 22 В) 26 Г) 18
Приложение № 7
Тренировочные задания по теме:
«Арифметическая прогрессия» 9 класс
1 работа:
1 вариант
-
В арифметической прогрессии найти а20, если а1=3, d=4.
А) 75 Б) -75 В) 79 Г) -79
-
Дана арифметическая прогрессия 8,2;6,6;… Найдите номер члена этой прогрессии, равного -15,8.
А) 16 Б) 14 В) 17 Г) Нет такого номера
-
Найдите сумму первых шестнадцати членов арифметической прогрессии, заданной формулой аn=6n+2.
А) 864 Б) 848 В) 792 Г) 716
-
Сколько членов арифметической прогрессии -2; 2… меньше числа 55?
А) 15 Б) 19 В) 16 Г) 13
-
Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условия a90>0.
А) an=-4n+500 Б) an=-4n В) an=4n-400 Г) an=4n-360
2 вариант
-
В арифметической прогрессии найти а15, если а1=2, d=3.
-
Дана арифметическая прогрессия -3,5;-2;… Найдите номер члена этой прогрессии, равного 59,5.
-
Найдите сумму первых четырнадцати членов арифметической прогрессии, заданной формулой аn=5n-1.
-
Сколько членов арифметической прогрессии -12,-8,… меньше числа 48?
-
Найдите первый член арифметической прогрессии, если а2= -7, а7=18.
2 работа:
1 вариант
-
Запишите формулу n-го члена числовой последовательности чисел кратных 5.
-
n-5 2)

 3) n + 5 4) 5n
3) n + 5 4) 5n
-
Из данных арифметических прогрессий (сn) выберите ту, среди членов
которой есть число 4,5.
-
cn= 2n+3 2) cn=2n+1 3) cn=3,5+n 4) cn=3,5n-1
-
В арифметической прогрессии (аn) известно: а1=7, d= -0,5. Найти a7.
-
4,5 2) -1 3) 4 4) 3,5
-
Каким будет десятый член арифметической прогрессии 1; 3; 5; 7;…?
-
21 2) 20 3) 19 4) 23
-
Соотнести формулу n-ого члена и значения разности арифметической прогрессии.
А) an=5n+7 Б) bn=2n+5 В)cn=7n-2
1) d=7 2) d=3 3) d=2 4) d=5
-
2 вариант
1. Запишите формулу n-го члена числовой последовательности чисел кратных 3.
2. В арифметической прогрессии (аn) известно: a1=0,4, d= -0,2. Найти a4.
3. Найдите разность арифметической прогрессии, если известно, что пятый ее член равен 29, а девятый член равен 45.
4. Каким будет следующий член арифметической прогрессии 14; 2;
-
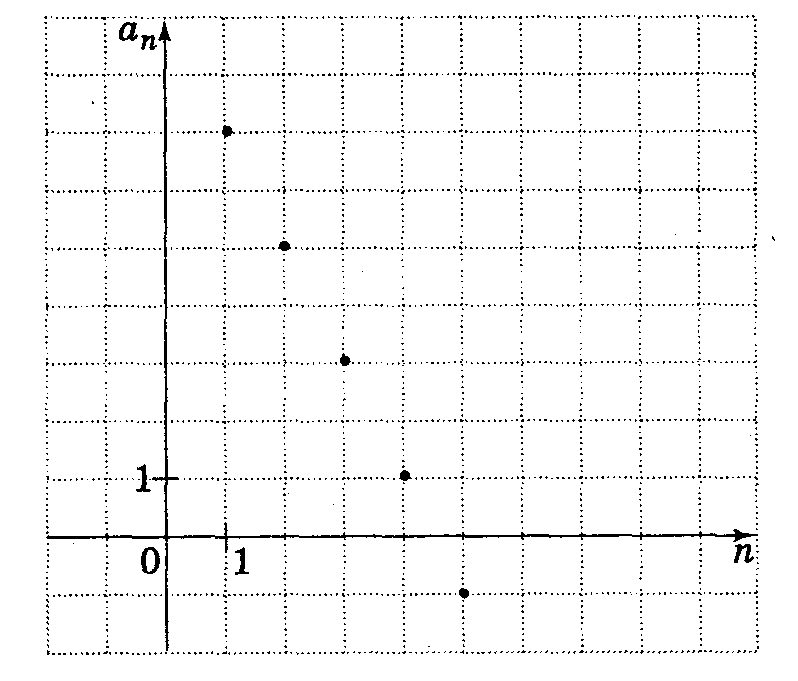 10;…?
10;…?
5. Используя данные рисунка найти a17.
3 работа:
1 вариант
-
Найдите такое число х, что числа: 2, х2, 6 образуют арифметическую прогрессию.
А) 3 Б) 4 В) 2 Г) -2
-
Дана арифметическая прогрессия: -2,8; -2,5; …. Укажите наименьший по абсолютной величине член арифметической прогрессии.
А) 0,1 Б) -0,1 В) 0,2 Г) -0,3
-
Вычислите сумму 30+31+32+…+38+39+40.
А) 322 Б) 385 В) 324 Г) 325
-
Ракета за первую секунду пролетела 300 м. За каждую секунду ракета пролетала на 200 м больше, чем за предыдущую. Какое расстояние (в километрах) пролетела ракета за шестую секунду?
А)1,3 Б) 1,2 В) 1,4 Г) 1,1
5. В арифметической прогрессии (аn) а5=10, а10=25. Найдите сумму первых 20 членов этой прогрессии.
А) 520 Б) 580 В) 530 Г) 630
2 вариант
-
Составьте формулу для вычисления суммы всех натуральных чисел от 4 до n включительно.
-
Числовая последовательность задана формулой n-го члена an=
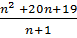 . Найдите номер члена
последовательности равного 26.
. Найдите номер члена
последовательности равного 26.
-
Катя поступила на работу официанткой в кафе. В первый месяц ее зарплата составляла 3500 р. В каждый следующий месяц зарплата повышалась на 200р. Сколько Катя заработала за год?
-
Между числами 3 и 48 вставьте такие три числа, которые вместе с данными числами образуют арифметическую прогрессию. В ответе запишите найденные три числа.
-
Найдите сумму членов арифметической прогрессии, кратных 3 и не превосходящих 110.
«Арифметическая прогрессия»
</ ответы
1 работа
1)а20=79 (в)1)а15=44
2)n=16 (а)
2)n=43
3)S16=848 (б)
3)S14=511
4)n=15 (а)
4)n=15
5)а90>0 (а)
5)а1=12
2 работа
1)аn=5n (4)1)аn=3n
2)аn=3,5+n (3)
2)а4=-0,2
3)а7=4 (3)
3)d=4
4)а10=19 (3)
4)а4=-22
5)А-4; Б-3; В-1
5)а17=-25
3 работа
1)2 (в); -2 (г)1) Sn
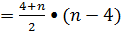
2)а10=-0,1 (б)
2)n=7
3)385 (б)
3)55 200
4)1,3 (а)
4)а2=14,25; а3=25,5; а4=36,75
5)530 (в)
5)Sn=1998
Приложение №8
Тренировочные задания по теме:
«Геометрическая прогрессия» 9 класс
1 работа:
1 вариант
1. Найдите знаменатель геометрической прогрессии 4; 2; 1
2. Найдите номер члена геометрической прогрессии равного 192.
6; 12; 24;…; 192;…;
3. Выпишите три первые члена геометрической прогрессии, если b1=2, q=3.
4. Найдите четвертый член геометрической прогрессии -4; -16;…;
5. Найдите знаменатель геометрической прогрессии, если b1=2, b5=162
2 вариант
-
Найдите знаменатель геометрической прогрессии -10; 20; -40.
-
4 2) -2 3)
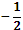 4) 2
4) 2
-
Найдите номер члена геометрической прогрессии равного 324.
4; 12; 36;…;324;…;
-
5 2) 7 3) 13 4) 10
-
Найдите знаменатель геометрической прогрессии, если b1= -128; b7= -2 1)
 2) 3 3)
2) 3 3)
 4)
4)

4. Выпишите три первые члена геометрической прогрессии, если b1=3; q=2.
-
-
3; 9; 27 2) 3; 6; 12 3) 12; 6; 3 4) 3;
 ;
;

-
5. Найдите четвертый член геометрической прогрессии 2; -6; …;
-
54 2) 48 3) -54 4) 112
2 работа:
1 вариант
1. Дана геометрическая прогрессия 2, 6, 18,… Найдите восьмой член этой прогрессии.
2. Найдите седьмой член и знаменатель геометрической прогрессии с положительными членами, если: b8=
 ,,
b6= 81.
,,
b6= 81.
3. Найтиb5и b1 геометрической прогрессии, если b4=5, b6=20
4. Геометрическая прогрессия задана формулой n-го члена: bn=3 •
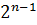 .
Найти S5.
.
Найти S5.
-
В геометрической прогрессии найти b5и S4, если b2=15, b3=25, q
 0.
0.
2 вариант
1. Дана геометрическая прогрессия 2, 6, 18,… Найдите номер члена последовательности, равного 162.
1)9 2) 3 3) 5 4) 8
-
-
Найдите седьмой член и знаменатель геометрической прогрессии с положительными членами, если: b6=9; b8=3.
-
-
b7=3 2) b7=
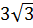 3)
b7=
3)
b7=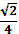 4) b7=
4) b7=
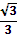
q=
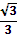 q=
q=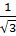 q=2 q=3
q=2 q=3
-
-
Найти b1и b5 геометрической прогрессии, если b4=9, b6=4.
-
1) b5=6 или b5= -6; b1= 30
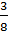 или b1=
или b1=
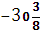
2) b5=3 или b5= -3; b1
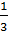 =
3
=
3 или b1=
-3
или b1=
-3
3)b5=
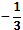 или b5=
или b5= ; b1=
; b1=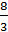 или b1=
или b1=
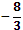
4) b5=
 или b5=
или b5= 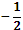 ; b1=4 или
b1= - 4
; b1=4 или
b1= - 4
4. Геометрическая прогрессия задана формулой n-го члена: bn=
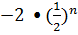 , найти
S6.
, найти
S6.
-
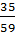 2)
2
2)
2 3)
-1
3)
-1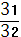 4) -3
4) -3
-
В геометрической прогрессии найти b5и S4, если b2=14, b4=686, q>0.
-
b5=4325, S4=3000 2) b5=4802, S4=800 3) b5=8000, S4=4802
-
4) b5=2300, S4=1005
3 работа:
1 вариант
1. Между числами 2 и -18
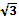 , вставьте четыре числа так,
чтобы получилась геометрическая прогрессия. В ответ запишите
эти числа.
, вставьте четыре числа так,
чтобы получилась геометрическая прогрессия. В ответ запишите
эти числа.
2. Сумма первых четырех членов геометрической прогрессии равна - 40, знаменатель прогрессии равен -3. Найдите сумму первых восьми членов прогрессии.
3. Сумма третьего и четвертого члена геометрической прогрессии равна 16, а сумма четвертого и пятого членов равна -32. Найти знаменатель прогрессии.
2 вариант
1. Между числами 3 и -12
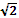 , вставьте четыре числа так,
чтобы получилась геометрическая прогрессия.
, вставьте четыре числа так,
чтобы получилась геометрическая прогрессия.
1)
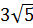 ; 4;
; 4;
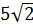 ; 8 2)
; 8 2) 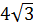 ;
; 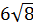 ;
; 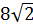 ;
; 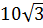
3)-3
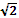 ;
6; -6
;
6; -6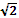 ;
12 4)
;
12 4)
 ;
; 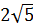 ;
;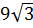 ; 11
; 11
-
-
Сумма первых трех членов геометрической прогрессии равна 39, знаменатель прогрессии равен -4. Найдите сумму первых шести членов прогрессии.
-
-
1226 2) -2457 3) 5657 4) 2457
-
-
Сумма первого и второго члена геометрической прогрессии равна 108, а сумма второго и третьего членов равна 135. Найти первые три члена этой прогрессии.
-
1) 3 ;

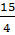 ;
;  2) 60; 48; 38,4 3) 48; 60;
75 4) 75; 60; 48
2) 60; 48; 38,4 3) 48; 60;
75 4) 75; 60; 48
«Геометрическая прогрессия»
ответы
1 работа
1)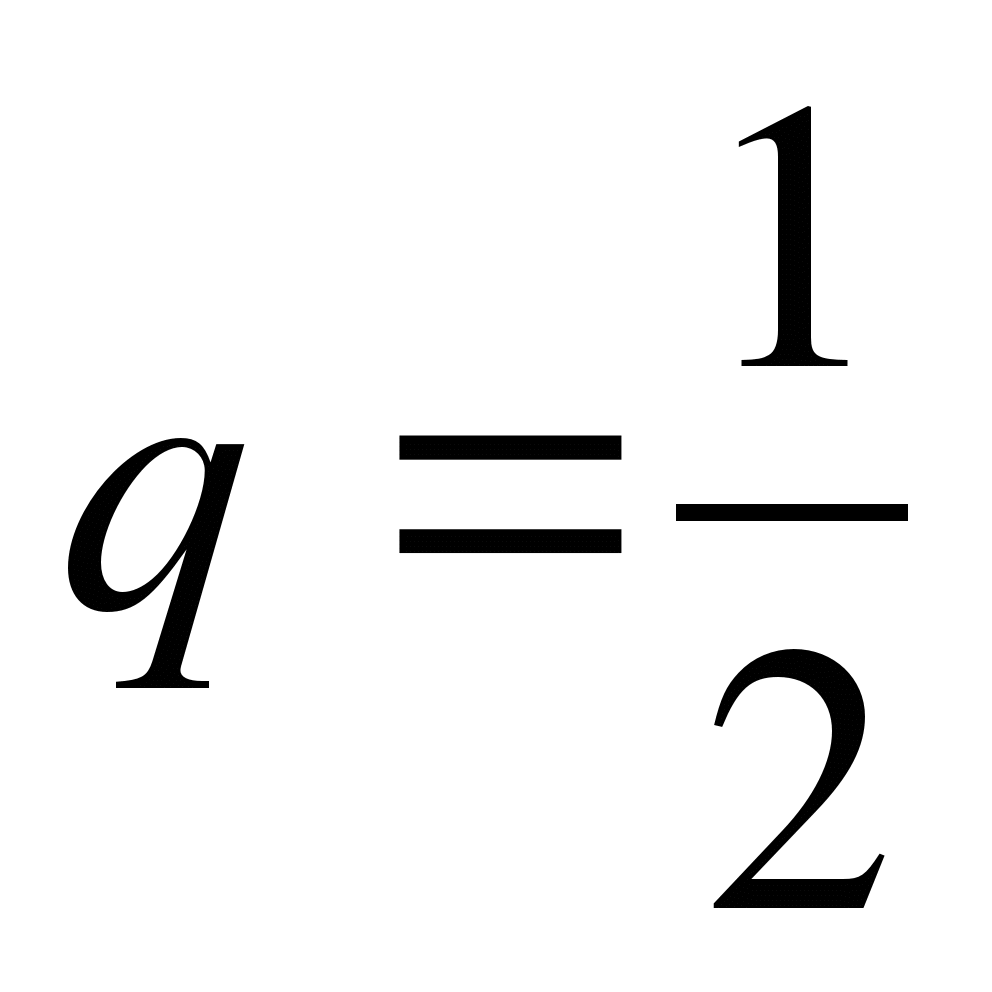
1)q=-2 (2)
2)n=6
2)n=5 (1)
3)b1=2; b2=6; b3=18
3)
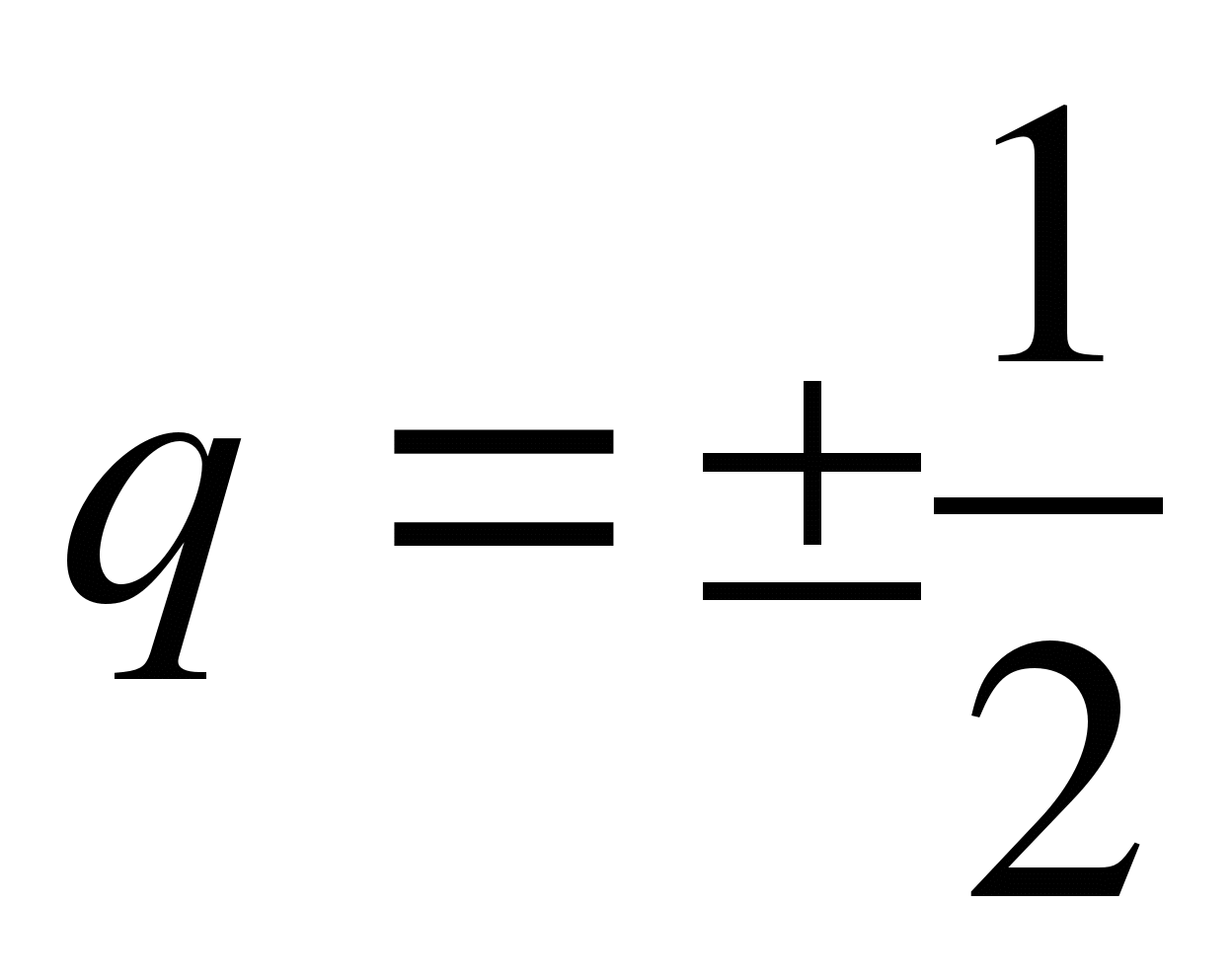
4)b4=-256
4) 3; 6; 12 (2)
5)
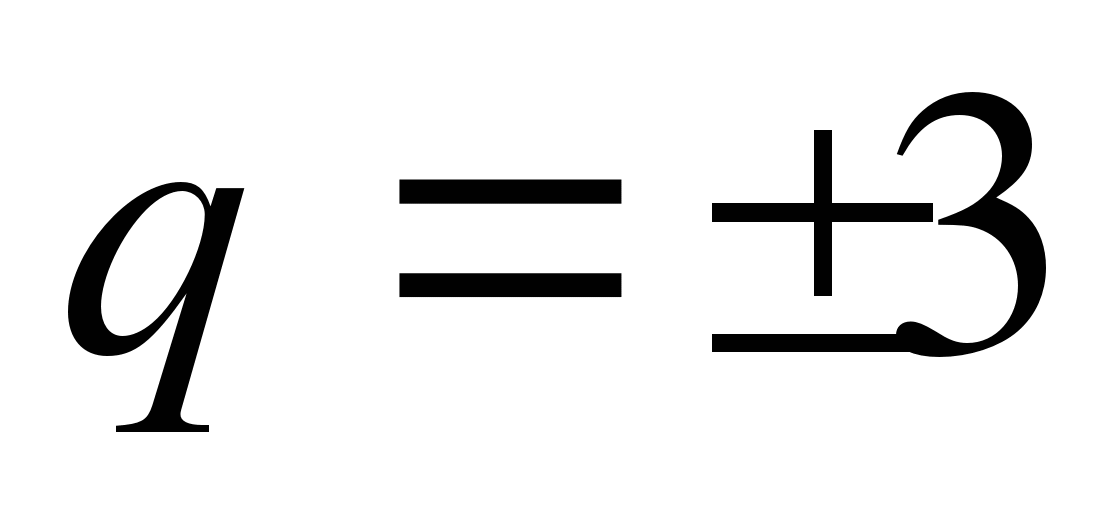
5) ) b4=48 (2)
2 работа
1)b8=43741)n=5 (3)
2)b7=3
2)q=
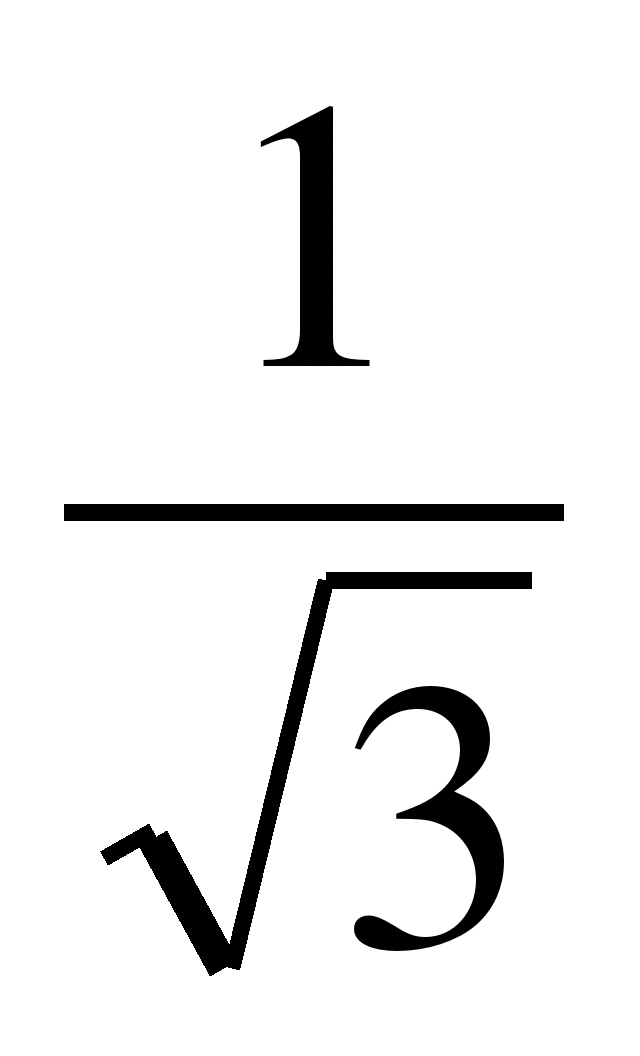 ;
b2=
;
b2=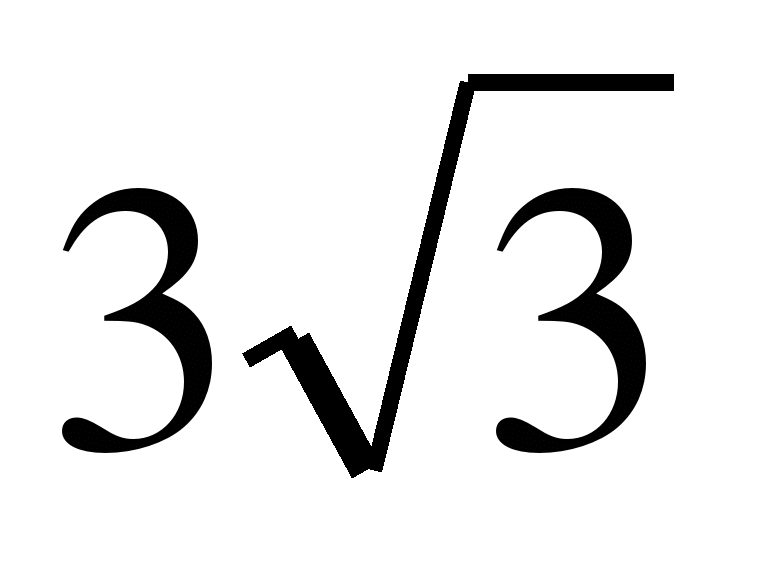 (2)
(2)
3)b5=10; b1=
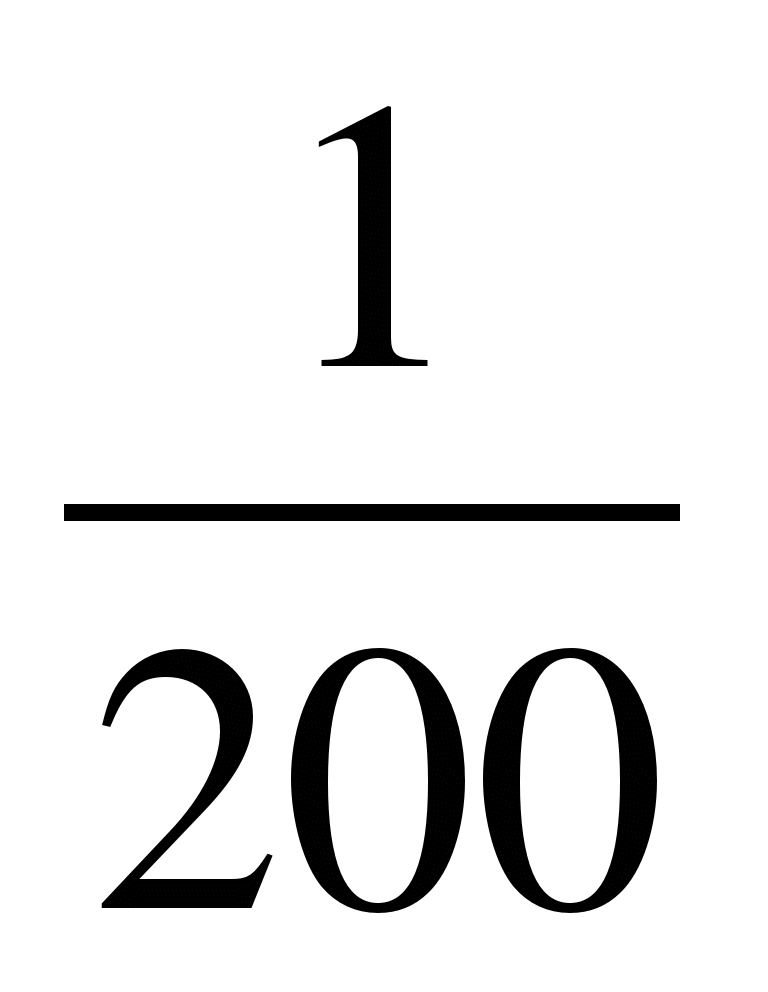
3)b5=
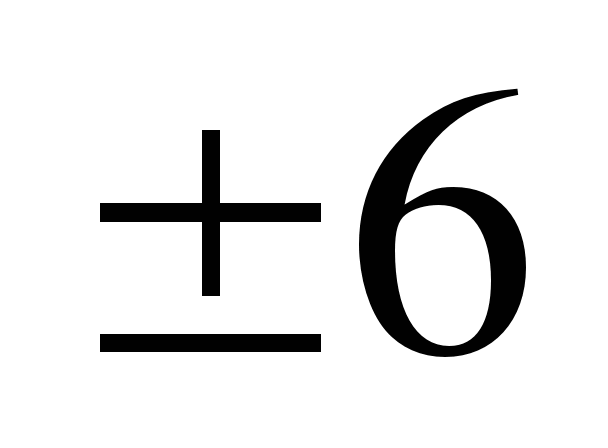 ;
b1=
;
b1=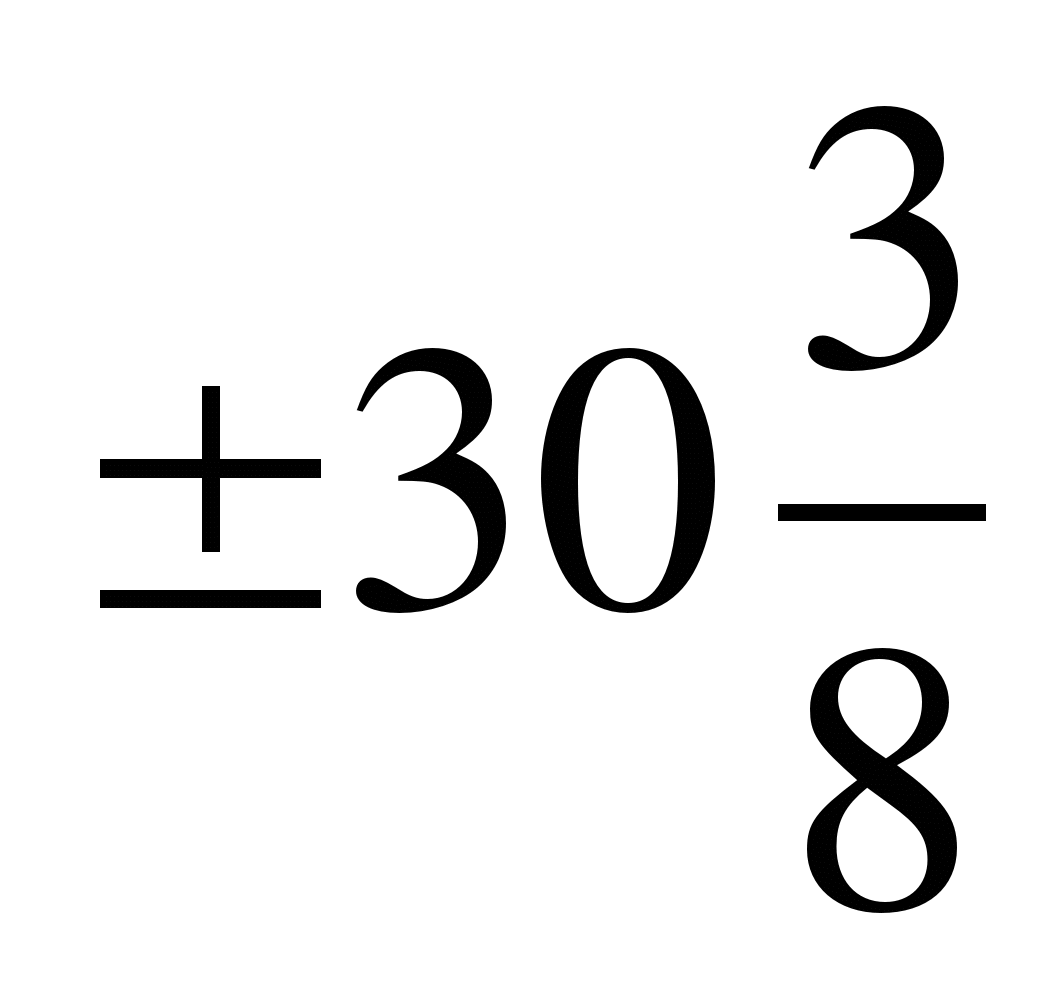 ()
()
4)S5=93
4)S6=-
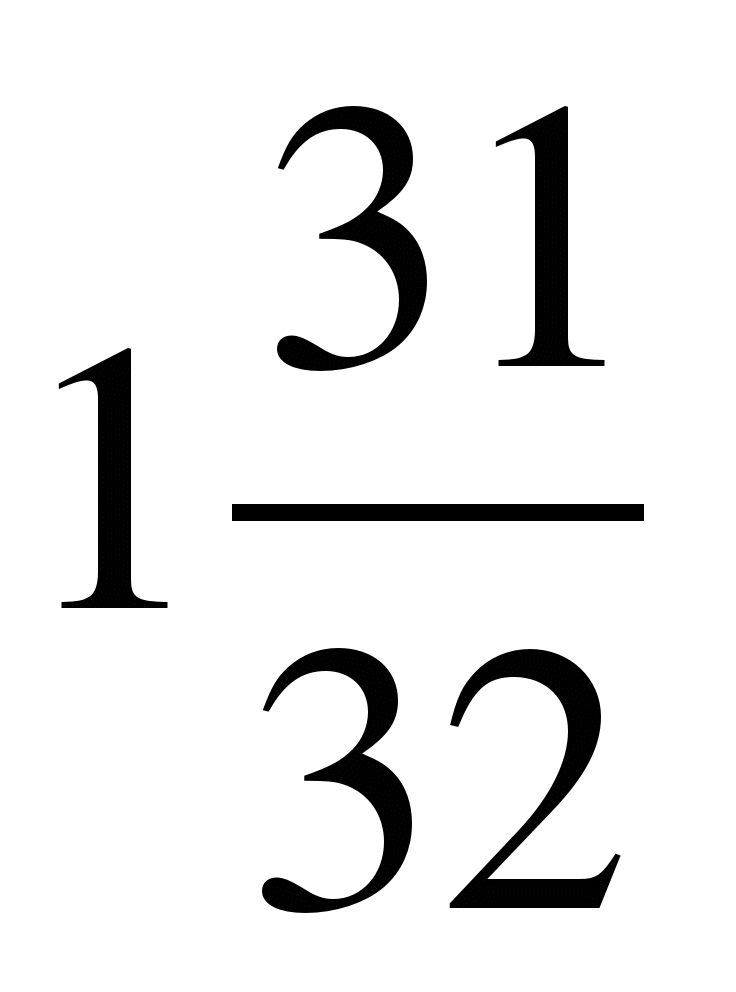 (3)
(3)
5)b5=
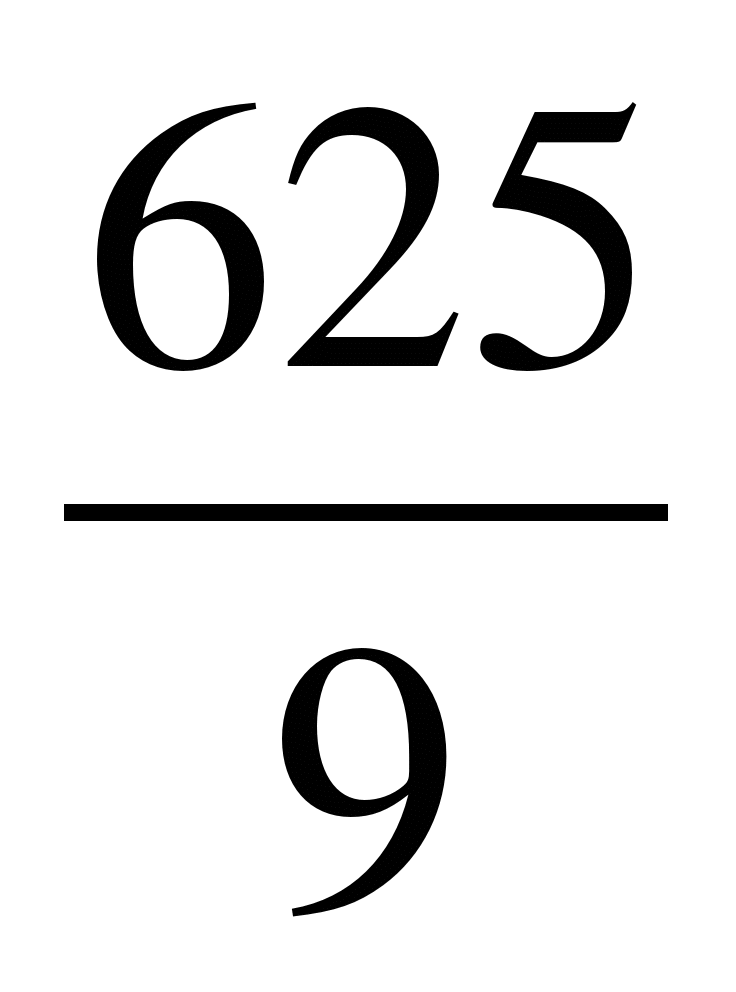 ;
S4=-
;
S4=-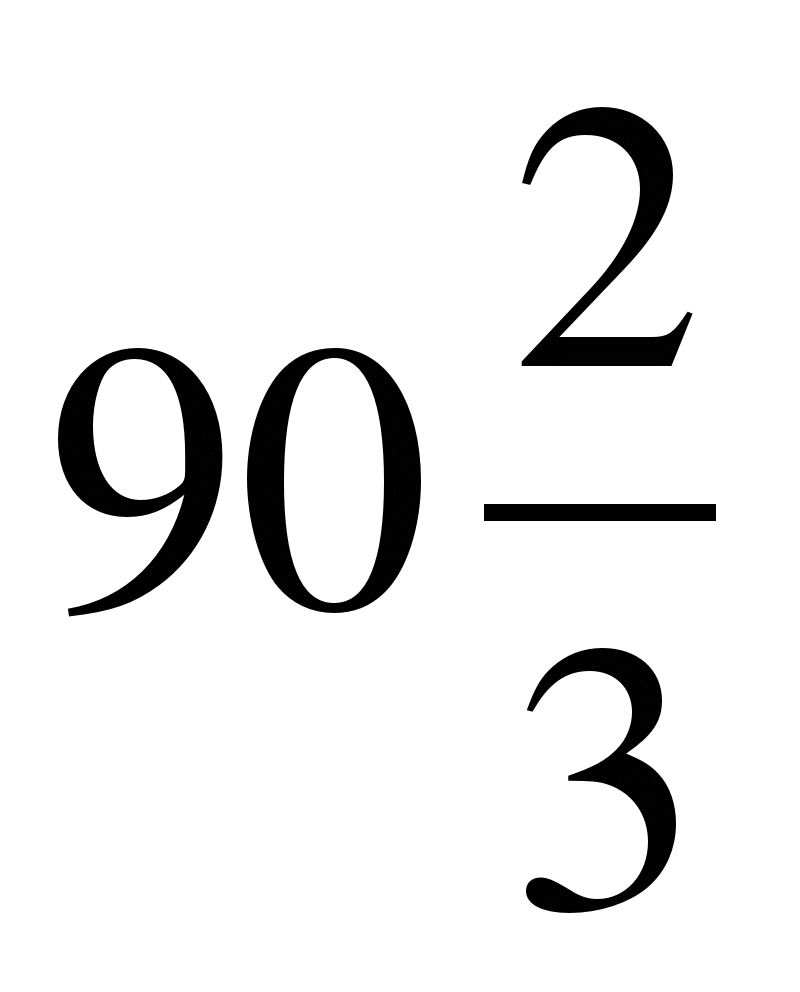
5)b5=4802; S4=800()
3 работа
1)b2=-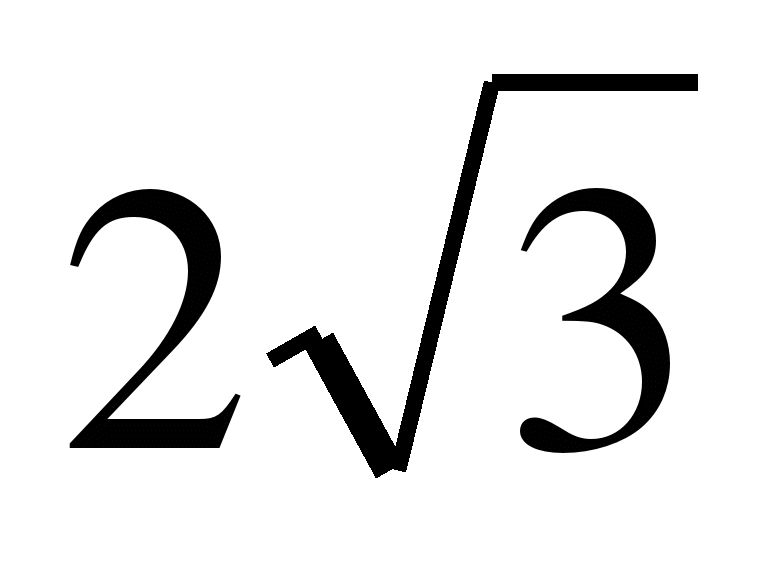 ;
b3=6; b4=-
;
b3=6; b4=-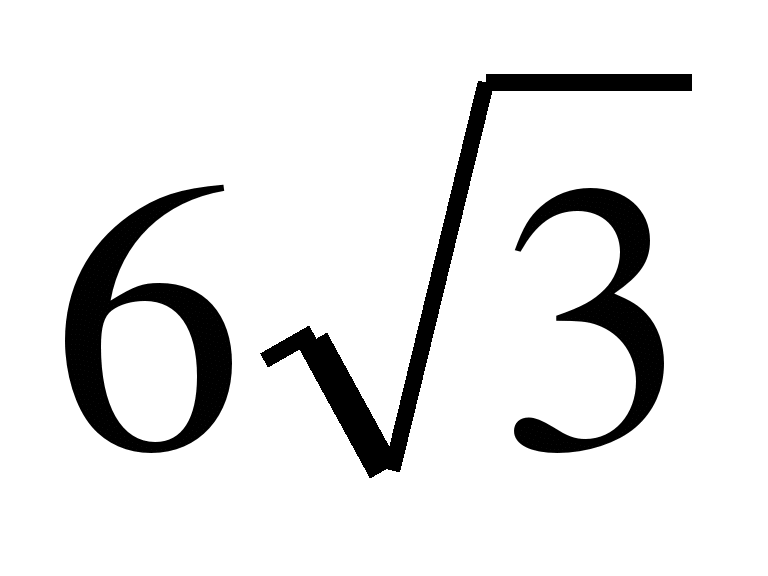 ;
b5=18
;
b5=18
1) -
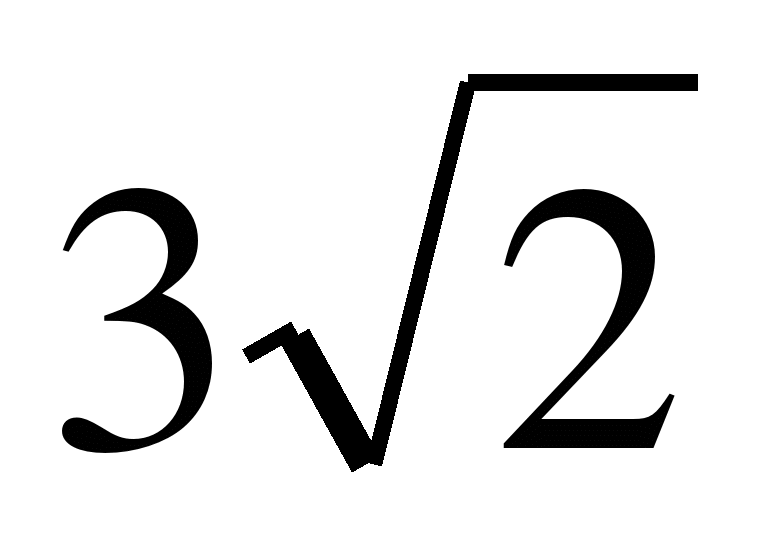 ; 6: -
; 6: -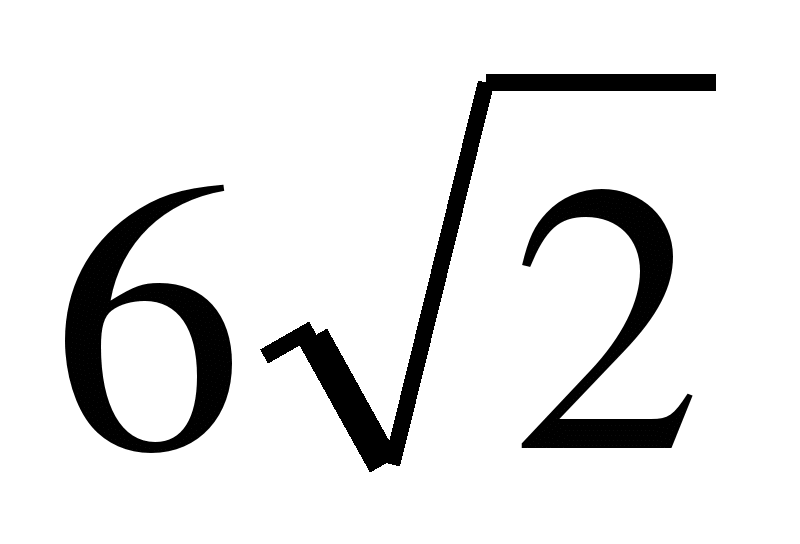 (3)
(3)
2)S8=6561
2)-2457 (2)
3)q=-2
3)48; 60; 75 (3)
-