Проектная работа по математике 'Функционально-графические методы при решениии уравнений' (11 класс)

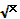
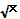
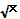
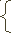
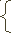
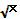
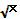
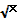
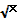
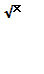
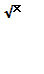
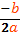
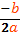
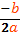
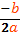
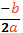
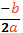
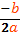
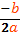
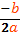
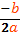
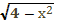
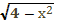
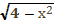
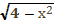
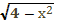
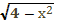
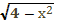
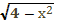
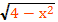
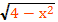
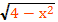
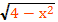
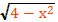
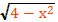
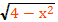
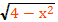
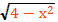
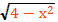
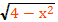
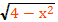
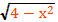
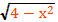
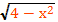
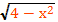
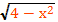
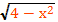
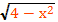
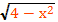
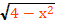
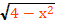
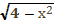
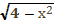
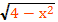
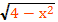
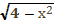
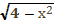
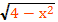
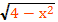
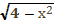
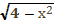
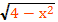
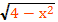
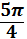
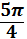
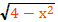
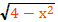
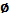
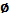
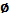
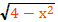
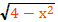
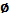
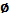
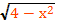
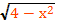
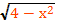
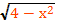
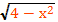
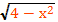
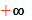
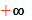
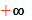
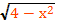
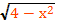
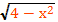
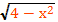
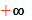
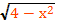
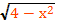
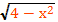
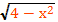
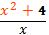
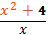
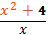
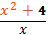
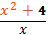
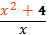
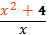
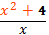
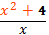
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

XXVI НАУЧНО - ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ УЧАЩИХСЯ

СЕКЦИЯ «МАТЕМАТИКА»

Функционально - графические методы при решении уравнений.

Выполнила : Шведова Мария, учащаяся 11 информационно-математического класса МОУ Богучарский лицей

Руководитель: Кобелева Татьяна Васильевна учитель математики ВКК

МОУ Богучарский лицей

ВОРОНЕЖ 2011 ГОД.

Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определённых умственных навыках, которые проявляются в обобщении, конкретизации, анализе, синтезе. Для реализации этих задач математического образования большую роль играют нестандартные задачи, при решении которых развивается творческое и логическое мышление, формируются способности нестандартно мыслить, проявляется самостоятельность, умение применять способы решения задачи в практической деятельности, использовать полученные знания и умения в решении прикладных и практических задач.

Тема моей работы «Функционально-графические методы при решении уравнений», в которой, как мне кажется, мне удалось показать рациональность применения этих методов по сравнению с другими. Альберт Эйнштейн говорил так: «Мне приходится делить время между политикой и уравнениями. Однако политика существует только для данного момента, а уравнения будут существовать вечно». Вот и сейчас в центре нашего внимания будут уравнения.

Для работы с уравнениями обычно используют функционально - графические методы. Они основаны на:

• использовании монотонности и четности функции;

• использовании ограниченности функции;

• графическом методе

• нахождении области определения и области значения функции.

Обычно функционально- графические методы применяют, когда в обеих частях уравнения стоят функции разного вида, когда в одной части уравнения стоит функция, ограниченная сверху или снизу, а в другой - конкретное число и когда в одной части уравнения функция, ограниченная сверху, а в другой - ограниченная снизу.

Порядок решения уравнения функциональным методом:

• определение свойств функции

• нахождение ОДЗ или промежутков монотонности функции (в зависимости от свойства функции).

• нахождение корня подбором, решение системы уравнений.

Функциональный метод, как правило, используется для уравнений, содержащих разные функции. Но не всякое уравнение вида f(x)=g(x) в результате преобразований может быть приведено к уравнению того или иного стандартного вида, для которого подходят обычные методы решения. В таких случаях имеет смысл использовать такие свойства функций f(x) и g(x) как монотонность, ограниченность, четность, периодичность и др.

Четность функции.

Пример1.

Может ли уравнение 2х⁸+3ах⁶+4х⁴-ах²=5 при каком-либо а 5 корней?

Решение.

F(x) - четная ( D (y): R - функция 2х⁸+3ах⁶+4х⁴-ах²=5 симметрична относительно 0,

F(x) =F (-x)), значит если х₀ - корень уравнения, то и (- х₀) тоже корень уравнения.

х₀=0 не является корнем уравнения, т.к. 2*0⁸+3а*0⁶+4*0⁴-а*0²≠0. Значит, уравнение может иметь только четное количество корней. Следовательно, 5 корней уравнение иметь не может.

Ответ: Уравнение не может иметь 5 корней.

Пример2.

Найти все значения a и b, при которых имеет только одно решение (х;у), х>0, система

=а

х²+у²=b.

Решение.

Если пара (х₀;у₀) удовлетворяет этой системе, то и пара (х₀;-у₀) также ей удовлетворяет. Для второго уравнения это очевидно, для первого следует из равенства

= = .

Значит, если система имеет единственное решение, то у₀=0 и а=0.

При этом получим систему:

х^у=1

х²+у²=b

Ясно, что b>0. Из первого уравнения имеем или у=0 или х=1.

1. у=0 2) x=1 3) x=0

х⁰=1 1^y=1 0=1 - неверное равенство

х²+у²= b 1+у²= b 0²+у²= b

1=1 1=1

х²= b у²= b-1

1=1 1=1

х= y=±

Если b>1, то имеем еще 2 решения: х=1, y=±.

Если b<0, то больше решений нет.

Если b=1, то получаем туже пару чисел х=1, у=0.

Ответ: а=0, 0<b≤1.

Теоремы, связанные с монотонностью функций.

Теорема №1.

Если в уравнении f(x)=g(x) f(x) - убывающая, а g(x) - возрастающая, то уравнение имеет не более одного корня.

Рассмотрим примеры, при решении которых можно применить данную теорему.

Пример 1.

Решить уравнение 2^X = 3 - x

2^X = 3 - x

x= 1 является корнем уравнения, т.к. 2¹=3 - 1

2 = 2 - верное равенство

А т.к. у = 2^{X -} возрастающая, а у = 3 - х - убывающая, то уравнение корней более не имеет.

Ответ: х=1

Пример 2.

Решить уравнение log_1/3 x= x - 4

log_1/3 x= x - 4

x = 3 - является корнем уравнения, т.к. log_1/3 3 = 3 - 4

-1 = - 1 - верное равенство

А т.к. у = log_1/3 x - убывающая, а у = х - 4 - возрастающая, то уравнение корней более не имеет.

Ответ: х = 3

Пример3.

Решить уравнение х²+1 = 2^-Х²

^{Решение.}

1. Решим данный пример с помощью теоремы.

х²+1 = 2^-Х²

х=0 является корнем уравнения, т.к. 0+1=2⁰

1=1 - верное равенство

А т.к. у= х²+1- возрастающая, а у=2^-Х² - убывающая, то уравнение больше не имеет корней.

Ответ: х=0.

2. Решим данный пример графическим способом.

х²+1 = 1/2^Х²

Построим графики уравнений у= х²+1 и у=1/2^Х² .

х

-2

-1

0

1

2

у

5

2

1

2

5

, у= х²+1

х

-2

-1

0

1

2

у

1/16

1/2

1

1/2

1/16

, у= 1/2^Х²

у= х²+1

УГрафическим решением данного уравнения будет являться абсцисса точки пересечения этих графиков. Очевидно, что это 0.

у= 1/2^Х²Графики данных функций не очень сложно построить, но в данном случае решение графическим способом займет гораздо больше времени, чем решение этого, же уравнения с помощью теоремы.

Х

Теорема №2.

Если в уравнении f(x) = c f(x) - монотонна, а с = const, то уравнение имеет не более одного корня.

Обратимся к примерам, при решении которых можно применить данную теорему.

Пример 1.

Решить уравнение 2^X + 5^X = 7^X

Решение.

2^X + 5^X = 7^X │: 7^X ≠ 0

(2/7)^X + (5/7)^X = 1

x=1 - является корнем уравнения , т.к. (2/7)¹ + (5/7)¹ = 1

1=1 - верное равенство

А т.к. у= (5/7)^X - убывающая и у=(2/7)^X - убывающая, следовательно y = (2/7)^X + (5/7)^X - убывающая и 1=const, то уравнение не имеет больше корней.

Ответ: х= 1

Пример 2.

Уравнение части С ЕГЭ - 2003 года.

Решить уравнение 2^x + 3^x + 4^x = 9^x

Решение.

2^x + 3^x + 4^x = 9^x

2^x + 3^x = 9^x - 4^x

2^x + 3^x = (2^x + 3^x)(2^x - 3^x )

(2^x + 3^x) - (2^x + 3^x)(2^x - 3^x) = 0

(2^x + 3^x )(1 - (2^x + 3^x)) = 0

2^x + 3^x = 0 или 1 - (2^x + 3^x)=0

Т.к. a^x > 0, то уравнение 1 - 2^x - 3^x =0

корней не имеет. 2^x + 1 = 3^x | : 3^x ≠0

(2/3)^x + (1/3)^x = 1

x = 1 является корнем уравнения.

А т.к. y = (2/3)^x - убывающая, у = (1/3)^x -

убывающая, следовательно

у = (2/3)^x + (1/3)^x -убывающая и 1 = const,

то уравнение не имеет больше корней.

Ответ: х = 1

Пример3.

Решить уравнение log₂x + 3log₂(x+3)=6

Решение.

log₂x + 3log₂(x+3)=6

Заметим, что y= log₂x - возрастающая, у= 3log₂(x+3) - возрастающая, следовательно у= log₂x + 3log₂(x+3) - возрастающая (т.к. сумма двух возрастающих функций есть функция возрастающая). Т.к у= log₂x + 3log₂(x+3) - возрастающая, а 6 =const, то уравнение имеет не менее одного корня.

х= 1 является корнем уравнения, т.к. log₂1 + 3log₂(1+3)=6

log₂1 + 3log₂4=6

0 + 3*2=6

6 = 6 - верное равенство.

Ответ: х=1.

Пример4.

Решить уравнение ()^Х+()^Х=()^Х

Решение.

()^Х+()^Х=()^Х |: ()^Х≠0

()^Х + ()^Х= 1

Т.к. у= ()^Х - убывающая, у= ()^Х - убывающая, следовательно

у=()^Х + ()^Х - убывающая (т.к. сумма убывающих функций есть функция убывающая), а т.к. у=()^Х + ()^Х - убывающая и 1=const, то уравнение имеет не более одного корня.

Очевидно, что х=2 является корнем уравнения, т.к. ()² + ()²= 1

+ = 1

= 1

= 1

1 = 1 -верное равенство

Ответ: х=2.

Пример5.

Уравнение части С ЕГЭ - 2009 года.

Решить уравнение + =

Решение.

Заметим, что у= + - возрастающая (т.к. сумма двух возрастающих функций - возрастающая), =const (т.к. а есть некоторое число). Следовательно, данное уравнение имеет не более одного корня.

Очевидно, что х =а является корнем уравнения, т.к. + =

+ =

= - верное равенство.

Ответ: х=а.

Пример6.

Решить уравнение + = 1.

Решение.

Т.к. у= - возрастающая, у= - возрастающая, а значит и

y= + - возрастающая (т.к. сумма возрастающих функций есть функция возрастающая) и 1=const, то уравнение имеет не более одного корня.

х=1/2 - является корнем уравнения, т.к.

+ = 1

+ = 1

+ = 1

+ = 1

= 1

1=1- верное равенство.

Ответ: х=1/2.

Нужно отметить, что решить аналитическим способом данное уравнение проблематично. Преобразуем уравнение

= 1 -

Возведем обе части уравнения в квадрат:

()² =(1- )²

4х - 1=1-2 + 4х² - 1

4х-1=4х²-2

Снова возведем обе части уравнения в квадрат:

(4х-1)²=(4х-2)²

16х-4=16х⁴-8х²(4х+1)+(4х+1)²

16х-4-16х⁴+8х²(4х+1)-(4х+1)²=0

16х⁴-32х³+8х²-8х+5=0

Далее воспользуемся теоремой Безу:

Делители 16: ±1,±2,±8…

Делители 5: ±1, ±2, ±5 . . .

Свободный коэффициент 1/2

16х⁴-32х³+8х²-8х+5 х-1/2

16х⁴-8х³ 16х³-24х²-4х-10

-24х³+8х²-8х+5

-24х³+12х²

-4х²-8х+5

-4х²+2х

-10х+5

-10х+5

0

Теперь уравнение можно представить следующим образом

(х- ½) (16х³-24х²-4х-10)=0

х- ½ = 0 или 16х³-24х²-4х-10=0 │:2

8х³-12х² -2х-5=0

8х³=12х² +2х+5

Построим графики у=8х³ и у=12х² +2х+5 Графиком первой функции будет являться гипербола, а графиком второй - парабола, ветви которой направлены вверх. Из чертежа видно, что графики функций не пересекаются, а значит уравнение не имеет больше корней.

у=12х² +2х+5

у=8х³Значит, единственным корнем уравнения будет являться х= ½.

Ответ: х= ½.

Х

Теоремы, связанные с областью определения и областью значения функции.

Иногда знание области определения или области значения позволяет быстро и легко найти верное решение для уравнения.

Пример1.

Решить уравнение = log₅(x-3)

Решение.

Найдем ОДЗ.

3-х≥0

х-3>0

-х≥-3 | ·(-1)

х>3

x≤3

x>3

3

Решив ОДЗ, видим, что уравнение не имеет решений, значит решать и само уравнение не имеет смысла.

Ответ: .

Пример2.

Решить уравнение = + tgx

Решение.

Найдем ОДЗ данного уравнения.

sinx≥0

-sinx≥0 y

cosx≠0

sinx≥0

sinx≤0 x

cosx≠0

sinx=0

cosx≠0

Решением ОДЗ является х=πn, n Z.

Подставим это значение в уравнение:

= + tgπn , n Z.

= + 0

0 = 0 - верное равенство.

Значит, корнем уравнения является х=πn, n Z.

Ответ: х=πn, n Z.

Метод мажорант.

Основная идея метода мажорант состоит в следующем:

Если мы имеем уравнение f(x) = g(x) и существует такое число φ, что для любого х из области определения f(x) и g(x) имеем f(x) ≤φ и g(x)≥φ. Тогда уравнение f(x) = g(x) равносильно на множестве φ системе уравнений:

g(x)=φ

f(x) =φ

Этот метод называют методом Мажорант (от франц. Majorante, majorer - объявлять бо́льшим).

Метод мажорант - это метод нахождения ограниченности функции.

Мажорирование - это нахождение точек ограничения функции.

Пример 1.

Решить уравнение x²+3 = cosx + 2

Решение.

x²+3 = cosx + 2

x² +1 = cosx

y=x² + 1 : E(f) х²≥0 x² + 1=1

х²+1≥1 cosx=1 x=0

y = cosx : E(f) -1≤cosx≤1

Рассмотрим области значения функций у= x² +1 и у= cosx. Т.к. на области значений у этих функций есть общая точка (т.е. 1) значит данное уравнение равносильно системе уравнений cosx=1

x² + 1=1

второе уравнение имеет только один корень х=0, подставляя это значение в первое уравнение, получаем верное числовое равенство, значит, корнем уравнения является 0.

Ответ: x=0

Пример 2.

Решить уравнение log₃(x² + 4x +13) = cosπx - sin

Решение.

Найдем области значений данных функций

log₃(x² + 4x +13) ≥2, т.к. x² + 4x +13≥9, т.к. log₃9=2

cosπx - sin≤2, т.к. cosπx≤1 и - sin≤1

Т.к. первая функция больше или равна двух, а вторая меньше или равна двух, то данное уравнение равносильно системе уравнений

log₃(x² + 4x +13) =2

cosπx - sin≤2

Первое уравнение имеет только один корень х=-2, подставляя это значение во второе уравнение, получаем верное числовое равенство. Следовательно, корнем уравнения является -2.

Ответ: х=-2

Пример3.

Решить уравнение 4^Х+(х-13)*2^Х- 2х+22=0

Решение.

2^2Х+(х-13)*2^Х- 2х+22=0 - квадратное уравнение относительно 2^Х, где a=1, b=x-13,

c= - 2x+22.

Пусть 2^Х= t, тогда

t²+(x-13)t - 2x +22=0

D=b²-4ac

D=(x-13)²-4*1*(-2x+22)= x²-26x+169 - 4(-2x+22)=x²-26x+169+8x-88= x²-18x+81=(x-9)²

t_1,2 =

t₁= = 2, x>0

= -x +11, x<0

t₂= = = = 2, x>0

= -x+11, x<0

Таким образом, 2^X=2

2^X=11-x

В первом уравнении находим, что х=1 - является единственным корнем этого уравнения, т.к. у=2^X - возрастающая, а 2=const и 2¹=2

2= 2 - верное равенство.

Во втором уравнении у=2^X - возрастающая, а у= 11- х - убывающая, значит это уравнение имеет не более одного корня. Подбором находим х=3.

2³=11-3

8 = 8 - верное равенство

Ответ: х=1, х=3.

Пример4.

Решить уравнение 2sinx=5x²+2x+3

Решение.

Найдем области значений функций.

1.у = 2sinx

-1≤ sinx ≤1

-2≤ 2sinx ≤2

2. y= 5x²+2x +3 - парабола, ветви которой направлены вверх, значит минимум этой функции будет достигнут в точке Х_{вершины.} Х _в= , Х_в = = - 0,2.

Значит правая часть будет не меньше, чем у=5*(- 0,2)²+2 *(- 0,2) +3 = 2

Таким образом, левая часть не превосходит 2, а правая не меньше, чем 2. Значит, мы доказали, что левая часть уравнения строго меньше правой при любом х, то есть решений для данного уравнения нет.

Ответ:

Пример 5.

Решите уравнение log₂(x²+4) - log₂x = 4x - x² -2

Решение.

log₂()= 4x - x² - 2 ОДЗ х²+4>0

х>0

Найдем области значений функций.

1. Т.к. х²+4 ≥ 4, то log₂ () ≥2

2)При любом х: 4х- х²-2 = 2- (х² - 4х +4) = 2-(х-2)²

2-(х-2)²≤2

Таким образом, данное уравнение равносильно системе уравнений

log₂()

4x - x² - 2 = 2

Решим второе уравнение:

4x - x² - 2 = 2

-х²+4х-2-2=0 | · (-1)

х²-4х+4=0

(х-2)²=0

х-2=0

х=2

Оно имеет корень х=2, подставляя это значение во второе уравнение, получаем верное числовое равенство. Следовательно, единственны корнем уравнения является 2.

Ответ: х=2

Эту теорему выгодно применять тогда, когда аналитическим способом решить уравнение очень сложно.

Пример6.

Решить уравнение х²+2х+3=

Решение.

Найдем области определения обеих функций:

1. f(x)= х²+2х+3 = х²-2х+1+2=(х²-1)+2

0≤(х²-1)≤

2≤(х²-1)+2≤

2. g(x)=

0≤≤2

Таким образом, единственное решение возможно, когда f(x)=g(x) =2, но f(x)=2 при х=-1, а g(x)=2 при х=0. Эти значения не совпадают, значит, для данного уравнения решений нет.

Ответ:

Заметим, что решить аналитическим способом данное уравнение проблематично:

х²+2х+3=

(х²+2х+3)²=()²

((х²+3)+2х)²=()²

((х+3)²+4х(х²+3)+4х²-4+х²=0

х⁴+6х²+9+4х³+12х+4х²-4+х²=0

х⁴+4х³+11х²+12х+5=0

Решение получается очень длинным и сложным. Поэтому более выгодно использовать теорему, основанную на ограниченности функции.

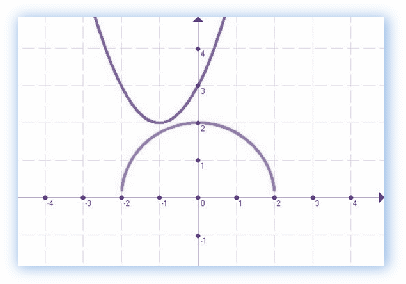
Решим это же уравнение графическим способом. Построим графики функций у= х²+2х+3 и у=. Графиком первой функции является парабола, ветви которой направлены вниз, а графиком второй функции парабола, ветви которой направлены вверх. Построим графики.

х

-1

0

1

2

3

у

6

3

2

3

6

у=х²+2х+3

х

-2

-1

0

1

2

у

0

1,7

2

1,7

0

у=

Решением уравнения должна быть абсцисса точки пересечения графиков. Но из чертежа видно, что графики не пересекаются. Значит для данного уравнения решений нет, что и было доказано при решении данного уравнения с использованием теоремы, основанной на ограниченности функции.

Ответ: Решений нет.

У

у=х²+2х+3

Пример7.

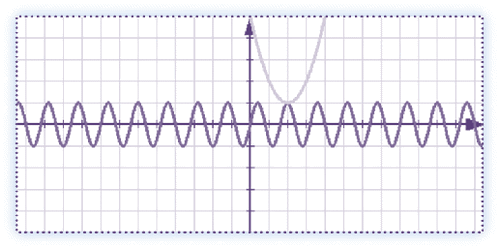
ХГрафически решим уравнение sinx ⁼ x² - 4x + 5.

Построим графики функций

у= sinx

и у= x² - 4x + 5. Графиком первой функции является синусоида с периодом 1,5, а графиком второй функции является парабола, ветви которой направлены вниз.

Построим графики.

У

у= x² - 4x + 5Корнем уравнения

будет являться

абсцисса точки пересечения этих

функций. Очевидно,

Х

2что это 2.

Значит, корнем уравнения будет являться 2.

Но в данное уравнение проще решить, если использовать теорему , основанную на ограниченности функции.

Ведь иногда не просто построить график.

Решим данное уравнение, применяя теорему, основанную на ограниченности функции.

1. у= x² - 4x + 5 - парабола, ветви которой направлены вверх, значит своего минимума парабола будет достигать в точке с координатами (Х_{вершины} ; У_{вершины}), т.е.

Х_в= Х_в==2, У_в=Х²в - 4Хв +5, У_в=4 -4*2+5 = 1 в точке с координатами (2;1).

2. -1≤sin≤1

Таким образом, уравнение равносильно системе уравнений

x² - 4x + 5=1

sin = 1

Второе уравнение имеет единственный корень равный 2. Подставляя это значение во второе уравнение, получаем верное числовое равенство. Значит, корнем уравнения будет являться х=2.

Ответ: х=2.

Пример8.

Решить уравнение 2^Х + = 3

Решение.

Приведем уравнение к виду 2^Х = 3 - и построим графики уравнений у=2^Х и у=3 - .

х

-3

-2

-1

0

1

2

у

1/8

1/4

1/2

1

2

4

у=2^Х,

х

0

1

4

9

у

3

2

1

3

, у=3 - .

у=2^Х

У

Решением уравнения является абсцисса точки пересечения графиков. Из чертежа видно, что абсциссой точки пересечения является х=1.

Ответ: х=1.

Х

Вывод:

Таким образом, при решении уравнений иногда очень полезно применять свойства функции, учитывая сформулированные теоремы. Я думаю, что разобранные в ходе данной работы задачи убедительно демонстрируют эффективность функционально графического метода при решении уравнений.

Список используемой литературы.

1. И.Ф.Шарыгин, В.И.Голубев

«Факультативный курс по математике. Решение задач».

Москва, издательство «Просвещение», 1991 год.

2. В.Н.Матвеев, Н.М.Матвеев

«Сборник задач по математике».

Издательство Казанского университета, 1968 год.

3. М.Л.Галицкий, М.М.Мошкович, С.И.Шварцбурд

«Углубленное изучение курса алгебры и математического анализа»

Москва, издательство «Просвещение», 1986 год.

4. П.И.Горштейн, В.Б.Полонский, М.С.Якир

«Задачи с параметрами»

Москва - Харьков, издательства «Илекса», «Гимназия», 2002 год.

5. В.В.Ткачук

«Математика - абитуриенту»

Москва, издательство МЦНМО, 2002 год.

6. Сборники ЕГЭ.