Три пути ведут к знанию:

путь размышления-это путь

самый благородный,

путь подражания-это путь

самый легкий

и путь опыта-это путь

самый горький.

Конфуций

Тема урока: Линейные однородные дифференциальные уравнения второго порядка

Цели урока:

Образовательная

Систематизировать , расширять знания и умения учащихся, связанные с применением методов решения дифференциальных уравнений второго порядка;

2) Развивающая

Развивать: а) умение анализировать математические ситуации ;

б) умение выделять главное;

в) умение сравнивать, обобщать, классифицировать ;

3) Воспитывающая

Побуждать учащихся к преодолению трудностей в процессе умственной деятельности, самоанализу своей деятельности;

Тип урока: комбинированный

Оборудование урока: интерактивная доска, лист успешности учащегося, деформированные задания, тест

Вся работа на уроке сопровождается индивидуальным листом успешности

Лист успешности учащегося

Фамилия, Имя___________________________________________________

Ход урока:

I. Постановка целей урока

II. Актуализация опорных знаний

1) Закончить формулировку определения:

1. Уравнения, связывающие независимую переменную, искомую функцию и ее производные называются….(дифференциальными)

2. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называют …..(обыкновенным)

3. Функция , которая при подстановке в уравнение, обращает его в тождество называется….(решением уравнения)

4. Наивысший порядок производной, входящей в дифференциальное уравнение называется…(порядком уравнения)

5. Уравнение вида F(х,у,)=0 называется …..(диф. уравнением 1-го порядка)

6. Уравнение вида f(x,y)dx=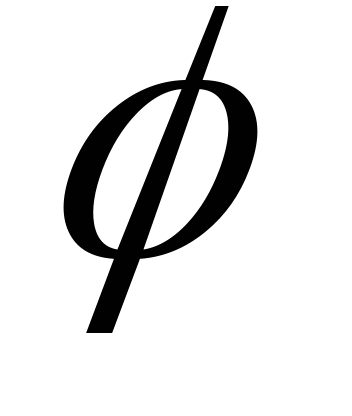(x,y)dy называется…..(однородным)

7. Уравнение вида = f₁(x) f₂₍y) называется…..(диф. уравнением с разделяющимися переменными)

8. Уравнение вида +Р(х)у=Q(x) называется…..(линейным диф. уравнением 1-го порядка)

9. Уравнение вида F(х,у, , )=0 называется…(диф. уравнением второго порядка)

10. Процесс отыскания решения диф. уравнения называется….(итегрированием)

2) Классификация дифференциальных уравнений по их видам:

1

ДУ с разделяющимися переменными. =sin2x

2. (6у+3)dx=2dy

Линейное ДУ первого порядка

3. (x²-y²)dx+2xydy=0

4

ДУ третьего порядка.

5. +2+6y=0

Однородное ДУ первого порядка

6. =3x² -4x+2cos3x

Линейное однородное ДУ второго порядка

ДУ второго порядка

3) Классификация дифференциальных уравнений по методам их решения

dx - xdy =0

4

1. Метод четырехкратного интегрирования

2

(1+x²) -xy=2x

5

2. Метод разделения переменных

3

2

3. Метод двукратного интегрирования

4

=6x⁴-12x²+

3

4. Метод сведения ДУ к уравнению с разделяющимися переменными

5

y=2cos2x

1

5. Метод подстановки у=uv

6

+4+8y=0

6

6. Метод замены ДУ характеристическим уравнением

4) Алгоритм нахождения общего решения линейного однородного уравнения второго порядка

Чтобы найти общее решение линейного однородного уравнения второго порядка

нужно:

Если k₁k_2, то

у=c₁e^kx+c₂e^kх

1

Если k_{1 =} k₂, то

у= е^kx(c₁ +c₂x)

2

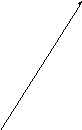
Если k₁ и k₂ - комплексные числа, то у=е^ах(с₁cosbx +c₂sinbx)

3

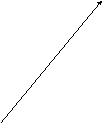
Заменить у¹¹, у¹, у на k², k,1

4

5

Составить характеристическое уравнение вида: k²+px+q=0

III. Формирование практических умений и навыков:

1) Найти ошибку в решении дифференциального уравнения третьего порядка:

= 9х²+4-2 cos4x

= 3x³+4x- sin4x+c₁

=

y=

2) Найти пары: «Уравнение-его решение»

у=е(с₁+с₂х)

Б

у=с₁е+с₂е^-6х

В

у=е(с₁+с₂х

Г

у=с₁+с₂е^9х

1

+8+16у=0

+

2

-+у=0

+

3

-9=0

+

4

+5-6у=0

+

3) Решить дифференциальные уравнения с комплексными корнями:

а) +4+8у=0 б) -2+2у=0

k²+4k+8=0 k2 -2k+2=0

Д=16-32=-16 Д= -4

Д¹=Д/4= -4 k_1/2= - Д¹=Д/4= -1

k_1/2= -2 k_1/2= 1

y=e^-2x(c₁cos2x+c₂sin2x) y=e^x(c₁cosx+c₂sinx)

IV. Выполнение теста

1 вариант

1. Уравнение -4у-3=0- это уравнение:

А) с разделяющимися переменными; Б) линейное диф. уравнение 1-го порядка;

В) однородное уравнение 1-го порядка; Г) диф. уравнение 2-го порядка;

2. Уравнение (х²-у²)dy-(xy-y²)dx=0 - это уравнение:

А) с разделяющимися переменными; Б) линейное диф. уравнение 1-го порядка;

В) однородное диф. уравнение ; Г) диф. уравнение 2-го порядка;

3. Найти общее решение диф. уравнения:

А) у=е^х(c₁cos2x+c₂sin2x) Б) у=е^4х(с₁cosx+c₂sinx) В) у=е^2х(c₁cos3x+c₂sin3х) Г)у=е^4х(с₁cos2x+c₂sin2x)

А) у=е^х(c₁+c₂x) Б) у=е^-х(с₁+c₂x) В) у=е^2х(c₁+c₂x) Г) у=е^4х(с₁+c₂x)

А) у=е^х(c₁cos2x+c₂sin2x) Б) у=е^4х(с₁cosx+c₂sinx) В) у=е^2х(c₁cos3x+c₂sin3x) Г) у=е^-3х (с₁cosx+c₂sinx)

2 вариант

1. Уравнение - - это уравнение:

А) с разделяющимися переменными; Б) линейное диф. уравнение 1-го порядка;

В) однородное уравнение 1-го порядка; Г) диф. уравнение 2-го порядка;

2. Уравнение 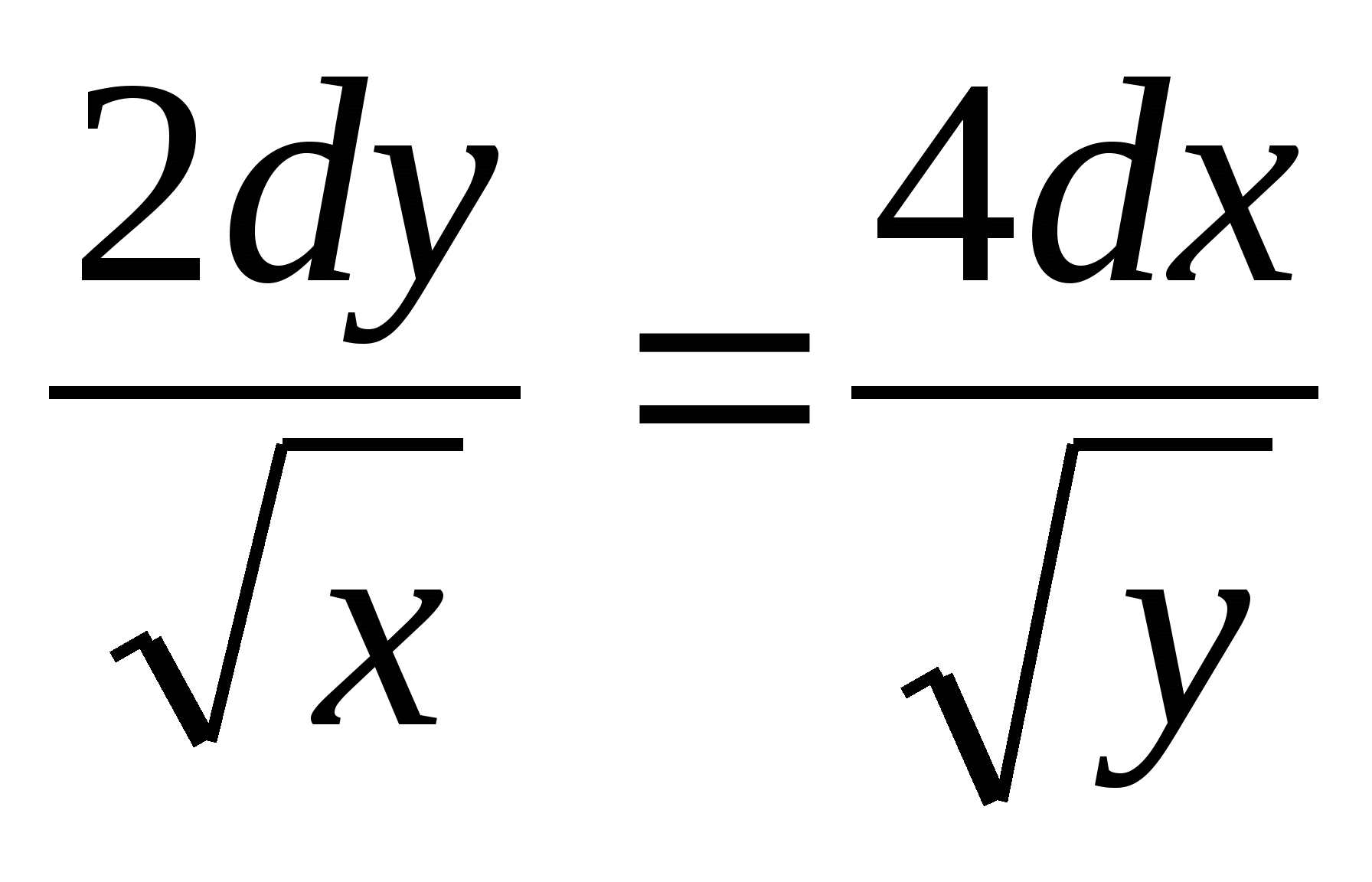- это уравнение:

А) с разделяющимися переменными; Б) линейное диф. уравнение 1-го порядка;

В) однородное уравнение ; Г) диф. уравнение 2-го порядка;

2. Найти общее решение диф. уравнения:

А) у=е^х(c₁cos2x+c₂sin2x) Б) у=е^-4х (с₁cos2x+c₂sin2x) В) у=е^2х(c₁cos3x+c₂sin3х) Г)у=е^4х(с₁cos2x+c₂sin2x)

А) у=е^х(c₁+c₂x) Б) у=с₁е^2х+c₂е^4х В) у=c₁е^х+c₂е^-4х Г) у=е^4х(с₁+c₂x)

А) у=е^х(c₁cos2x+c₂sin2x) Б) у=е^4х(с₁cosx+c₂sinx) В) у=е^-х(c₁cosx+c₂sinx )

Г) у=е^-3х (с₁cosx+c₂sinx)

Ключи к тесту:

Вариант

1

2

3

4

5

1

Б

В

В

Б

Г

2

Б

А

Б

В

В

V. Домашнее задание:

1. Составить три диф. уравнения третьего порядка и три диф. уравнения четвертого порядка;

2. Решить эти уравнения;

6. Рефлексия, итоги урока