Тема урока: Простые задачи на построение

Дата: 09.04

Тема урока: Простые задачи на построение

Цель урока: Формирование умений анализировать изученный материал и навыков применения его для решения задач; показать значимость изучаемых понятий; развитие познавательной активности и самостоятельности получения знаний;

Задачи урока: решение задач на построение

Ход урока:

1 этап: орг момент, приветствие, проверка дом задания

2 этап: новая тема

Пример: Построение угла, равного данному

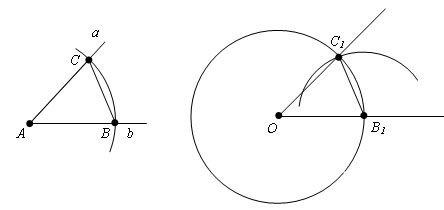
Пример: Построить биссектрису данного угла.

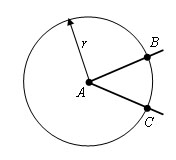
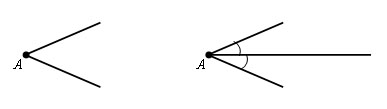
Решение

Из вершины A данного угла как из центра описываем окружность произвольного радиуса r. Пусть B и С - точки ее пересечения со сторонами угла.

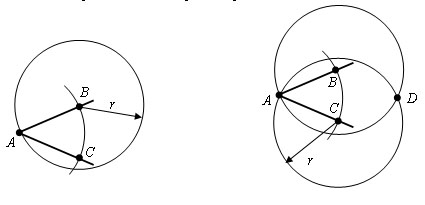
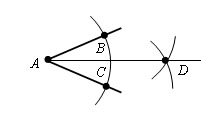
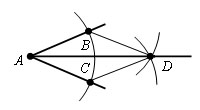
Из точек В и С проведем окружности тем же радиусом r. Пусть точка D - точка их пересечения отличная от A. Проведем луч AD.

Проведем отрезки BD и CD. Δ ABD = Δ ACD, по третьему признаку равенства треугольников. Отсюда ∠ BAD = ∠ CAD и следовательно AD - биссектриса угла BAC.

Пример: деление отрезка пополам

3 этап: чертежи к заданиям

№ 233 стр 74 - ОКРУЖНОСТЬ

№ 232 стр 74 - ОКРУЖНОСТЬ

Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определённым свойством. Например, окружность, можно определить как геометрическое место точек, равноудалённых от данной точки.

№ 234 стр 74

Найдите геометрическое место центров окружностей, проходящих через две данные точки.

Решение: Пусть окружность с центром O проходит через данные точки A и B. Поскольку OA = OB (как радиусы одной окружности), точка O лежит на серединном перпендикуляре к отрезку AB. Обратно, каждая точка O, лежащая на серединном перпендикуляре к AB, равноудалена от точек A и B. Значит, точка O - центр окружности, проходящей через точки A и B.

№ 235 стр 74

Это будет прямая параллельная данной

4 этап: подведение итогов

5 этап домашнее задание № 236 № 237