План-конспект урока по геометрии 'Аксиома параллельных прямых' (7 класс)

План - конспект урока геометрии в 7 классе по теме :

«Аксиома параллельных прямых»

Учитель: Сёмина О.В.

Психолого - педагогическая характеристика 7 класса

В 7 классе 8 учащихся : 6 мальчиков и 2 девочки. Комплектование класса происходило по заявлениям родителей. Состав класса стабильный. По уровню интеллектуальных способностей класс можно разделить на две группы.

У шести учащихся ( Алексеев А., Кох О., Габрикевич М., Устинов Н., Савченко А., Чеменева Н.) средний уровень развития. Внимание произвольное, объем, концентрация и устойчивость средние. Преобладает механическая память. Для поддержания внимания необходимо использовать смену деятельности, интересные факты, наглядные пособия. Эти дети не сразу усваивают учебный материал. Для усвоения нужно еще один - два раза повторить нужные определения, правила, выводы. Они не всегда видят, выделяют признаки, анализируют, сравнивают, находят различия, классифицируют, обобщают. Часто им необходима помощь учителя. У них больше развито практическое мышление. Эти дети мало читают. Творческие задания у них вызывают затруднения.

Два ученика (Угляница Ю. и Филатов М.) имеют низкий уровень развития. У этих детей процесс понимания, решения, ответа опережает процессы обдумывания, анализа. Внимание произвольное. Объем, концентрация и устойчивость низкие. Отсутствует способность к длительной и стойкой сосредоточенности. Быстро появляется утомление. Слуховая, Зрительная и моторная память не прочны. Эта группа учащихся нуждается в постоянном напоминании, индивидуальной помощи и контроля со стороны учителя. У них слабо развита речь, небольшой словарный запас, они не могут объяснить свой выбор решения. Задания выполняют только по образцу.

В целом класс работоспособный, всегда есть на кого опереться.

ЦЕЛИ:

ОБРАЗОВАТЕЛЬНЫЕ:

- Дать представление об аксиомах и аксиоматическом методе в геометрии;

- ввести аксиому параллельных прямых;

- помочь учащимся самостоятельно прийти к выводу, что аксиомы имеют большое значение при доказательстве теорем и решении геометрических задач.

РАЗВИВАЮЩИЕ:

- Ознакомить учащихся с вопросами истории , связанными с пятым постулатом Евклида и геометрией Лобачевского;

- развивать навыки самостоятельной работы с учебником и дополнительной литературой;

- развивать активность мышления;

- формировать познавательные способности.

ВОСПИТАТЕЛЬНЫЕ:

- Содействовать рациональной организации труда;

- воспитание сознательного отношения к учебе.

ОБОРУДОВАНИЕ:

- портреты Евклида и Н. Лобачевского;

- Научные статьи о Евклиде и Н. Лобачевском;

План урока

1. Оргмомент.

2. Сообщение темы и цели урока.

3. Актуализация опорных знаний.

4. Объяснение нового материала.

5. Закрепление полученных знаний.

6. Домашнее задание.

7. Подведение итогов урока.

8. Выставление оценок.

Ход урока

Содержание урока

Теоретическое обоснование

1. Оргмомент.

- Здравствуйте, ребята и уважаемые гости! Ребят я попрошу занять свои места, быть очень внимательными и активными. Откройте тетради, запишите сегодняшнее число и классная работа.

2. Сообщение темы и цели урока.

- Сегодня на уроке мы с вами узнаем, что означает красивое слово «аксиома» и познакомимся с одной из самых известных аксиом геометрии - аксиомой параллельных прямых. А также узнаем, кто из великих математиков внес бесценный вклад в дело изучения этой проблемы.

3. Актуализация опорных знаний.

1) Перекрестный опрос.

Учащиеся по очереди задают вопросы друг другу по предыдущей теме.

2) Решение по готовым чертежам.

А) Параллельны ли прямые а и b, изображенные на рисунке?

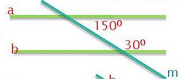
Б) На рисунке точка О -

Середина отрезков ЕА

и КВ. Докажите, что

ЕВ//КА.

4. Объяснение нового материала.

А) Объяснение учителя.

- Изучая свойства геометрических фигур, мы доказали ряд теорем. При этом мы опирались, как правило, на доказанные теоремы. А на чем основаны доказательства самых первых теорем геометрии? Ответ на этот вопрос такой:

Некоторые утверждения о свойствах геометриче-ских фигур принимаются в качестве исходных по-ложений, на основе которых доказываются далее теоремы и, вообще, строится вся геометрия. Такие исходные положения называются аксиомами. Само слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».

( Обратить внимание на плакаты с высказывания-ми, повешенные перед уроком на доску. 1) «Аксиома - полная недоказуемость, равная полной не-опровержимости» А. Круглов 2) «Аксиома - это истина, на которую не хватило доказательств» В. Хмурый )

С некоторыми аксиомами мы уже знакомились, хотя и не называли их аксиомами. Например, аксиомой является утверждение о том, что через любые две точки проходит прямая, и притом только одна. Многие другие аксиомы, хотя и не были выделены особо, но фактически использовались в наших рассуждениях. Так, сравнение двух отрезков мы проводили с помощью наложения одного отрезка на другой. Возможность такого наложения вытекает из следующей аксиомы: на любом луче от его начала можно отложить от-резок, равный данному, и притом только один.

Сравнение двух углов основано на аналогичной аксиоме: от любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.

Все эти аксиомы являются наглядно очевидными и не вызывают сомнений. Полный список аксиом планиметрии, принятых в нашем курсе геометрии, приводятся в конце учебника.

Такой подход к построению геометрии, когда сначала формулируются исходные положения - аксиомы, а затем на их основе путем логических рассуждений доказываются другие утверждения, зародился еще в глубокой древности и был изложен в знаменитом сочинении «Начала» древнегрече-ского ученого Евклида.

( примерно 365 - 300 гг. до н. э.).

Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в курсах геометрии, а сама геометрия, изложенная в «Началах», называется евклидовой геометрией.

Б)Сообщение ученика о Евклиде.

- Об этом поразительном человеке история со-хранила настолько мало сведений, что нередко высказывают сомнения в самом его существо-вании. Что же дошло до нас? Евклид был со-временником царя Птолемея 1, который цар-ствовал с 306 по 283 г. до н.э. Он преподавал в Александрии, столице Птолемея 1, начинавшей превращаться в один из центров научной жизни. Евклид был последователем древнегреческого философа Платона, и преподавал арифметику, геометрию, теорию гармонии, астрономию. Ве-личайшая заслуга Евклида в том, что он подвел итог построению геометрии и придал изложению столь совершенную форму, что на две тысячи лет «Начала» стали энциклопедией геометрии. Евклид с величайшим искусством расположил материал по 13 книгам. Они не дошли до нас в подлиннике, но изложенная в них геометрия считалась образцом, которому стремились следовать ученые.

В) Сообщение учителя.

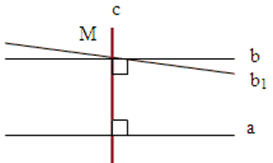
Рассмотрим произвольную прямую а и точку М, не лежащую на ней. Докажем, что через точку М можно провести прямую, параллельную прямой а. Для этого проведем через точку М две прямые: сначала прямую с перпендикулярно к прямой а, а затем прямую в перпендикулярно к прямой с. Так как прямые а и в перпендикулярны к прямой с, то они параллельны.

Итак, через точку М проходит прямая в, параллельная прямой а.

- Можно ли через точку М провести еще одну прямую, параллельную прямой а ?

Нам представляется, что если прямую в «повернуть» даже на очень малый угол вокруг точки М, то она пересечет прямую а . Иными словами, нам кажется, что через точку М нельзя провести другую прямую ( отличную от в ), параллельную прямой а.

А можно ли это утверждение доказать?

Этот вопрос имеет большую историю. В «Началах» Евклида содержится постулат ( пятый по-стулат Евклида ), из которого следует, что через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Многие математики , начиная с древних времен, предпринимали попытки доказать пятый постулат Евклида, т.е. вывести его из других аксиом. Однако эти попытки каждый раз ока-зывались неудачными. И лишь в 19в. Было окончательно выяснено, что это утверждение не может быть доказано на основе других аксиом Евклида, а само является аксиомой.

Огромную роль в решении этого вопроса сыграл великий русский математик Николай Иванович Лобачевский.

Г) ВЫСТУПЛЕНИЕ УЧЕНИКА.

- Вся творческая жизнь нашего выдающегося соотечественника была связана с Казанским университетом, где он учился, затем был про-фессором, а с 1828 г. - ректором университета. Его очень рано заинтересовала геометрия, и он, как и многие его предшественники, пытался до-казать пятый постулат Евклида. В результате изысканий им был сделан замечательный вы-вод: можно построить другую геометрию, от-личную от геометрии Евклида. Такая геометрия им была построена. Ее называют геометрией Лобачевского. Сообщение об открытии новой геометрии было сделано Лобачевским в 1826 г.

5. Решение на закрепление.

№ 196 - устно

№ 197 - самостоятельно, с последующей

проверкой у доски.

( На рисунке показать учащимся два

возможных случая расположения прямых:

а) все четыре прямые пересекают прямую р;

б) одна из четырех прямых параллельна

прямой р, а три другие прямые пересекают

ее.

Утверждения, которые выводятся непосред-ственно из аксиом или теорем, называются следствиями. Рассмотрим некоторые следствия из аксиомы параллельных прямых.

1⁰. Если прямая пересекает одну из двух па-раллельных прямых, то она пересекает и другую.

Дано: а//в, прямая с пересекает прямую а в точке М.

Доказать: прямая с пересекает и прямую в.

Док-во: Если бы прямая с не пересекала прямую в, то через точку М проходили бы две прямые (прямые а и с), параллельные прямой в. Но это противоречит аксиоме параллельных прямых, и, значит, прямая с пересекает прямую в.

2⁰. Если две прямые параллельны третьей прямой, то они параллельны.

№ 198

6. Объяснение домашнего задания.

Домашнее задание дифференцированное.

1) Учащимся с низким уровнем развития.

П.27, 28.(прочитать; аксиому и следствия - выучить), № 199.

2) учащимся со средним уровнем развития.

П.27, 28 ( прочитать; аксиому и следствия - выучить; знать доказательства следствий),

№ 199; стр. 296-298(читать; найти формулировку 5 постулата Евклида).

7. Подведение итогов урока.

- Что нового узнали? Чему научились?

- И в завершении нашего урока я хочу прочитать стихотворение Вл. Михайловского

«Пути параллелей»

…Вечность тайну тебе нашептала,

и умом изумленным постигнул ты то,

Что доселе не знал и не ведал никто:

Параллели стрелою нацелены ввысь.

Параллели пронзают межзвездные дали,

Параллели - ты слышишь! - стремятся сойтись,

Только сразу такое постигнешь едва ли.

- Чушь, -кричат ,- Лобачевский-нелепица, бред!

Ничего смехотворней и в мире-то нет.

Параллели не встретятся - это же просто.

Ну хоть рельсы возьми: пересечься им, что ли?

- Не понять им: коль к звездам протянутся

рельсы -

Справедливы там будут иные законы -

Параллели, сливаясь, спешат в бесконечность.

8. Выставление оценок.

Создание эмоцио-нального настроя, направленного на концентрацию вни-мания. Снятие напряженности, тревожности.

Повышение познава-тельного интереса. Быстрое включение класса в деловой ритм. Организация внимания всех уча-щихся. Подготовка учащихся к активной работе на уроке.

Закрепление, уточнение и систематизация знаний учащихся. Контроль со стороны учителя.

Постановка проблемы

Дается представ-ление об аксио-мах.

Развитие познава-тельного интереса.

Расширить представление об аксиомах геометрии.

Повышение познава-тельного интереса через исторические сведения.

Повышение познава-тельного интереса. Развитие умения ра-ботать с дополни-тельной справочной литературой.

Изложение нового материала. Доказать существование прямой, проходящую через данную точку и параллельную данной прямой.

Постановка пробле-мы. Подведение учащихся к самосто-ятельному выводу.

Постановка пробле-мы. Ее решение че-рез сообщение исто-рических сведений.

Развитие познавательного интереса.

Развитие умения работать с дополнительной литературой. Организация внимания учащихся.

Развитие умения выступать перед аудиторией.

Закрепление полу-ченных знаний. Обу-чение умению ис-пользовать получен-ные знания. Развитие умения работать са-мостоятельно.

Объяснение нового материала.

Развитие умения рассуждать и дока-зывать.

Закрепление полученных знаний.

Дифференцированное домашнее задание с учетом уровня обучаемости.

Развивать умение работать с дополнительной литературой.

Обобщение знаний, умений, навыков.

Создание позитивного настроя.

Необходимое поощрение учащихся за работу на уроке.

Самоанализ урока.

Тема урока «Аксиома параллельных прямых». По плану это четвертый урок по изучаемой главе «Параллельные прямые».

Исходя из особенностей класса, образовательные цели можно сформулировать так: 1) дать представление об аксиомах и аксиоматическом методе в геометрии; 2) ввести аксиому параллельных прямых; 3) помочь учащимся самостоятельно прийти к выводу, что аксиомы имеют большое значение при доказательстве теорем и решении геометрических задач. Образовательный аспект позволяет поставить такие развивающие цели, как 1) ознакомить учащихся с вопросами истории, связанными с пятым постулатом Евклида и геометрией Лобачевского; 2) развивать навыки самостоятельной работы с учебником и дополнительной литературой; 3) развивать активность мышления и формировать познавательные способности. В воспитательном аспекте считаю необходимым содействовать рациональной организации труда и воспитанию сознательного отношения к учебе.

Все запланированные цели были реализованы на уроке.

Исходя из целей урока, было запланировано 8 структурных компонентов урока.

1. ОРГМОМЕНТ - Обеспечение нормальной обстановки на уроке, создание эмоционального настроя, направленного на концентрацию внимания.

2. СООБЩЕНИЕ ТЕМЫ И ЦЕЛИ УРОКА - Цель этого этапа - повысить познавательный интерес; быстрое включение класса в деловой ритм; организация внимания учащихся. Перед учащимися ставится проблема.

3. АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ - Закрепить, уточнить и систематизировать знания учащихся.

4. ОБЪЯСНЕНИЕ НОВОГО МАТЕРИАЛА - Повысить познавательный интерес через сообщение исторических сведений. Дать представление об аксиомах и аксиоматическом методе в геометрии. Развивать умение рассуждать и доказывать, выступать перед аудиторией.

5. ЗАКРЕПЛЕНИЕ ПОЛУЧЕННЫХ ЗНАНИЙ - Закрепить знания, полученные на уроке. Развивать умение рассуждать и доказывать.

6. ДОМАШНЕЕ ЗАДАНИЕ носит дифференцированный характер.

7.8. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. ВЫСТАВЛЕНИЕ ОЦЕНОК. Итог проходит в виде вопросно-ответной беседы. Данный этап урока призван создать у детей чувство удовлетворения своей работой, атмосферы значимости.

Список используемой литературы:

1. Геометрия: учеб. Для 7 - 9 кл. общеобразоват. Учреждений / Л. С. Атанасян и др. - 10-е изд. - М.: Просвещение, 2010.

2. Изучение геометрии в 7 - 9 классах: Метод. Рекомендации к учеб.:Кн. Для учителя / Л. С Атанасян и др. - М.: Просвещение, 2010.

3. Энциклопедический словарь юного математика/Сост. А. П. Савин. - М.: Педагогика, 1989.

4. Предметные недели в школе. Математика./ Сост. Л.В. Гончарова. - Волгоград. Изд. «Учитель», 2001.