Разработка урока в 5 классе на тему: «Сравнение десятичных дробей»

ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ В 5 КЛАССЕ

Школа: МБОУ «Гимназия №4, г. Пушкино».

Учитель математики: Полежаева Ирина Николаевна.

Класс: 5 "а"

Дата проведения:

Урок № 3. «Сравнение десятичных дробей», п.22

Цель: ознакомить обучающихся с алгоритмом сравнения десятичных дробей; научить выполнять сравнение с опорой на алгоритм; развивать умение сравнительного анализа.

Базовый учебник: Математика. 5 кл.: учеб. для общеобразоват. учреждений /Г.К.Муравин, О.В.Муравина.- М.: Дрофа,2012.

Формы работы: устная, фронтальная, самостоятельная, групповая.

Тип урока: Урок изучения нового материала.

Методы: словесные, наглядные и практические, проблемный, беседа, самостоятельная работа.

Оборудование: мультимедийный проектор.

Основные виды учебной деятельности (на уровне учебных действий): учащийся научится сравнивать и упорядочивать десятичные дроби.

1 этап.

Фронтальный опрос.

Что такое десятичная дробь?

Чем десятичные дроби отличаются от обыкновенных дробей?

Для чего нам нужны десятичные дроби?

Как изображают десятичную дробь на координатном луче? Например, десятичную дробь 0,8.

Устный счет.

Прочитайте дроби:

0,125 23,004

51,012 21,45

2,78 5,05

8,0006 14,078

0,000021 1,002

Математический диктант

Запиши в виде десятичной дроби:

Пять целых семь десятых

Сорок две целых пятьдесят две сотых

Одна целая три сотых

Две целых пять тысячных

Ноль целых сто шесть тысячных

Взаимопроверка (5,7; 42,52; 1,03; 2,005; 0,106)

2 этап. Математическое лото. (Учащиеся представляют обыкновенные дроби в виде десятичных дробей, открывают нужный квадрат, в итоге открывается картинка)

Используемые ЦОР

Математическое лото

files.school-collection.edu.ru/dlrstore/aa834f7f-17ca-44ef-aa04-3f71627978d0/%5BM56_5-04%5D_%5BQS_06-01%5D.html</</p>

Учащиеся формулируют тему урока, определяют цели урока.

3 этап. Объяснение нового материала.

1) равные дроби;

2) сравнение десятичных дробей на координатном луче;

3) сравнение десятичных дробей по их разрядам.

Проблема: по рисункам сравните обыкновенные дроби и сделайте вывод как сравнить десятичные дроби.

Давайте вместе попробуем разобраться, как же сравниваются десятичные дроби. Чуть позже мы обязательно вернемся к нашим ученикам и спортсменам, а сейчас поработаем со следующими примерами:

Сравнить дроби

а) 2,3 и 12,1; б) 2,1 и 2,3;

в) 2,11 и 2,14; г) 2,11 и 2,4.

Попробуем подробно разобраться с каждой парой дробей.

Какие есть мысли по поводу сравнения первой пары чисел?

Верно, количество целых у второй дроби больше, чем у первой, значит, 12,1 > 2,1.

Какой вывод можно сделать?

Молодцы, сначала смотрим на количество целых. Больше будет та дробь, у которой больше целых.

Вторая пара дробей. Как их сравнить?

Правильно, целых одинаковое количество, но десятых у второй дроби больше, чем у первой, значит, 2,1 < 2,3. Вывод?

Верно, если целых одинаковое количество, смотрим на десятые, больше будет та дробь, у которой десятых больше.

Третья пара дробей. Как сравнить? Молодцы, если целых и десятых одинаковое количество, значит, смотрим на сотые, больше будет та дробь, у которой сотых больше. Значит,

2,11 < 2,14.

На самом деле, уже стало понятно, что, если сотых одинаковое количество, то смотрим на тысячные и т.д.

А как сравнить 2,11 и 2,4?

Совершенно верно некоторые из вас заметили, что у числа 2,4 количество десятых больше, чем у числа 2,11, значит, 2,4 > 2,11.

Давайте попробуем убедиться в этом, чтобы не было сомнений.

Какие дроби мы умеем сравнивать?

Верно, обыкновенные, но любые ли?

Верно, только с одинаковыми знаменателями.

Как бы нам применить наши знания в этом примере?

Молодцы, можно записать число 2,4 как 2,40 и сравнить по уже знакомому правилу числа.

Итак, мы с вами разобрали все возможные случаи сравнения десятичных дробей.

Учащиеся формулируют правило сравнения десятичных дробей по их разрядам.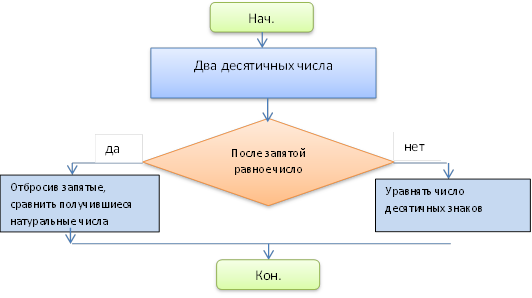

4 этап. Физкультминутка.

Из - за парт мы выйдем дружно,

Но шуметь совсем не нужно,

Встали прямо, ноги вместе,

Поворот кругом, на месте.

Хлопнем пару раз в ладошки.

И потопаем немножко.

А теперь представим, детки,

Будто руки наши - ветки.

Покачаем ими дружно,

Словно ветер дует южный.

Ветер стих. Вздохнули дружно.

Нам урок продолжить нужно.

Подравнялись, тихо сели

И на доску посмотрели.

5 этап. Выполнение учащимися заданий на закрепление пройденного правила.

Задача 1. На зимней Олимпиаде в соревнованиях по конькобежному спорту спортсмены финишировали со следующими результатами:

Спортсмен А - 41,13 сек;

Спортсмен Б - 40,8 сек;

Спортсмен В - 40,72 сек;

Кто из спортсменов самый быстрый? Самый медленный? Какие места заняли спортсмены в итоговой турнирной таблице?

(учащиеся отвечают на вопросы учителя)

Молодцы, теперь мы уверенно и правильно ответили на эти вопросы.

Потренируемся еще. (Решают задачи с учебника у доски)

Сравнить дроби:

I вариант. II вариант.

12,567 и 125,67; 4,199 и 4,2;

7,399 и 7,4; 18,342 и 183,42;

0,0091 и 0,01. 0,02 и 0,0045.

Учащиеся решают примеры по вариантам самостоятельно в тетради, от каждого варианта к доске выходит по одному человеку, решают те же примеры на боковых досках, потом вместе с классом проверяют.

Если все решено верно, ставим себе 5 баллов в лист оценивания за самостоятельную работу, если верно решено два примера, ставим себе 4 балла, за один верно решенный пример ставим себе 3 балла.

6 этап. Рефлексия:

1) Как сравниваются десятичные дроби?

2) Чему вы научились на уроке?

3)Трудно ли сравнивать десятичные дроби?

4)Понравился ли вам урок?

5) Оцените свою работу на уроке.

7 этап. Домашнее задание №669,№667.

При выполнении 3 этапа используются познавательные УУД: логические: сравнение, анализ, выведение следствий из требования; постановка и решение проблемы.

При выполнении 5 этапа используются познавательные УУД (уметь решать примеры по выбранному правилу; применение предметных знаний, выбор способов решения задач) регулятивные (умение проговаривать последовательность действий на уроке, анализировать и оценивать результат работы), коммуникативные (умение слушать, обращаться с вопросом к учителю и сверстнику), личностные: самооценка.