Урок математики в 8 классе по теме 'Косинус угла'.

Учитель математики

МБОУ ЛСОШ №2 им Н.Ф.Струченкова

Л.Ф.Бесшабашнова

Тема урока. Косинус угла.

Цели: путем исследования ввести определение косинуса острого угла в прямоугольном треугольнике, научить обучающихся пользоваться соотношениями между сторонами и углами прямоугольного треугольника ; развивать наблюдательность, внимательность, познавательный интерес к предмету; воспитание у обучающихся трудолюбия, взаимоуважения.

Тип урока: изучение нового материала и первичного закрепления.

Ход урока.

l.Организационный момент.

ll.Проверка домашнего задания.

Домашнее задание дифференцированное.Самопроверка .

lll.Актуализация знаний.

1.Сформулировать теорему Фалеса.(Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки. то они отсекают равные отрезки и на другой стороне угла.)

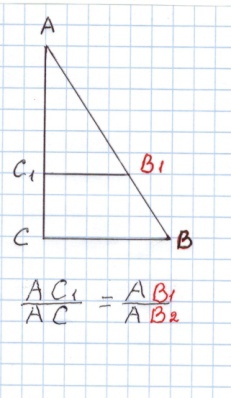
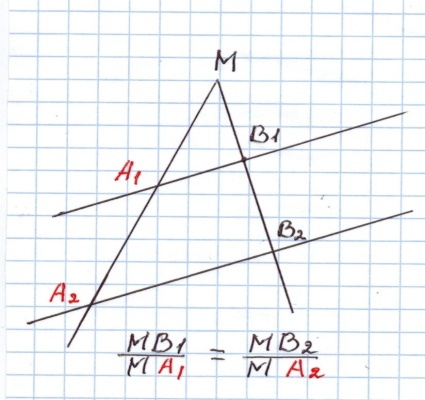
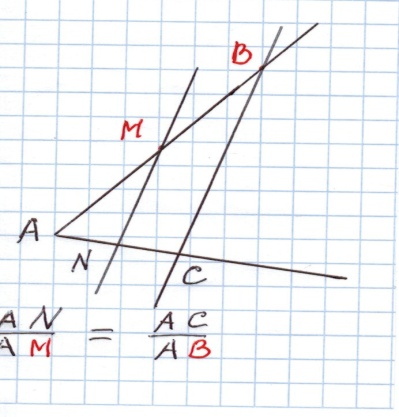
2.Сформулируйте теорему о пропорциональных отрезках.(Параллельные прямые ,пересекающие стороны угла , отсекают от сторон угла пропорциональные отрезки)

3.Какой треугольник называется прямоугольным?

4.Как называются стороны прямоугольного треугольника?

lll .Изучение нового материала.

1.Ввести понятие прилежащего катета. Работа с альбомом (Различное расположение прямоугольных треугольников).Назвать катет, прилежащий к названному острому углу.

2.Вопрос. «Не хотели бы вы, ребята, сами начертить прямоугольные треугольники, но такие, чтобы у каждого из вас был совершенно оригинальный рисунок»

Обозначим один из острых углов 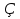,выделим одним цветом прилежащий катет, а другим гипотенузу. Цвета выбираются такими же, как в предыдущей устной работе.

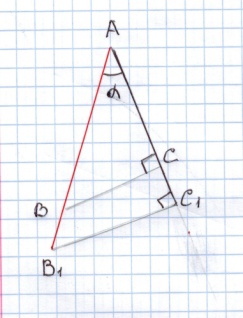
Измерить с точностью до 0,1 гипотенузу и катет, прилежащий к углу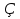 , затем найти отношение этого катета к гипотенузе и записать его в тетради.

Предлагается увеличить рисунок. Продолжить катет, прилежащий к углу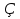 ,В конце получившегося отрезка проведём перпендикуляр к нему до пересечения с продолжением гипотенузы. Во вновь построенном треугольнике измерим катет, прилежащий к углу 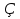и гипотенузу и найдём отношение катета к гипотенузе. Как странно у нас , снова получается то же число, что и раньше! Просто волшебное число!

Число это называется косинус! Дети записывают тему урока. Кто может дать определение этому понятию. Уточняя и исправляя друг друга дети дают определение косинуса.

Ввести обозначение косинуса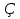

Историческая справка. Термин косинус ввел английский математик и астроном Эдмунт Гентер в 1620 г.Но этот термин не получил немедленного признания со стороны известных математиков того времени. Появился в работах математиков в 1633,1635, 1671 г.Обозначение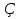 впервые применил Бернули в 1739 г.

3.Вернемся к нашим вычислениям. Дети называют свои числа:0,5;0,7;0,6; 0,5….

Сравнить свои рисунки и объяснить, почему же так получилось. От чего же зависит наше число?(от величины угла)Ответы получились разные? В чем дело? Мы сравнивали углы на глаз? Надо измерять! Но это не удовлетворяет нас. Нельзя верить своим глазам, когда речь идет о геометрии. Измерения тоже подводят. Надо доказывать!

4.Теорема.Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.

lV.Закрепление изученного материала.

1).

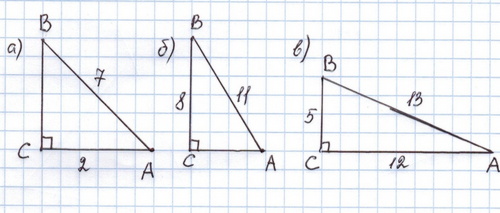
а)Чему равен ?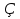

б)Косинус какого угла можно вычислить по этим данным?

в)Чему равен 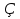и ?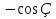

2).В прямоугольном треугольнике катет равен 8 см, а косинус прилежащего угла равен 0,8.

Чему равна гипотенуза?

3).В прямоугольном треугольнике АВС катет ВС равен 7 см. Высота СD,опущенная из вершины прямого угла С, отсекает отрезок ВD равный 3 см.Чему равна гипотенуза?

4).На стороне угла А отложены отрезки АВ=BD=DF=5см. Из точек В, D, F опущены перпендикуляры на другую сторону угла.АС=3см.Вычислите косинус угла А :а) из треугольника АВС; б) из треугольника АDF; в) из треугольника АFG.

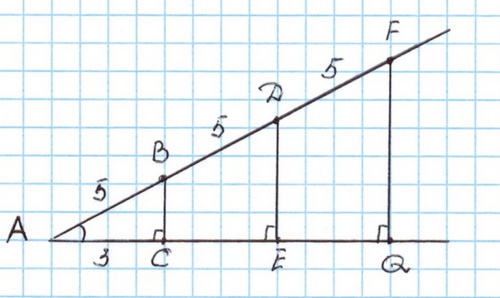
Вывод: Равные углы имеют равные косинусы.

V.Итог урока.

Vl .Задание на дом.

Задание получают дифференцированное.