Рабочая программа

по математике (алгебра) в 9 а классе

(базовый уровень)

на 2016- 2017 учебный год.

Учитель математики: Батталова В. Г.

2016 г.

Пояснительная записка.

Рабочая программа по алгебре в 9 классе составлена в соответствии с

1.Законом 273-ФЗ «Об образовании в Российской Федерации».

2.Федеральным компонентом Государственного стандарта основного общего и среднего (полного) общего образования.

3.Учебным планом МОБУ «СОШ №4» на 2016-2017 учебный год.

4.Федеральный перечень учебников, утвержденный приказом Минобрнауки РФ, рекомендованных (допущенных) к использованию в образовательном процессе в общеобразовательных учреждениях на 2016-2017 учебный год.

5. Программы общеобразовательных учреждений. Алгебра. 7-9 классы. / Сост. Бурмистрова Т.А. - М. «Просвещение», 2011 г.

Программа соответствует учебнику «Алгебра 9 класс» Ю.Н.Макарычев, Н.Г. Миндюк и др.; под редакцией С.А.Теляковского. М.: Просвещение,2011г.

Рабочая программа по алгебре в 9 классе рассчитана на 105 часа, из расчета 3 часа в неделю.

При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Арифметика», «Алгебра», «Элементы логики, комбинаторики, статистики и теории вероятностей».

Рабочая программа выполняет две основные функции.

Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.

Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.

Общая характеристика учебного предмета.

Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика, алгебра, геометрия, элементы комбинаторики теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека.

В ходе освоения содержания курса учащиеся получают возможность:

• развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

• овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

• изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

• получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

• развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

• сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Задачи:

● систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры; формирование и расширение алгебраического аппарата;

● формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности;

● получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов;

● формирование у школьников представлений о роли математики в развитии цивилизации и культуры;

● развитие представлений о вероятностно-статистических закономерностях в окружающем мире;

● совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развитие логического мышления.

Цели

Изучение алгебры в 9 классе направлено на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, способности к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Основные развивающие и воспитательные цели

Развитие:

• Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, способности к преодолению трудностей;

• Математической речи;

• Сенсорной сферы; двигательной моторики;

• Внимания; памяти;

• Навыков само и взаимопроверки.

Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.

Воспитание:

• Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;

• Волевых качеств;

• Коммуникабельности;

• Ответственности.

В ходе преподавания математики в 9 классе, работы над формированием у учащихся, перечисленных в программе знаний и умений, следует обратить внимание на то, чтобы они овладевали умениями обще учебного характера, разнообразными способами деятельности, приобретали опыт:

-методами исследования реального мира, умения действовать в нестандартных ситуациях;

-решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

-исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

-ясного, точного, грамотного изложения своих мыслей в устной и письменной речи;

-использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации;

-проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

-поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

Математическая компетенция-способность структурировать данные (ситуацию), вычленять математические отношения, создавать математическую модель ситуации, анализировать и преобразовывать ее, интерпретировать полученные результаты. Математическая компетенция учащегося способствует адекватному применению математики для решения возникающих в повседневной жизни проблем. Готовность обучающегося самостоятельно работать с информацией различных источников, искать, анализировать и отбирать необходимую информацию, организовать, сохранять и передавать ее. Формировать учебно -познавательную компетентность- готовность обучающегося к самостоятельной познавательной деятельности: целеполаганию, планированию, анализу, рефлексию, самооценке учебно-познавательной деятельности, владению измерительными навыкам.

Учебно - тематическое планирование.Раздел

Количество часов в рабочей программе

Количество контрольных работ

1. Квадратичная функция.

23

2

2. Уравнения и неравенства с одной переменной

14

1

3Уравнения и неравенства с двумя переменными.

17

1

4 Арифметическая и геометрическая прогрессии.

15

2

5. Элементы комбинаторики и теории вероятностей

10

1

6. Повторение

26

1

ИТОГО

105

8

Содержание тем учебного предмета. (105 часов)

Тема 1. Квадратичная функция (23 ч)

Функция. Область определения и область значений функции. Свойства функций. Квадратный трехчлен и его корни. Разложение квадратного трехчлена на множители.

Квадратичная функция и ее график. Функция у = х. Корень п-ой степени.

В результате изучения данной темы обучающийся должен знать/понимать: определение квадратного трехчлена, формулировку теоремы о разложении на множители квадратного трехчлена; определение степенной функции с натуральным показателем; свойства степенной функции с четным и нечетным показателем; определение корня п-ой степени с рациональным показателем;

уметь: выделять квадрат двучлена из квадратного трехчлена; раскладывать трехчлен на множители, если есть корни; схематически изображать график функции у=х при различных п и описывать свойства; вычислять значение корня п-ой степени; упрощать выражения со степенями.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: чтения графиков функций, решения несложных алгебраических задач.

Уровень обязательной подготовки выпускника

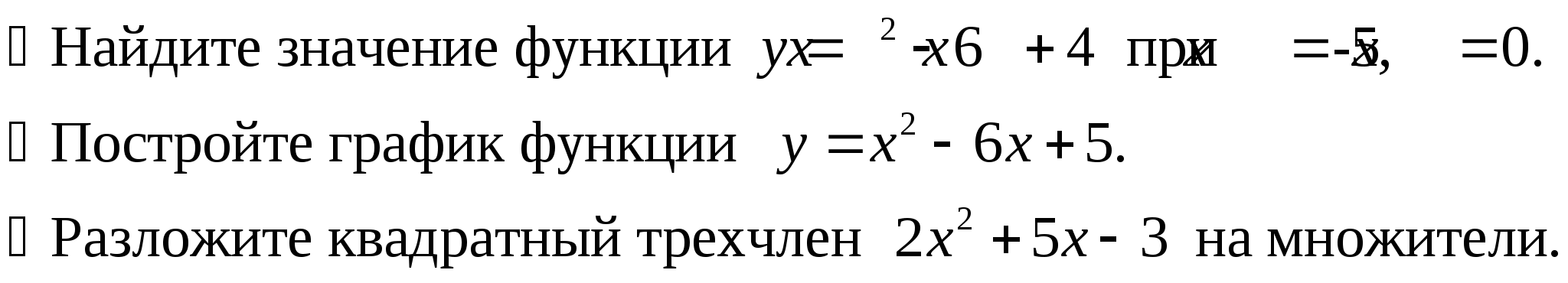
Уровень возможной подготовки выпускника

Тема 2. Уравнения и неравенства с одной переменной (14 ч)

Целое уравнение и его корни. Дробные рациональные уравнения. Решение неравенств второй степени с одной переменной. Решение неравенств методом интервалов.

В результате изучения данной темы обучающийся должен знать/понимать: понятия целого рационального уравнения; способы разложения многочлена на множители; определение биквадратного, дробно-рационального уравнений; алгоритм решения дробно-рациональных уравнений; определение неравенства 2-ой степени с одной переменной; графический способ решения неравенств (алгоритм); метод интервалов;

уметь: определять виды уравнений; владеть различными способами разложения многочлена на множители; применять алгоритм решения дробно-рациональных уравнений для их решения; определять неравенства 2-ой степени с одной переменной; применять графический способ для их решения; применять метод интервалов.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: решения целых рациональных, биквадратных, дробно-рациональных уравнений.

Уровень обязательной подготовки выпускника

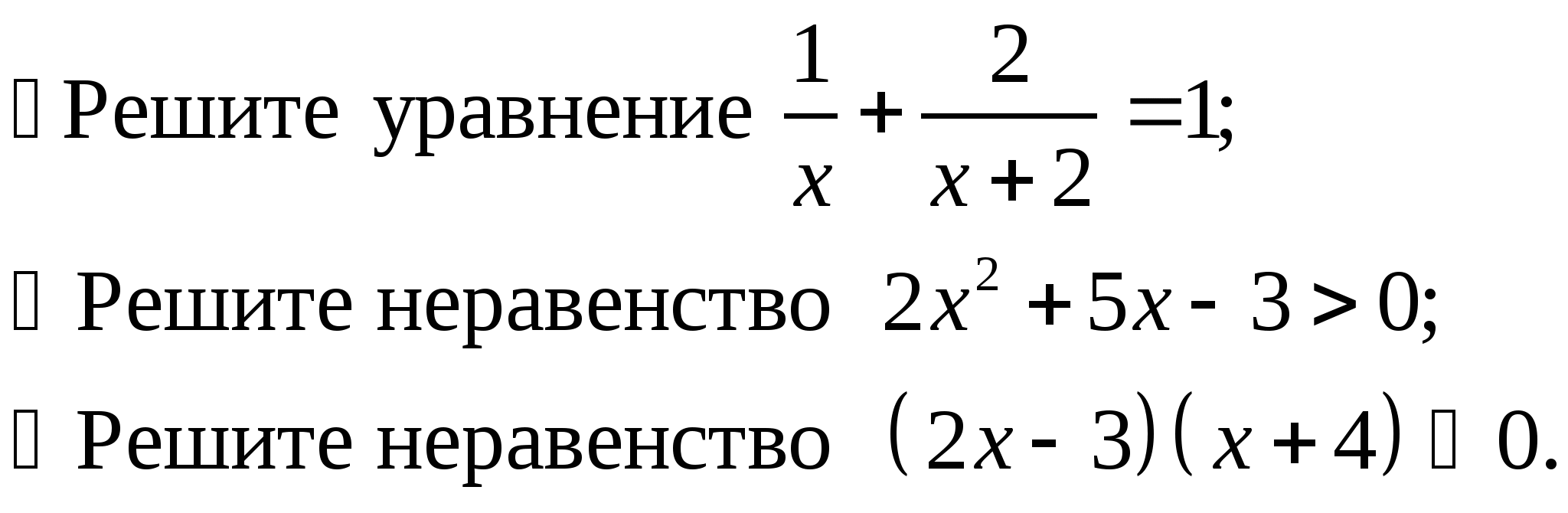
Уровень возможной подготовки выпускника

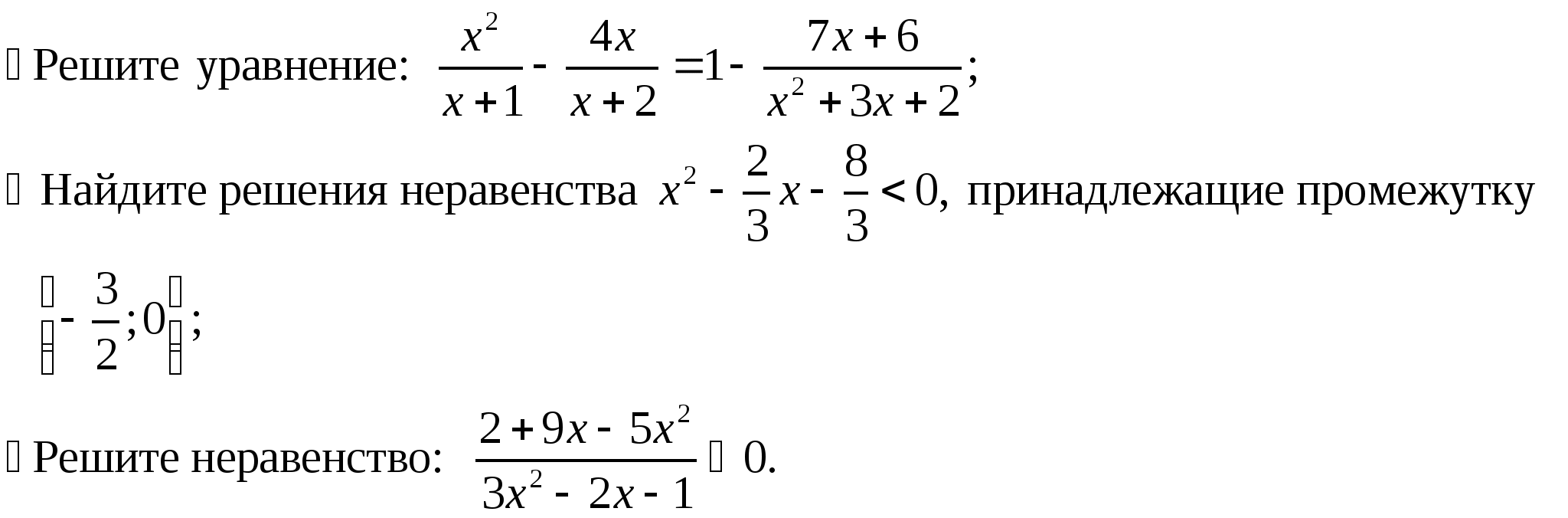
Тема 3. Уравнения и неравенства с двумя переменными (17ч)

Уравнения с двумя переменными и его график. Графический способ решения систем уравнений. Решение систем уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными. Системы неравенств с двумя переменными.

В результате изучения данной темы обучающийся должен знать/понимать: определение решения уравнения с двумя переменными; определение графика уравнения с двумя переменными; что значит решить систему уравнений второй степени, (алгоритм решения); определение решения неравенств с двумя переменными; решение системы неравенства с двумя переменными; множества решений некоторых систем неравенств с двумя переменными и их систем.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: решения уравнений, систем уравнений и систем неравенств с двумя переменными.

Уровень обязательной подготовки выпускника

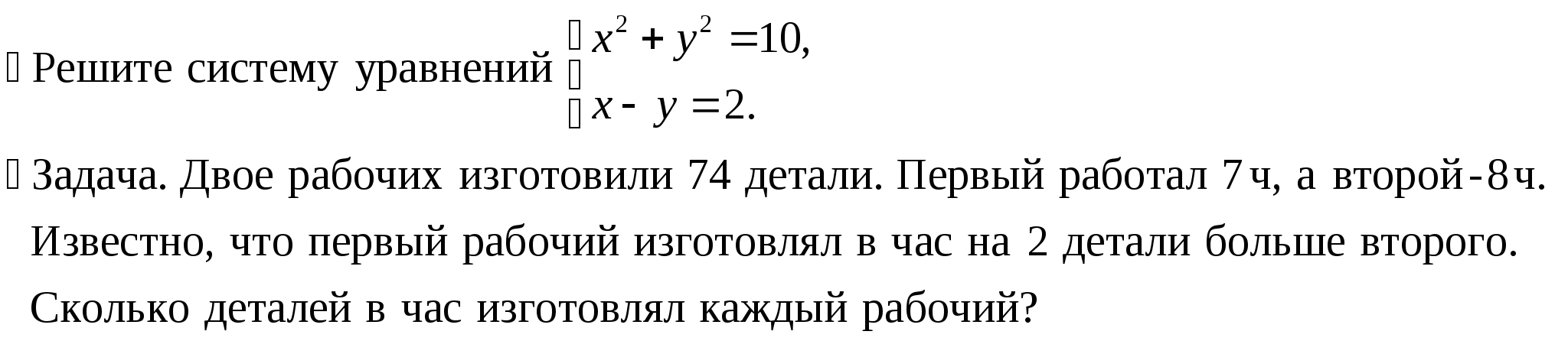
Уровень возможной подготовки выпускника

Тема 4. Арифметическая и геометрическая прогрессии (15 ч)

Последовательности. Определение арифметической прогрессии. Формула п-го члена арифметической прогрессии. Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии. Формула суммы первых п членов геометрической прогрессии.

В результате изучения данной темы обучающийся должен знать/понимать: понятие последовательности; смысл понятия «п-й» член последовательности; определение арифметической и геометрической прогрессий; определение разности арифметической прогрессии и знаменателя геометрической прогрессий; формулы п-го члена и суммы п - членов арифметической и геометрической прогрессий; характеристика свойства арифметической и геометрической прогрессий;

уметь: использовать индексное обозначение; применять формулы п-го члена и суммы п-членов арифметической и геометрической прогрессий для выполнения упражнений.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни: для решения задач.

Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника

Тема 5. Элементы комбинаторики и теории вероятности (10 ч)

Примеры комбинаторных задач. Перестановки. Размещения. Сочетания. Относительная частота случайного события. Вероятность равновозможных событий.

В результате изучения данной темы обучающийся должен знать/понимать: комбинаторное правило умножения; определение перестановок, размещений, сочетаний; понятия отношений частоты и вероятности случайного события; формулы для подсчета их числа; понятия «случайное событие», «относительная частота», «вероятность случайного события»;

уметь: различать понятия «размещение» и «сочетания»; определять о каком виде комбинаций идет речь в задачах; решать задачи, в которых требуется составлять те или иные комбинации элементов и подсчитать их число; вычислять вероятность случайного события при классическом подходе.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: решения комбинаторных задач.

Уровень обязательной подготовки выпускника

• Сколькими способами могут разместиться 6 человек в салоне автобуса на шести свободных местах?

• Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 3, 4, 5?

• Из 12 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать такой выбор?

• Какова вероятность того, что при бросании игрального кубика выпадет более 4 очков?

Уровень возможной подготовки выпускника

• Из 20 вопросов к экзамену Вова 12 вопросов выучил, 5 совсем не смотрел, а в остальных что-то знает, а что-то нет. На экзамене в билете будет три вопроса.

а) Сколько существует вариантов билетов?

б) Сколько из них тех, в которых Вова знает все вопросы?

в) Сколько из них тех, в которых есть вопросы всех трех типов?

г) Сколько из них тех, в которых Вова выучил большинство вопросов?

• Случайным образом одновременно выбирают две буквы из 33 букв русского алфавита. Найдите вероятность того, что:

а) обе они гласные;

б) среди них есть буква «ь»;

в) среди них нет буквы «а»;

г) одна буква гласная, а другая согласная.

Комплексное повторение (26ч).

Раздел математики.

• Числа и вычисления.

• Выражения и преобразования.

• Уравнения и неравенства.

• Функции.

Требования к уровню подготовки обучающихся.

В результате изучения алгебры выпускник основной школы должен

знать/понимать

• существо понятия математического доказательства; приводить примеры доказательств;

• существо понятия алгоритма; приводить примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.

Арифметика

уметь

• выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;

• переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;

• выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;

• округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;

• пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;

• решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами.

Использовать приобретенные знания и умения в практической деятельности и

повседневной жизни для:

• решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;

• устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;

• интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.

Алгебра

уметь:

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;

• решать линейные и квадратные неравенства с одной переменной и их системы,

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• изображать числа точками на координатной прямой;

• определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;

• распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;

• описывать свойства изученных функций, строить их графики.

Использовать приобретенные знания и умения в практической деятельности и

повседневной жизни для:

• выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

Элементы логики, комбинаторики, статистики и теории вероятностей

уметь

• проводить несложные доказательства, получать простейшие следствия из известныхили ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;

• извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

• решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;

• вычислять средние значения результатов измерений;

• находить частоту события, используя собственные наблюдения и готовые статистические данные;

• находить вероятности случайных событий в простейших случаях.

Использовать приобретенные знания и умения в практической деятельности и

повседневной жизни для:

• выстраивания аргументации при доказательстве и в диалоге;

• распознавания логически некорректных рассуждений;

• записи математических утверждений, доказательств;

• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• решения учебных и практических задач, требующих систематического перебора вариантов;

• сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;

• понимания статистических утверждений.

Формы контроля.

Основными видами классных и домашних письменных работ обучающихся являются обучающие работы.

По алгебре в 9 классе проводятся текущие и одна итоговая письменные контрольные работы, самостоятельные работы, контроль знаний в форме теста. На четвертом уроке проводится входная контрольная работа, рассчитанная на урок. Учащиеся смогут подготовиться к ней на уроках и за счёт часов неаудиторной занятости.

Текущие контрольные работы имеют целью проверку усвоения изучаемого и проверяемого программного материала. На контрольные работы отводится 1 час. Контрольная работа №8 - итоговая, на неё отводится 3 часа.

Итоговая контрольная работа проводится в конце учебного года.

Самостоятельные работы и тестирование рассчитаны на часть урока (15-25 мин), в зависимости от цели проведения контроля.

Формы контроля ЗУН (ов):

• наблюдение

• беседа

• фронтальный опрос

• опрос в парах

• практикум

• самостоятельная работа

• тестирование

• письменная контрольная работа

Виды контроля:

ФО - фронтальный опрос.

ИРД - индивидуальная работа у доски.

ИРК - индивидуальная работа по карточкам.

ИК - индивидуальный контроль.

СК - самоконтроль.

ВК - взаимоконтроль.

СР - самостоятельная работа.

ПР - проверочная работа.

МД - математический диктант.

Т - тестовая работа.

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

допущено более одной ошибки или более двух, удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• допущены более одной ошибки или более двух- трех недочетов в выкладках, чертежах или графика, но учащийся владеет обязательными умениями по проверяемой теме.

• неполно раскрыто содержание материала (содержание изложено фрагментарно, недочеты в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

2. Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые

• Ответ оценивается отметкой «4», если общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

• незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

• незнание наименований единиц измерения;

• неумение выделить в ответе главное;

• неумение применять знания, алгоритмы для решения задач;

• неумение делать выводы и обобщения;

• неумение читать и строить графики;

• неумение пользоваться первоисточниками, учебником и справочниками;

• потеря корня или сохранение постороннего корня;

• отбрасывание без объяснений одного из них;

• равнозначные им ошибки;

• вычислительные ошибки, если они не являются опиской;

• логические ошибки.

3.2. К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

• неточность графика;

• нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

• нерациональные методы работы со справочной и другой литературой;

• неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

• нерациональные приемы вычислений и преобразований;

• небрежное выполнение записей, чертежей, схем, графиков.

Оценка устных ответов учащихся.

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;

• продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость использованных при ответе умений и навыков;

• отвечал самостоятельно без наводящих вопросов учителя.

Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.

• допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Отметка «3» ставится в следующих случаях:

• неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).

• имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при знании теоретического материала выявлена недостаточная сформированность умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Оценка «1» ставится в случае, если:

• ученик обнаружил полное незнание и непонимание изучаемого материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.

Оценка письменных контрольных работ учащихся.

Отметка «5» ставится в следующих случаях:

• работа выполнена полностью.

• в логических рассуждениях и обоснованиях нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала);

Отметка «4» ставится, если:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);

• допущена одна ошибка или два-три недочета в выкладках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);

Отметка «3» ставится, если:

• допущены более одной ошибки или более двух- трех недочетов в выкладках, чертежах или графика, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что учащийся не владеет обязательными знаниями по данной теме в полной мере.

Отметка «1» ставится, если:

• работа показала полное отсутствие у учащегося обязательных знаний, умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Перечень учебно-методического обеспечения:

Для учителя:

1. Т. А. Бурмистрова « Программа общеобразовательных учреждений. Алгебра. 7-9 классы» М. Просвещение, 2011г.

2. А.Н. Рурукин, С. А. Полякова. Поурочные разработки по алгебре к учебнику Ю. Н. Макарычева. Москва. Просвещение. «ВАКО». 2014год.

3. Учебник: Ю.Н. Макарычев, Н.Г. Миндюк « Алгебра. 9 класс», М.: «Просвещение», 2011г.

Для ученика:

1. Учебник: Ю.Н. Макарычев, Н.Г. Миндюк « Алгебра. 9 класс», М.: «Просвещение», 2011г.

2. Ю. Н. Макарычев «Дидактические материалы по алгебре для 9 класса», 2012 г

Дополнительная литература:

1. Т. М. Ерина «Поурочное планирование по алгебре» М.: «Просвещение», 2010.

2. П. Ершова « Самостоятельные и контрольные работы по алгебре и геометрии для 9 класса» М:Илекса, 2012

3. Л.Б. Крайнева « Сборник тестовых заданий для тематического и итогового контроля. Алгебра. 9 класс». М.: «Интеллект-Центр», 2011

4. Ю. Н. Макарычев «Дидактические материалы по алгебре для 9 класса». 2012г.

5. Глазков Ю.А., Варшавский И.К., Гаиашвили М.Я. Тесты К учебнику Ю.Н.Макарычева и др. Алгебра. 9 класс (3-е издание, 2011)

Для проведения промежуточного контроля используется:

1. Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра. 2014/ ФИПИ. - М.: Интеллект-Центр, 2014. - 128 с.

2. Алгебра. 9 класс. Тематические тесты для подготовки к ГИА - 2014. Учебно-методическое пособие/ Под ред. Ф.Ф. Лысенко. - Ростов н/Д: Легион - М, 2013. - 256 с.

3. Алгебра: сб. заданий для подгот. к гос. итоговой аттестации в 9 кл. /Л. В. Кузнецова, С. Б. Суворова, Е. А. Бунимович и др. - 4-е изд., перераб. - М.: Просвещение, 2013. - 240 с.: ил.

Адреса сайтов:

www.mathgia.ru

www.fipi.ru

www.prosv.ru

http:/www.drofa.ru

school-collection.edu.ru

Материальное техническое обеспечение уроков

Компьютер нашел свое место в каждой школе. Материально- техническая сторона компьютерной базы школ непрерывно улучшается. Все большее число учащихся осваивают первоначальные навыки пользователя компьютером. Однако в настоящее время недостаточное внимание уделяется разработке методик применения современных информационных технологий, компьютерных и мультимедийных продуктов в учебный процесс и вооружению частными приемами этой методики преподавателей каждого предметного профиля для каждодневной работы с учащимися. Цель создания данной рабочей программы - внедрение компьютерных технологий в учебный процесс преподавания геометрии в 8 классе.

Компьютерные технологии внедряются с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Применение анимации при создании такого компьютерного продукта позволяет рассматривать вопросы математической теории в движении, обеспечивает другой подход к изучению нового материала, вызывает повышенное внимание и интерес у учащихся.

При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.

В рабочей программе «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения, а также различные электронные учебники

• Демонстрационный материал (слайды).

Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Применение анимации при создании такого компьютерного продукта позволяет рассматривать вопросы математической теории в движении, обеспечивает другой подход к изучению нового материала, вызывает повышенное внимание и интерес у учащихся.

При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.

• Задания для устного счета.

Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель - ученик, взаимопроверки, а также в виде тренировочных занятий.

• Диски с видео уроками по алгебре 9 класса2014. Игорь Жаборовский. www.urokimatematiki.ru

Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.

Компьютерное обеспечение урока.

school-collection.edu.ru/ - единая коллекция цифровых образовательных ресурсов. Цифровые образовательные ресурсы (ЦОР) к учебникам. Ресурсы единой коллекции (Коллекции) цифровых образовательных ресурсов (ЦОР) могут использовать все участники образовательного процесса: учителя при подготовке и ведении занятий, учащиеся на уроках и при самостоятельных занятиях, методисты, разработчики учебно-методических материалов, работники органов управления образованием, родители. Коллекция представляет интерес для широкой общественности (для самообразования и других целей). Ресурсы Коллекции используются в учебном процессе как самостоятельно, так и в составе комплексных учебно-методических материалов. Всем заинтересованным участникам образовательного процесса предоставляется бесплатный и свободный (в техническом и правовом отношении) доступ к качественному и полному набору разнообразных учебных материалов, представленных в Коллекции.

www.prosv.ru - сайт издательства «Просвещение» (рубрика «Математика»)

www.math.ru -Интернет - поддержка учителей математики. Здесь можно найти электронные книги, видеолекции, различные по уровню и тематике задачи, истории из жизни математиков. Учителя найдут материалы для уроков, официальные документы Министерства образования и науки, необходимые в работе.

www.it-n.ru-Сеть творческих учителей. Создана для педагогов, которые интересуются возможностями улучшения качества обучения с помощью применения информационных и коммуникационных технологий (ИКТ). На этом веб-сайте вы найдете разнообразные материалы и ресурсы, касающиеся использования ИКТ в учебном процессе, а также сможете пообщаться со своими коллегами. На сайте для вас доступны:

- библиотека готовых учебных проектов с применением ИКТ, а также различные проектные идеи, на основе которых можно разработать свой собственный проект;

- библиотека методик проведения уроков использованием разнообразных электронных ресурсов;

- руководства и полезные советы по использованию программного обеспечения в учебном процессе;

- подборка ссылок на интересные аналитические и тематические статьи для педагогов.

www.exponenta.ru -Образовательный математический сайт. Содержит материалы по работе с математическими пакетами Mathcad, MATLAB, Mathematica, Maple и др. Методические разработки, примеры решения задач, выполненные с использованием математических пакетов. Форум и консультации для студентов и школьников.

http:/www.drofa.ru - сайт издательства Дрофа (рубрика «Математика»)

www.center.fio.ru/som - методические рекомендации учителю-предметнику (представлены все школьные предметы). Материалы для самостоятельной разработки профильных проб и активизации процесса обучения в старшей школе.

www.edu.ru - Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента, сервер информационной поддержки Единого государственного экзамена.

www.internet-scool.ru - сайт Интернет - школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, включают подготовку сдачи ЕГЭ.

www.legion.ru - сайт издательства «Легион»

www.intellectcentre.ru</<font face="Times New Roman, serif"> - сайт издательства «Интеллект-Центр», где можно найти учебно-тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений.

ФОРМЫ ОРГАНИЗАЦИИ УЧЕБНОГО ПРОЦЕССА

При организации учебного процесса будет обеспечена последовательность изучения учебного материала: новые знания опираются на недавно пройденный материал; обеспечено поэтапное раскрытие тем с последующей реализацией; закрепление в процессе практикумов, тренингов и итоговых собеседований; будут использоваться уроки-соревнования, уроки консультации, зачеты.

Формы организации учебного процесса:

• индивидуальные;

• групповые;

• индивидуально-групповые;

• фронтальные;

• практикумы.

Обще учебные умения, навыки и способы деятельности

В ходе изучения алгебры обучающиеся приобретают опыт:

• планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

• решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

• исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

• ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации,

интерпретации, аргументации и доказательства;

• проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

• поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

Сокращения, используемые в рабочей программе:

Типы уроков:

УОНМ - урок ознакомления с новым материалом.

УЗИМ - урок закрепления изученного материала.

УПЗУ - урок применения знаний и умений.

УОСЗ - урок обобщения и систематизации знаний.

УПКЗУ - урок проверки и коррекции знаний и умений.

КУ - комбинированный урок.

Календарно-тематическое планированиеТребования к уровню подготовки обучающихся

Контроль

знаний

учащихся

Количество

часов

Дата

Тип урока

ГЛАВА I. КВАДРАТИЧНАЯ ФУНКЦИЯ.

Цель: расширить сведения о свойствах функций, выработать умение строить график квадратичной функции и применять графическое представление для решения неравенств второй степени с одной переменной.

23

§1. ФУНКЦИИ И ИХ СВОЙСТВА.

Знать:

• прием нахождения приближенных корней;

• понятие квадратного трехчлена;

• формулу разложения квадратного трехчлена на множители;

• понятие функции и другие функциональные терминологии;

• понятия о возрастании и убывании функции, промежутках знакопостоянства;

• основные функции курса алгебры 7 - 8 классов и их свойства;

• понятия четной и нечетной функции.

Уметь:

• выделять квадрат двучлена из квадратного трехчлена;

• раскладывать трехчлен на множители;

• правильно употреблять функциональную терминологию, понимать ее в тексте, в речи учителя, в формулировке задач;

• находить значения функций, заданных формулой, таблицей, графиком и решать; решать обратную задачу;

• находить по графику промежутки возрастания и убывания функции, промежутки знакопостоянства, наибольшее и наименьшее значения.

5

1

2

Функция. Область определения и область значений функции, п.1.

ПР. СК, ВК, ИК.

2

02,04.09

УОНМ . Вводная и обзорная лекции.

3

4

5

Свойства функций, п.2.

МД.

СР, СК, ИК.

3

07,09, 11.09

УОНМ. Усвоение нового материала в процессе выполнения заданий.

§2. КВАДРАТНЫЙ ТРЕХЧЛЕН.

4

6

7

Квадратный трехчлен и его корни, п.3.

.ПР. СР. ГК, ИК. ДК.

2

14,16.09

УОНМ. Уроки практикумы.

8

9

Разложение квадратного трехчлена на множители, п.4.

Обучающая и контролирующая СР. Тренировочный тест (подготовка

к ГИА).

2

18,21.09

Лекция с примерами. УЗИМ. Практикум. УПЗУ.

10

Контрольная работа №1 по теме «Функции и их свойства. Квадратный трехчлен», п.п. 1 - 4.

Письменный контроль (ПК).

Фронтальный контроль (ФК).

1

23.09

Урок контроля и оценки знаний учащихся.

№

п/п

Раздел, название урока в

поурочном планировании

Требования к уровню подготовки обучающихся

Контроль

знаний

учащихся

Коли

чест

во ч.

Дата

Тип урока

§3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК.

Знать:

• свойства и особенности графиков функций y=ax², y=ax²+ n, y=a(x-m)², y=ax²+bx+c;

• свойства степенной функции при четном и нечетном натуральном показателе;

• график функции y=ax²+bx+c можно получить из графика функции y=ax² с помощью двух параллельных переносов;

• представление о нахождении значений корня с помощью микрокалькулятора;

• понятие корня п-ой степени; свойства корней n-ой степени.

Уметь:

• строить график квадратичной функции;

• выполнять простейшие преобразования графиков;

• указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы;

• находить по графикам квадратичной и степенной функций промежутки возрастания и убывания функции, промежутки, в которых функция сохраняет знак.

8

11

12

Функция y=ax² , ее график и свойства, п.5.

Проверочная и обучающая СР. ИК. ГК.

2

25,28.09

УОНМ. Исследование.

13

14

15

Графики функций y=ax²+ n, y=a(x-m)², п.6.

Проверочная СР. ИК.

3

30.09 02,05.10

УОНМ. Исследование. УЗИМ.

16

17

18

Построение графика квадратичной функции , п.7.

ПР.Проверочная СР. МД. Тренировочный тест (подготовка к ГИА).

3

07,09, 12.10

УОНМ. Исследование.

УЗИМ. УПЗУ.

§4. СТЕПЕННАЯ ФУНКЦИЯ. КОРЕНЬ п-ой СТЕПЕНИ.

4

Усвоение нового материала в процессе выполнения заданий.

19

Функция у=х^п, п. 8.

СР. СК. ИК.

1

14.10

20

Корень п-ой степени, п. 9.

ИК.

1

16.10

Комбинированный урок: лекция с элементами беседы, практикум,

21

Дробно-линейная функция и ее график, п. 10.

СК. Дифференцированный контроль.

1

19.10

Усвоение нового материала в процессе выполнения заданий.

22

Степень с рациональным показателем, п. 11.

МД проверочный.

СР. ИК.

1

21.10

УОНМ. Практикум.

23

Контрольная работа №2 по теме «Квадратичная функция»,

п.п. 5 - 11.

Письменный контроль. Фронтальный контроль (ФК).

1

23.10

Урок контроля и оценки знаний учащихся.

№

п/п

Раздел, название урока в

поурочном планировании

Требования к уровню подготовки обучающихся

Контроль

знаний

учащихся

Количество

ч.

Тип урока

ГЛАВА II. УРАВНЕНИЯ И НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ.

Цель: систематизировать и обобщить сведения о решении целых и дробных рациональных уравнений с одной переменной, сформировать умение решать неравенства вида или , где .

14

§5. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ.

Знать:

• понятие целого уравнения и его степени;

• основные методы решения целых рациональных уравнений.

Уметь:

• решать целые уравнения третьей и четвертой степени с помощью разложения на множители и введения вспомогательной переменной.

8

24

25

26

Целое уравнение и его корни, п.12.

Проверочная СР. ГК, ИК.

Тренировочный тест (подготовка к ГИА).

3

26,28, 30.10

Комбинированные уроки: лекция с элементами беседы, практикумы. УЗИМ.

УПЗУ.

27

28

29

30

31

Дробные рациональные уравнения, п. 13.

Знать:

• понятие дробного рационального уравнения, метода интервалов;

• основные методы решения целых рациональных уравнений, некоторые специальные приемы решения дробно-рациональных уравнений;

• понятие неравенств второй степени с одной переменной и методы их решений.

Уметь:

• применять графическое представление для решения неравенств второй степени с одной переменной;

• решать рациональные неравенства методом интервалов.

СР. ВК, СК, ИК.

5

9,11,13,

16,18.11

.

Усвоение нового материала в про-цессе выполнения заданий. УЗИМ. УПЗУ.

§6. НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ.

5

32

33

Решение неравенств второй степени с одной переменной,

п. 14.

Обучающая и контролирующая СР.

2

20,23.11

УОНМ. Практикум. Частично-поисковая деятельность.

34

35

Решение неравенств методом интервалов, п. 15.

ВК. ИК.

2

25,27.11

Практикум по решению задач.

36

Обобщающий урок.

Некоторые приемы решения целых уравнений, п. 16.

С Р с доп. литературой. Тренировочный тест (подготовка к ГИА).

1

30.11

Урок обобщения, систематизации знаний.

37

Контрольная работа №3 по теме «Уравнения и неравенства с одной переменной», п.п. 12 - 16.

Фронтальный письменный контроль.

1

02.12

Урок контроля и оценки знаний.

№

п/п

Раздел, название урока в

поурочном планировании

Требования к уровню подготовки обучающихся

Контроль

знаний

учащихся

Количество

ч.

Дата

Тип урока

ГЛАВА III. УРАВНЕНИЯ И НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ.

Цель: выработать умение решать простейшие системы, содержащие уравнений второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем.

17

§7. УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ.

Знать:

• понятия системы уравнений, неравенств с двумя переменными;

• уравнение окружности.

12

38

39

Уравнение с двумя переменными и его график, п.17.

СР. ИК

2

04,07.12

Уроки усвоения новых знаний и умений.

40

41

42

43

Графический способ решения систем уравнений, п.18.

СР. ГК, ИК.

4

09,11,12, 14.12

Усвоение новых знаний в процессе выполнения заданий. УЗИМ. УПЗУ.

44

45

46

47

Решение систем уравнений второй степени, п. 19.

ТК. ИК. ВК.

4

16,18,22, 21.12

УОНМ. Лекция с при-мерами. Практикумы по решению заданий.

УЗИМ. УПЗУ.

48

49

Решение задач с помощью уравнений второй степени, п. 20.

Уметь:

• решать текстовые задачи методом составления систем;

• решать системы уравнений методом подстановки, методов ведения вспомогательной переменной;

• решать графически системы уравнений;

• решать простейшие системы неравенств второй степени.

ВК. ИК.

2

23.15.12 11.01

УОНМ. Частично-поисковая деятельность.

§8. НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ.

4

50

51

Неравенства с двумя переменными, п. 21.

ВК. ИК. ГК.

2.

13.01

15.01

УОНМ. Комбинированные уроки. УЗИМ. УПЗУ.

52

Системы неравенств с двумя переменными, п. 22.

МД проверочный.

1

18.01

УОНМ. Практикум.

53

Обобщающий урок.

Некоторые приемы решения систем уравнений с двумя переменными, п. 23.

С Р с доп. литературой. Тренировочный тест (подготовка к ГИА).

1

20.01

Урок обобщения, систематизации знаний.

54

Контрольная работа №4 по теме «Уравнения и неравенства с двумя переменными», п.п. 17 - 23.

ПК. ФК. ИК.

1

22.01

Урок контроля и оценки знаний.

№

п/п

Раздел, название урока в

поурочном планировании

Требования к уровню подготовки обучающихся

Контроль

знаний

учащихся

Количество

ч

Дата

Тип урока

ГЛАВА IV. АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ.

Цель: дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.

15

§9. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ.

Знать:

• понятие последовательности, n-го члена последовательности; арифметическая прогрессия - последовательность особого вида; формулы n-го члена последовательности, арифметической прогрессии; формулы суммы n первых членов для арифметической прогрессии.

Уметь:

• использовать индексные обозначения;

• решать упражнения и задачи, в том числе практического содержания с непосредственным применением изучаемых формул.

7

55

56

Последовательности, п. 24.

СР. ИК. СК.

2

25.01

27.01

УОНМ. Вводная лекция. Практикум.

57

58

Определение арифметической прогрессии. Формула п-го члена арифметической прогрессии, п.25.

МД. СР.

2

29.01

1.02

УОНМ. Обзорная лекция. Исследование. Практикум.

59

60

Формула суммы п первых членов арифметической прогрессии, п.26.

Проверочная СР.

2

3.02

5.02

УОНМ. Исследование. Исторический материал.

61

Обобщающий урок, п.п. 24 - 26.

Тренировочный тест (подготовка к ГИА).

1

8.02

Уроки обобщения, систематизации знаний.

62

Контрольная работа №5 по теме «Арифметическая прогрессия», п.п. 24 - 26.

ФК. ТК. ИК.

1

10.02

Урок контроля и оценки знаний.

§10. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ.

Знать:

• геометрическая прогрессия - последовательность особого вида;

• формулы n-го члена геометрической прогрессии;

• формулы n членов для геометрической прогрессии, для бесконечно убывающей геометрической прогрессии.

Уметь:

• решать упражнения и задачи, в том числе практического содержания с непосредственным применением изучаемых формул.

6

63

64

Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии, п. 27.

Проверочная СР. МД.

2

12.02

15.02

УОНМ. Вводная лекция. Исследова-ние. Практика. УЗИМ. УПЗУ.

65

66

67

Формула суммы п первых членов геометрической прогрессии, п. 28.

СР. МД.

ИК. ВК.

3

17.02

19.02

22.02

УОНМ. Исследова-ние. Практикум. УЗИМ. УПЗУ.

68

Обобщающий урок.

Метод математической индукции, п. 29.

Работа с доп. источниками. Тест (подготовка к ГИА).

1

24.02

Уроки обобщения, систематизации знаний.

69

Контрольная работа №6 по теме «Геометрическая прогрессия», п.п. 27 - 29.

ФК. ТК. ИК.

1

26.02

Урок контроля и оценки знаний.

№

п/п

Раздел, название урока в

поурочном планировании

Требования к уровню подготовки обучающихся

Контроль

знаний

учащихся

Количество

ч.

Дата

Тип урока

ГЛАВА V. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ.

Цель: ознакомить учащихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.

10

§11. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.

Знать:

• понятия: перестановки, размещения, сочетания; относительной частоты, случайного события;

• различные подходы к определению вероятности случайного события;

• формулы для подсчета числа перестановок, размещений, сочетаний.

6

70

Примеры комбинаторных задач, п. 30.

Проверочная СР.

1

29.02

УОНМ. Лекция. Лабораторная работа. УЗИМ. УПЗУ.

71

Перестановки, п. 31.

СР. СК. ИК.

2

2.03

УОНМ. Исследова-ние. Исторический материал. УЗИМ. УПЗУ.

72

Размещения, п. 32.

2

4.03

Усвоение новых знаний в процессе выполнения заданий. УЗИМ. УПЗУ.

73

Сочетания, п. 33.

Уметь:

• решать простейшие комбинаторные задачи на применение изученных формул;

• решать задачи на нахождение вероятностей случайных событий.

СК.

1

7.03

УОНМ. Практикум.

§12. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ.

4

74

Относительная частота случайного события, п. 34.

СР. ВК. ИК.

1

9.03

УОНМ. Вводная лекция.Практика.Исследование.

75

76

Вероятность равновозможных событий, п. 35.

Тест (подготовка к ГИА).

2

11.03

14.03

УОНМ. Частично-поисковая деятельность. Работа с дополнительными источниками.

77

КОНТРОЛЬНАЯ РАБОТА №7 по теме «Элементы комбинаторики и теории вероятностей», п30-36.

Фронтальный письменный контроль.

1

16.03

Урок контроля и оценки знаний

78

79

Обобщающий урок по теме «Элементы комбинаторики и теории вероятностей», п30-36.

Работа с доп. источниками. Тест (подготовка к ГИА).

2

18.03

30.03

Уроки обобщения, систематизации знаний.

№

п/п

Раздел, название урока в

поурочном планировании

Требования к уровню подготовки обучающихся

Контроль

знаний

учащихся

Коли

чество час.

Дата

Тип урока

ИТОГОВОЕ ПОВТОРЕНИЕ.

РЕШЕНИЕ ЗАДАЧ ПО КУРСУ VII - IX КЛАССОВ.

ОСНОВНАЯ ЦЕЛЬ: повторить, закрепить и проверить знания, умения и навыки учащихся по изученному материалу курса алгебра.

26

80

81

82

83

Вычисления.

Знать:

• математические термины и формулы;

• различные методы решения задач, пропорций, уравнений и неравенств, систем уравнений и неравенств;

• графики основных элементарных функций и их свойства;

• способы преобразования выражений.

Уметь:

• правильно употреблять математические термины и формулы;

• применять различные методы при решении задач, пропорций, уравнений и неравенств, систем уравнений и неравенств;

• выполнять преобразование различных выражений.

Решение тренировочных тестовых заданий по сборникам ГИА (подготовка к ГИА)

2

1.04

4.04

6.04

8.04

Уроки обобщения, систематизации знаний.

84

85

86

Тождественные преобразования.

3

11.04

13.04

15.04

Работа с дополнительными источниками информации.

87

88

89

90

Уравнения и системы уравнений.

4

18,20,22,

25.04

Решение тренировочных заданий (подготовка к ГИА)

91

92

93

Неравенства.

3

27.04

29.04

2.05

УЗИМ. УПЗУ.

94

95

96

97

Функции.

3

4,6,11,13.05

УЗИМ. УПЗУ.

98

Итоговая контрольная работа №8.

ФК.

1

16.05

Урок контроля и оценки знаний.

99 - 105

Комплексное повторение основных вопросов курса алгебры.

С Р, тренировочное тестирование. Все виды контроля.

7

18.05-30.05

Уроки практикумы, решение тренировочных тестов (подготовка к ГИА).

32