Урок алгебры 'Решение квадратных уравнений' (8 класс)

Урок алгебры в 8 классе.

Тема: «Решение квадратных уравнений»

Эпиграф к уроку: «Предмет математики настолько серьезен, что полезно не упускать случая, делать его немного занимательным». (Паскаль)

Цель:1) проконтролировать умение решать квадратные уравнения;

2) развивать познавательную и творческую активность учащихся

План урока:

1. Организационный момент «Настроимся на урок».

2. Тест «Квадратные уравнения».

3. Работа по темам: а) математика и биология; б) математика и русский язык.

4. Немного истории: а) квадратные уравнения в Индии; б) квадратные уравнения в Европе.

5. Викторина «Дальше, дальше…»

6. Итог.

Ход урока

1. Организационный момент.

Ученикам сообщаются тема, задачи и план урока. Обращается внимание на эпиграф.

Учитель: Математику не зря называют «царицей наук», ей больше, чем какой-либо науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики - любознательность. Постараемся доказать это на уроке. Вы уже умеете решать квадратные уравнения. Знания не только надо иметь, но и надо уметь их показать, что вы и сделаете на сегодняшнем уроке.

2. Тест «Квадратные уравнения».

Ученики получают карточки.

I вариант.

1). Уравнение вида

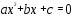, где 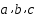- заданные числа, 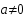, 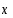- переменная, называется…

2). Полное квадратное уравнение не имеет корней, если D =…

3). Уравнение вида

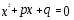- называется…

4). Квадратное уравнение имеет два корня, если …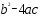

5). Дано уравнение 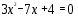. Найти D.

II вариант.

1). Если

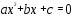, квадратное уравнение, то 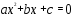… коэффициент, …

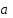2). Уравнени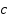е , где 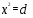<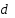имеет…

3). Полное квадратное уравнение имеет единственный корень, если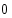

…

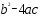4). Уравнение вида , где 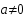, называют…

5). Дано уравнение 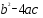. Найти D.

Проводится взаимопроверка. Ответы записаны на доске.

3). Работа по темам.

а) Математика и биология

Учитель: - Даю три определения этому предмету:

1. Непроизводная основа слова.

2. Число, которое после подстановки его в уравнение, обращает уравнение в тождество.

3. Один из основных органов растений.

/Корень/

Учитель: - Вы должны определить, какого растения это корень, решив следующее уравнения.

1.

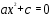
2.

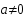
3.

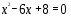
4.

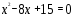
5.

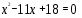
6.

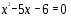
Учитель: - Игра «Математическое лото». Найти карточку со своим ответом и поместить ее в соответствующую ячейку. «Математическое лото» оформляется на магнитной доске. Получается рисунок в виде розы.

Учитель: - Что это за растение?

Ответ: - Роза.

Учитель: - Значит, в черном ящике лежал корень розы, о которой в народе говорят: «Цветы ангельские, а когти дьявольские». О розе существует интересная легенда: по словам Анакреона, родилась роза из белоснежной пены, покрывающей тело Афродиты, когда богиня любви выходила из моря. Поначалу роза была белой, но от капельки крови богини, уколовшейся о шип, стала алой.

Цветы, как люди, на добро

щедры,

И щедро нежность людям

отдавая,

Они цветут, сердца отогревая,

Как маленькие теплые костры.

б) Математика и русский язык

Учитель: - Решите уравнения, корни которых замените буквами, используя соответствие «число буква».

Решив данные номера, вы должны определить, из какого произведения эти строки:

Природа жаждущих степей

Его в день гнева породила,

И зелень мертвую ветвей,

И корни ядом напоила.

1.

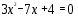
2.

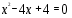
3.

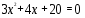
4.

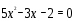
5.

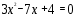
Ключ: наименьший корень - «А» - 1; «Н» - 0,5; «Ч» - 0; «Р» - минус 8.

Ответ: - Корни этих уравнений соответствуют слову «анчар».

Учитель: - Видите, ребята, все в этом мире взаимосвязано: математика, русский язык и литература, биология. Мы увидели, что слово корень, встречается на уроках биологии, русского языка и математики.

4. Немного истории

а) Квадратные уравнения в Индии

Учитель: - По словам математика Лейбница, «кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет».

Задачи на квадратные уравнения встречаются уже в 499 году. В Древней Индии были распространены публичные соревнования в решении трудных задач. Часто они были составлены в стихотворной форме. Вот одна из задач знаменитого индийского математика XII века Бхаскары.

Обезьянок резвых стая,

Всласть поевши, развлекалась

Их в квадрате часть восьмая

На поляне забавлялась.

А 12 по лианам…

Стали прыгать, повисая.

Сколько было обезьянок,

Ты скажи мне, в этой стае?

Ученики решают задачу у доски и в тетрадях.

б) квадратные уравнения в Европе.

Учитель: Формулы решения квадратных уравнений в Европе были впервые написаны в 1202 году. Вывод формулы решения квадратного уравнения встречается у французского математика Ф. Виета.

По праву достойна в стихах быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи, постоянства такого,

Умножишь ты корни - и дробь уж готова.

В числителе С, в знаменателе А.

А сумма корней тоже дроби равна.

Хоть с минусом дробь, что за беда?

В числителе В, в знаменателе А.

Учитель: Как читается теорема Виета?

Ответ

Учитель: Составьте квадратное уравнение, если известны его корни

Х₁=2 , Х₂=-3

Учитель: Сформулируйте теорему, обратную теореме Виета

Ответ

5. Викторина «Дальше, дальше…»

В течение одной минуты ребята отвечают на вопросы, приведенные ниже.

1. Уравнение второй степени.

2. Сколько корней имеет квадратное уравнение, если D больше 0?

3. Произведение корней приведенного квадратного уравнения равно…

4. Равенство с переменной.

5. От чего зависит количество корней квадратного уравнения?

6. Очень плохая оценка знаний.

7. Чему равна сумма корней приведенного квадратного уравнения?

8. Цифровой знак, обозначающий отсутствие величины.

9. Как называется квадратное уравнение, у которого первый коэффициент равен 1?

10. Сколько корней имеет квадратное уравнение, если дискриминант меньше 0?

11.Соперник нолика?

12. Что значит решить уравнение?

13. Есть у любого слова, у растения и может быть у уравнения.

7. Итог урока.

Оценка работы учеников на уроке, домашнее задание.