Конспект урока по математике Различные способы решения уравнений с модулями

МБОУ «СОШ № 20 им. В. Митты с углубленным изучением отдельных предметов»

Урок математики для 8 класса

(углубленное изучение математики)

по теме « Различные способы решения

уравнений с модулями».

.

Учитель математики: Судеркина Маргарита Владимировна

МБОУ «СОШ № 20 им. В. Митты с углубленным изучением отдельных предметов»

г.Новочебоксарск Чувашской Республики.

План урока:

1. Вступительное слово учителя.

2. Повторение ранее изученного.

1.Фронтальный опрос.

2. Математический диктант с последовательной проверкой.

3.Индивидуальная работа с последовательной проверкой.

3. Физкультминутка.

4. Изучение новой темы.

5. Закрепление изученного. Работа по вариантам.

6. Решение уравнений, сводящихся к уравнениям с модулями. ГИА 2010.

7. Подведение итогов.

8. Домашняя работа.

Цели и задачи:

1. Отработать навыки решений уравнений с модулем;

2. Рассмотреть некоторые новые методы решения уравнений с модулем;

3. Развивать внимательность, логическое мышление, самостоятельность и творческий подход к решению уравнений с модулем.

«Знание - самое превосходное из владений.

Все стремятся к нему,

само же оно не приходит».

Ал - Бируни

Задания, содержащие модуль-это один из самых трудных материалов, с которыми школьники сталкиваются на экзаменах.

Задачи, связанные с абсолютными величинами, часто встречаются и на математических олимпиадах. Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсе высшей математики.

II. Повторение изученного.

1. Блиц-опрос.

   • Определение уравнения с одной переменной?

   • Что такое корень уравнения?

   • Что значит решить уравнение?

   • Какие уравнения называются уравнениями с модулем?

2. Математический диктант с последующей проверкой. Выставление оценок.

   • Модуль числа х - это расстояние от

начала координат до точки, выраженное

в единичных отрезках.

• Модуль любого числа положителен.

• Модуль положительного числа всегда

положителен.

• Модуль отрицательного числа

всегда отрицателен.

• Модуль отрицательного числа

иногда положителен, иногда

отрицателен.

• Модуль отрицательного числа всегда

положителен

• Модуль О всегда равен О.

• Модуль О всегда положителен.

• Модуль любого числа всегда равен

числу, противоположному данному

• Модуль отрицательного числа

всегда равен числу, противопо-

ложному данному отрицательному

числу.

• Если |х|= 17, то х = 17.

• Если | -х | =27, то х = 27.

• Если |с | = -12, то с = 12.

  3. Индивидуальная работа. Работа у доски.

Решить уравнения:

• ||2х-1|-4|=6 метод последовательного раскрытия скобок.

Ответ: 5,5; -4,5.

Рассмотрим два случая.

1) Исходя из определения модуля, произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то уравнение примет вид :

|2х-1|-4=6, |2х-1|=10. Используя еще раз определение модуля, получим: 2х-1=10 либо

2х-1= -10. Откуда х1=5,5;х2= -4,5

2)Если значение выражения под знаком модуля отрицательно, то по определению имеем уравнение

|2х-1|-4= -6, |2х-1|= -2. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен.

Ответ: 5,5; -4,5.

• │x - 1│- 2 │x + 2│= 0 методом интервалов.

Найдем точки перемены знака модуля из условий:

х - 1 = 0 и х + 2 = 0

х = 1 х = - 2

Рассмотрим данное уравнение

на промежутках

(- ∞;-2], [-2;1] , [1;+∞)

На промежутке (- ∞; -2 ]

│ х - 1 │ = - х + 1 ; │ х + 2 │ = - х - 2

значит, уравнение имеет вид:

( - х + 1 ) - 2∙ (- х - 2) = 0

- х + 1 +2х + 4 = 0

х + 5 = 0

х = - 5

- 5 принадлежит (- ∞; -2 ]

На промежутке [-2;1]

│ х - 1 │ = - х + 1; │ х + 2 │ = х + 2

значит, уравнение имеет вид:

( - х + 1 ) - 2∙ ( х + 2) = 0

- х + 1- 2х - 4 = 0

- 3х - 3 = 0

3х = - 3

х = - 1

- 1 принадлежит промежутку [-2;1]

На промежутке [1;+∞)

│ х - 1 │ = х - 1; │ х + 2 │ = х + 2

значит, уравнение имеет вид:

( х - 1 ) - 2∙ ( х + 2) = 0

х - 1 - 2х - 4 = 0

- х - 5 = 0

х = - 5

- 5 не принадлежит [1;+∞)

Ответ: -5;-1.

• │x - 1│- 2 │x + 2│= 0 графический способ.

Построим график функции у = │x - 1│- 2 │x + 2│

Найдем точки перемены знака модуля из условий:

х - 1 = 0 и х + 2 = 0

х = 1 х = - 2

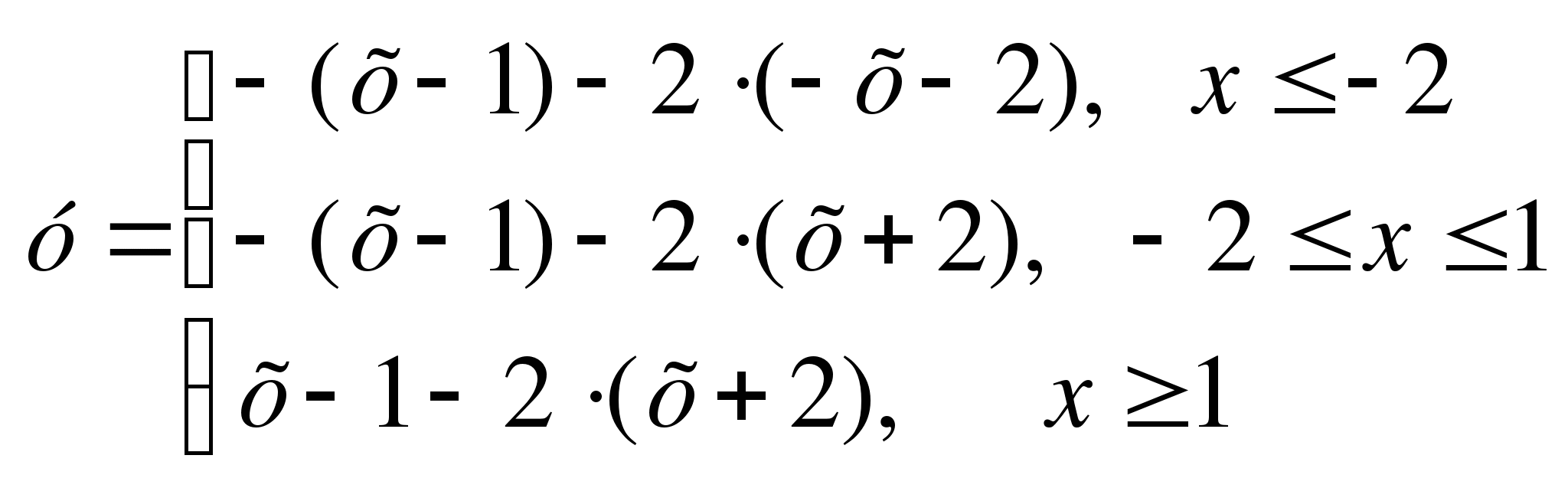
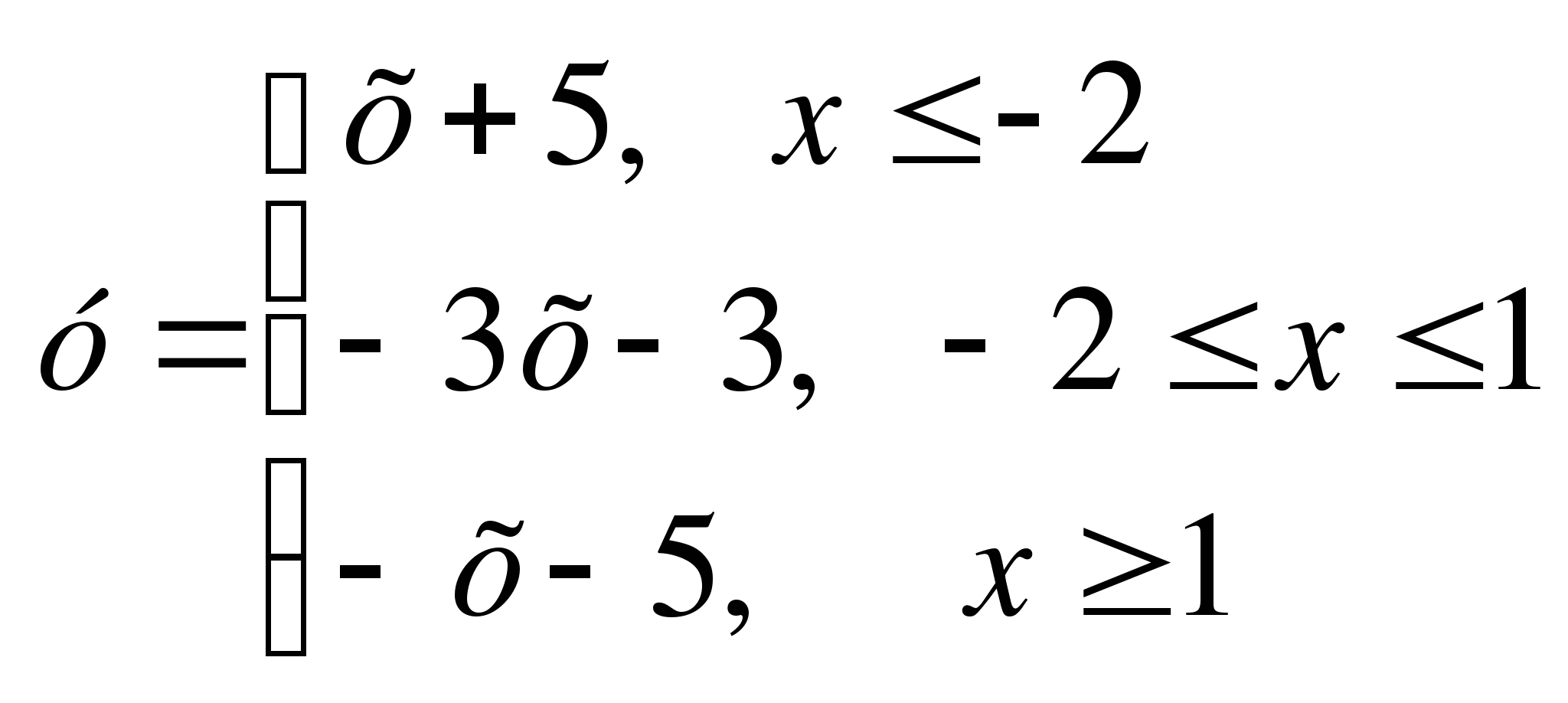
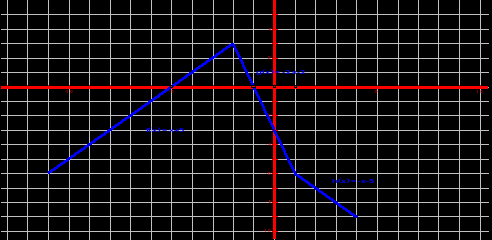
Ответ: -5;-1

III. Физкультминутка.

IV. Изучение новой темы.

1.Основные способы решения уравнений с модулями:

• Метод последовательного раскрытия модуля.

• Раскрытие модуля на интервалах.

• «Сравнение модулей»

• «Сравнение квадратов»

• Графический способ.

2. Опорная информация. Свойства модуля, на котором основаны способы «Сравнение модулей»,

«Сравнение квадратов»:

• |а|²=а²

• Если |а|=|в|, то а=в или а=-в;

• Если а²=в² , то а=в или а=-в;

• Если |а|=|в|, то а²=в²

• |cx|=c|x|, c-неотриц.

3.Решение уравнения │x - 1│- 2 │x + 2│= 0

«Сравнение модулей»,

│x - 1│= 2 │x + 2│

│x - 1│= │2x + 4│

Модули равны у чисел равных или противоположных

х - 1 = 2х + 4 или х - 1 = - 2х - 4

- х = 5 3х = - 3

х = - 5 х = - 1

Ответ:-5,-1

«Сравнение квадратов»

│x - 1│= 2 │x + 2│

Учитывая, что если |а|=|в|, то а²=в²

Получим:

(x - 1) ² = (2 (x + 2)) ²

используем формулы квадратов суммы и разности двучлена

х²- 2х + 1 = 4 ∙ (х² + 4х + 4)

х²- 2х + 1 = 4х² + 16х + 16

3х² + 18х + 15=0

х² + 6х + 5=0

по теореме, обратной теореме Виета, найдем корни

х = - 5 х = - 1 Ответ: -5,-1

V. Закрепление изученного.

Решите уравнения:

Вариант1

Сравнение модулей

|х²-8х+5|=|х²-5|

Решение:

Учитывая соотношение( если |а|=|в|, то а=в или а=-в), получим:

х²-8х+5=х²-5 или х²-8х+5=-х²+5

х=1,25 х=0 или х=4.

Ответ: 1,25; 0; 4.

Вариант2

Сравнение квадратов

|х+3|=|х-5|.

Решение:

В силу соотношения (если |а|=|в|, то а²=в²) получаем:

(х+3)²=(х-5)²;

х²+6х+9= х²-10х+25;

х=1.

Ответ:1.

VI. Решение уравнений, сводящихся к уравнениям с модулями.

1.

Р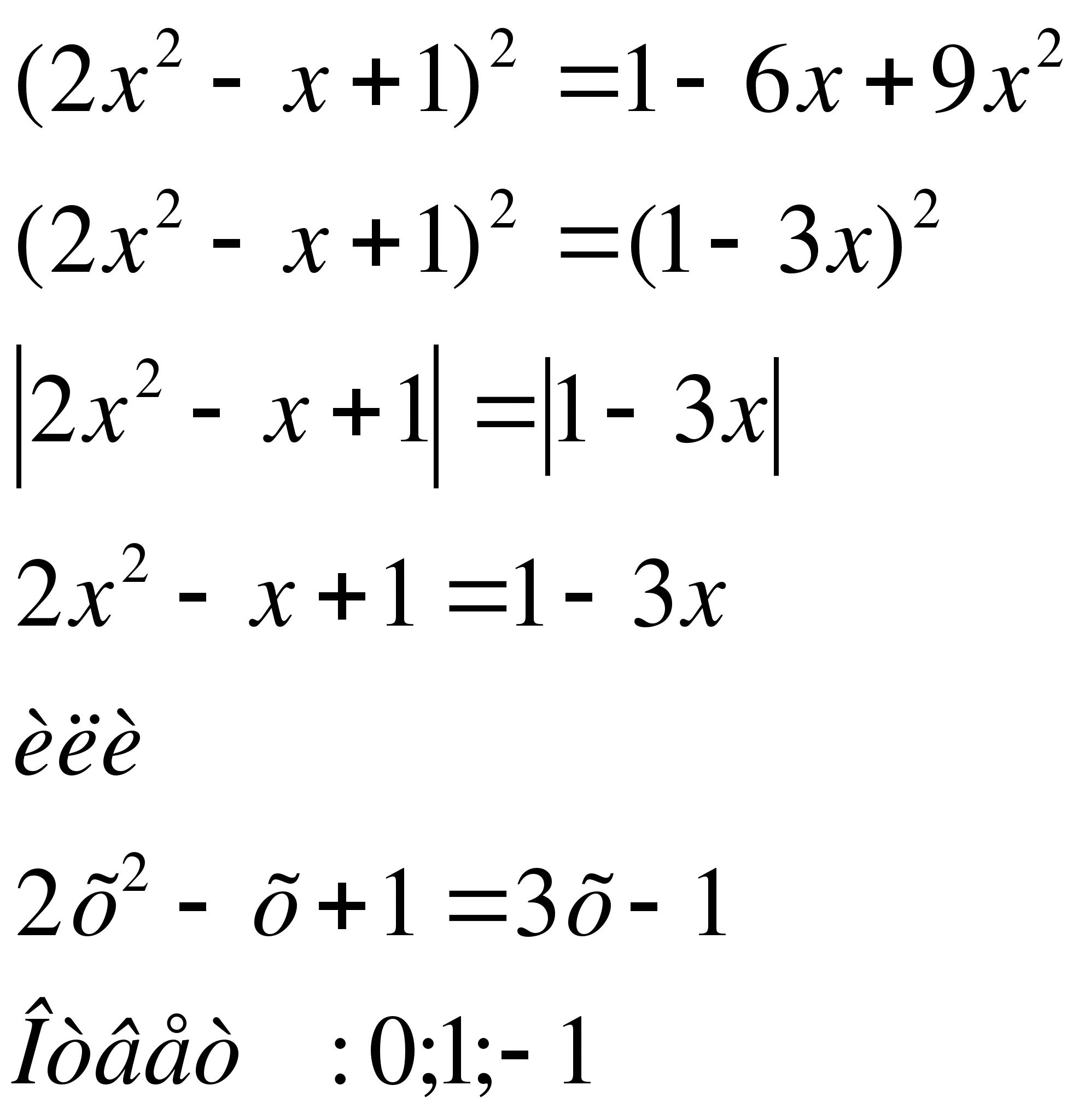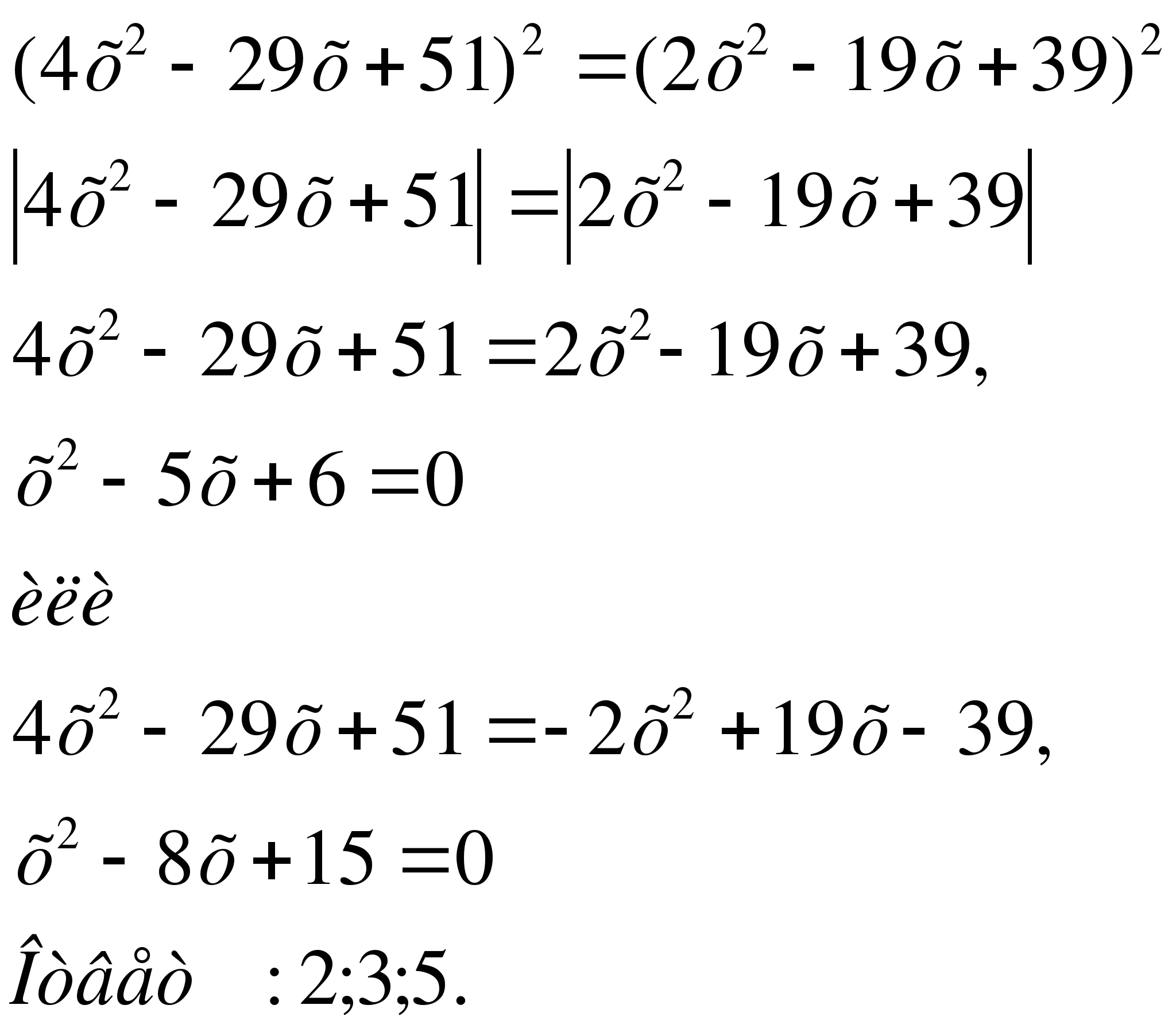ешение:

2. Решите уравнение.

Решение:

VI. Подведение итогов

.