Урок - лабораторная работа 8 класс «Свойства коэффициентов квадратного уравнения»

Острянина Ирина Витальевна

учитель математики первой категории

Новоишимской СШ №2

Района имени Габита Мусрепова

Северо-Казахстанской области.

Алгебра 8 класс

Тип урока: лабораторная работа

Тема: Решение квадратных уравнений. (Урок является последним в теме «Решение квадратных уравнений по формулам корней», теорему Виета учащиеся будут изучать на следующем уроке).

Цели урока:

1. Выявление свойств коэффициентов квадратного уравнения.

2. Использование выявленных свойств при решении квадратных уравнений.

3. Решение квадратного уравнения с помощью циркуля и линейки.

Задачи урока: обучающие и развивающие:

1. Проанализировать влияние коэффициентов на решение квадратного уравнения.

2. Исследовать сумму коэффициентов квадратного уравнения, закономерностей корней.

3. Исследовать влияние коэффициентов на знаки корней квадратного уравнения.

4. Нахождение корней квадратного уравнения с помощью циркуля и линейки.

5. Развивать логическое мышление, математическую речь, мышление, память.

Воспитательные:

1. Воспитывать творческую личность, прививать интерес к предмету, к исследовательской деятельности.

Раздаточный материал: ход лабораторной работы, набор уравнений, задания ВОУД.

ХОД УРОКА:

I этап: Актуализация

Вступление учителя:

При решении текстовых задач с несколькими неизвестными используется алгебраический метод решения, т.е. составление и решение уравнений. Многие задачи приводят к квадратным уравнениям. Квадратные уравнения умели решать около 2000 лет до нашей эры. Современные обозначения и решение квадратных уравнений были найдены в трудах Леонардо Фибоначчи, Михаила Штифеля, Рене Декарта, Исаака Ньютона и Франсуа Виета.

Решение квадратных уравнений по формулам связано с вычислениями выражений, зависящих только от значений коэффициентов квадратного уравнения; с помощью теоремы Виета корни квадратного уравнения могут быть найдены подбором, могут быть определены знаки корней, но многие свойства коэффициентов не отражены в школьных учебниках математики, а зная их, можно экономить время и эффективно решать уравнения.

II этап: Анализ домашней работы: Наибольшее число ошибок допускается при нахождении дискриминанта, а именно в произведении 4ас неверно определяется знак «-» или «+».

Повторим материал 6 класса: если в произведении чётное число отрицательных множителей, то ставится знак «+», если в произведении нечётное число отрицательных множителей, то ставится знак «-». Примечание: число 4 формуле имеет знак «-».

D = b- 4ас.

Дискриминант квадратного уравнения ax² + bx + c = 0

Проверим: Решим: (устно)

D = 4- 45(-1)= 16+20=36

D = (-2)- 416(-5)= 4+320=324

D = (-36)- 42811= 1296 - 1232= 64

D = 21- 4(-49)(-2)= 441-392=49

D=(-3)- 4(-2)(-1) =

D= 6- 491=

D=1- 4(-20)1=

III этап: лабораторная работа

Тема: Решение квадратных уравнений.

Цель: исследование свойств коэффициентов квадратного уравнения; существования наличия связей между коэффициентами квадратного уравнения, которые помогут более эффективно и экономично решать его.

Практическое нахождение корней уравнения с помощью циркуля и линейки.

Оборудование: набор квадратных уравнений, циркуль, линейка, карандаш.

Объект исследования: квадратные уравнения.

Ход работы:

I этап

Некоторые свойства коэффициентов квадратного уравнения.

1. Если а и с имеют противоположные знаки, то уравнение имеет действительные корни. А именно:

Если с - положительное число корни имеют одинаковые знаки (в <0, то корни положительные; в>0, то корни отрицательные).

Если с - отрицательное число корни имеют противоположные знаки ( в>0, то корень больший по модулю отрицательный).

Выполнить задание: тесты ВОУД

2.

Если а + в + с = 0 , то х=1, х=.

Пример. Рассмотрим уравнение х² +4х - 5= 0.

а+ b+c= 0, х=1, х=. 1+ 4+(-5)= 0.

Значит корнями этого уравнения являются 1 и -5. Проверим это с помощью нахождения дискриминанта:

D= b- 4ас= 4- 4∙1∙(-5)= 36.

х=== - 5.

х===1.

3.

Если а + с = в, то х= -1, х=

Пример. Рассмотрим уравнение 2х² +8х +6 = 0.

Если b= а+c, то х= -1, х=. 8 =2 +6.

Значит корнями этого уравнения являются -1 и -3. Проверим это с помощью нахождения дискриминанта:

D= b- 4ас=8- 4∙2∙6= 16.

х=== -3.

х=== -1.

4. Закономерность коэффициентов:

1) Если в уравнении ax² + bx + c = 0 коэффициент b равен (а² +1), а коэффициент с численно равен коэффициенту а, то его корни равны

х= -а; х= -.

Пример. Рассмотрим уравнение 6х² +37х +6 = 0.

х= -6; х= -.

2) Если в уравнении ax² - bx + c = 0 коэффициент b равен (а² + 1), а коэффициент с численно равен коэффициенту а, то его корни равны

х= а; х= .

Пример. Рассмотрим уравнение 15х² -226х +15 = 0.

х= 15; х= -.

3) Если в уравнении ax² + bx - c = 0 коэффициент b равен (а² - 1), а коэффициент с численно равен коэффициенту а, то его корни равны

х= -а; х= .

Пример. Рассмотрим уравнение 17х² +288х - 17 = 0.

х= -17; х=.

4) Если в уравнении ax² - bx - c = 0 коэффициент b равен (а² - 1), а коэффициент с численно равен коэффициенту а, то его корни равны

х= а; х= -.

Пример. Рассмотрим уравнение 10х²-99 х - 10 = 0. х= 10; х= -.

II этап

Решение квадратных уравнений с помощью циркуля и линейки

Графический метод решения квадратных уравнений имеет существенные недостатки: он достаточно трудоёмкий, при этом точность построения кривых - парабол низка.

Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.

Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.

1. Построить в системе координат Oxy окружность с центром в точке 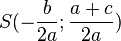, пересекающую ось y в точке C(0;1).

2. Абсциссы точек пересечения окружности с осью Ох - корни уравнения.

Возможны три случая:

• длина радиуса окружности превышает длину перпендикуляра к оси абсцисс, опущенного из точки S: в этом случае окружность пересекает ось x в двух точках, а уравнение имеет два действительных корня, равных абсциссам этих точек;

• радиус равен перпендикуляру: одна точка и один вещественный корень кратности 2;

• радиус меньше перпендикуляра: корней в множестве 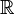нет.

Задание №121(3,4)

Вывод:_______________________________________________________________________________________________________________________________________________

Оценка: в течение урока по ходу решения уравнений: по тексту лабораторной работы, из набора, а также за задания ВОУД учащиеся получают карточки (см. приложения) и в конце урока каждый находит среднее арифметическое своих оценок.

Домашнее заданние:

1. Теоритический материал. х2 + рх + q = 0,

Рассмотреть приведённое квадратное уравнение, где р и q - любые числа отличные от нуля.

Если свободный член q приведённого квадратного уравнения положителен ( q > 0 ), то уравнение имеет два одинаковых по знаку корня

и это зависит от второго коэффициента р. Если р > 0 , то оба корня отрицательны ,

если р < 0 , то оба корня положительны.

ПРИМЕР:

х - 14х + 48 = 0 х + 19х + 90 = 0

х= 6 , х =8 , х= -9 , х =-10

ОТВЕТ : 6; 8 ОТВЕТ : - 9 ; - 10

Если свободный член q приведённого квадратного уравнения отрицателен ( q < 0 ), то уравнение имеет два различных по знаку корня,

причём больший по модулю корень будет положителен, если р < 0,

если р > 0 - отрицателен.

х - 2х - 15 = 0 х + 2х - 8 = 0

х= 5 , х =-3 х=-4 , х =2

ОТВЕТ : 5 ; -3 . ОТВЕТ : - 4 ; 2.

2. Решить квадратные урвнения с помощью циркуля и линейки

№121 (1,2) учебник для 8 класса «Алгебра» /А. Абылкасымова, И. Бекбоев , А. Абдиев, З. Жумагулова/.

3. Решить квадратные уравнения с использованием свойств коэффициентов :

№129(1,4)

ПРИЛОЖЕНИЯ

ВОУД (задания из сборника тестов):

Не решая уравнений, укажите, какие из них имеют корни с противоположными знаками:

Задание 1:

х- x - 6=0

х-5x + 6=0

х- x - 12=0

х- 8x + 15=0

х- 2x - 15=0

А. 1,2,3

В. все

С. 1,3,5

Д. 4,2,3

Е. 2,3,4,5

Задание 2:

х- 3x - 54=0

х+ x - 12=0

2х+ 7 x + 3=0

5х+ 4x - 1=0

3х- 5x - 2=0

А. 1,3,5

В. 1,2,3

С. 1,2,4,5

Д. все

Е. 3,4,5

Задание 3:

2х+ 5x - 3=0

3х+ 5x - 3=0

4х+ 13x + 3=0

х- 11x + 30=0

х+ 15x + 54=0

А. 1,3,5

В. 1,2,5

С. 1,2

Д. все

Е.4,5

Задание 4:

х- 4,5x + 2=0

3х+8x -3=0

3х+ 7x - 3=0

х- 7x + 10=0

х- 3x - 18=0

А. 1,2,3

В. 2,3,5

С. 3,4,5

Д. 1,5

Е. все

Задание 5:

х- x - 20=0

5х-26x + 3=0

х+ 10 x + 9=0

х- 4x + 3=0

х- 2x - 3=0

А. 1,2,5

В. 1,3,5

С. 1,5

Д. 3,4,5

Е. все

ФИ____________________________________

Ответы:

Задание 1:

Задание 2:

Задание 3:

Задание 4:

Задание 5:

Ответы:

Задание 1: С. 1,3,5

Задание 2: С. 1,2,4,5

Задание 3: С. 1,2

Задание 4: В. 2,3,5

Задание 5: С. 1,5

Набор уравнений:

Свойства коэффициентов квадратного уравнения:

I. №128(4), №133 (4)

а) 4х² - 12х +8х = 0.

б) х² - 6х + 5= 0.

в) 45х² - 23х - 22= 0

г) х² + 6х - 7= 0

д) 11 х² + 25х - 36= 0.

е) 3х² + 5х - 8= 0

ж) 5 х² - 7х + 2= 0

з) 5х² + 4х - 9= 0

и) 2х² + 3х + 1= 0

к) х² + 17х - 18= 0

л) 345х² - 137х - 208= 0.