Урок математики в 9 классе по теме

Тема: "Арифметическая и геометрическая прогрессии"(9 класс)

Цель:

• закрепить знания учащихся по теме «Прогрессии»

• формировать навыки работы с формулами

• отработать определения

• совершенствовать навыки счета

• расширять кругозор учащихся

• развивать логическое мышление, математическую речь уч-ся.

Ход урока:

1). Организационный момент. На последних уроках алгебры мы говорили с вами об арифметической и геометрической прогрессиях Сегодня мы ознакомимся с историей возникновения прогрессии и обобщим наши знания по изученной теме и решим задачи повышенной сложности.

2). Историческая справка о прогрессиях.

3). Итак, вы услышали, что прогрессии возникли в глубокой древности из практических нужд человека. Решим одну из древнейших задач на прогрессии из древнеегипетского папируса.

Задача Ахмеса: (мультимедийный проектор)

4) Для решения задачи мы воспользовались определением арифметической прогрессии, рекуррентной формулой арифметической прогрессии и формулой суммы n первых членов арифметической прогрессии. Сформулируем определение арифметической прогрессии и геометрической прогрессии, вспомним свойство среднего члена прогрессии и решим задачу, связывающую обе эти прогрессии. (для сильных)

5) Задача. (из сборника Сканави №4.044) Найдите четыре числа, первые три из которых составляют геометрическую прогрессию, а последние три - арифметическую прогрессию. Сумма крайних чисел равна 21, а сумма средних 18.

6) Одновременно с задачей из Сканави для слабоуспевающих учащихся индивидуальные карточки.

7) Математический диктант или устные упражнения.

8) Когда известному немецкому математику 19 века Карлу Фридриху Гауссу было 9 лет, учитель на уроке математики предложил детям задачу: «Найдите сумму первых членов натурального ряда чисел.» Гаусс решил задачу в течение 1 мин. Сумеете ли вы также быстро решить ее?

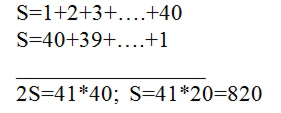
Резюме: Таким образом мы убедились, что прогрессии возникли в глубокой древности из практических нужд человека. Изучаются в школе как частные случаи последовательностей. Решение задач повышенной сложности, потребовало от нас: знание определений, формул, навыков счета в обыкновенных и десятичных дробях.