Урок + презентация по математике для 11 класса по теме «Решение логарифмических уравнений. Нестандартные приёмы решения»

ГОУ НПО « Куртамышское ПУ-интернат»

Проект урока

Тема: «Решение логарифмических уравнений. Нестандартные приёмы решения»

Преподаватель: Умнова Е.Ф.

Подробный конспект урока.

Организационная информация

Тема урока

«Решение логарифмических уравнений. Нестандартные приёмы решения»

Предмет

Алгебра и начала анализа

Курс

1

Автор урока (ФИО, должность)

Умнова Елена Фёдоровна математики

Образовательное учреждение

ГОУ НПО « Куртамышское ПУ - интернат

Республика/край, город/поселение

Курганская область

Методическая информация

Тип урока

Обобщающий

Цели урока

Образовательные: Отработать умения систематизировать, обобщать свойства логарифмической функции, применять их при решении логарифмических уравнений, применять различные методы решения логарифмических уравнений.

Развивающие: Использовать ранее усвоенные знания и переносить их в новую ситуацию, развивать у обучающихся мыслительные операции, анализ, классификацию, внимание, математическую речь.

Воспитательные: Создать эмоционально-положительный комфорт( ситуацию успеха)

Задачи урока

Ранее усвоенные знания, применять в нестандартных ситуациях.

Знания, умения, навыки и качества, которые актуализируют, закрепят ученики в ходе урока

-знание понятия логарифма числа, логарифмической функции, свойств логарифмической функции;

-знание основных приёмов решения логарифмических уравнений;

- знание квадратичной функции и её свойств;

-умение выполнять преобразования выражений, содержащих логарифмы;

-умение применять свойства логарифмов при преобразовании выражений, содержащих логарифмы;

-умение решать простейшие логарифмические уравнения и применение основных приёмов при решении более сложных уравнений;

- умение решать квадратные уравнения;

-умение находить область значений функции.

Необходимое оборудование и материалы

Компьютер, проектор, экран.

Ход урока и содержание урока:

1.Орг.момент

2.Тренинг. Устная работа. Найди ошибки. Повторить основные формулы логарифмов.

3.Программируемый контроль.

4.Постановочно-практическое задание.

5.Решение проблемной ситуации.

6.Выводы. Домашнее задание.

7..Итог урока

8. Рефлексия («Что знают», «Чего не знают», «Что получилось?», «Что нет»).

1.Орг.момент.

На перемене обучающиеся на списке уравнений, которые были заданы как

домашнее задание ставят «+» против тех уравнений, которые дома не вызвали затруднений.

Домашнее задание: Самопроверка по эталону.

№ 516 в)

г)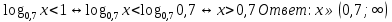

№ 517 в)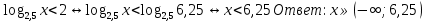

Ответ: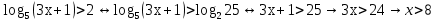

Г)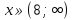

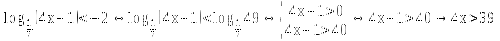
2.Тренинг. Устная работа

Динамичные блоки уравнений (презентация)

В ходе этой работы систематизируются знания обучающихся по свойствам логарифмической функции, основные методы решения логарифмических уравнений, предложенных в учебнике.

I блок. На слайде записаны формулы. Определить, какие из них записаны неверно.

( слайд)

Проверить методом самоконтроля.

Итог повторения . Слайды4-9.

3. Программированный контроль.

Проверить методом взаимоконтроля используя слайд 10

Программируемый контроль.

Задание

Ответ

Вариант 1

Вариант 2

1

2

3

4

1.Найти область определения логарифмической функции

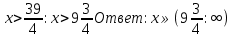
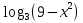
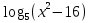
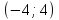
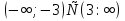
(-3:3)

2. Решить логарифмическое уравнение

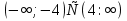
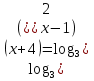
-7

5

1

0

3. Решить логарифмическое неравенство

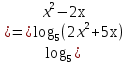
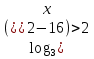
(-5;5)

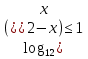
(1;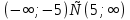

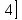
Физкультминутка.

3.Постановочно-практическое задание.

Какие вы знаете методы решения логарифмических уравнений и неравенств? Слайд 11.

Работа в парах. Разобрать примеры решений логарифмических уравнений, определить метод решения уравнений, объяснить решение примеров товарищу.

В лист самоучёта ставит оценку за объяснение тот кому объясняют решение.

Анализируем, какие уравнения не вызвали сложности, а какие вызвали.

Какое из уравнений отличное от остальных? ( слайд)

1. log₉(x-1)²=1

2. ln(x²-15)=ln x

3. log₂(x²-3x-10)=3

4. log₃x=2log₃ 9- log₃ 27

5. ln(x-5)=0

6. log₂ log₃ log₄ x=0

. О чём говорит этот блок уравнений? Определите метод решения уравнений.

( слайд)

1. log_ax=2log_a3+log_a5

2. lg(x-9)+lg(2x+1)=2

3. log₅(x²+8)-log₅(x+1)=3log₅2

4. 1/2log₂(x-4)+1/2log₂(2x-1)=log₂3

О чём говорит этот блок? Каким методом необходимо решать уравнения этого блока (слайд)

1. log²₂(x+8)-6 log₂(x+8)=-5

2. log²₂x-log₂x=2

3. lg²x-lgx²+1=0

4. log_x2- log₄x+7/6=0

5. log_x+1(2x²+5x-3)=2

6. lg100x*lgx=-1

После устной работы с классом анализируется и проверяется работа обучающихся на доске

4.Решение проблемной ситуации.

Разбираем решение уравнений, которые у большинства обучающихся вызвали затруднения. Если есть обучающиеся, которые их решили, то они представляют своё решение.

У учителя все уравнения с решениями в презентации и при необходимости уравнение разбирается по готовому решению или проверяется ответ.

5

2

5

1.x^{lg x+lgx -12} =10^2lgx

2

5

ОДЗ: х>0

(lg²x+5lgx-12)lgx=2lgx

lgx(lg²x-5lgx-14)=0

x=1 a²-5a-14=0

Ответ: х=10⁷ ;х=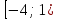

2.(x+1)×log₃x+4xlog₃x+16=0

a=x+1 b=4x c=-16

log₃x=t

(x+1)t²+4xt-16=0

D=16t²+64x+64=(4x+8)²

t₁= 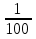= = 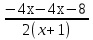-4

t₂= =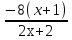

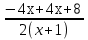
log₃x= -4 log₃x= 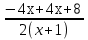Решим графически, построим функции у= log₃x и у=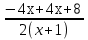

x = 3^-4 При построении получаем общую точку х=3

x =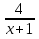

Ответ: 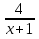; 3.

3. log₂(4x-x²)=x²-4x+6 ОДЗ: 4x-x²>0

Рассмотрим функции: x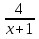(0;4)

y= log₂(4x-x²) и y= x²-4x+6

Определим области значений данных функций:

y= x²-4x+6 -это квадратичная функция, графиком функции является парабола и область значений зависит от вершины параболы. Координаты вершины (2;2) Значит область значений данной функции y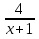

y= log₂(4x-x²) , пусть t=4x-x² -это квадратичная функция, графиком функции является парабола и область значений зависит от вершины параболы. Координаты вершины (2;4),

t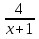 (-;4] ; y= log₂ t -возрастающая функция и своё максимальное значение принимает при максимальном значении t, т.е. при t=4 log₂ 4=2

log₂(4x-x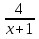²) (-;2]

Значит общее решение будет при log₂(4x-x²) =2 и x²-4x+6 =2

log₂(4x-x²) =2 x²-4x+6 =2

4x-x² =4 x²-4x +4=0

х=2 х=2

Ответ:х=2

5. Итог урока.

Что нового узнали сегодня на уроке? Какие новые методы решений логарифмических уравнений сегодня разобрали.(Метод оценки, квадратное относительно разных переменных, разложение на множители, логарифмирование)

Домашнее задание:тест, Творческое задание: реферат на тему из истории логарифмов.

6. Этап рефлексии.

Напишите письмо другу об уроке, дайте поставьте себе оценку за урок.

Лист самоучёта

Ф.И. учащегося

Д.З

П.Ф.

П.К

Р.П..

Р.П.С.

Э.Р.

Оценка