- Учителю
- Исследовательская работа 'Теорема о четырех красках' (6 класс)
Исследовательская работа 'Теорема о четырех красках' (6 класс)

Муниципальное автономное общеобразовательное учреждение
«Основная общеобразовательная школа № 32»
Теорема о четырех красках
(материалы на IV городскую научно-практическую конференцию
школьников по математике «Шаги в науку»)
Автор:
Иванова В.В.,
обучающаяся 6 класса
Руководитель:
Степанова О.В.
учитель математики
Анжеро-Судженск 2015
Содержание
I
Введение
3
II
Проблема четырех красок
2.1. История возникновения теоремы
6
2.2. Игра четыре краски
10
2.3. Тематические задачи
12
III
Заключение
14
Литература
16
Приложение
17
-
Введение
Исследовательская работа посвящена изучению «Теоремы о четырех красках». Цель проекта - понять, и изучить теорему о четырёх красках.
Задачи работы:
1.Изучить имеющуюся литературу по данной теме.
2.Провести исследование по данной теме.
3.Рассказать о теореме четырёх красок.
4.Проверить данную теорему на практике.
К задачам хотелось бы отнести: обзор истории изучения данной теоремы, поиск практического применения ее не только в математике, но и в других научных дисциплинах, например, в географии. К методам исследования относятся поисковый, исторический, картографический и другие.
Работа состоит из введения, основной части, заключения, списка и спользованной литературы и приложения.
Многие люди путаются в непонятных математических символах и строгих математических правилах, всегда избегая решения тех проблем, в которых встречаются не только буквы, но и цифры. Безусловно, математика бывает очень сложной, но те результаты, которые можно с помощью нее получить, могут быть достаточно неожиданны, красивы и просто поразительны.

Теорема Брауэра о неподвижной точки
Это теорема из такого раздела математики как топология, была доказана Лёйтзеном Брауэром. Ее чисто математическое выражение является достаточно абстрактным, но ее можно неожиданным способом применить к разным реальным событиям. Допустим, что у нас есть какая-нибудь картина (к примеру Мона Лиза), и мы можем сделать ее копию. Потом мы можем делать с этой копией что захотим - увеличивать, уменьшать, вращать, сминать, все что угодно. Терема Брауэра о неподвижной точке гласит, что если эту деформированную копию положить на оригинал, то всегда найдется хотя бы одна точка на копии, которая будет находиться ровно над этой же самой точкой изображения на оригинале. Это может быть кусочек уха, рта или глаза Моны, но обязательно такая точка найдется.
Теорема работает и в трехмерном пространстве. Представьте, что у нас есть стакан воды, в который мы положили ложку и размешивали воду столько, сколько захотим. По теореме Брауэра, всегда будет хотя бы одна молекула воды, которая в итоге окажется ровно на том же самом месте, что и до размешивания.
Парадокс Рассела
На рубеже 20-го века многие ученые были увлечены новым разделом математики - теорией множеств. В принципе, множество - это совокупность каких-либо объектов. В те времена, считалось, что любой набор объектов можно считать множеством - множество всех фруктов, множество всех президентов США, и все это считалось верным. Стоит добавить, что одно множество может включать в себя другие множества. В 1901 году известный математик Бертран Рассел сделал нашумевшее открытие, когда понял, что такой способ мышления ошибочен - на самом деле не все совокупности объектов можно назвать множеством.
Решив разобраться в этом вопросе, Рассел описал множество всех множеств, которые не содержат себя в качестве своих элементов. Множество всех фруктов не содержит в себе само себя, так что его можно включить во множество Рассела, как и огромное количество других множеств. Но что насчет самого множества Рассела? Оно не содержит в себе само себя, так что его тоже надо включить в это множество. Погодите ка… теперь оно содержит себя в самом себе, так что нам нужно его исключить. Но теперь его нужно включить в себя снова, так как на этот момент, оно не содержит себя в самом себе. Ну и так далее. Этот логический парадокс привел к пересмотру теории множеств, одному из самых важных направлений в современной математике.

Великая теорема Ферма
Самая известная теорема Пьера Ферма говорит о том, что это выражение x2 + y2 = z2 не имеет натуральных решений x, y и z, если в степенях находится любое натуральное число больше двух.
Как писал сам Ферма: «…невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него». Проблема в том, что Ферма написал это в 1637 году, а недоказанной она оставалась еще долгие годы. И только в 1995 году (спустя 358 лет) теорема была доказана Эндрю Уайлсом.
Теорема о конце света
Математика может быть использована для определения того, когда наш вид полностью вымрет. Используя вероятности, но тем не менее.
Это теорема (которая существует уже примерно 30 лет и была открыта и переоткрыта уже несколько раз) говорит о том, что время человечества уже на исходе. Одно из доказательств (которые принадлежит астрофизику Ричарду Готту) на удивление простое: если рассматривать все время существования человеческого вида как процесс жизни отдельного организма, то можно определить на каком этапе жизни наш вид находится.
Согласно Готту, человечество вымрет в интервале от 5100 лет до 7,8 миллионов лет от текущего времени. Итак, человечество, тебе пора писать завещание.
В середине ХIX столетия возникло совершенно новое течение в геометрии, которому было суждено вслед за тем стать одной из главных движущих сил современной математики. Предметом новой отрасли, называемой топологией (или analysis situs), является изучение свойств геометрических фигур, сохраняющихся даже тогда, когда эти фигуры подвергаются таким преобразованиям, которые уничтожают все их и метрические и проективные свойства.

Тополог интересуется теми свойствами «предметов» (трактуемых нами пока в геометрическом смысле), которые наиболее устойчивы, то есть которые выдерживают деформации сжатия и растяжения.
Все это может навести на мысль, что топология занимается придумыванием строгих доказательств для таких истин, в которых не станет сомневаться ни один здравомыслящий человек. Но это совсем не так: существует много вопросов топологического характера, в числе которых иные формулируются чрезвычайно просто и на которые интуиция не дает удовлетворительных ответов. Примером может служить знаменитая "проблема четырех красок".
-
Проблема четырех красок
2.1.История возникновения теоремы
С тех пор, как появились первые географические карты, встал и вопрос о том, как их лучше всего раскрашивать. С одной стороны, каждая отличная от прочих территория должна быть окрашена в свой цвет. С другой стороны, строгая функциональность не допускала кричащей пестроты. Да и типографские возможности тех времен были не так уж велики. В связи с этим, географы поставили перед математиками задачу, на первый взгляд казавшуюся довольно простой: каким минимальным количеством красок может быть раскрашена карта так, чтобы каждая из соприкасающихся на ней фигур имела свой цвет? Впервые этот вопрос сформулировал англичанин Френсис Гутри в далеком 1852 г. А об ответе - доказательстве или опровержении - математики спорят до сих пор.
Итак, в 1852 г. студент-математик Ф. Гутри обратил внимание своего преподавателя А. де Моргана на «проблему 4 красок». Поначалу солидным математикам она показалась вполне очевидным фактом, не требующим доказательств. Однако уже в 1879 г. в первом томе «Трудов Королевского географического общества» была опубликована статья выдающегося британского математика А. Кэмпе, в которой содержалось предположение о том, что соблюсти все необходимые условия при раскрашивании любой географической карты возможно, используя для этого лишь 4 краски. Это предположение автор статьи достаточно весомо доказывал, применяя внушительные аргументы и вычисления.
Казалось бы: предположили и доказали, так и раскрашивайте. Но математики, как известно, уважают точность. А потому между ними разгорелись споры на эту тему. Одни пытались теорему доказать, другие - опровергнуть. В ходе этих споров уже к концу XIX в. было доказано, что простейшая карта может быть раскрашена с применением трех, а сложнейшая - пяти цветов. Однако случай с применением именно 4 цветов оставался загадкой. Вот карта графств Британии, раскрашенная четырьмя красками [Рис.1]
Доказательство «первопроходца» Альфреда Кэмпе было опровергнуто уже в 1880 г. предложенное в этом же году Питером Тэтом иное доказательство было столь же успешно опровергнуто в 1891 г. После многих неудачных попыток доказать гипотезу для любого числа стран, математики решили доказать её, начиная с малых натуральных чисел. Так П. Франклин в 1913 году доказал гипотезу для карты в которой не более чем 25 стран, со временем он увеличил это число до 38.
С увеличением числа стран лавинообразно растет и число различных вариантов их взаимного расположения, и число вариантов раскраски карт. Проблема становилась совершенно неприступной.
Заслуженный российский математик и инженер, профессор Вячеслав Афанасьевич Горбатов в своей книге, вышедшей в 1964 г. предложил свое классическое доказательство теории четырех красок, занявшее около 30 страниц. Но, по неизвестным причинам, оно прошло незамеченным и не встретило ни подтверждений, ни опровержений.
В апреле 1975 г. редактор Scientific American Мартин Гарднер в статье «6 сенсационных открытий» публикует следующую информацию:
«За последнее время самой большой сенсацией в области чистой математики стало открытие контрпримера к знаменитой проблеме 4 красок. Напоминаю, что эту проблему вызвала гипотеза о том, что любую плоскую карту можно «правильно раскрасить», используя лишь 4 цвета. При этом «правильной» признается такая раскраска, при которой любые 2 области, граничащие между собой, раскрашиваются разными красками. После многолетних исследований эта гипотеза стала примером утверждения, неразрешимого по Гёделю. Однако в ноябре 1974 г. специалист по теории графов У. Макгрегор, профессор университета в Уоппингерс-Фоллз (штат Нью-Йорк), сумел построить карту из 100 областей, раскрасить которую невозможно правильно, используя менее 5 цветов. Статья об этом открытии была опубликована в 1973 г. в номере Journal of Combinatorial Theory, Series В»
Несмотря на откровенную путаницу, материал об этом «открытии» вызвал бурную реакцию читателей. Приведенный в статье рисунок читатели с восторгом раскрашивали «правильно», не жалея на это ни сил, ни времени. Апогеем стало уведомление об иске на 25 млн. долларов от читателя, потратившего более 25 лет на решение проблемы четырех красок, у которого публикация вызвала тяжелейший нервный срыв и инсульт…
В итоге, как сама журнальная статья, так и многомиллионный судебный иск оказались апрельским розыгрышем. Однако математики отнюдь не сочли проблему исчерпавшей себя. Более того, искать решение стало еще интереснее, ведь в распоряжении ученых появились компьютеры! В 1976 г. математики из Иллинойского университета Кеннет Аппель и Вольфганг Хакен с помощью ЭВМ создали 1936 карт, ни одна из которых не могла опровергнуть верность теории. Доказательство заняло сотни листов. На его основании ученые утверждали, что контрпримера этой теореме существовать не может! Идея их доказательства состояла в следующем: сначала доказывается возможность раскраски для карт с числом n стран, 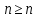 0, затем с помощью компьютера подтверждается возможность раскраски карт и для
0, затем с помощью компьютера подтверждается возможность раскраски карт и для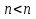 0. Потратив свыше тысячи часов машинного времени, перебрав громадное число вариантов, компьютер подтвердил справедливость гипотезы. Таким образом, вековая проблема четырех красок была решена.
0. Потратив свыше тысячи часов машинного времени, перебрав громадное число вариантов, компьютер подтвердил справедливость гипотезы. Таким образом, вековая проблема четырех красок была решена.
Это доказательство, впервые в математике полученное с помощью компьютера, получило широчайшее признание. Оставались, конечно, отдельные скептики, противившиеся тому, что такое решение не может быть проверено вручную. Возможно, именно поэтому в 1997 г. группа американских ученых предложила новое, более простое доказательство. Впрочем, идеи были аналогичны, а главным помощником исследователей по-прежнему был компьютер. В 2005 г. доказательство снова подтвердилось Джорджсом Гонтиром, который использовал для этого специализированное программное обеспечение.
Пожалуй, на этом историю теоремы о четырех красках можно считать исчерпанной. Впрочем, если вы считаете себя великим математиком, вполне можете попытаться самостоятельно ее доказать либо опровергнуть. А можете просто поиграть, ведь тренировка мозга и развитие логического мышления не вредило до сих пор еще никому.
Я тоже попробовала самостоятельно раскрашивать карты, чтобы убедиться в том, что для раскраски любой конкретной карты хватает четырех красок. Вот, например, раскраска карты России, подтверждающая гипотезу Ф. Гутри, что карту можно раскрасить четырьмя красками [Рис 2].
Раскрашивая карту, я обратила внимание и на то, что её нельзя раскрасить тремя красками. В самом деле, если рассмотреть четыре территории Чукотский автономный округ, Камчатский край, Республика Якутия, Магаданская область, то можно заметить, что Чукотский автономный округ, окружен только тремя этими территориями. Это значит, если территорию Чукотского округа покрасить первым цветом, то для покраски территорий Камчатского края, Республики Якутия, Магаданской области потребуется ещё три цвета.
За время существования теоремы о четырех красках на ее базе были созданы многочисленные логические игры. Поначалу играть в них можно было только на бумаге, затем появились компьютерные варианты. Проверить свои математические способности в этой области можете и вы, используя .
2.2.Игра «4 краски»
Познакомившись с проблемой четырёх красок, известный американский популяризатор математики Стивен Барр придумал логическую игру на бумаге для двух игроков и бесхитростно назвал её «Четыре краски». Вот простые правила этой любопытной игры для двоих: Для этой игры нужны четыре цветных карандаша. Первый игрок начинает игру, рисуя произвольную пустую область. Второй игрок закрашивает её любым из четырёх цветов и в свою очередь рисует свою пустую область. Первый игрок закрашивает область второго игрока и добавляет новую область, и так далее - каждый игрок раскрашивает область соперника и добавляет свою. При этом области, имеющие общую границу, должны быть раскрашены в разные цвета. Проигрывает тот, кто на своём ходу вынужден будет взять пятую краску. Я познакомила с этой игрой своих одноклассников, кто-то ею увлекся. Выигрышной стратегии мы пока не нашли, но некоторые тактические приёмы научились применять. На рисунке ниже приведена типичная картинка, которая остается после очередной игры «Четыре краски» [Рис 3].
Здесь натуральными числами обозначен порядок появления областей на игровой схеме. Понятно, что нечетными числами обозначены области, нарисованные первым игроком, четными - вторым игроком. По правилам игры, когда первый игрок нарисовал 9-ую область, второй должен её закрасить, но для этого ему потребуется пятый цвет, значит, он проиграл.
Это ни в коей мере не означает, что таким рисунком опровергается гипотеза. Раскрасить области этой схемы можно по-другому [Рис 3] так, чтобы выполнялись все условия раскраски, а лишь подтверждает трудность доказательства проблемы. По этому поводу М. Гарднер сказал: «Я не знаю лучшего способа понять трудности, которые встречаются на пути решения проблемы четырёх красок, чем просто поиграть в эту любопытную игру»
Существуют также следующие вариации игры:
-
Карта заранее разбивается случайным образом на области различной величины, и каждый ход игры меняется игрок который закрашивает область, а также меняется цвет (в строгой последовательности). Таким образом каждый игрок закрашивает карту только двумя цветами, а в случае если не может закрасить так, чтобы области, имеющие общую границу были раскрашены в разные цвета. пропускает ход. Игра прекращается, когда ни один из игроков больше не сможет сделать ни одного хода. Выигрывает тот, у кого общая площадь закрашенных им областей больше.
-
Квадрат разбит на несколько квадратов (в основном 4x4), и его стороны окрашены в один из четырех цветов (каждый в разный цвет). Первым ходом закрашивается квадрат прилегающий к стороне, каждый последующий ход можно закрашивать тот квадрат, который прилегает к одному из закрашенных квадратов. Нельзя закрашивать квадрат теми цветами, которыми закрашен один из прилегающих к нему квадратов (в том числе и по диагонали) или прилегающая к квадрату сторона. Выигрывает игрок, делающий последний ход.
Далее приведу несколько задач данной тематики, которые обязаны своим рождением, так долго не решаемой проблемы четырех красок.
2.3.Тематические задачи
Задача 1. Раскрасьте эту карту из 100 стран в четыре цвета так, чтобы соседние страны были окрашены в разные цвета. Решение приведено на рисунке 4.
Задача 2. Рассмотрим все возможные карты на плоскости, образованные прямыми. Примером такой карты может служить обычная шахматная доска. Достаточно ли двух красок для раскрашивания всех таких карт?
Оказывается, достаточно, и доказать это нетрудно. На любой правильно раскрашенной карте интересующего нас типа проведем еще одну, разделив плоскость на две «карты» [Рис.5 Для раскраски любой карты, образованной прямыми, пересекающими всю ее поверхность от одного края листа до другого, достаточно двух красок].
Каждая из новых карт в отдельности раскрашена правильно, но к новой «границе» только что проведенной прямой примыкают пары областей, окрашенных в один и тот же цвет. Для того чтобы восстановить правильную раскраску всей карты в целом, нужно перекрасить одну из карт-половинок (какую именно - безразлично), изменив окраску каждой из областей на противоположную. Карта над черной прямой «обращена» - перекрашена так, словно «отрицательные» области стали «положительными» и наоборот, и, как нетрудно видеть, вся карта раскрашена правильно.
Для завершения доказательства рассмотрим плоскость, разделенную на две области одной-единственной прямой. Такую карту, разумеется, можно раскрасить в два цвета. Проведем вторую прямую и раскрасим новую карту, переменив все цвета по одну сторону от новой прямой на противоположные. Затем проведем третью прямую и т. д. Ясно, что предложенный метод пригоден при любом числе прямых. Следовательно, «методом полной математической индукции» мы доказали теорему о возможности раскраски в два цвета всех карт, образованных прямыми на плоскости. Доказательство можно несколько обобщить на случай более разнообразных карт, например таких, как карта на рис. 2, образованная либо кривыми, пересекающими весь лист от одного края до другого, либо замкнутыми кривыми без самопересечений [Рис.6. Двух красок достаточно для раскрашивания карты, образованной либо линиями, идущими от одного края листа до другого, либо замкнутыми кривыми].
Проведя еще одну кривую, пересекающую всю карту от одного ее края до другого, мы должны, как и прежде, изменить все цвета по одну сторону от кривой на противоположные. Если вновь проведенная кривая замкнута, то изменить нужно окраску всех областей, попавших внутрь кривой, или, если угодно, всех областей, оказавшихся снаружи. Замкнутые кривые могут иметь и точки самопересечения, но в этом случае перекрашивание областей более сложно.
Заметим, что на всех приведенных здесь двухцветных картах все вершины четны (напомним, что вершиной называется точка, в которой сходятся границы более двух стран), то есть в каждой вершине сходится четное число границ. Можно показать, что любую карту на плоскости можно раскрасить в два цвета тогда и только тогда, когда все ее вершины четны. Это утверждение известно как «теорема о двухцветных картах». Нетрудно видеть, что на торе эта теорема не выполняется. Для этого достаточно скатать в трубку квадратный лист бумаги, расчерченный на девять маленьких квадратов (наподобие игрового поля для крестиков и ноликов), а концы трубки склеить. Все вершины на таком «клетчатом» торе четны, но для его раскрашивания необходимо взять три краски.
Задача 3. На плоскости нарисовано n окружностей. В каждой окружности проведено по хорде так, что хорды двух окружностей имеют между собой самое большое одну общую точку (рис.7.1). Докажите, что получившуюся карту на рисунке слева всегда можно раскрасить тремя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Доказательство. Идею доказательства проведем для трёх окружностей с хордами, хотя все рассуждения можно обобщить на случай, когда на плоскости нарисовано n окружностей с хордами. Состоит она в следующем:
первая, малая окружность и её хорда разбивает плоскость на три части. Во всех областях первой части поставим по 0, во всех областях второй части поставим 1, во всех областях третьей части поставим 2 (рис.7.2);
вторая, средняя окружность и её хорда разбивает плоскость на три части. Во всех областях первой части поставим по 0, во всех областях второй части поставим 1, во всех областях третьей части поставим 2 (рис. 7.3);
третья, большая окружность и её хорда разбивает плоскость на три части. Во всех областях первой части поставим по 0, во всех областях второй части поставим 1, во всех областях третьей части поставим 2 (рис. 7.4).
При этом каждой области будет соответствовать три числа, найдем их сумму (рис. 7.5), и числа каждой области заменим остатком от деления его на 3 (рис.7. 6).
Области, у которых этот остаток равен 0, закрасим синей краской;
области, у которых этот остаток равен 1, закрасим желтой краской;
области, у которых этот остаток равен 2, закрасим красной краской.
Полученная таким образом раскраска (рис. 7.7) удовлетворяет условия задачи.
-
Заключение
Задача о четырех красках относится к самой элементарной ветви топологии, называемой «геометрией расположения». Это начало топологии, ее наглядная часть. Задача же о четырех красках замечательна тем, что ее можно объяснить и первокласснику, и очень хочется нарисовать такую карту, для раскраски которой потребовалось бы пять цветов. Кстати, первоклассникам именно так и надо ставить задачу: не говорить им, что всегда достаточно четырех красок, а просить нарисовать карту, для которой четырех красок не хватает, и только спустя несколько дней сообщить, что это невозможно. Благодаря таким задачам любой человек с улицы сразу понимает, что математика очень элегантна. Ясное понимание несуществования чего-то - чисел ли с заданными свойствами, или способов построения геометрических фигур, или алгоритмов - создает особый дискурс, который можно было бы назвать культурой невозможного. И культура невозможного, и предпринимаемые математикой попытки познания бесконечного значительно расширяют горизонты мышления. Все это, ломая традиционный стереотип математики как сухой цифирии, создает ее образ как живой области знания.
В заключение хочу отметить следующее: хотя теорема доказана и принята математическим сообществом, но у части математиков её доказательство вызывает определенное недоверие в той его части, где значительную часть рутинных проверок выполнял компьютер.
Сами авторы доказательства сообщают: "Читатель должен разобраться в 50 страницах текста и диаграмм, 85 страницах с почти 2500 дополнительными диаграммами, 400 страницами микрофишей, содержащими еще диаграммы, а также тысячи отдельных проверок утверждений, сделанных в 24 леммах основного текста. Вдобавок читатель узнает, что проверка некоторых фактов потребовала 2000 часов компьютерного времени, а при проверке вручную потребовалось бы гораздо больше. Статьи устрашающи по стилю и длине, и немногие математики прочли их сколько-нибудь подробно".
Несмотря на все разногласия среди математиков решение проблемы четырёх красок есть первая математическая теорема, при доказательстве которой впервые был использован компьютер, и является примером неклассического доказательства в современной математике.
«Так решена ли проблема четырех красок?», - каждый вправе задать себе такой вопрос. Я думаю, правильный ответ на него даст время, нужно подождать.
Литература
-
Л. Беве, Любая карта на плоскости может быть раскрашена в четыре цвета, Квант, 1977 г., №1;
-
Е. Дынкин, В.Успенский, Математические беседы, М и Л, ГИТТЛ, 1952 г.;
-
А. А. Зыков. Основы теории графов. - М.: Вузовская книга, 2000. - С. 367-386.
-
Журнал //Наука и жизнь. - 1979. - № 3. - С.80
-
Методы четырехцветной раскраски вершин плоских графов. - М.: КомКнига, 2000. - 48 с. - 2005 экз. -
-
Р.Курант, Г.Роббинс
-
Самохин А. В. //. - 2000. - № 7. - С. 91-96.
-
Родионов В. В. Методы четырехцветной раскраски вершин плоских графов. - М.: КомКнига, 2000. - 48 с. - 2005 экз. -
-
Рингель Г. Теорема о раскраске карт / Перевод с английского В. Б. Алексеева. - М.: Мир, 1977. - 256 с. - книга с доказательством проблемы для всех поверхностей, кроме плоскости и сферы
-
И. Шарыгин, Л. Ерганжиева, Наглядная геометрия, 5-6 кл., М, Дрофа, 2007 г.
Приложение
Рис 1. Карта графств Британии. 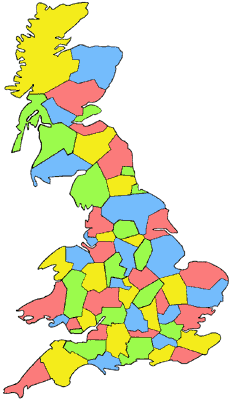
Рис2. Карта России. 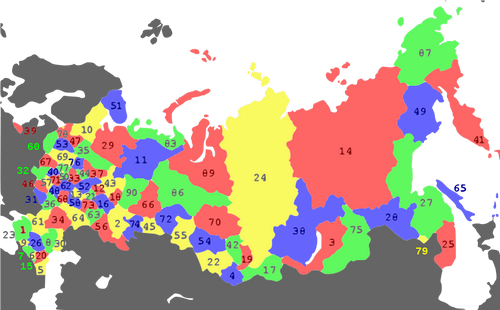

Рис 3. Игра 4 краски.
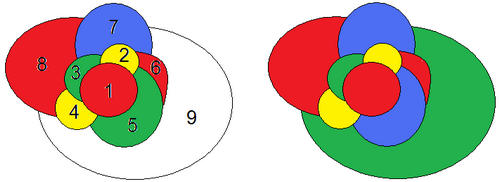
Рис 4. Задача 1.
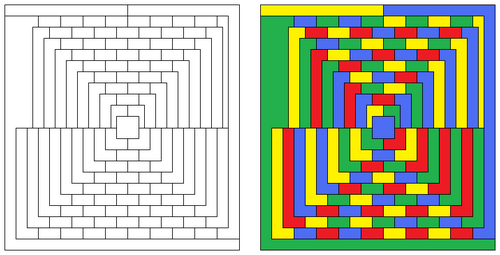
Рис. 5. Для раскраски любой карты, образованной прямыми, пересекающими всю ее поверхность от одного края листа до другого, достаточно двух красок
Рис.6. Двух красок достаточно для раскрашивания карты, образованной либо линиями, идущими от одного края листа до другого, либо замкнутыми кривыми.

Рис 7. Задача 3.

20