Межрегиональная научно-практическая

конференция студентов и старшеклассников

«Образование как фактор конкурентоспособности выпускника в условиях рыночной экономики »

Наименование секции

общепрофессиональные и естественно-научные дисциплины

Наименование работы

Математический цветник

Фамилия и имя автора работы

Сарычева Вера

Учебное заведение

МБОУ Избердеевская сош

Петровского района

Тамбовской области

Научный руководитель:

Сарычева Татьяна Юрьевна,

учитель математики

г. Мичуринск

2016

Содержание

Введение._________________________________________________3

Глава 1. Кривые Гранди

1. Исторические сведения о Гранди Луиджи Гвидо._____________________________________________5

2. Понятие полярной системе координат.________________7

3. Изучение различных форм кривых Гранди,

заданных в полярной системе координат.___________8

Заключение._______________________________________________11

Список литературы.________________________________________13

Приложение.______________________________________________14

Введение.

В природе мы встречаем большое разнообразие видов цветов и их форм. Однажды итальянский геометр Гвидо Гранди (1671-1742), работая с полярной системой координат, решил воссоздать с помощью кривых прекрасные розы. Теория этих кривых была изложена им в сочинении «Flores geometrici ex rhodanearum et claelarum descriptione resultantes». «Розы» Гвидо Гранди радуют глаз правильными и плавными линиями, их очертания предопределены специально подобранными математическими зависимостями. Позже немецкий геометр XIX века Хабеннихт, очарованный результатами Гранди, также решил заняться математическим «растениеводством». Меня заинтересовала следующая проблема: от чего зависит изменение формы цветков «роз» и количество лепестков в цветках.

Гипотеза, которая легла в основу данной работы состоит в том, что в живой природе совершенство очертаний и форм цветов можно задать математическими зависимостями, то есть существует основа красоты.

Объект - кривые «розы Гранди».

Предмет - исследование зависимости очертаний и форм лепестков от изменения коэффициентов в формуле, задающей кривую Гранди.

Цель: выяснить, как изменяется форма «роз» при изменении коэффициентов в формуле, задать графически данную зависимость, показать практическое использование данных кривых в искусстве и дизайне.

Задачи, которые были поставлены в этой работе:

- исследовать доступную научную и научно - популярную

литературу по данной теме;

- проанализировать собранный материал;

- построить в полярной системе координат несколько кривых Гранди, выяснить зависимость формы кривой от коэффициентов в формуле;

- сделать обоснованный вывод по теме работы;

- применить полученные сведения на практике.

Задачи и цель работы определили следующие методы работы: хронологический, который помог восстановить историю появления кривых, названных «розами Гранди»; сопоставительный, с помощью которого был проанализирован собранный материал, и метод анализа и синтеза.

Данная работа позволяет по-новому, с точки зрения математики, посмотреть на красоту окружающего мира, понять, что математика - прикладная наука, позволяющая описывать эту красоту.

Глава 1.

Кривые Гранди.

1. Исторические сведения о Гранди Луиджи Гвидо.

Гранди Луиджи Гвидо (1671 - 1742) был итальянским монахом, священником, философом, математиком и инженером.

Он родился 1 октября 1671 в Кремоне, Италия и окрещен Луиджи. Гранди получил образование в иезуитском колледже. В 1687 году он поступил послушником в приют монахов в Ферраре и принял имя Гвидо. В 1693 году он был отправлен в монастырь Святого Григория Великого, чтобы завершить свои исследования в философии и теологии в рамках подготовки к священству. Был назначен преподавателем философии и теологии в монастыре во Флоренции в 1694 году. Похоже, что именно в этот период его жизни он проявил интерес к математике. Он делал свои исследования в частном порядке и был назначен профессором философии в монастыре Св. Григория в 1700 году.

К 1707 году Гранди заработал такую ​​репутацию в области математики, что был назначен математиком великого герцога Тосканского, Козимо III Медичи. Его трактат о квадратуре (1703) открыл Италии исчисления Лейбница. Он был также автором нескольких популярных учебников.

Он также делал успехи в теоретической и практической механике. Его исследования в области гидравлики вызвали значительный интерес со стороны правительств стран Центральной Италии.

В 1701 Гранди опубликовал результаты исследования конических локсодромий. Он выступил в качестве соавтора в издании первого флорентийского издания трудов Галилея. В 1703 году в его «Записке о трактате Галилея о естественном движении" он дал первое определение кривой versiera , (от лат.vertere -включить). Эта кривая была позже изучена одной из немногих женщин-ученых Марией Аньези.

В 1709 году он посетил Англию, где был избран членом Королевского общества. Пизанский университет присвоил ему звание профессора математики в 1714 году. Именно там он умер 4 июля 1742 года.

В математике Гранди известен его работой Flores geometrici (1728), изучавшей розы - кривые, которые имеют форму лепестков цветка. Он назвал розы кривой rhodonea и назвал кривую Clelia в честь графини Клелии Борромео.

1.2 Понятие полярной системе координат.

Изучая кривые, Гранди работал в полярной системе координат.

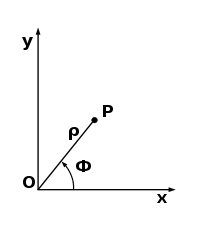
Полярная система координат - двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами - полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов. Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.

1.3 Изучение различных форм кривых Гранди, заданных в полярной системе координат.

Уравнение «розы» Гвидо Гранди в полярных координатах имеет вид:

ρ= m*.

Задавая параметр k= отношением натуральных чисел, можно получить замкнутые кривые, при определенных условиях превращающиеся в лепестковые розы или ажурные розетки, которые могут служить элементами декора или орнамента.

Рассмотрим уравнение «розы» при m=1,k=1:

ρ= .

Построим в полярной системе координат кривую, заданную этим уравнением. Примем 0ᵒ≤ φ≤ 360ᵒ с шагом 10ᵒ.Вычисляя синусы заданных углов, отметим точки в плоскости ( см. приложение1).

Процесс построения кривой по заданным полярным координатам трудоемкий. Удобнее воспользоваться программой для построения кривых в полярной системе координат Advanced Grapher 2.2. Совместим полярную систему координат с прямоугольной декартовой системой координат так, чтобы полюс совпал с началом координат, а полярная ось - с осью абсцисс.

При построении кривой, заданной уравнением

ρ=2* (m=2, k=1),

оказалось, что форма кривой не изменяется, а изменяется лишь размер

«лепестка» : он увеличился в 2 раза ( см. приложение 2).

Очевидно, что при построении кривой, заданной уравнением

ρ=3* (m=3, k=1),

«лепесток» увеличится в 3 раза по сравнению с первым. Значит, с изменением коэффициента m изменяется размер кривой.

Построим теперь кривую, заданную уравнением

ρ= .

Получилась четырехлепестковая «роза», симметричная относительно оси абсцисс, оси ординат и начала координат (см. приложение 3).

При построении кривой, заданной уравнением

ρ=2 ,

оказалось, что размер «розы» увеличился в 2 раза, как и предполагалось ( см. приложение 4).

Рассмотрим кривую, заданную уравнением

ρ= .

Получилась трехлепестковая «роза» ( см. приложение 5).

При построении кривой, заданной уравнением

ρ=2* ,

также получилась трехлепестковая «роза», размер которой оказался в 2 раза больше по сравнению с предыдущей ( см. приложение 6).

Рассмотрим кривую, заданную уравнением

ρ= .

Данная кривая представляет собой цветок, состоящий из 8 лепестков. Эту кривую еще называют полярной розой.

При построении кривой, заданной уравнением

ρ= ,

также получилась полярная роза, размер которой в 2 раза больше предыдущей.

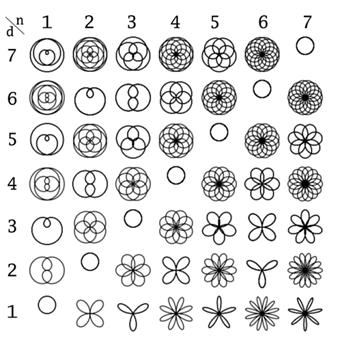
Итак, коэффициент задает количество лепестков: при нечетном получаем - лепестковую розу, при нечетном получаем - лепестковую розу.

Теперь рассмотрим уравнение кривой

ρ= m*, если - дробное число.

Примем, например, =, то есть

ρ= при (0).

При построении кривой «цветок» получается неполным ( см. приложение 9). Однако, если задать 0, то получаем полный «цветок» ( см. приложение 10).

Кривая, заданная уравнением

ρ=2*

при 0выглядет неполной ( см. приложение 11). Зададим угол 0. В этом случае получим полный вид кривой (приложение 12).

Аналогично, выполняя построение кривой, заданной уравнением

ρ=2* ,

будем получать неполный вид кривой при , , . При получается полный вид кривой ( см. приложение 16).

Итак, изменяя в коэффициенте числа n и d, можно получить разнообразные кривые ( см. приложение 17).

Заключение.

Исследовав, как изменяются кривые Гвидо Гранди, заданные в полярной системе координат r=m* в зависимости различных значений параметров k, m, мы установили связь между количеством лепестков, их формул и симметричности получившегося рисунка. Когда мы получали «розы» из четного количества лепестков, рисунок был симметричен относительно начала координат и осей координат. Если мы получали цветы из нечётного количества лепестков, то рисунок был симметричен только относительно оси ординат.

В ходе исследовательской работы мы получили большое разнообразие форм «роз» Гвидо Гранди, которые дают фантазию для их применения. С помощью выращенных цветов, различных кривых в полярных координатах и графических редакторов мы можем сделать, например, различные рисунки, рамки-орнаменты или украсить ими фон открыток. Мне захотелось расписать тарелку, применив в виде орнамента кривую Гранди. Сначала я изобразила эскиз узора на бумаге( см. приложение 18). Для узора в центре я использовала кривую, заданную уравнением

ρ=2* .

Для орнамента, расположенного по краям тарелки я применила кривую, заданную уравнением

ρ=2 .

Затем я нанесла выбранный узор на стеклянную тарелку и раскрасила витражными красками. У меня получился красивый орнамент. (см. приложение 19).

Возле нашей школы каждую весну учащиеся вместе с учителями разбивают клумбы. Я предложила учителю биологии разбить клумбу в виде розы Гранди. Конечно, предстоит работа по построению эскиза клумбы, выбору цветов для клумбы. Надеюсь, что моя идея воплотится в жизнь будущей весной.

Гипотеза, которая была поставлена в работе, подтвердилась. Математика- действительно очень красивая наука. Она находит свое применение не только в технических науках, но и в дизайне и искусстве.

Интернет-ресурсы.

1. matematikaiskusstvo.ru/rosesgrandy.html - математика и искусство.

2. mathworld.wolfram.com/Rose.html- формы кривых Гранди.

3. sibac.info/11124 - математическое моделирование в дизайне и архитектуре малых форм.

4. gvidograndi.jimdo.com/</ - розы Гвидо Гранди.

Приложения

Приложение 1.

Построение кривой, заданной уравнением ρ= .

-0,98

1

ᵒ

280

290

300

310

320

330

340

350

360

ρ

-0,98

-0,94

-0,87

-0,77

-0,64

-0,5

-0,34

-0,17

0

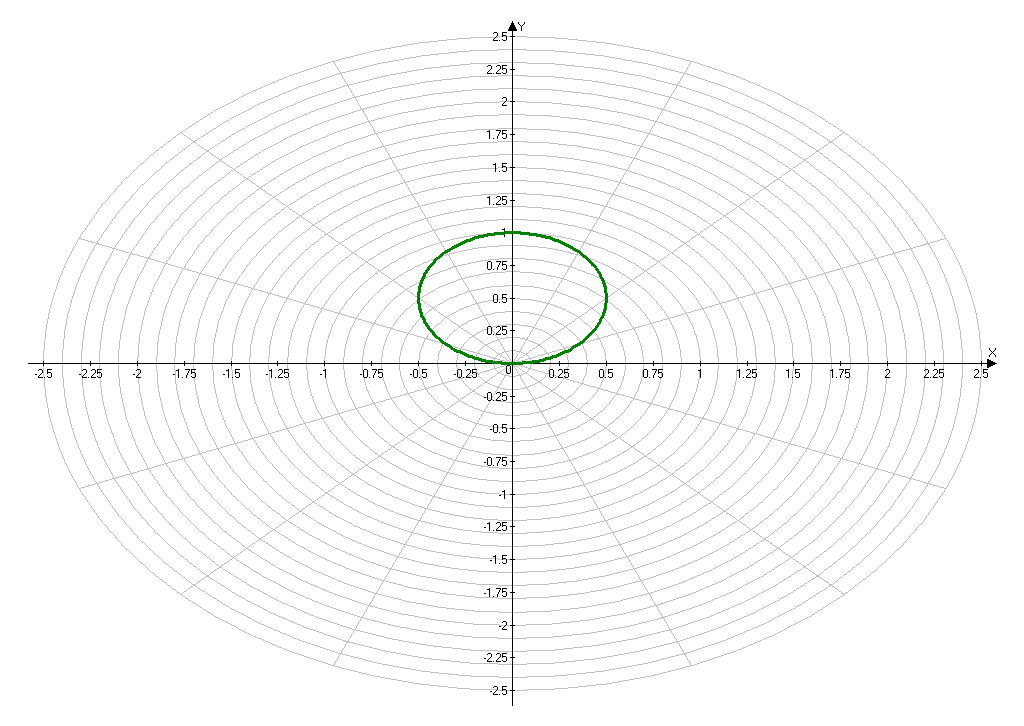
Приложение 2.

Построение кривой, заданной уравнением ρ=2* .

-1,96

-2

ᵒ

280

290

300

310

320

330

340

350

360

ρ

-1,96

-1,86

-1,72

-1,52

-1,28

-1

-0,68

-0,34

0

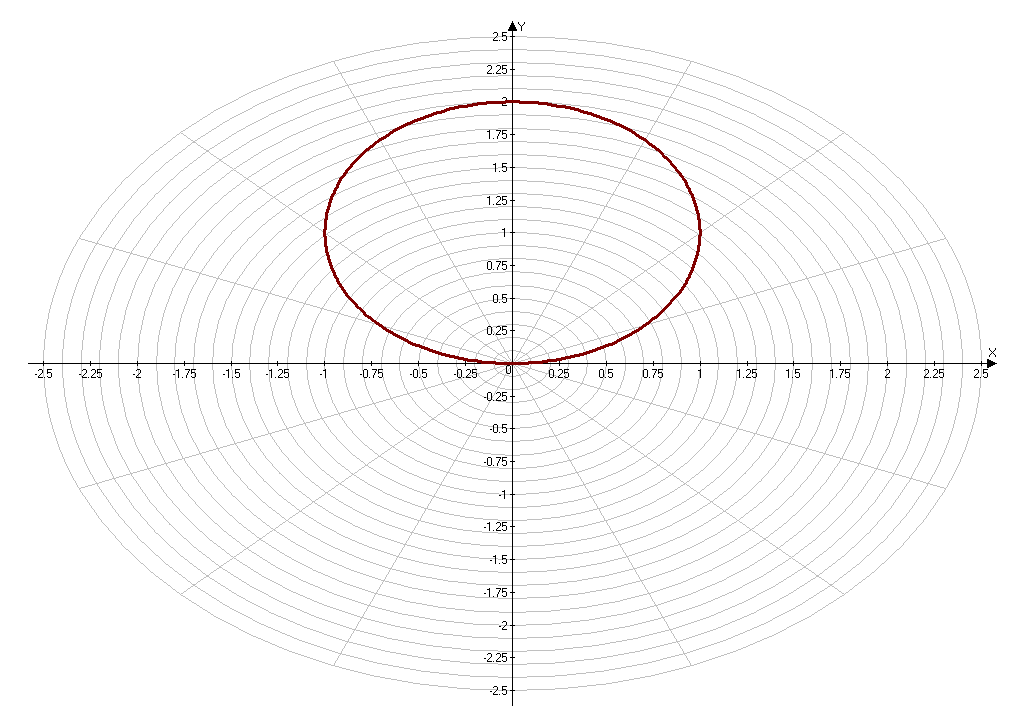
Приложение 3.

Построение кривой, заданной уравнением ρ=

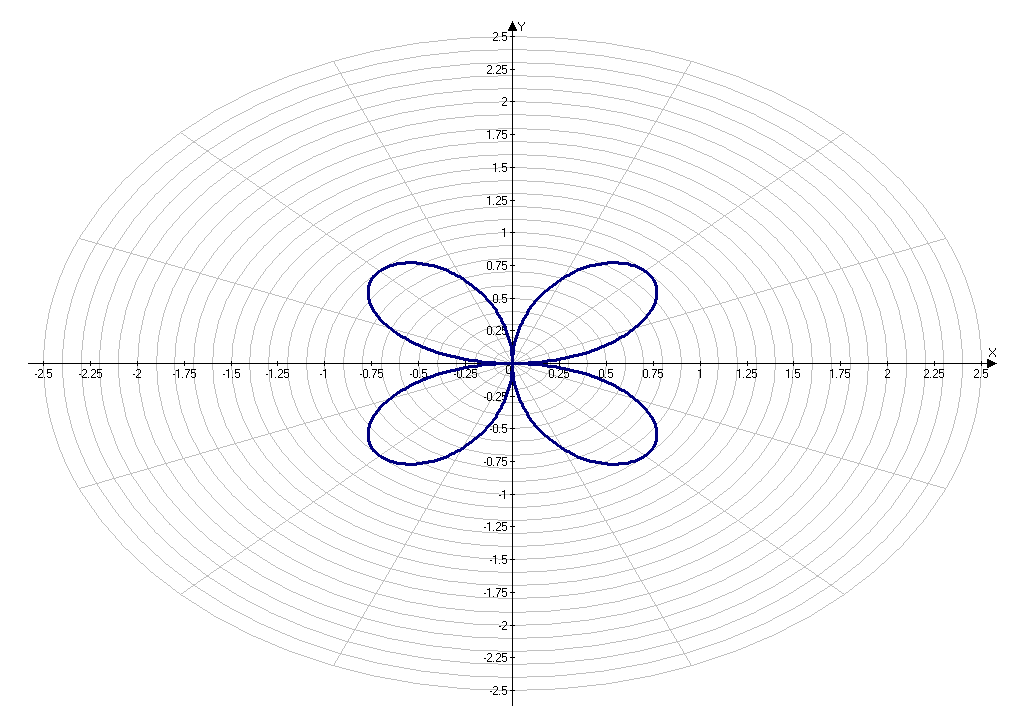
Приложение 4.

Построение кривой, заданной уравнением ρ=2 .

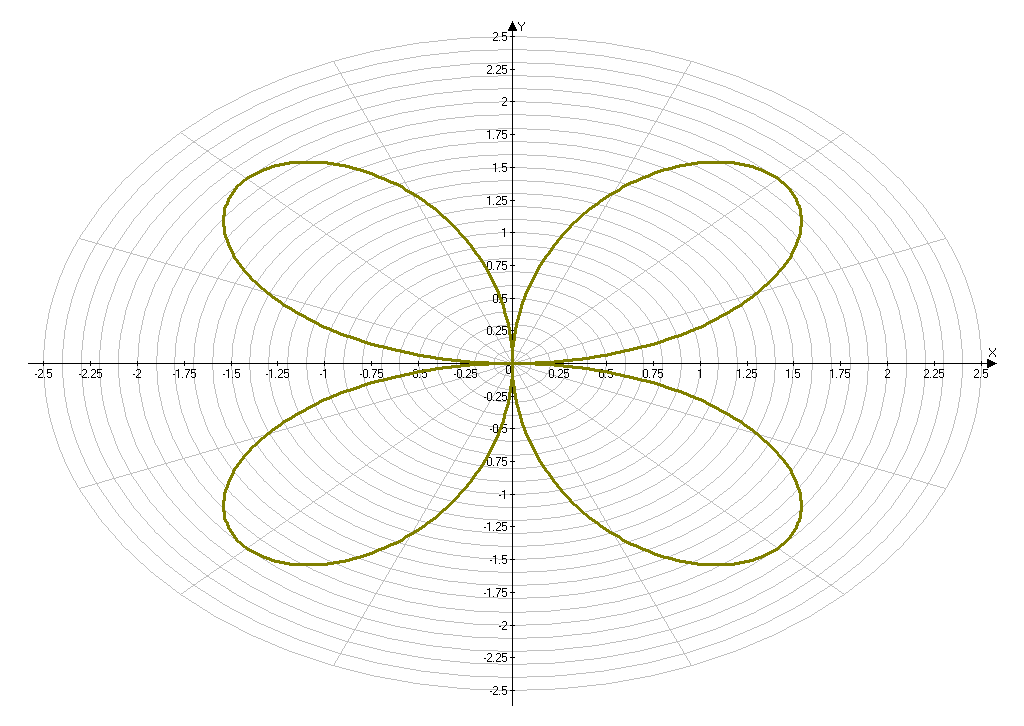
Приложение 5.

Построение кривой, заданной уравнением ρ= .

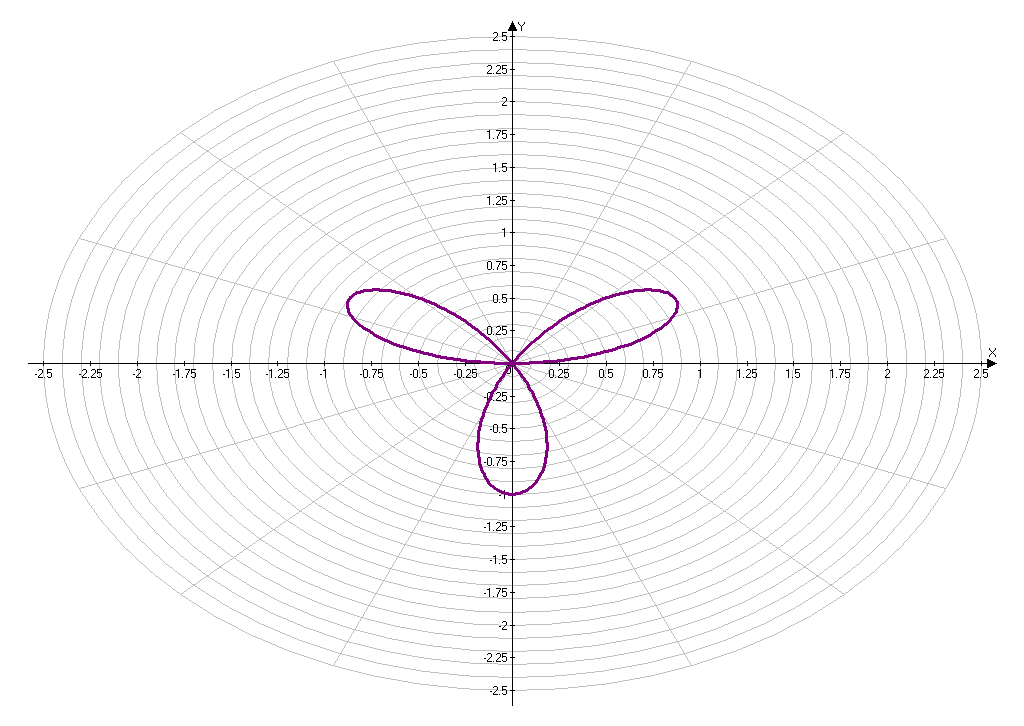
Приложение 6.

Построение кривой, заданной уравнением ρ= .

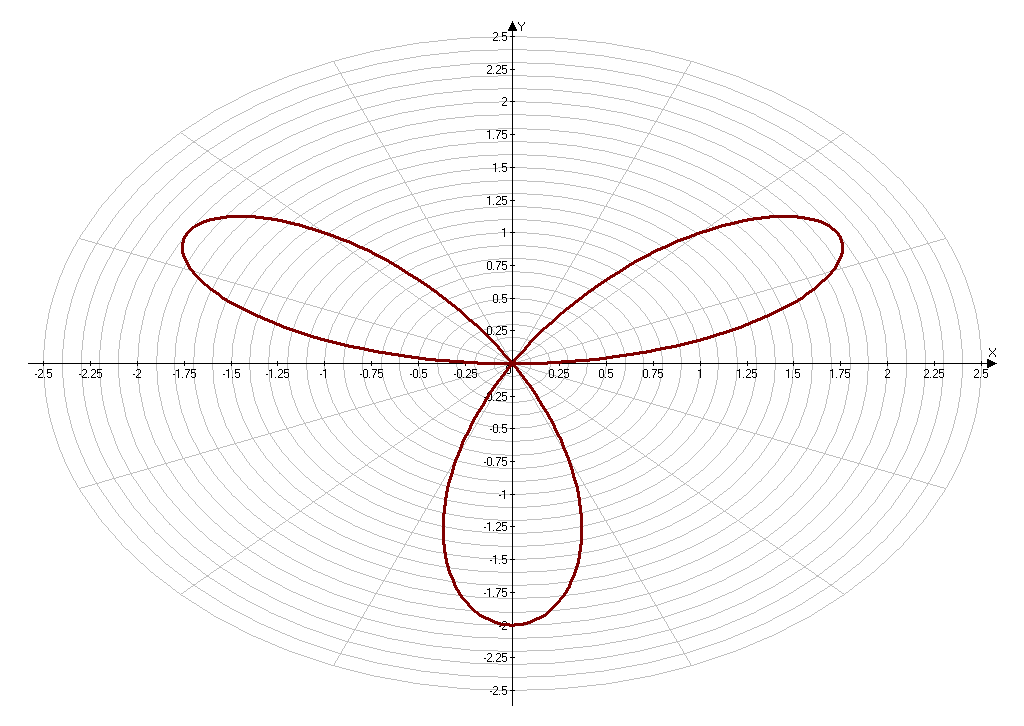
Приложение 7.

Построение кривой, заданной уравнением ρ= .

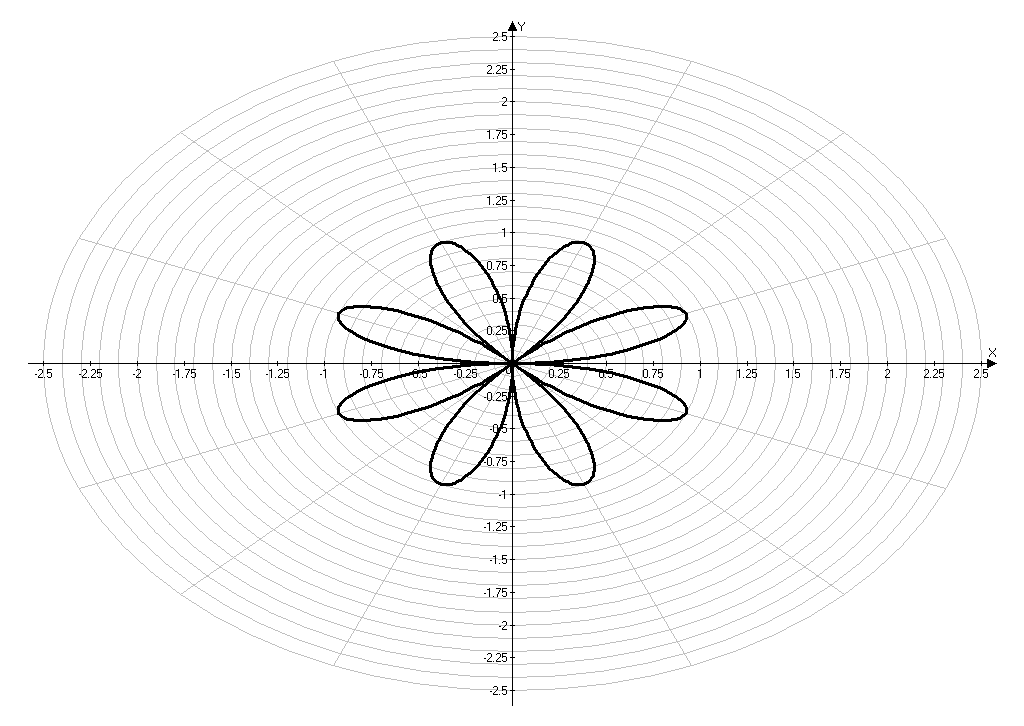
Приложение 8.

Построение кривой, заданной уравнением ρ= .

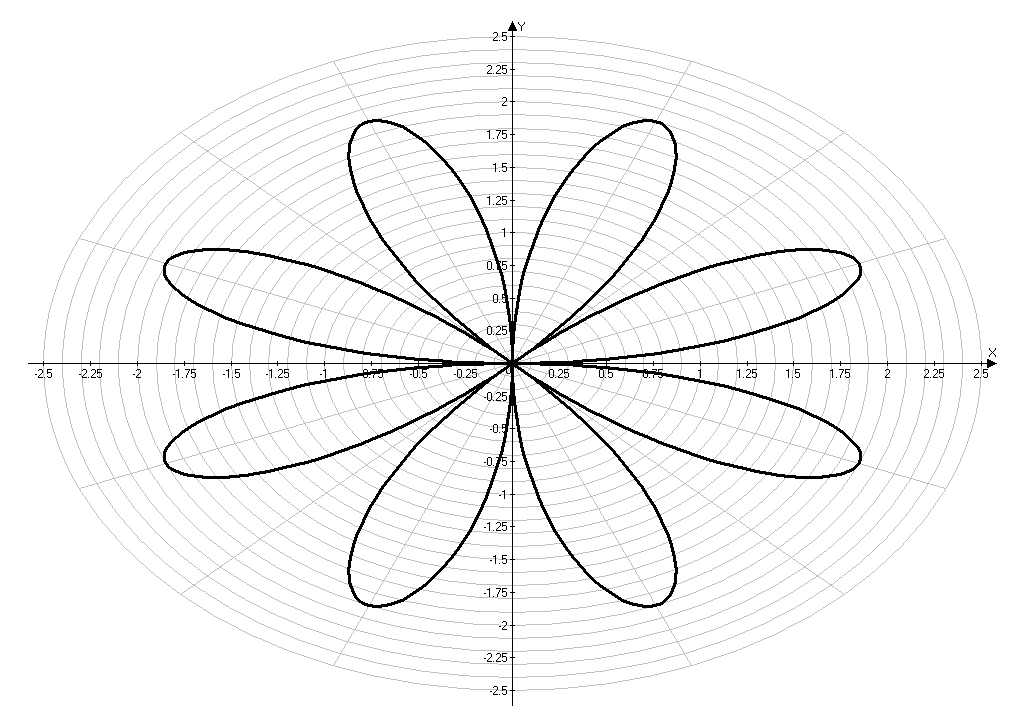
Приложение 9.

Построение кривой, заданной уравнением ρ= (0).

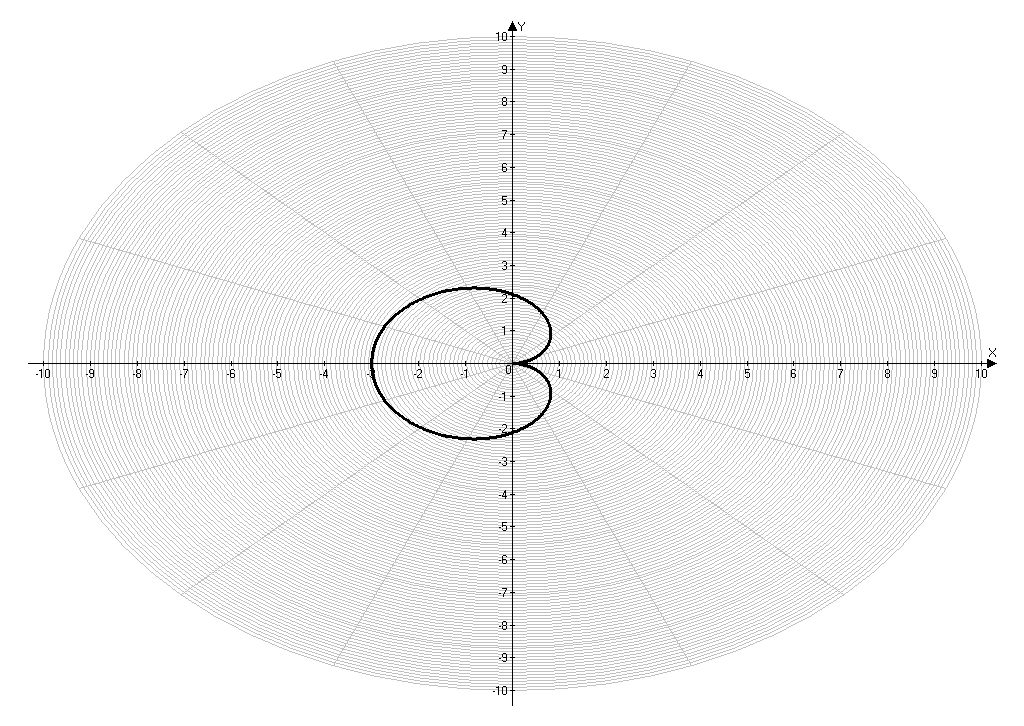
Приложение 10.

Построение кривой, заданной уравнением ρ= (0).

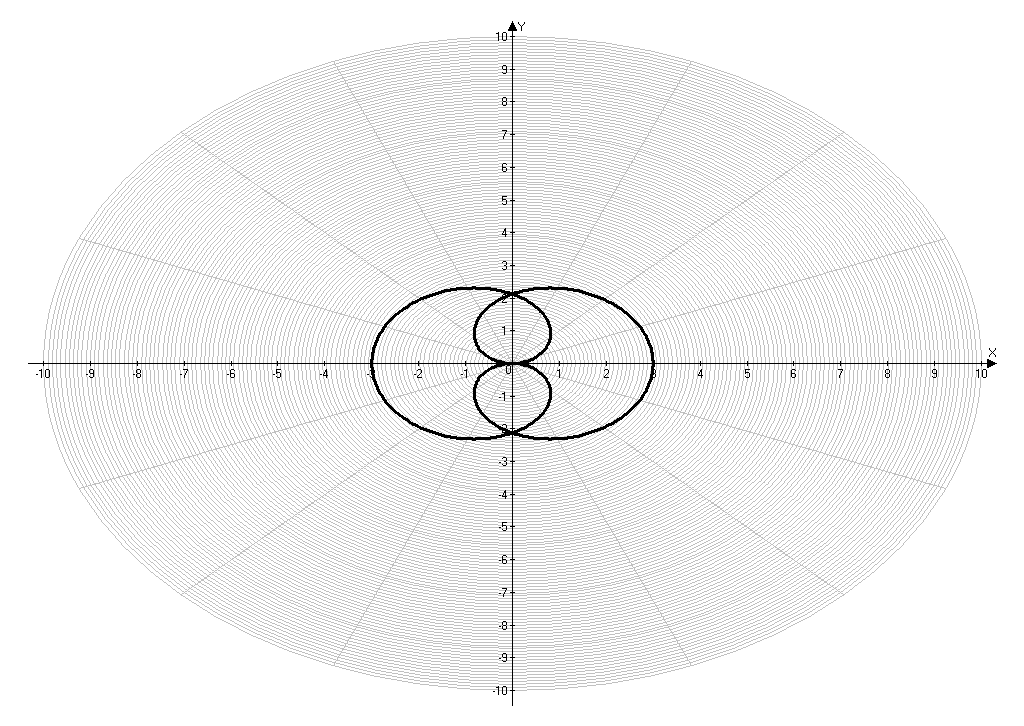
Приложение 11.

Построение кривой, заданной уравнением ρ=2* (0).

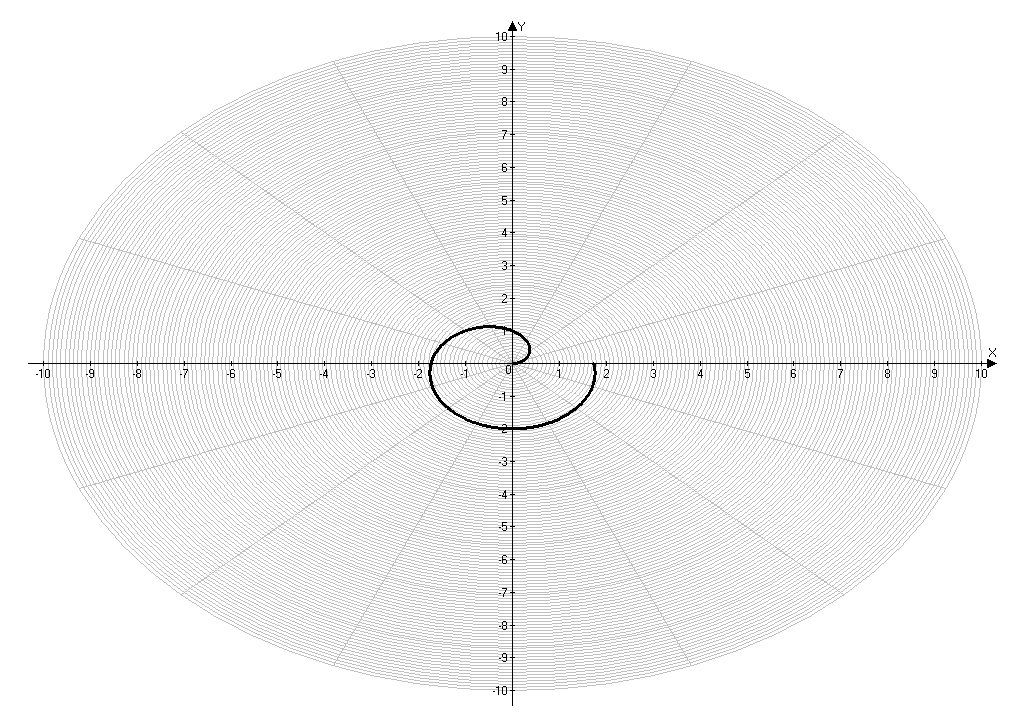
Приложение 12.

Построение кривой, заданной уравнением ρ= (0).

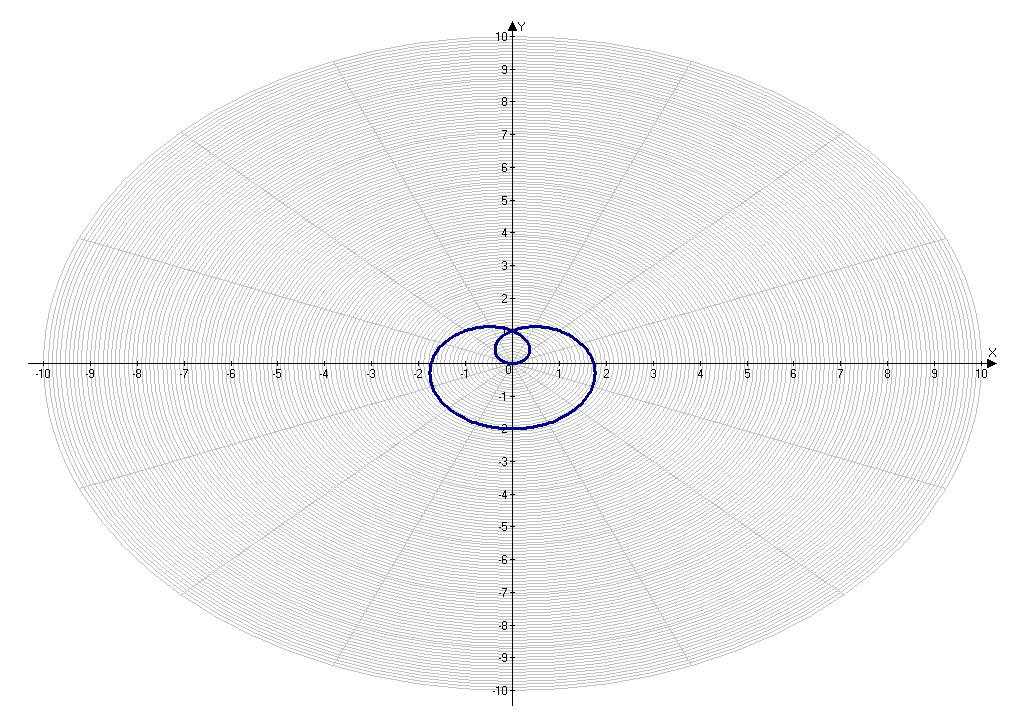
Приложение 13.

Построение кривой, заданной уравнением ρ= (0).

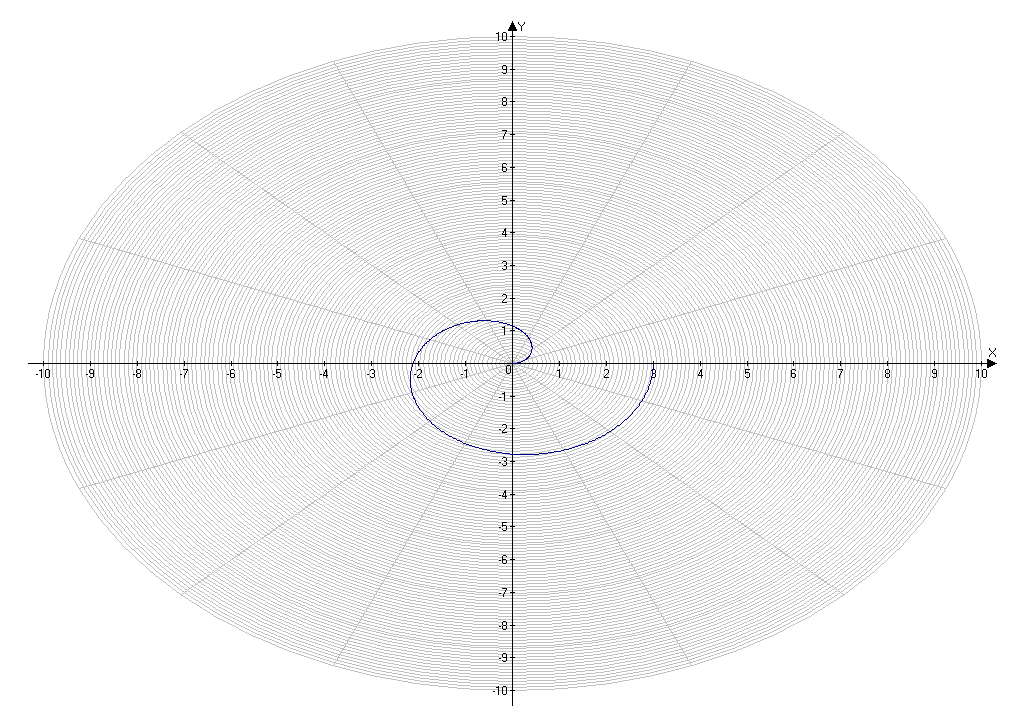
Приложение 14.

Построение кривой, заданной уравнением ρ= (0).

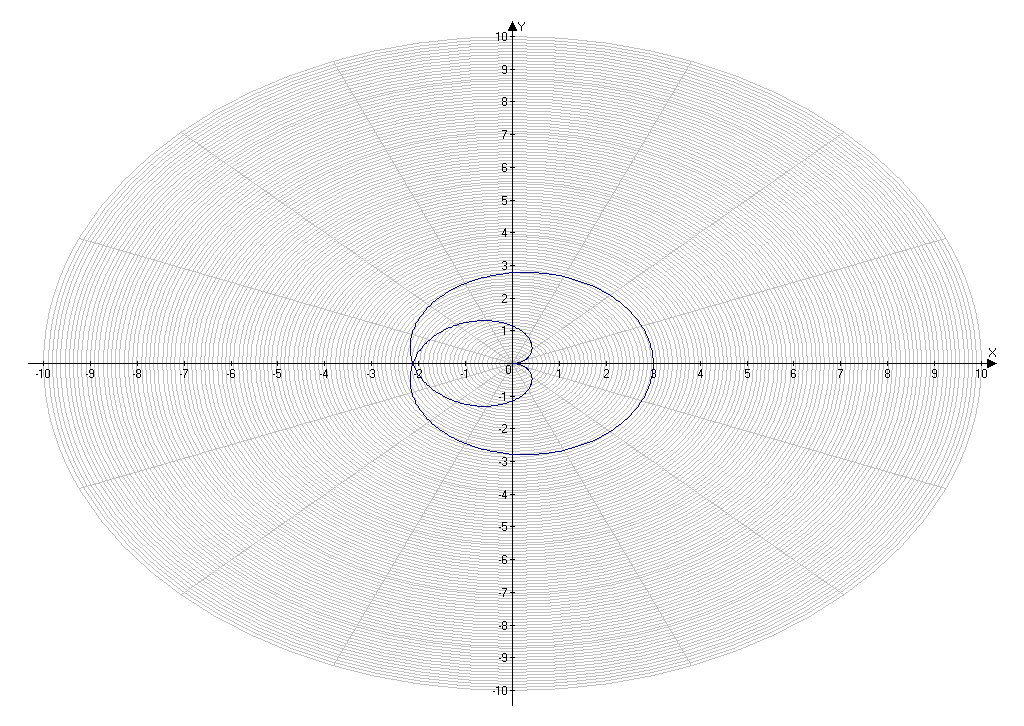
Приложение 15.

Построение кривой, заданной уравнением ρ= (0).

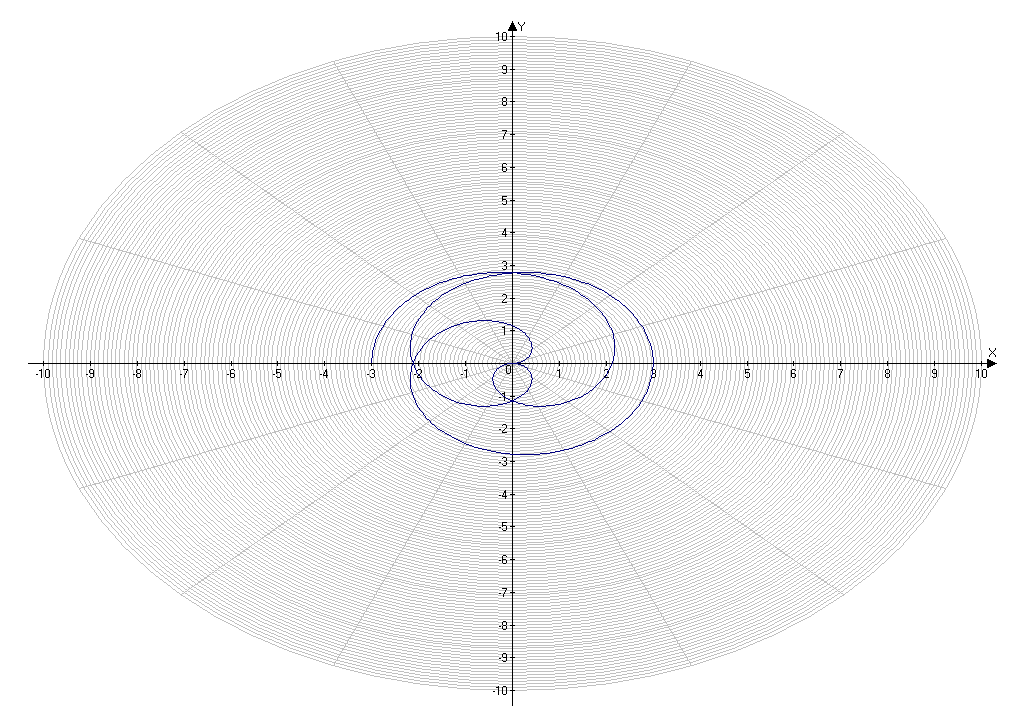
Приложение 16.

Построение кривой, заданной уравнением ρ= (0).

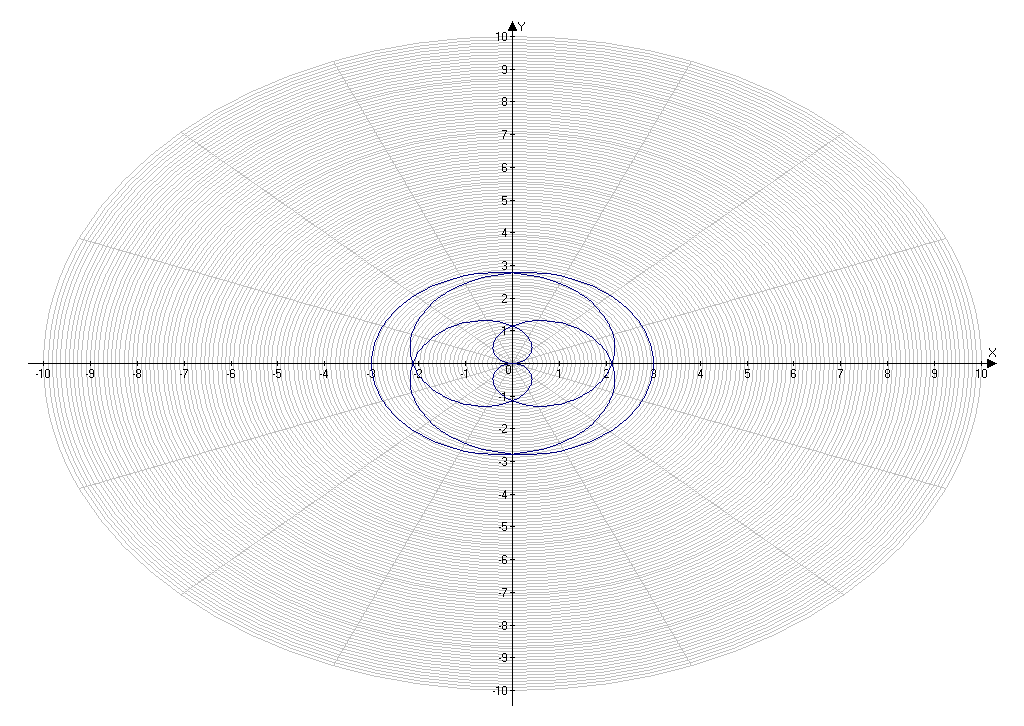
Приложение 17.

Вид кривой, заданной уравнением ρ= m*, если .

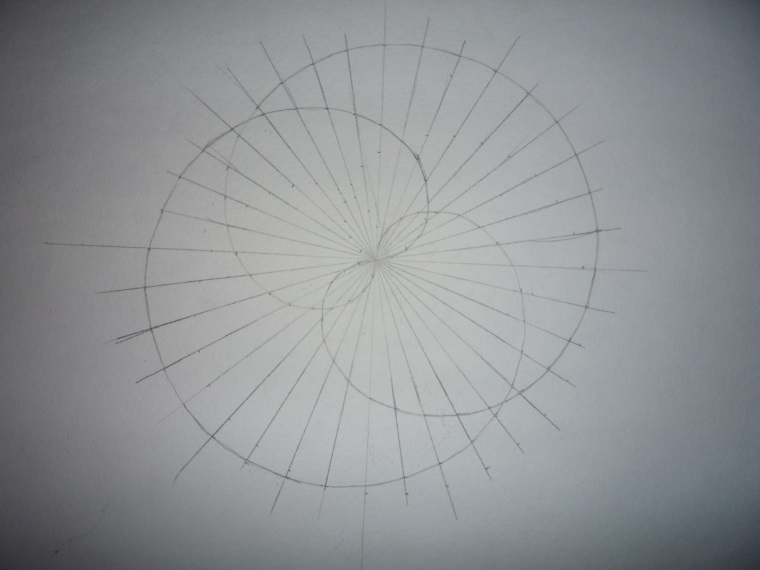
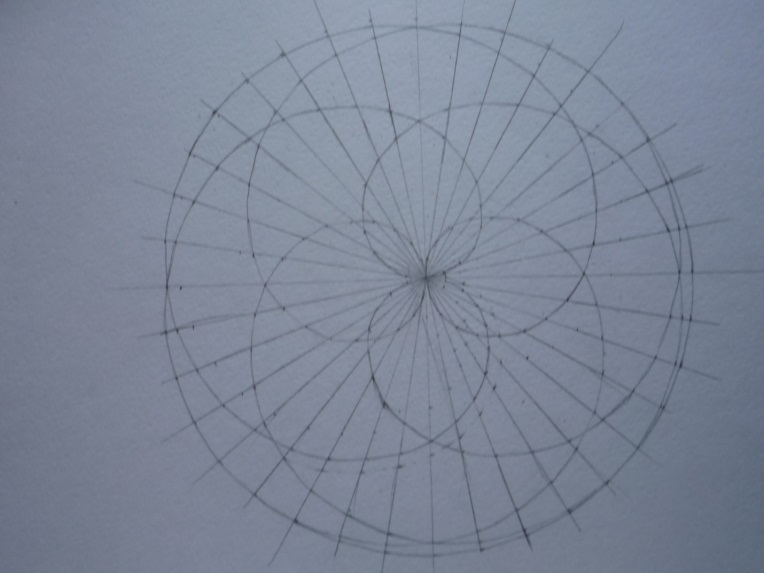
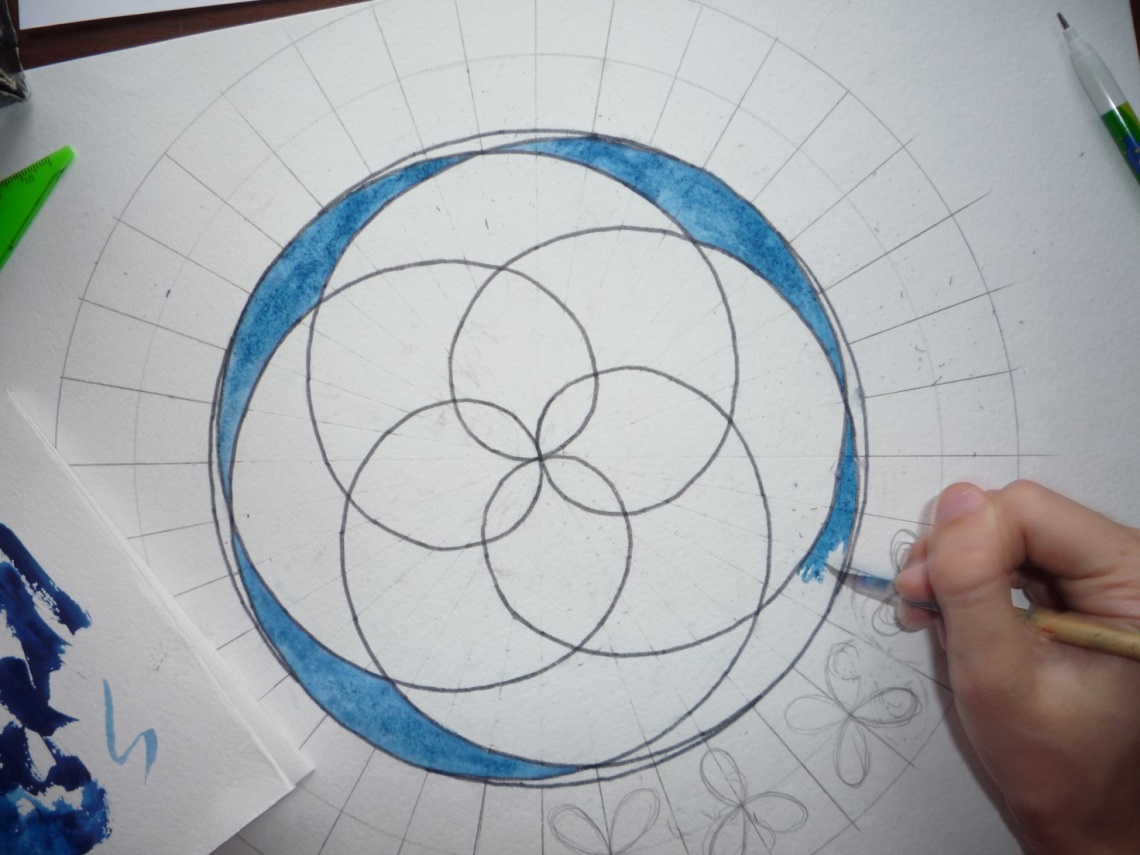
Приложение 18.

Этапы построения эскиза орнамента для росписи тарелки.

Приложение 19.

Использование кривой Гранди в качестве орнамента на стеклянной тарелке.