- Учителю
- Рабочая программа 10 класс
Рабочая программа 10 класс
|
ПРИНЯТО На заседании методического Совета МКОУ БСОШ №97 Протокол №__ от «___» __________2015_г. |
Утверждаю Директор МКОУ БСОШ № 97 Терехина Н.А. ___________________ «_____»____________2015_г. |
Муниципальное Казенное Общеобразовательное Учреждение
Брединская Средняя Общеобразовательная Школа№97
РАБОЧАЯ ПРОГРАММА
Математика
(название предмета, дисциплины, курса, модуля)
Математика
(образовательная область)
10 класс III общеобразовательная ступень
(класс, ступень)
Асташенко Светлана Анатольевна
(ФИО учителя)
Бреды. 2015г.
Рабочая программа составлена в соответствии с нормативными документами:
Нормативные документы
(общие, для реализации Федерального государственного образовательного стандарта общего образования и Федерального компонента государственного образовательного стандарта)
Федеральный уровень
1. Федеральный закон от 29.12.2012 г. № 273-ФЗ «Об образовании в Российской Федерации» (редакция от 31.12.2014 г. с изменениями от 06.04.2015 г.).
2. Приказ Министерства образования и науки Российской Федерации от 31.03.2014 г. № 253 «Об утверждении Федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования».
3. Приказ Министерства образования и науки Российской Федерации от 05.09.2013 г № 1047 «Об утверждении Порядка формирования федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования».
4. Приказ Минтруда России от 18.10.2013 г. № 544 н «Об утверждении профессионального стандарта «Педагог (педагогическая деятельность в сфере дошкольного, начального общего, основного общего, среднего общего образования) (воспитатель, учитель)» (Зарегистрировано в Минюсте России 06.12.2013 г. № 30550).
5. Приказ Минобрнауки России от 30.08.2013 г. № 1015 (ред. от 28.05.2014 г.) «Об утверждении Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам - образовательным программам начального общего, основного общего и среднего общего образования» (Зарегистрировано в Минюсте России 01.10.2013 г. № 30067)».
6. Постановление Главного государственного санитарного врача Российской Федерации от 29.12.2010 г. № 189 (ред. от 25.12.2013 г.) «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (вместе с «СанПиН 2.4.2.2821-10. Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных организациях. Санитарно-эпидемиологические правила и нормативы») (Зарегистрировано в Минюсте России 03.03.2011 г. № 19993).
7. Приказ Министерства образования и науки Российской Федерации от 14.12.2009 г. № 729 «Об утверждении перечня организаций, осуществляющих издание учебных пособий, которые допускаются к использованию в образовательном процессе в имеющих государственную аккредитацию и реализующих образовательные программы общего образования образовательных учреждениях» (Зарегистрирован Минюстом России 15.01.2010 г. № 15987).
8. Приказ Минобрнауки Российской Федерации от 13.01.2011 г. № 2 «О внесении изменений в перечень организаций, осуществляющих издание учебных пособий, которые допускаются к использованию в образовательном процессе в имеющих государственную аккредитацию и реализующих образовательные программы общего образования образовательных учреждениях» (Зарегистрировано в Минюсте РФ 08.02.2011 г. № 19739).
9. Приказ Министерства образования и науки Российской Федерации от 16.02.2012 г. № 2 «О внесении изменений в перечень организаций, осуществляющих издание учебных пособий, которые допускаются к использованию в образовательном процессе в имеющих государственную аккредитацию и реализующих образовательные программы общего образования образовательных учреждениях» (Зарегистрирован в Минюсте РФ 08.02.2011 г. № 19739).
10. Приказ Министерства образования и науки РФ от 8 декабря 2014 г. № 1559 «О внесении изменений в Порядок формирования федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования, утвержденный приказом Министерства образования и науки Российской Федерации от 5 сентября 2013 г. № 1047».
11. Приказ Минобрнауки РФ от 16.01.2012 г. № 16 «О внесении изменений в перечень организаций, осуществляющих издание учебных пособий, которые допускаются к использованию в образовательном процессе в имеющих
государственную аккредитацию и реализующих образовательные программы общего образования образовательных учреждениях» (Зарегистрировано в Минюсте Российской Федерации 17.02.2012 г. № 23251).
12. Письмо Министерства образования и науки Российской Федерации от 29.04.2014 г. № 08-548 «О федеральном перечне учебников».
Региональный уровень
1. Закон Челябинской области от 29.08.2013 г. № 515-ЗО (ред. от 28.08.2014 г.) «Об образовании в Челябинской области» (подписан Губернатором Челябинской области 30.08.2013 г.) / Постановление Законодательного Собрания Челябинской области от 29.08.2013 г. № 1543.
2. Об утверждении Концепции региональной системы оценки качества образования Челябинской области / Приказ Министерства образования и науки Челябинской области от 28.03.2013 г. № 03/961.
3. Приказ Министерства образования и науки Челябинской области от 05.12.2013 г. № 01/4591 «Об утверждении Концепции профориентационной работы образовательных организаций Челябинской области на 2013-2015 год»
4. Об утверждении Концепции развития естественно-математического и технологического образования в Челябинской области «ТЕМП» / Приказ Министерства образования и науки Челябинской области от 31.12.2014 г. № 01/3810.
Методические рекомендации
1. Методические рекомендации для руководителей образовательных организаций по реализации Федерального закона от 29.12.2012 г. № 273-ФЗ «Об образовании в Российской Федерации» / ipk74.ru/news.
2. Методические рекомендации для педагогических работников образовательных организаций по реализации Федерального закона от 29.12.2012 г. № 273-ФЗ «Об образовании в Российской Федерации» / ipk74.ru/news.
3. Информационно-методические материалы для родителей о Федеральном законе от 29.12.2012 г. № 273-ФЗ «Об образовании в Российской Федерации» / ipk74.ru/news.
4. Информационно-методические материалы о Федеральном законе от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации» для учащихся 8-11 классов / ipk74.ru/news.
Нормативные документы, обеспечивающие реализацию Федерального компонента государственного образовательного стандарта
Федеральный уровень
1. Приказ Министерства образования и науки Российской Федерации от 05.03.2004 г. № 1089 «Об утверждении Федерального компонента государственного образовательного стандарта начального общего, основного общего и среднего (полного) общего образования».
2. Приказ Министерства образования и науки Российской Федерации от 07.07.2005 г. № 03-126 «О примерных программах по учебным предметам федерального базисного учебного плана».
Региональный уровень
1. Приказ Министерства образования и науки Челябинской области от 30.05.2014 г. № 01/1839 «О внесении изменений в областной базисный учебный план для общеобразовательных организаций Челябинской области, реализующих программы основного общего и среднего общего образования».
2. Письмо от 31.07.2009 г. № 103/3404 «О разработке рабочих программ учебных курсов, предметов, дисциплин (модулей) в общеобразовательных учреждениях Челябинской области».
Методические материалы, обеспечивающие реализацию Федерального государственного образовательного стандарта общего образования и Федерального компонента государственного образовательного стандарта
1. Фундаментальное ядро содержания общего образования / под ред. В. В. Козлова, А. М. Кондакова. - М. : Просвещение, 2009.
2. Концепция духовно-нравственного развития и воспитания личности гражданина России: учебное издание / А. Я. Данилюк, А. М. Кондаков, В. А. Тишков. - М. : Просвещение, 2010.
3. Примерная основная образовательная программа образовательного учреждения. Основная школа / сост. Е. С. Савинов. М. : Просвещение, 2011.
4. Примерные программы по предмету «Математика»
Региональный уровень
1. Приказ Министерства образования и науки Челябинской области № 01-1786 от 09.06.2012 г. «О введении ФГОС основного общего образования в общеобразовательных учреждениях Челябинской области с 01 сентября 2012 г.»
2. Приказ Министерства образования и науки Челябинской области № 24/ 6142 от 20.08.2012 г. «О порядке введения ФГОС основного общего образования в общеобразовательных учреждениях с 01 сентября 2012 г.».
3. Приказ Министерства образования и науки Челябинской области № 03-02/7233 от 17 сентября 2014 г «О направлении информации по вопросам разработки и утверждения образовательных программ в общеобразовательных организациях».
4. Письмо Министерства образования и науки Челябинской области от 12.02.2014 г. № 03-02/889 «О приоритетных направлениях повышения квалификации педагогических и руководящих работников областной системы образования Челябинской области в 2014 году».
5. Письмо Министерства образования и науки Челябинской области от 09.04.2015 г. № 03-02/2789 «О проведении мониторинга в 2015 году оценки качества образования в общеобразовательных организациях Челябинской области».
6. Письмо Министерства образования и науки Челябинской области от 18.06.2011 г. № 103/4286 «О введении федерального государственного образовательного стандарта начального общего образования в образовательных учреждениях Челябинской области в 2011-2012 учебном году».
7. Письмо Министерства образования и науки Челябинской области от 01.02.2012 г. № 103/651 «О внесении изменений в основные образовательные программы начального общего образования общеобразовательных учреждений Челябинской области».
8. Письмо Министерства образования и науки Челябинской области от 02.03.2015 г. № 03-02/1464 «О внесении изменений в основные образовательные программы начального общего, основного общего, среднего общего образования общеобразовательных организаций Челябинской области».
9. Письмо Министерства образования и науки Челябинской области от 08.08.2012 г. № 24/5868 «Об особенностях повышения квалификации в условиях введения Федеральных государственных образовательных стандартов общего образования».
Методические рекомендации
1. Методические рекомендации по учету национальных, региональных и этнокультурных особенностей при разработке общеобразовательными учреждениями основных образовательных программ начального, основного, среднего общего образования / В. Н. Кеспиков, М. И. Солодкова, Е. А. Тюрина, Д. Ф. Ильясов, Ю. Ю. Баранова, В. М. Кузнецов, Н. Е. Скрипова, А. В. Кисляков, Т. В. Соловьева, Ф. А. Зуева, Л. Н. Чипышева, Е. А. Солодкова, И. В. Латыпова, Т. П. Зуева; Мин-во образования и науки Челяб. обл. ;Челяб. ин-т переподгот. и повышения квалификации работников образования. - Челябинск : ЧИППКРО, 2013. - 164 с.
Нормативное обеспечение программы:
-
.Закон об образовании РФ.
-
.Федеральный компонент государственного стандарта общего образования. Стандарт основного общего образования по математике. //Вестник образования России.2004. №12 с.107-119.
-
Обязательный минимум содержания основного общего образования по предмету. (Приказ МО от 19.05.1998 №1276)
-
Программы по геометрии к учебнику для 10-11 классов общеобразовательных школ авторов Л.С. Атанасяна, В.Ф. Бутузова, СБ. Кадомцева, Э.Г. Позняка и Л.С. Киселевой 2009.
-
Программы: Алгебра и начала математического анализа: 10-11 классы: И.И. Зубарева, А.Г. Мордкович, - «Мнемозина», 2009 г.;
-
Учебный план 2015 - 2016 уч.год.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по математике 10 класса составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования на профильном уровне и содержит в себе два предмета алгебра и начала анализа и геометрия, которые ведутся попеременно блоками. Она конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса. Настоящая рабочая программа разработана применительно к учебной программе для общеобразовательных школ, гимназий, лицеев: Математика 5-11 кл. / Г.М. Кузнецова, Н.Г. Миндюк - М.: Дрофа, 2007 г./, рекомендованной Департаментом общего среднего образования Министерства образования Российской Федерации, типовых авторских программ по алгебре и началам анализа Мордковича А.Г., геометрии Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др.
На основании примерных программ МинобрнаукиРФ, содержащих требования к минимальному объему содержания образования по алгебре и началам анализа и с учетом направленности класса реализуются программа профильного уровня.
Программа по математике составлена на основе:
1.Тематического планирования курса алгебры для 10 класса (профильный уровень)- 136 часов. Автор: Ким Н.А.
2.Тематического планирования курса геометрии для 10 класса (базовый уровень)- 68 часов. Автор: Ким Н.А.Интернет - источник:
Календарно-тематическое планирование алгебраtemaplan.ru/, temaplan.ru/?idstructure=15000
Программа составлена блоками: алгебра и начала анализа, геометрия.
Добавлены домашние задания.
Рабочая программа ориентирована на использование учебников:
1. А.Г. Мордкович, П.В. Семенов. Алгебра и начала анализа. 10 класс. Учебник
2. А.Г. Мордкович, П.В. Семенов. Алгебра и начала анализа. 10 класс. Задачник.
3. Атанасян Л.С., Бутузов В.Ф. Геометрия 10-11 класс.
Рабочая программа выполняет две основные функции:
-
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
-
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Задачи учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
В рамках указанных содержательных линий решаются следующие задачи:
-
систематизация сведений о числах; изучение новых видов числовых выражений и формул;
-
совершенствование практических навыков и вычислительной культуры; приобретение практических навыков, необходимых для повседневной жизни;
-
формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности;
-
развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений;
-
развитие воображения, способностей к математическому творчеству;
-
важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры;
-
формирование функциональной грамотности - умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты в простейших прикладных задачах.
Место предмета в базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации
На преподавание математики в 10 классе отведено 6 часов в неделю 4 алгебры + 2 геометрии, всего 204 часа в год.
Срок реализации программы - 1 учебный год.
Главной целью школьного образования является развитие ребенка как компетентной личности путем включения его в различные виды ценностной человеческой деятельности: учеба, познания, коммуникация, профессионально-трудовой выбор, личностное саморазвитие, ценностные ориентации, поиск смыслов жизнедеятельности. С этих позиций обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями. Это определило цели обучения математике:
-
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
-
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
-
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
-
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
На основании требований Государственного образовательного стандарта 2004г. в содержании рабочей программы предполагается реализовать актуальные в настоящее время компетентностный, личностно-ориентированный, деятельностный подходы, которые определяют задачи обучения:
-
приобретение математических знаний и умений;
-
овладение обобщенными способами мыслительной, творческой деятельностей;
-
освоение компетенций: учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентационной, смыслопоисковой и профессионально-трудового выбора.
Планируется использование элементов следующих педагогических технологий в преподавании предмета:
-
технологии полного усвоения;
-
технологии обучения на основе решения задач;
-
технологии обучения на основе схематичных и знаковых моделей;
-
технологии проблемного обучения.
В течение года возможны коррективы рабочей программы, связанные с объективными причинами.
Требования к уровню подготовки учащихся 10 класса
должны знать:
Корень степени n > 1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем.
Основы тригонометрии.Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций простейших тригонометрических выражений. Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Простейшие тригонометрические неравенства. Арксинус, арккосинус, арктангенс числа.
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Тригонометрические функции, их свойства и графики; периодичность, основной период.
Производная. Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков.
Параллельность прямых и плоскостей. Параллельные прямые в пространстве. Параллельность трех прямых. Параллельность прямой и плоскости. Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми. Параллельные плоскости. Свойства параллельных плоскостей. Тетраэдр.
Перпендикулярность прямых и плоскостей. Перпендикулярныепрямые в пространстве. Параллельные прямые, перпендикулярные к плоскости. Признак перпендикулярности прямой и плоскости. Теорема о прямой, перпендикулярной к плоскости. Расстояние от точки до плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Двугранный угол. Признак перпендикулярности двух плоскостей. Прямоугольный параллелепипед.
Многогранники. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Сечения куба, призмы, пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Векторы в пространстве. Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число. Компланарные вектора. Правило параллелепипеда. Разложение вектора по трем некомпланарным векторам.
должны уметь (на продуктивном уровне освоения):
Числовые и буквенные выражения
уметь
-
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
-
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
-
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
-
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
-
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
-
определять значение функции по значению аргумента при различных способах задания функции;
-
строить графики изученных функций, выполнять преобразования графиков;
-
описывать по графику и по формуле поведение и свойства функций;
-
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов;
Начала математического анализа
уметь
-
находить сумму бесконечно убывающей геометрической прогрессии;
-
вычислять производные элементарных функций, применяя правила вычисления производных, используя справочные материалы;
-
исследовать функции и строить их графики с помощью производной;
-
решать задачи с применением уравнения касательной к графику функции;
-
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа;
Уравнения и неравенства
уметь
-
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
-
доказывать несложные неравенства;
-
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;
-
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
-
находить приближенные решения уравнений и их систем, используя графический метод;
-
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
построения и исследования простейших математических моделей;
Элементы комбинаторики, статистики и теории вероятностей
уметь
-
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
-
вычислять вероятности событий на основе подсчета числа исходов (простейшие случаи);
должны уметь (на продуктивном и творческом уровнях освоения):
-
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
-
анализировать в взаимное расположение объектов в пространстве;
-
изображать основные многогранники; выполнять чертежи по условиям задач;
-
строить простейшие сечения куба, призмы, пирамиды;
-
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей);
-
использовать при решении стереометрических задач планиметрические факты и методы;
-
проводить доказательные рассуждения в ходе решения задач;
Способны использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
-
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
-
вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет - ресурсов:
-
Министерство образования РФ:
www.ed.gov.ru/;
www.edu.ru/
-
Тестирование online: 5 - 11 классы:
www.kokch.kts.ru/cdo/
-
Педагогическая мастерская, уроки в Интернет и многое другое:
www.proshkolu.ru/
www.uchportal.ru/
-
Мегаэнциклопедия Кирилла и Мефодия:
mega.km.ru
-
сайты «Энциклопедий энциклопедий», например:
www.rubricon.ru/;
www.encyclopedia.ru
УЧЕБНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
10 класс
Содержание программы
Алгебры и начала математического анализа
Повторение материала 7-9 классов (4ч)
-
Действительные числа (12ч)
Натуральные и целые числа. Делимость чисел. Основная теорема арифметики натуральных чисел. Рациональные, иррациональные, действительные числа, числовая прямая. Числовые неравенства. Аксиоматика действительных чисел. Модуль действительного числа. Метод математической индукции.
-
Числовые функции (10ч)
Определение числовой функции, способы ее задания, свойства функций. Периодические и обратные функции.
-
Тригонометрические функции (23ч)
Числовая окружность на координатной плоскости. Синус и косинус. Тангенс и котангенс. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента, их свойства и графики. Сжатие и растяжение графиков тригонометрических функций. Обратные тригонометрические функции.
-
Тригонометрические уравнения и неравенства (10ч)
Простейшие тригонометрические уравнения и неравенства. Методы решения тригонометрических уравнений: введение новой переменной, разложение на множители, однородные тригонометрические уравнения.
-
Преобразование тригонометрических выражений (22ч)
Формулы сложения, приведения, двойного аргумента, понижения степени. Преобразование суммы тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы. Методы решения тригонометрических уравнений (продолжение).
-
Комплексные числа (9ч)
Комплексные числа и арифметические операции над ними. Комплексные числа и координатная плоскость. Тригонометрическая форма записи комплексного числа. Комплексные числа и квадратные уравнения. Возведение комплексного числа в степень. Извлечение квадратного и кубического корня из комплексного числа.
-
Производная (29ч)
Определение числовой последовательности и способы ее задания. Свойства числовых последовательностей.
Определение предела последовательности. Свойства сходящихся последовательностей. Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии.
Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции.
Задачи, приводящие к понятию производной. Определение производной. Алгоритм отыскания производной. Формулы дифференцирования. Правила дифференцирования. Понятие производной n-го порядка. Дифференцирование сложной функции. Дифференцирование обратной функции. Уравнение касательной к графику функции. Алгоритм составления уравнения касательной к графику функции y = f(x).
Применение производной для доказательства тождеств и неравенств. Построение графиков функций. Применение производной для отыскания наибольших и наименьших значений непрерывной функции на промежутке. Задачи на оптимизацию.
-
Комбинаторика и вероятность (7ч).
Правило умножения. Перестановки и факториалы. Выбор нескольких элементов. Сочетания и размещения. Бином Ньютона. Случайные события и их вероятности.
Геометрия
-
Аксиомы стереометрии.(2ч).
Предмет стереометрии. Аксиомы стереометрии. Некоторые следствия из аксиом.
-
Параллельность прямых и плоскостей (20ч).
Параллельность прямых, прямой и плоскости. Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми. Параллельность плоскостей. Тетраэдр и параллелепипед.
-
Перпендикулярность прямых и плоскостей (20ч).
Перпендикулярность прямой и плоскости. Перпендикуляр и наклонные. Угол между прямой и плоскостью. Двугранный угол. Перпендикулярность плоскостей. Трехгранный угол. Многогранный угол. Перпендикулярность плоскостей.
Основная цель - ввести понятия перпендикулярности прямых и плоскостей, изучить признаки перпендикулярности прямой и плоскости, двух плоскостей.
-
Многогранники (14ч).
Понятие многогранника. Геометрическое тело. Теорема Эйлера. Призма. Пространственная теорема Пифагора. Пирамида. Правильные многогранники.
Основная цель - познакомить учащихся с основными видами многогранников (призма, пирамида, усеченная пирамида), с формулой Эйлера для выпуклых многогранников, с правильными многогранниками и элементами их симметрии.
-
Некоторые сведения из планиметрии. (4 ч).
Теоремы Менелая и Чевы. Эллипс, гипербола и парабола.
Требования к уровню подготовки учащихся
В результате изучения математики на профильном уровне ученик должен знать/понимать:
-
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
-
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа;
-
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
-
вероятностный характер различных процессов окружающего мира;
-
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе.
-
использовать приобретённые знания и умения в практической деятельности и повседневной жизни.
Тема: Числовые и буквенные выражения. Начала математического анализа.
Учащийся должен уметь:
-
выполнять арифметические действия, сочетая устные и письменные приёмы, применение вычислительных устройств; находить значение корня натуральной степени, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчётах; выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами.
-
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени и тригонометрические функции;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально-экономических и физических - на наибольшее и наименьшее значения, на нахождение скорости и ускорения.
Тема: Уравнения и неравенства
Учащийся должен уметь:
-
решать тригонометрические уравнения и их системы;
-
составлять уравнения и неравенства по условию задачи;
-
использовать для приближенного решения уравнений и неравенств графический метод;
-
изображать на координатной плоскости множества решений простейших уравнений и их систем.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших математических моделей.
Тема: Функции и графики
Учащийся должен уметь:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшее и наименьшее значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для описания с помощью функций различных зависимостей, представления их графически, для интерпретации графиков.
Тема:Элементы комбинаторики
Учащийся должен уметь:
-
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля
-
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков.
Требования к математической подготовке учащихсяпо геометрии
-
Уметь решать простые задачи по всем изученным темам, выполняя стереометрический чертеж.
-
Уметь описывать взаимное расположение прямых и плоскостей в пространстве.
-
Уметь анализировать в простейших случаях взаимное расположение объектов в пространстве.
-
Уметь изображать основные многоугольники; выполнять чертежи по условию задач.
-
Уметь строить простейшие сечения куба, призмы, пирамиды.
-
Уметь решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей).
-
Уметь использовать при решении стереометрических задач планиметрические факты и методы.
-
Уметь распознавать на чертежах и моделях пространственные формы.
-
Уметь описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении.
-
Проводить доказательные рассуждения в ходе решения задач.
-
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: исследования (моделирования) практических ситуаций на основе изученных формул и свойств фигур; вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Тематическое планирование курса математики для 10 класса (профильный уровень)-136 часов из них 4 часа алгебры ( 34 учебных недель)
Рабочая программа ориентирована на использование учебников:
1. А.Г. Мордкович, П.В. Семенов. Алгебра и начала анализа. 10 класс. Учебник
2. А.Г. Мордкович, П.В. Семенов. Алгебра и начала анализа. 10 класс. Задачник.
3. Атанасян Л.С., Бутузов В.Ф. Геометрия 10-11 класс.
Общеучебные цели:
-
Создание условия для умения логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки.
-
Создание условия для умения ясно, точно и грамотно выражать свои мысли в устной и письменной речи.
-
Формирование умение использовать различные языки математики: словесный, символический, графический.
-
Формирование умение свободно переходить с языка на язык для иллюстрации, интерпретации, аргументации и доказательства.
-
Создание условия для плодотворного участия в работе в группе; умения самостоятельно и мотивированно организовывать свою деятельность.
-
Формирование умение использовать приобретенные знания и умения в практическойдеятельности и повседневной жизнидля исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств тел; вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Создание условия для интегрирования в личный опыт новой, в том числе самостоятельно полученной информации.
Общепредметные цели:
-
Формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов.
-
Овладение устным и письменным математическим языком, математическим знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне.
-
Развитее логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности.
Воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
|
Повторение курса 9 класса (4
ч)
|
| |||||||||||||
|
сентябрь |
Тема: Упрощение рациональных выражений (1 ч). |
| ||||||||||||
|
Цели урока:повторение с учащимися действий с дробями, используя формулы сокращенного умножения; закрепление навыков учащихся в доказательстве рациональных тождеств. | ||||||||||||||
|
1 |
Поисковая |
Проблемные задания, фронтальный опрос, упражнения |
Индивидуальная. Решение качественных задач. |
Знают формулы сокращенного умножения; могут сокращать дроби и выполнять все действия с дробями. Используют для решения познавательных задач справочную литературу. (П) |
Умеют доказывать рациональные тождества и упрощать выражения, применяя формулы сокращенного умножения. Умеют передавать, информацию сжато, полно, выборочно. (ТВ) |
Использование мультимедийных ресурсов и компьютерных технологий для создания базы данных. |
П. 7(в,г), П.10(в,г) |
| ||||||
|
|
Тема: Решение уравнений (1 ч). |
| ||||||||||||
|
Цели урока:повторение с учащимися методов решения уравнений; обобщение и систематизация сведений учащихся о решении уравнений. | ||||||||||||||
|
2 |
Поисковая |
Проблемные задания, фронтальный опрос, упражнения |
Индивидуальная. Решение упражнений, составление опорного конспекта, ответы на вопросы. |
Знают, как: решать рациональные, квадратные уравнения и простейшие иррациональные; составлять уравнения по условию задачи; использовать для приближенного решения уравнений графический метод (П) |
Умеют решать рациональные, квадратные уравнения. Умеют решать иррациональных уравнений.Знают основные приемы решения уравнений: подстановка, введение новых переменных. Понимают равносильность уравнений (ТВ), |
Самостоятельное составление алгоритмических предписаний и инструкций по теме |
П.24 (в,г), П.25(в,г) |
| ||||||
|
|
Тема: Решение неравенств (1 ч). |
| ||||||||||||
|
Цели урока:повторение с учащимися методов решения неравенств; обобщение и систематизация сведений учащихся о решении неравенств. | ||||||||||||||
|
3 |
Комбинированная |
Практикум, фронтальный опрос |
Индивидуальная. Построение алгоритма действия, решение упражнений, |
Учащиеся знают о решении рациональных, квадратных неравенств и простейших иррациональных. Могут составлять неравенства по условию задачи; использовать для приближенного решения неравенств графический метод. (П). |
Умеют решать рациональные, квадратные, иррациональные неравенства. Используют метод интервалов. Знают равносильность неравенств. Могут изображать на координатной плоскости множества решений простейших неравенств . |
Использование мультимедийных ресурсов и компьютерных технологий для создания базы данных. |
П.30(в,г), П.33(в,г) |
| ||||||
|
|
Вводный контроль (1 ч). |
| ||||||||||||
|
Цель урока проверить знания и умение учащихся по темам 9-го класса: Упрощение рациональных выражений; Решение уравнений; Решение неравенств. | ||||||||||||||
|
4 |
Урок обобщения и систематизации знаний |
Самостоятельное планирование и проведение исследования решения |
Индивидуальное решение контрольных заданий. |
Учащихся демонстрируют умение обобщения и систематизации знаний по основным темам курса математики 9 класса. (П) |
Учащиеся могут свободно пользоваться умением обобщения и систематизации знаний по задачам повышенной сложности. (ТВ) |
Владеют навыками самоанализа и самоконтроля |
4, 5 |
| ||||||
Действительные числа (12 ч )
Основные цели: создать условия учащимся для:
-
Формулирования понимания признаков делимости, деление с остатком, аксиоматики действительных чисел, основной теоремой арифметики.
-
Овладение умением применение метода математической индукции для доказательства утверждений и числовых неравенств.
Тема: Натуральные и целые числа (3 ч).
Цели урока: формулирование понимания учащихся о свойствах и признаках делимости натуральных чисел; формирование учащимися умения определять простые и составные числа; овладение умением доказывать и применять основную теорему арифметики.
5
Поисковая
Организация совместной учебной деятельности
Групповая, Работа с конспектом, с книгой и наглядными пособиями.
Имеют представление с свойствах и признаках делимости натуральных чисел; могут определить простые и составные числа. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах (Р)
Могут применять свойства и признаки делимости натуральных чисел. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (И)
Построение и исследования математических моделей для описания и решения задач из смежных дисциплин.
§1, №7,8,12
6
Поисковая
Проблемные задания, индивидуальный опрос
Групповая, индивидуальная. Решение качественных задач.
Знают теорему о делении с остатком; основную теорему арифметики натуральных чисел. Умеют работать с учебником, отбирать и структурировать материал. (П)
Могут применять теорему о делении с остатком; основную теорему арифметики натуральных чисел. Умеют извлекать необходимую информацию из учебно-научных текстов. (И)
Осуществляют самостоятельный поиск информации в различных источниках
§1, №26(а,г)35(б,в), 39(а)
7
Комбинированная
Практикум, фронтальный опрос
Индивидуальная, составление опорного конспекта и работа с ним.
Знают теорему о делении с остатком; основную теорему арифметики натуральных чисел. Могут привести примеры, подобрать аргументы, сформулировать выводы. (П)
Могут применять теорему о делении с остатком; основную теорему арифметики натуральных чисел. Умеют, развернуто обосновывать суждения. (ТВ)
Поиск нужной информации по заданной теме в источниках различного типа.
§1, №43, 51-54
Тема: Рациональные числа (1ч).
Цели урока: формирование представлений учащихся о рациональных числах и бесконечных десятичных периодических числах; овладение учащимися умением любое рациональное число записать в виде конечной десятичной дроби и наоборот.
8
Проблемное изложение
Проблемные задачи, опрос, упражнения
Фронтальная, групповая Работа с наглядными пособиями.
Знают понятие рациональные числа, бесконечная десятичная периодическая дробь. Умеют определять понятия, приводить доказательства. (Р)
Могут любое рациональное число записать в виде конечной десятичной дроби и наоборот. Умеют передавать, информацию сжато, полно,
Анализ условий задач, составле-ниематематич. модели
§2, №13(б,в), 15, 16
Тема: Иррациональные числа (2 ч).
Цели урока: формирование представлений учащихся о понятие иррационального числа; овладение учащимися умением доказать иррациональность числа.
9
Объяснительно-иллюстративная
Лекция, работа с книгой
Фронтальная, работа с дополнительным материалом
Имеют представление о понятие иррациональное число. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах (Р)
Могут доказать иррациональность числа. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (И)
Проведение доказательных рассуждений, логического обоснования выводов
§3, №5, 6, 9
10
Проблемное изложение
Проблемные задачи, индивидуальный опрос
Групповая Работа с конспектом, с книгой.
Знают понятие иррациональное число. Используют для решения познавательных задач справочную литературу. (П)
Могут доказать иррациональность числа. Умеют работать с учебником, отбирать и структурировать материал. (ТВ)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§3, №14-16
Тема: Множество действительных чисел (1 ч).
Цели урока: формирование представлений учащихся о делимости целых чисел, о деление с остатком; овладение учащимися умением решать задачи с целочисленными неизвестными.
11
Объяснительно-иллюстративная
Практикум, фронтальный опрос
демонстрация слайд - лекции
Фронтальная.
Составление опорного конспекта, ответы на вопросы.
Знают о делимости целых чисел; о деление с остатком. Может решать задачи с целочисленными неизвестными. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (Р)
Знают о делимости целых чисел; о деление с остатком. Может решать задачи с целочисленными неизвестными. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Построение математических моделей для описания и решения прикладных задач.
§4, №14(в,г), 15, 17
Тема: Модуль действительного числа (2 ч).
Цели урока: формирование представлений учащихся об определении модуля действительного; овладение учащимися умением доказывать свойства модуля и решать модульные неравенства.
12
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Групповая, индивидуальная, работа с демонстрационным материалом,
Имеют представление об определении модуля действительного; могут применять свойства модуля. Умеют составлять текст научного стиля. Могут критически оценить информацию адекватно поставленной цели. (Р)
Могут доказывать свойства модуля и решать модульные неравенства. Могут составить набор карточек с заданиями. Умеют использовать элементы причинно-следственного и структурно-функционального анализа. (И)
Умеют извлекать необходимую информацию из учебно-научных текстов
§5, №11, 13,(в,г,)
13
Объяснительно-иллюстративная
Проблемные задания, работа с книгой
Индивидуальная. Построение алгоритма действия, решение упражнений.
Знают определение модуля действительного; могут применять свойства модуля. Умеют, развернуто обосновывать суждения. (П)
Могут доказывать свойства модуля и решать модульные неравенства. Умеют определять понятия, приводить доказательства. (ТВ)
§5, №14(а), 16, 22
Тема: Метод математической индукции (2 ч).
Цели урока: формирование представлений учащихся о методе математической индукции; овладение учащимися умением доказывать тождество и неравенство методом математической индукции.
14
Объяснительно-иллюстративная
Проблемные задания, работа с книгой
Фронтальная.
Построение алгоритма действия, решение упражнений.
Знают, как применять метод математической индукции при доказательстве числовых тождеств и неравенств. Умеют, развернуто обосновывать суждения. Умеют решать проблемные задачи и ситуации (Р)
Свободно используют метод математической индукции при доказательстве числовых тождеств и неравенств. Умеют извлекать необходимую информацию из учебно-научных текстов. (И)
Решение широкого класса задач из различных разделов курса
§6, №2, 3(в,г)
15
Проблемное изложение
Проблемные задачи, индивидуальный опрос
Групповая, индивидуальная. Составление опорного конспекта, решение задач.
Могут обосновано применять метод математической индукции при доказательстве числовых тождеств и неравенств. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Могут доказать любое тождество и неравенство методом математической индукции. Используют для решения познавательных задач справочную литературу. (ТВ)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§6, №2, 3(в,г)
Контрольная работа №1
Цель урока проверить знания и умение учащихся по теме действительные числа.
16
Урок контроля, оценки и коррекции знаний
Самостоятельное планирование и проведение исследования решения
Индивидуальное решение контрольных заданий.
Учащихся демонстрируют: понимание признаков делимости; умение делить с остатком; знание аксиоматики действительных чисел и основнойтеоремой арифметики.
Учащиеся могут свободно пользоваться методом математической индукции при доказательстве равенств. Владеют навыками самоанализа и самоконтроля
Владеют навыками самоанализа и самоконтроля
4, 5
проблемные дифференцированные задания.
Числовые функции (9 ч).
Основные цели: создать условия учащимся для:
-
Формирования понимания числовой функции, ее свойств: монотонность, ограниченность сверху и снизу, максимумом и минимумом; четность и нечетность; периодичность; обратная функция.
-
Овладение умением описывать по графику и по формуле поведение и свойства функции.
Тема: Определение числовой функции и способы ее задания (2 ч).
Цели урока: формирование представлений учащихся о числовой функции; овладение учащимися умением строить кусочно-заданная функцию, функцию дробной части числа, функцию целой части числа.
17
Объяснительно-иллюстративная
Лекция, демонстрация
Фронтальная.
Решение упражнений, составление опорного конспекта
Знают понятие числовой функции; могут строить кусочно-заданная функцию, функцию дробной части числа, функцию целой части числа. Умеют передавать, информацию сжато, полно, выборочно (Р)
Могут строить кусочно-заданная функцию, функцию дробной части числа, функцию целой части числа. Умеют определять понятия, приводить доказательства. (И)
Поиск нужной информации в различных источниках
§7, №22-24(а,б),27
18
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Групповая, индивидуальная, работа с демонстрационным материалом,
Знают понятие числовой функции; могут строить кусочно-заданную функцию, функцию дробной части числа, функцию целой части числа. Могут составить набор карточек с заданиями (П)
Могут строить кусочно-заданную функцию, функцию дробной части числа, функцию целой части числа. Умеют находить и использовать информацию. (ТВ)
Самостоятельно искать, извлекать и отбирать необходимую для решения задач информац
§7, №28(а,б), 31-32(а), №29(а,в)
Тема: Свойства функции (3 ч).
Цели урока: формирование представлений учащихся о свойствах функции: монотонности, наибольшем и наименьшем значении функции, ограниченности, выпуклости и непрерывности; овладение учащимися умением свободно использовать для построения графика функции свойства функции; формирование умения исследовать функцию на монотонность, определяют наибольшее и наименьшее значение функции, ограниченность, выпуклость.
19
Объяснительно-иллюстративная
Проблемные задачи, решение качественных заданий
Фронтальная.
Составление опорного конспекта, решение задач, работа с тестом
Имеют представление о свойствах функции: монотонности, наибольшем и наименьшем значении функции, ограниченности, выпуклости и непрерывности. Умеют, развернуто обосновывать суждения. (Р)
Могут свободно использовать для построения графика функции свойства функции: монотонность, наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность.. (И)
Поисковая и деятельность при решении задач повышенной сложности и нетиповых задач.
§8,№2(а,б), 3(а), 18(а,б), 34(а,в)
20
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Групповая, индивидуальная. Решение упражнений,
Могут исследовать функции на: монотонность, наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность. Умеют отбирать и структурировать материал (П)
Могут свободно исследовать функцию на монотонность, определяют наибольшее и наименьшее значение функции, ограниченность, выпуклость. (И)
Использование справочной литературы, а также материалов ЕГЭ
§8, №2(в,г), 3(г), 44, 34(б,г)
21
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная. Решение упражнений, ответы на вопросы.
Могут исследовать функции на: монотонность, наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность. Могут собрать материал для сообщения по заданной теме. Могут критически оценить информацию адекватно поставленной цели. (П)
Могут свободно исследовать функцию на монотонность, определяют наибольшее и наименьшее значение функции, ограниченность, выпуклость. Умеют определять понятия, приводить доказательства.
Построения и исследования математических моделей для решения прикладных задач
§8, №39, 45
Тема: Периодические функции (1 ч).
Цели урока: формирование представлений учащихся о периодичности функции, об основном периоде; овладение учащимися умением определять период функции и строить их графики.
22
Проблемное изложение
Практикум, фронтальный опрос
демонстрация слайд - лекции
Фронтальная.
работа с конспектом, работа с книгой и наглядными пособиями.
Знают о периодичности функции, об основном периоде. Умеют извлекать необходимую информацию из учебно-научных текстов. (Р)
Могут определять период функции и строить их графики. Могут привести примеры, подобрать аргументы, сформулировать выводы. (П)
Приобретают умения включение своих результатов в результаты работы группы
§9, №8, 24, 25
Тема: Обратная функция (2 ч).
Цели урока: формирование представлений учащихся об обратимости функции; овладение учащимися умением свободно строить функции обратные данной.
23
Поисковая
проблемные задания, фронтальный опрос, упражнения
Групповая, индивидуальная. Составление опорного конспекта, решение задач.
Понимают об обратимости функции и могут строить функции обратные данной. Могут собрать материал для сообщения по заданной теме. (Р)
Понимают об обратимости функции и могут строить функции обратные данной. Используют для решения познавательных задач справочную литературу. (И)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§10,№7(б,г),9(а), 11, 13(а)
24
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная. Работа с демонстрационным материалом,
Понимают об обратимости функции и могут строить функции обратные данной. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Понимают об обратимости функции и могут строить функции обратные данной. Умеют определять понятия, приводить доказательства. (ТВ)
Поиск нужной информации по заданной теме в источниках различного типа.
§10, №18, 26(а)
Контрольная работа №2
Цель урока проверить знания и умение учащихся по теме числовые функции.
25
Урок контроля, оценки и коррекции знаний
Самостоятельное планирование и проведение исследования решения
Индивидуальное решение контрольных заданий.
Учащихся демонстрируют: умение работать с числовыми функциями, используя их свойства: монотонность, ограниченность сверху и снизу, максимум и минимум, четность и нечетность, периодичность, с обратной функцией. (П)
Учащиеся могут свободно использовать свойства функций для описания функциональной зависимости. Владеют навыками самоанализа и самоконтроля. (ТВ)
Владеют навыками самоанализа и самоконтроля
4, 5
проблемные дифференцированные задания.
Тригонометрические функции (24 ч).
Основные цели: создать условия учащимся для:
-
Расширения и обобщения сведений о числовой окружности на координатной плоскости.
-
Формирования умения находить значение синуса, косинуса, тангенса и котангенса на числовой окружности.
-
Формирования представления понятия тригонометрической функции числового и углового аргумента.
Тема: Числовая окружность (2ч).
Цели урока:формирование представления понятия числовой окружности у учащихся; формирование умения учащихся записывать множество чисел, соответствующих на числовой окружности точке; овладение умением учащихся находить на числовой окружности точку, соответствующую данному числу.
26
Поисковая
Прохождение материала быстрым темпом
Фронтальная, индивидуальная. Построение алгоритма действия, решение упражнений.
Имеют представление, как можно на единичной окружности определять длины дуг. Могут найти на числовой окружности точку соответствующую данному числу. Умеют приводить примеры, подбирают аргументы, формулируют выводы. (Р)
Могут, используя числовую окружность, находить все числа, которым на числовой окружности соответствуют точки, принадлежащие дугам. Могут записать формулу бесконечного числа точек. Могут критически оценить информацию адекватно поставленной цели. (И)
Поиск нужной информации по заданной теме в источниках различного типа.
§1; §11 № 11,18, 19 (а), 22(а,б)
27
Комбинированная
Практикум, фронтальный опрос, упражнения
Групповая, работа с демонстрационным материалом
Знают, как можно на единичной окружности определять длины дуг. Могут найти на числовой окружности точку соответствующую данному числу. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Могут, используя числовую окружность, находить все числа, которым на числовой окружности соответствуют точки, принадлежащие дугам. Могут записать формулу бесконечного числа точек (ТВ)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§1; §11 № 32-34 (а,б)
Тема: Числовая окружность на координатной плоскости (2ч).
Цели урока:формирование представление учащихся о понятии числовой окружности на координатной плоскости; составление учащимися таблицы значений координат точек числовой окружности; закрепить умение учащихся находить на числовой окружности точки с конкретным значением абсциссы и ординаты, а также умением определить каким числам они соответствуют
28
Поисковая
Проблемные задания, индивидуальный опрос
Фронтальная, индивидуальная. Составление опорного конспекта, решение задач, работа с тестом и книгой
Имеют представление, как определить координаты точек числовой окружности. Могут составить таблицу для точек числовой окружности и их координат. Могут по координатам находить точку числовой окружности. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (Р)
Могут определять точку числовой окружности по координатам и координаты по точке числовой окружности. Могут находить точки, координаты которых удовлетворяют заданному неравенству. Умеют использовать элементы причинно-следственного и структурно-функционального анализа. (И)
Построения и исследования математических моделей для описания и решения прикладных задач
§2; §12 № 2, 3, 6 (а,б), 9
29
Комбинированная
Практикум, фронтальный опрос, упражнения
Индивидуальная. Построение алгоритма действия, решение упражнений,
Знают, как определить координаты точек числовой окружности. Могут составить таблицу для точек числовой окружности и их координат. Могут по координатам находить точку числовой окружности. Умеют обосновывать суждения. Умеют отбирать и структурировать материал (П)
Могут определять точку числовой окружности по координатам и координаты по точке числовой окружности. Могут находить точки, координаты которых удовлетворяют заданному неравенству. Могут самостоятельно отбирать информаци
Составление обобщающих информационных таблиц (конспектов)
§2; §12 № 14-18(б), 21-24(б)
Тема: Синус, косинус. Тангенс, котангенс (3ч).
Цели урока:формирование представления учащихся о понятие синуса, косинуса, тангенса и котангенса; составление учащимися таблицы их значений; формирование умения использовать свойства тригонометрических функций.
30
Объяснительно-иллюстративная
Фронтальный опрос
демонстрация слайд - лекции
Фронтальная, групповая фронтальная работа с конспектом, работа с книгой и наглядными пособиями.
Знают понятие синус, косинус, тангенс, котангенс произвольного угла; радианную меру угла; могут вычислить синус, косинус, тангенс и котангенс числа. Могут вывести некоторые свойства синуса, косинуса, тангенса. (Р)
Могут, используя числовую окружность определять синус, косинус, тангенс, котангенс произвольного угла в радианной и градусной мере. Могут решать простейшие уравнения и неравенства. (И)
Приобретают умения самостоятельной и коллективной деятельности.
§3; §13 № 4(а,б), 5 (а), 6(а,б), 8, 9
31
Поисковая
Проблемные задания, фронтальный опрос, упражнения
Групповая. Построение алгоритма действия, решение упражнений, ответы на вопросы.
Знают понятие синус, косинус, тангенс, котангенс произвольного угла; радианную меру угла; могут вычислить синус, косинус, тангенс и котангенс числа. Могут вывести некоторые свойства синуса, косинуса, тангенса. (П)
Могут, используя числовую окружность определять синус, косинус, тангенс, котангенс произвольного угла в радианной и градусной мере. Могут решать простейшие уравнения и неравенства. (И)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§3; §13 № 14(а), 22, 23, 41(а)
32
Комбинированная
Практикум, фронтальный опрос, упражнения
Индивидуальная, работа с демонстрационным материалом.
Знают понятие синус, косинус, тангенс, котангенс произвольного угла; радианную меру угла; могут вычислить синус, косинус, тангенс и котангенс числа. Могут вывести некоторые свойства синуса, косинуса, тангенса. (П)
Могут, используя числовую окружность определять синус, косинус, тангенс, котангенс произвольного угла в радианной и градусной мере. Могут решать простейшие уравнения и неравенства. (ТВ)
Использование различной литературы для создания презентации своего проекта обобщения материала
§3; §13 № 27-30 (а,б), 31(а,б). 32, 42(а)
Тема: Тригонометрические функции числового аргумента (2ч).
Цели урока:формирование представления учащихся о тригонометрической функции числового аргумента; формирование учащихся умения вывести основные формулы одного аргумента тригонометрических функций; формирование умения учащихся упрощать выражения с применением основных формул одного аргумента тригонометрических функций; развитие навыков упрощение выражений с применением основных формул одного аргумента тригонометрических функций.
33
Комбинированная
Прохождение материала быстрым темпом
Индивидуальная. Построение алгоритма действия, решение упражнений.
Зная основные тригонометрические тождества, могут совершать преобразования простых тригонометрических выражений (Р)
Зная основные тригонометрические тождества, могут совершать преобразования сложных тригонометрических выражений (И)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§4; §14 № 4-6(а,б), 14-15(б)
34
Поисковая
Практикум, индивидуальный опрос
Индивидуальная. Работа с опорными конспектами, работа с раздаточными материалами
Зная основные тригонометрические тождества, могут совершать преобразования простых тригонометрических выражений. Умеют составлять текст научного стиля (П)
Зная основные тригонометрические тождества, могут совершать преобразования сложных тригонометрических выражений. Могут собрать материал для сообщения по заданной теме (ТВ)
Использование справочной литературы, а также материалов ЕГЭ
§4; §14 № 8-9(а,б), 11-13(г)
Тема: Тригонометрические функции углового аргумента (1ч).
Цели урока: формирование представления учащихся о тригонометрической функции углового аргумента, понятие радианной меры угла; формирование умение учащихся переводить радианную меру угла в градусную и наоборот; овладение умением учащихся вычислять значения синуса, косинуса, тангенса и котангенса градусной и радианной меры угла, используя табличные значения.
35
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Фронтальная, индивидуальная
Знают, как вычислять значения синуса, косинуса, тангенса и котангенса градусной и радианной меры угла, используя табличные значения. Знают формулы перевода градусной меры в радианную меру и наоборот. (Р)
Умеют вычислять значения синуса, косинуса, тангенса и котангенса градусной и радианной меры угла, используя табличные значения. Умеют применять формулы перевода градусной меры в радианную меру и наоборот. (П)
Объяснение изученных положений на самостоятельно подобранных конкретных примерах
§5; §15 № № 1-6 (а,б), 14
Тема: Функции ![]() ,
, ![]() ее свойства и
графики (3ч).
ее свойства и
графики (3ч).
Цели урока:формирование представления учащихся о
тригонометрических функциях ![]() ,
, ![]() , их свойствах; формирование
умения учащихся совершать преобразования графиков
функций
, их свойствах; формирование
умения учащихся совершать преобразования графиков
функций![]() ,
,
![]() , зная
их свойства; овладение умением учащихся свободно строить
графики функций повышенной сложности и описывать их свойства.
, зная
их свойства; овладение умением учащихся свободно строить
графики функций повышенной сложности и описывать их свойства.
36
Проблемное изложение
Практикум, фронтальный опрос
демонстрация слайд - лекции
Фронтальная, индивидуальная, работа с демонстрационным материалом,
Имеют представление о тригонометрических функциях ![]() ,
, ![]() , их свойствах. Могут
объяснить изученные положения на подобранных конкретных примерах.
Умеют проводить самооценку собственных действий. (Р)
, их свойствах. Могут
объяснить изученные положения на подобранных конкретных примерах.
Умеют проводить самооценку собственных действий. (Р)
Могут совершать преобразования графиков функций ![]() ,
, ![]() Умеют отбирать и
структурировать материал. Умеют извлекать необходимую информацию
из учебно-научных текстов. (И)
Умеют отбирать и
структурировать материал. Умеют извлекать необходимую информацию
из учебно-научных текстов. (И)
Приобретают умения самостоятельной и коллективной деятельности.
§7; № 1(а,б), 5(а,б), 8(а,б), 11(а,б),
37
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная. Построение алгоритма действия, решение упражнений.
Могут рассматривать в сравнении тригонометрические функции
![]() ,
, ![]() , их свойства и могут
строить графики. Могут собрать материал для сообщения по заданной
теме. (П)
, их свойства и могут
строить графики. Могут собрать материал для сообщения по заданной
теме. (П)
Могут совершать преобразования графиков функций![]() ,
, ![]() , зная их
свойства; могут решать графически уравнения. Умеют составлять
текст научного стиля (И)
, зная их
свойства; могут решать графически уравнения. Умеют составлять
текст научного стиля (И)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§8; §16 № 7(а,б), 9 (а,б), 33(а,б)
38
Поисковая
Организация совместной учебной деятельности
Групповая, индивидуальная, работа с опорными конспектами, работа с раздаточными материалами
Имеют представление об исследовании функции на чётность и нечётность, о нахождении области определения, область значения функции. Умеют извлекать необходимую информацию из учебно-научных текстов. Умеют проводить самооценку собственных действий. (П)
Могут свободно строить графики функций повышенной сложности и описывать их свойства. Умеют приводить примеры, подбирают аргументы, формулируют выводы. Умеют передавать, информацию сжато, полно, выборочно. (ТВ)
Проверка и оценка результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом.
§16, №20, 22, 25
Контрольная работа №4
Цель урока проверить знания и умение учащихся по теме тригонометрические функции числового и углового аргумента.
39
Урок контроля, оценки и коррекции знаний
Самостоятельное планирование и проведение исследования решения
Индивидуальное решение контрольных заданий.
Учащихся демонстрируют знания о числовой окружности на координатной плоскости; умение вычислять значение синуса, косинуса, тангенса и котангенса на числовой окружности; умение вычислять понятие тригонометрической функции числового и углового аргумента
Могут совершать преобразования графиков функций![]() ,
, ![]() , зная их
свойства; могут решать графически уравнения. Владеют навыками
самоанализа и самоконтроля. Умеют, развернуто обосновывать
суждения. (ТВ)
, зная их
свойства; могут решать графически уравнения. Владеют навыками
самоанализа и самоконтроля. Умеют, развернуто обосновывать
суждения. (ТВ)
Владеют навыками самоанализа и самоконтроля
4, 5
проблемные дифференцированные
(2ч).
Цели урока:формирование представления учащихся о
преобразовании графика функции; формирование умения
учащихся вытянуть и сжать график ![]() от оси
от оси ![]() , в зависимости от
значения
, в зависимости от
значения ![]() ;
овладение умением учащихся свободно строить графики
функций
;
овладение умением учащихся свободно строить графики
функций ![]() ,
знаяграфик
,
знаяграфик![]() и описывать их свойства.
и описывать их свойства.
40
Поисковая
Проблемные задания, фронтальный опрос, упражнения
Групповая, индивидуальная, работа с раздаточными материалами
Могут график ![]() вытянуть и сжать от оси
вытянуть и сжать от оси
![]() , в зависимости
от значения
, в зависимости
от значения ![]() .
Умеют объяснить изученные положения на самостоятельно подобранных
конкретных примерах. (Р)
.
Умеют объяснить изученные положения на самостоятельно подобранных
конкретных примерах. (Р)
Могут график ![]() вытянуть и сжать от оси
вытянуть и сжать от оси
![]() , в зависимости
от значения
, в зависимости
от значения ![]() .
Умеют извлекать необходимую информацию из учебно-научных текстов.
(И)
.
Умеют извлекать необходимую информацию из учебно-научных текстов.
(И)
Использование справочной литературы, а также материалов ЕГЭ
§8; §16 № 7(а,б), 9 (а,б), 33(а,б)
41
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная. Построение алгоритма решения упражнений.
Могут график ![]() вытянуть и сжать от оси
вытянуть и сжать от оси
![]() , в зависимости
от значения
, в зависимости
от значения ![]() .
Могут привести примеры, подобрать аргументы, сформулировать
выводы. (П)
.
Могут привести примеры, подобрать аргументы, сформулировать
выводы. (П)
Могут график ![]() вытянуть и сжать от оси
вытянуть и сжать от оси
![]() , в зависимости
от значения
, в зависимости
от значения ![]() .
Могут объяснить изученные положения на самостоятельно подобранных
конкретных примерах. (ТВ)
.
Могут объяснить изученные положения на самостоятельно подобранных
конкретных примерах. (ТВ)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информации
§16, №20, 22, 25
Тема: Построение графика функции
![]() (2ч).
(2ч).
Цели урока:формирование представления учащихся о
преобразовании графика функции; формирование умения
учащихся вытянуть и сжать график ![]() от оси
от оси ![]() , в зависимости от
значения
, в зависимости от
значения ![]() ;
овладение умением учащихся свободно строить графики
функций
;
овладение умением учащихся свободно строить графики
функций ![]() ,
знаяграфик
,
знаяграфик![]() и описывать их свойства.
и описывать их свойства.
42
Поисковая
Проблемные задания, фронтальный опрос, упражнения
Групповая, Построение алгоритма действия, решение упражнений.
Могут график ![]() вытянуть и сжать от оси
вытянуть и сжать от оси
![]() , в зависимости
от значения
, в зависимости
от значения ![]() .
Умеют работать с учебником, отбирать и структурировать материал.
(Р)
.
Умеют работать с учебником, отбирать и структурировать материал.
(Р)
Могут график ![]() вытянуть и сжать от оси
вытянуть и сжать от оси
![]() , в зависимости
от значения
, в зависимости
от значения ![]() .
Умеют передавать, информацию сжато, полно, выборочно. (И)
.
Умеют передавать, информацию сжато, полно, выборочно. (И)
Создание компьютерной презентации о преобразованиях графиков функций
§10; §17 № 7-8(а,б), 14 (а)
43
Комбинированная
Практикум, фронтальный опрос, упражнения
Индивидуальная, работа с опорными конспектами, работа с раздаточными материалами
Могут график ![]() вытянуть и сжать от оси
вытянуть и сжать от оси
![]() , в зависимости
от значения
, в зависимости
от значения ![]() .
Используют для решения познавательных задач справочную
литературу. (П)
.
Используют для решения познавательных задач справочную
литературу. (П)
Могут график ![]() вытянуть и сжать от оси
вытянуть и сжать от оси
![]() , в зависимости
от значения
, в зависимости
от значения ![]() .
Могут привести примеры, подобрать аргументы, сформулировать
выводы. (ТВ)
.
Могут привести примеры, подобрать аргументы, сформулировать
выводы. (ТВ)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§10; §18 № 2-4(а,б), 8(а)
Тема: График гармонических колебаний (1ч).
Цели урока:формирование понятия графика гармонического
колебания; овладение алгоритмом построения графика
функции ![]() .
.
44
Проблемное изложение
Практикум, фронтальный опрос
демонстрация слайд - лекции
Фронтальная.
Работа с конспектом, работа с книгой и наглядными пособиями.
Знают формулу гармонических колебаний и имеют представление о графике гармонических колебаний. Могут собрать материал для сообщения по заданной теме. (Р)
Могут описать колебательный процесс графически. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Приобретают умения включение своих результатов в результаты работы группы
§19, №2(б), 3(б), 4
Тема: Функции ![]() ,
, ![]() (2ч).
(2ч).
Цели урока:формирование представления учащихся о
тригонометрических функциях ![]() ,
, ![]() , их свойствах; формирование
умения учащихся совершать преобразования графиков
функций
, их свойствах; формирование
умения учащихся совершать преобразования графиков
функций![]() ,
,
![]() , зная
их свойства; овладение умением учащихся свободно строить
графики функций повышенной сложности и описывать их свойства.
, зная
их свойства; овладение умением учащихся свободно строить
графики функций повышенной сложности и описывать их свойства.
45
Поисковая
Практикум, фронтальный опрос
демонстрация слайд - лекции
Групповая, работа с опорными конспектами, работа с раздаточными материалами.
Имеют представление о тригонометрических функциях ![]() ,
, ![]() , их свойствах и
могут строить графики. Используют для решения познавательных
задач справочную литературу. Умеют вступать в речевое общение,
участвовать в диалоге. (Р)
, их свойствах и
могут строить графики. Используют для решения познавательных
задач справочную литературу. Умеют вступать в речевое общение,
участвовать в диалоге. (Р)
Могут совершать преобразование графика функции![]() ,
, ![]() , зная ее свойства;
могут решать графически уравнения. Умеют определять понятия,
приводить доказательства. (И)
, зная ее свойства;
могут решать графически уравнения. Умеют определять понятия,
приводить доказательства. (И)
Приобретают умения самостоятельной и коллективной деятельности.
§11; §20 № 1-5(а), 6-7(а,б)
46
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная. Построение алгоритма действия, решение упражнений.
Знают тригонометрическую функции![]() ,
, ![]() , ее свойства и могут
строить график. Умеют работать с учебником, отбирать и
структурировать материал. Умеют проводить самооценку собственных
действий. (П)
, ее свойства и могут
строить график. Умеют работать с учебником, отбирать и
структурировать материал. Умеют проводить самооценку собственных
действий. (П)
Могут совершать преобразование графика функции![]() ,
, ![]() , зная ее свойства;
могут решать графически уравнения. Умеют передавать, информацию
сжато, полно, выборочно. (ТВ)
, зная ее свойства;
могут решать графически уравнения. Умеют передавать, информацию
сжато, полно, выборочно. (ТВ)
Поиск нужной информации в различных источниках
§11; §20 № 16-20(а)
Тема: Обратные тригонометрические функции (3ч).
Цели урока:формирование представления учащихся об обратных тригонометрических функциях, их свойства; формирование умения учащихся преобразовывать выражения, содержащие обратные тригонометрические функции; овладение умением учащихся свободно строить графики обратных тригонометрических функций повышенной сложности и описывать их свойства.
47
Проблемное изложение
Практикум, фронтальный опрос
демонстрация слайд - лекции
Фронтальная, групповая. Работа с конспектом, с книгой.
Имеют представление об обратных тригонометрических функциях, их свойства, графики. Умеют извлекать необходимую информацию из учебно-научных текстов. Умеют, развернуто обосновывать суждения. (Р)
Могут преобразовывать выражения, содержащие обратные тригонометрические функции. Могут привести примеры, подобрать аргументы, сформулировать выводы. (И)
Приобретают умения самостоятельной и коллективной деятельности.
§12; §21 № 13-15 (а,б), 17(а), §22 № 1-2(а,б)
48
Поисковая
проблемные задания, индивидуальный опрос
Групповая, индивидуальная. Построение алгоритма действия, решение упражнений.
Знают обратные тригонометрические функции, их свойства, графики. Могут собрать материал для сообщения по заданной теме. Умеют вступать в речевое общение, участвовать в диалоге. (П)
Могут преобразовывать выражения, содержащие обратные тригонометрические функции. Умеют составлять текст научного стиля. (И)
Самостоятельная работа с источниками информации, анализ обобщения и систематизации полученной информации.
§13; §21 № 1-2(а,б), 16, 19(а,б), §22 № 8-10(а,б)
49
Комбинированная
Практикум, фронтальный опрос, упражнения
Индивидуальная. Работа с опорными конспектами, работа с раздаточными материалами
Знают обратные тригонометрические функции, их свойства, графики. Используют для решения познавательных задач справочную литературу. (П)
Могут преобразовывать выражения, содержащие обратные тригонометрические функции. Могут составить набор карточек с заданиями. (ТВ)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§14; §21 № 31-33 (а,б), §22 № 17-20 (а,б)
Тригонометрические уравнения (10 ч).
Основные цели: создать условия учащимся для:
-
Расширения и обобщения сведения о видах тригонометрических уравнений.
-
Формирования умения решения разными методами тригонометрических уравнений.
-
Формирования представления об однородном тригонометрическом уравнении.
Тема: Простейшие тригонометрические уравнения и неравенства (4ч).
Цели урока:формирование представления учащихся об
арккосинусе, арксинусе; формирование умения учащихся
решать простейшие уравнения![]() ,
, ![]() .,
., ![]() и
и ![]() ; овладение
умением учащихся строить график арккосинуса, арксинуса и
решать неравенства
; овладение
умением учащихся строить график арккосинуса, арксинуса и
решать неравенства ![]() ,
, ![]() ,
, ![]() и
и ![]() ; овладение
умением решать простейшие тригонометрические уравнения
введением новой переменной и разложением на множители;
формирование умения учащихся решать по алгоритму
однородные уравнения.
; овладение
умением решать простейшие тригонометрические уравнения
введением новой переменной и разложением на множители;
формирование умения учащихся решать по алгоритму
однородные уравнения.
50
Поисковая
Практикум, фронтальный опрос демонстрация слайд - лекции
Групповая, работа с опорными конспектами, работа с раздаточными материалами
Имеют представление об арккосинусе, арксинусе и могут решать
простейшие уравнения ![]() ,
, ![]() . Умеют объяснить
изученные положения на самостоятельно подобранных конкретных
примерах. (Р)
. Умеют объяснить
изученные положения на самостоятельно подобранных конкретных
примерах. (Р)
Могут строить график арккосинуса, арксинуса и решать
неравенства ![]() ,
, ![]() . Умеют
работать с учебником, отбирать и структурировать материал. (И)
. Умеют
работать с учебником, отбирать и структурировать материал. (И)
Приобретают умения включение своих результатов в результаты работы группы
§22 №16-19(а,в)
51
Поисковая
Практикум, фронтальный опрос, упражнения
Групповая, индивидуальная, работа раздаточными материалами.
Знают определение арктангенса.арккотангенса и могут решать
простейшие уравнения![]() и
и ![]() . Умеют определять понятия,
приводить доказательства. (П)
. Умеют определять понятия,
приводить доказательства. (П)
Могут строить график арктангенса, арккотангенса и решать
неравенства ![]() и
и
![]() . Умеют
передавать, информацию сжато, полно, выборочно. (И)
. Умеют
передавать, информацию сжато, полно, выборочно. (И)
Самостоятельно искать, необходимую для решения учебных задач информацию
§15 №26-28
52
Проблемное изложение
Проблемные задачи
Фронтальная, работа с демонстрационным материалом
Могут решать простейшие тригонометрические уравнения по формулам. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Могут решать простейшие тригонометрические уравнения введением новой переменной и разложением на множители; решают по алгоритму однородные уравнения (ТВ)
Создание презентации о способах решения тригоно метрических уравнений.
§22 №21-22 (а,в,г)
53
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная. Построение алгоритма действия, решение упражнений, ответы на вопросы.
Могут решать простейшие тригонометрические уравнения по формулам. Используют для решения познавательных задач справочную литературу. Умеют, развернуто обосновывать суждения. (П)
Могут решать простейшие тригонометрические уравнения введением новой переменной и разложением на множители; решают по алгоритму однородные уравнения (ТВ)
Использование различной литературы для создания презентации своего проекта обобщения материала
§22, №42(в,г),43(в,г)
Тема: Методы решения тригонометрических уравнений (4ч).
Цели урока: формирование представлений учащимися о простейших тригонометрических уравнениях; овладение навыками и умениями решать простейшие тригонометрические уравнения введением новой переменной и разложением на множители; формирование умения решать по алгоритму однородные уравнения; формирование умения самостоятельно выбрать метод решения тригонометрического уравнения.
54
Поисковая
Практикум, фронтальный опрос
демонстрация слайд - лекции
Групповая, работа с конспектами, работа с раздаточными материалами
Знают, как решать простейшие тригонометрические уравнения по формулам. Умеют извлекать необходимую информацию из учебно-научных текстов. Могут найти и устранить возникших трудностей. (Р)
Могут решать простейшие тригонометрические уравнения введением новой переменной и разложением на множители; решают по алгоритму однородные уравнения (И)
Приобретают умения включение своих результатов в результаты работы группы
§15; §22 № 23-26 (а,б), 27(а,в)
55
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Фронтальная, групповая. Работа с конспектом, работа с книгой и наглядными пособиями.
Могут решать тригонометрические уравнения методом замены переменной, методом разложения на множители. Умеют находить и использовать информацию. (П)
Могут самостоятельно выбрать метод решения тригонометрического уравнения. Умеют составлять текст научного стиля. Могут излагать информацию, обосновывая свой собственный подход. (И)
Создание компьютерной презентации о способах решения
тригонометрических уравнений.
§15; §23 № 1-10(а)
56
Поисковая
проблемные задания, фронтальный опрос, упражнения
Групповая, индивидуальная. Построение алгоритма действия, решение упражнений.
Могут решать однородные тригонометрические уравнения первой степени. Могут привести примеры, подобрать аргументы, сформулировать выводы. Могут излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. (П)
Могут самостоятельно выбрать метод решения тригонометрического уравнения. Могут собрать материал для сообщения по заданной теме. Умеют участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение. (ТВ)
Использование различной литературы для создания презентации своего проекта обобщения материала
§15; §23 № 11-17(а)
57
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная. Работа с раздаточными материалами.
Могут решать однородные тригонометрические уравнения второй степени. Умеют составлять текст научного стиля. Умеют, развернуто обосновывать суждения. (П)
Могут самостоятельно выбрать метод решения тригонометрического уравнения. Могут составить набор карточек с заданиями. (ТВ)
Развитие умения производить рассуждения, проводить обобщение
§15; §23 № 18-23(а), 24(а)
Контрольная работа № 6 (2 ч)
Цель урока проверить знания и умение учащихся по теме тригонометрические уравнения.
58-59
Урок контроля, оценки и коррекции знаний
Самостоятельное планирование и проведение исследования решения
Индивидуальное решение контрольных заданий.
Учащихся демонстрируют умение расширять и обобщать сведения о видах тригонометрических уравнений; умение решения разными методами тригонометрических уравнений (П)
Могут самостоятельно выбрать метод решения тригонометрического уравнения. Владеют навыками самоанализа и самоконтроля. (ТВ)
Владеют навыками самоанализа и самоконтроля
4, 5
проблемные дифференцированные задания
Преобразование тригонометрических выражений (21
ч).
Основные цели: создать условия учащимся для:
-
Формирования умения вывода формул приведения, двойного угла, понижения степени, синуса, косинуса, тангенса и котангенса суммы и разности углов, перевода произведения в сумму и наоборот.
Расширения и обобщения сведения о преобразовании тригонометрических выражениях, применяя различные формулы.
Тема: Синуса и косинуса суммы и разности аргумента (3ч).
Цели урока: формирование представлений учащимися о формуле синуса, косинуса суммы и разности двух углов; могут преобразовывать простейшие выражения, используя основные тождества, формулы приведения; овладение навыками и умениями определять действительную и мнимую часть, модуль и аргумент комплексного числа; формирование умения решать простейшие тригонометрические уравнения и простейшие тригонометрические неравенства, используя преобразования выражений.
60
Объяснительно-иллюстративная
Беседа, демонстрация
таблиц
Фронтальная, индивидуальная, работа с демонстрационным материалом.
Имеют представление о формуле синуса, косинуса суммы и разности двух углов; могут преобразовывать простейшие выражения, используя основные тождества, формулы приведения. Умеют определять понятия, приводить доказательства (Р)
Могут решать простейшие тригонометрические уравнения и простейшие тригонометрические неравенства, используя преобразования выражений. Умеют определять понятия, приводить доказательства. (И)
Перевод понятий из одной знаковой системы в другую.
§16; §24 № 3-6(а,б), 15-18(а)
61
Комбинированная
Практикум, фронтальный опрос, упражнения
Индивидуальная, работа с опорными конспектами, работа с раздаточными материалами.
Знают формулу синуса, косинуса суммы и разности двух углов; могут преобразовывать простые выражения, используя основные тождества, формулы приведения. Используют для решения познавательных задач справочную литературу. (П)
Могут решать простейшие тригонометрические уравнения и простейшие тригонометрические неравенства, используя преобразования выражений Умеют работать с учебником, отбирать и структурировать материал. (И)
Уметь находить и использовать информацию
§16; §24 № 12(а), 19 (а,б), 20-23(а)
62
Комбинированная
Практикум, фронтальный опрос, упражнения
Индивидуальная. Работа с раздаточными материалами.
Знают формулу синуса, косинуса суммы и разности двух углов; могут преобразовывать простые выражения, используя основные тождества, формулы приведения. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Могут решать простейшие тригонометрические уравнения и простейшие тригонометрические неравенства, используя преобразования выражений. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (ТВ)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§16; §24 № 27-28 (а,б), 34
Тема: Тангенса суммы и разности аргумента (2ч).
Цели урока: формирование представлений учащимися о формуле тангенса и котангенса суммы и разности двух углов; овладение навыками и умениями преобразовывать простые тригонометрические выражения; формирование умения решать простейшие тригонометрические уравнения и простейшие тригонометрические неравенства, используя преобразования выражений.
63
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Фронтальная, индивидуальная. Построение алгоритма действия, решение упражнений.
Имеют представление о формуле тангенса и котангенса суммы и разности двух углов; могут преобразовывать простые тригонометрические выражения. Умеют извлекать необходимую информацию из учебно-научных текстов. (Р)
Могут решать простейшие тригонометрические уравнения и простейшие тригонометрические неравенства, используя преобразования выражений. Умеют находить и использовать информацию. (И)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§17; §25 № 5(а,б), 7 (а), 10(а), 11(а)
64
Комбинированная
Практикум, фронтальный опрос
Индивидуальная. Решение упражнений, составление опорного конспекта.
Знают формулу тангенса и котангенса суммы и разности двух углов; могут преобразовывать простые тригонометрические выражения. Умеют объяснить изученные положения на самостоятельно подобранных примерах.
Могут решать простейшие тригонометрические уравнения и простейшие тригонометрические неравенства, используя преобразования выражений. (ТВ)
Поиск нужной информации в различных источниках
§17; §25 № 14(а), 15(б), 17-18(а), 22 (а,б)
Тема: Формулы приведения (2ч).
Цели урока: формирование представлений учащимися о формулах приведения; овладение навыками и умениями упрощать выражения, используя основные тригонометрические тождества и формулы приведения; формирование упрощать выражения, используя основные тригонометрические тождества и формулы приведения; доказывать тождества
65
Объяснительно-иллюстративная
Лекция, демонстрация
плакатов и таблиц
Индивидуальная.
Решение качественных задач.
Знают вывод формул приведения. Могут упрощать выражения, используя основные тригонометрические тождества и формулы приведения (Р)
Могут упрощать выражения, используя основные тригонометрические тождества и формулы приведения; доказывать тождества (И)
Поиск нужной информации по заданной теме в источниках различного типа.
§26, №7, 9, 14, 16
66
Комбинированная
Практикум, фронтальный опрос
Фронтальная. Построение алгоритма действия, решение упражнений.
Знают вывод формул приведения. Могут упрощать выражения, используя основные тригонометрические тождества и формулы приведения (П)
Могут упрощать выражения, используя основные тригонометрические тождества и формулы приведения; доказывать тождества (ТВ)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§26, №22(б), 23-25
Тема: Формулы двойного угла. Формулы понижения степени. Формулы половинного угла. (3ч).
Цели урока: формирование представлений учащимися о формулах двойного угла и понижения степени синуса, косинуса и тангенса; овладение навыками и умениями применять формулы для упрощения выражений; формирование умения вывести и применять при упрощении выражений формулы половинногоугла; выражать функции через тангенс половинного аргумента.
67
Объяснительно-иллюстративная
беседа, демонстрация
таблиц
Фронтальная. Построение алгоритма действия, решение упражнений.
Имеют представление о формулах двойного угла и понижения степени синуса, косинуса и тангенса; могут применять формулы для упрощения выражений. Умеют работать с учебником, отбирать и структурировать материал. (Р)
Могут вывести и применять при упрощении выражений формулы половинногоугла; выражать функции через тангенс половинного аргументаУмеют передавать, информацию сжато, полно, выборочно. (И)
Использование справочной литературы, а также материалов ЕГЭ
§18; §27 № 1-7(а,б)
68
Комбинированная
Практикум, фронтальный опрос
Индивидуальная.
Решение качественных задач.
Знают формулы двойного угла и понижения степени синуса, косинуса и тангенса; могут применять формулы для упрощения выражений. Умеют находить и использовать информацию. (П)
Могут вывести и применять при упрощении выражений формулы половинногоугла; выражать.функции через тангенс половинного аргумента. Могут найти и устранить причины возникших трудностей. (И)
Составление обобщающих информационных таблиц (конспектов)
§18; §27 № 12-16 (а,б)
69
Поисковая
Организация совместной учебной деятельности
Групповая. Построение алгоритма действия, решение упражнений
Знают формулы двойного, половинного угла, понижения степени синуса, косинуса и тангенса; могут применять формулы для упрощения выражений. Умеют извлекать необходимую информацию из учебно-научных текстов. (П)
Могут вывести и применять при упрощении выражений формулы половинногоугла; выражать функции через тангенс половинного аргумента. Могут собрать материал для сообщения по заданной теме (ТВ)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§18; §27 №27, 48-52 (а)
Тема: Преобразование сумм тригонометрических функций в произведение (3 ч).
Цели урока: формирование представлений учащимися о преобразовании суммы тригонометрических функций в произведение; преобразовании простых тригонометрических выражений; формирование умения вывести и применять при упрощении выражений формулы преобразований сумм в произведения..
70
Объяснительно-иллюстративная
беседа, демонстрация
таблиц
Групповая. Построение алгоритма действия, решение упражнений.
Имеют представление как преобразовывать суммы тригонометрических функций в произведение; преобразования простых тригонометрических выражений. Используют для решения познавательных задач справочную литературу. (Р)
Могут вывести и применять при упрощении выражений формулы преобразований сумм в произведения. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (И)
Использование справочной литературы, а также материалов ЕГЭ
§19; §28 № 1-6(а,б)
71
Комбинированная
Практикум. Организация совместной учебной деятельности
Индивидуальная. Построение алгоритма действия, решение упражнений.
Умеют преобразовывать суммы тригонометрических функций в произведение; преобразования простых тригонометрических выражений. Умеют определять понятия, приводить доказательства. (П)
Могут вывести и применять при упрощении выражений формулы преобразований сумм в произведения. Умеют работать с учебником, отбирать и структурировать материал. (И)
Поиск нужной информации в различных источниках
§19; §28 № 8-9(а), 14(а,б), 15(а), 16(а)
72
Поисковая
Организация совместной учебной деятельности
Групповая Составление опорного конспекта, решение задач.
Умеют преобразовывать суммы тригонометрических функций в произведение; преобразования простых тригонометрических выражений. Умеют определять понятия, приводить доказательства.(П)
Могут вывести и применять при упрощении выражений формулы преобразований сумм в произведения. Умеют передавать, информацию сжато, полно, выборочно. (ТВ)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§19; §28 № 26-33(а)
Тема: Преобразование произведения тригонометрических функций в сумму (2 ч).
Цели урока: формирование представлений учащимися о преобразовании произведения тригонометрических функций в сумму; преобразовании простейших тригонометрических выражений; овладение навыками и умениями упрощении выражений формулы преобразований сумм в произведения и наоборот: преобразование произведений в суммы; формирование умения вывести и применять при упрощении выражений формулы преобразований сумм в произведения и наоборот: преобразование произведений в суммы.
73
Объяснительно-иллюстративная
Беседа, демонстрация таблиц
Фронтальная, групповая. Работа с конспектом, работа с книгой и наглядными пособиями.
Имеют представление, как преобразовывать произведения тригонометрических функций в сумму; преобразования простейших тригонометрических выражений. Умеют извлекать необходимую информацию из учебно-научных текстов. (Р)
Могут вывести и применять при упрощении выражений формулы преобразований сумм в произведения и наоборот: преобразование произведений в суммы. Умеют находить и использовать информацию. (И)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§20, §29 №4-9(А0
74
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная, работа с опорными конспектами, работа с раздаточными материалами.
Знают, как преобразовывать произведения тригонометрических функций в сумму; преобразования простейших тригонометрических выражений. Могут привести примеры, подобрать аргументы, сформулировать выводы. (П)
Могут вывести и применять при упрощении выражений формулы преобразований сумм в произведения и наоборот: преобразование произведений в суммы. Могут собрать материал для сообщения по заданной теме. (ТВ)
Использование различной литературы для создания презентации своего проекта обобщения материала
§20; §29 № 12-15(а)
Тема: Преобразование выражений
![]() к виду
к виду
![]() (1 ч).
(1 ч).
Цели урока: формирование представлений учащимися о формуле перехода от суммы двух функций с различными коэффициентами в одну из тригонометрических функций; формирование умения использовать формулу перехода от суммы двух функций с различными коэффициентами в одну из тригонометрических функций
75
Объяснительно-иллюстративная
Беседа, работа с книгой
Фронтальная, Конспектируют лекцию, продумывают примеры, отвечают на вопросы
Знают формулу перехода от суммы двух функций с различными коэффициентами в одну из тригонометрических функций. Умеют составлять текст научного стиля. (Р)
Умеют использовать формулу перехода от суммы двух функций с различными коэффициентами в одну из тригонометрических функций (П)
Уметь находить и использовать информацию
§20; §29 № 20-23(а)
Тема: Методы решения тригонометрических уравнений (3ч).
Цели урока: формирование представлений учащимися о методе вспомогательного аргумента при решении тригонометрических уравнений; овладение навыками и умениями применять метод вспомогательного аргумента при решении тригонометрических уравнений; формирование умения применять частные случаи метода введения новой переменной при решении тригонометрических уравнений
76
Проблемное изложение
Практикум, фронтальный опрос
демонстрация слайд - лекции
Фронтальная, групповая работа с конспектом, работа с книгой.
Имеют представление о методе вспомогательного аргумента при решении тригонометрических уравнений. Могут составить набор карточек с заданиями. (Р)
Умеют применять метод вспомогательного аргумента при решении тригонометрических уравнений. Могут найти и устранить причины возникших трудностей. (И)
Приобретают умения самостоятельной и коллективной деятельности.
§31, №4, 6, 7(б)
77
Поисковая
Проблемные задания, фронтальный опрос, упражнения
Групповая, индивидуальная, работа с опорными конспектами.
Знаю частный случай метода введения новой переменной при решении тригонометрических уравнений. Умеют, развернуто обосновывать суждения. (П)
Умеют применять частный случай метода введения новой переменной при решении тригонометрических уравнений (И)
Поиск нужной информации в различных источниках
§31, №12, 13, 14
78
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная, работа с раздаточными материалами.
Знаю частный случай метода введения новой переменной при решении тригонометрических уравнений. Умеют составлять текст научного стиля. (П)
Умеют применять частный случай метода введения новой переменной при решении тригонометрических уравнений (ТВ)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§31, №24, 25
Контрольная работа №8 (2 ч)
Цель урока проверить знания и умение учащихся по теме тригонометрические выражения.
79-80
Урок контроля, оценки и коррекции знаний
Самостоятельное планирование и проведение исследования решения
Индивидуальное решение контрольных заданий.
Учащихся демонстрируют умение расширять и обобщать сведения о преобразовании тригонометрических выражениях, применяя различные формулы. (П)
Могут самостоятельно выбрать метод решения тригонометрического
уравнения. Владеют навыками самоанализа и самоконтроля.
(ТВ)
Владеют навыками самоанализа и самоконтроля
4, 5
проблемные дифференцированные задания.
Комплексные числа (9ч).
Основные цели: создать условия учащимся для:
-
Формирования представления о комплексных числах и операциях над ними; ввести две формы записи комплексного числа.
-
Овладением навыками и умениями выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами.
Тема: Комплексные числа и арифметические операции над ними (2ч).
Цели урока: формирование представлений учащимися о комплексных числах; овладение навыками и умениями определять действительную и мнимую часть, модуль и аргумент комплексного числа; формирование умения выполнять арифметические действия над комплексными числами в разных формах записи.
81
Проблемное изложение
лекция, демонстрация
Фронтальная, индивидуальная, работа с опорными конспектами, работа с раздаточными материалами.
Имеют представление, что такое комплексные числа; могут определить действительную и мнимую часть, модуль и аргумент комплексного числа. Могут выполнять арифметические действия над комплексными числами в разных формах записи. Умеют определять понятия, приводить доказательства. (Р)
Могут определить действительную и мнимую часть, модуль и аргумент комплексного числа. Могут выполнять арифметические действия над комплексными числами в разных формах записи. Умеют работать с учебником, отбирать и структурировать материал. (И)
Поиск нужной информации в различных источниках
§32, №15, 17
82
Комбинированная
Практикум, фронтальный опрос, упражнения
Групповая, индивидуальная, работа со
сборником задач, ответы на вопросы.
Знают комплексные числа; могут определить действительную и мнимую часть, модуль и аргумент комплексного числа. Могут выполнять арифметические действия над комплексными числами в разных формах записи. Используют для решения познавательных задач справочную литературу (П)
Могут определить действительную и мнимую часть, модуль и аргумент комплексного числа. Могут выполнять арифметические действия над комплексными числами в разных формах записи. Могут найти и устранить причины возникших трудностей. (ТВ)
Использование различной литературы для создания презентации своего проекта обобщения материала
§32, №21, 22, 27(б)
Тема: Комплексные числа и координатная плоскость (1ч).
Цели урока: формирование представлений учащимися о геометрической интерпретации комплексных чисел, действительной и мнимой части комплексного числа; овладение навыками и умениями определять геометрическую интерпретацию комплексных чисел, действительной и мнимой части комплексного числа; формирование умения нахождения модуля и аргумента комплексного числа .
83
Комбинированная
Практикум, фронтальный опрос, упражнения
Групповая, индивидуальная. Решение упражнений, составление опорного конспекта.
Знают геометрическую интерпретацию комплексных чисел, действительной и мнимой части комплексного числа; могут найти модуль и аргумент комплексного числа. Умеют определять понятия, приводить доказательства. (Р)
Могут определять геометрическую интерпретацию комплексных чисел, действительной и мнимой части комплексного числа; могут найти модуль и аргумент комплексного числа (П)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§33, №3, 13
Тема: Тригонометрическая форма записи комплексного числа (2ч).
Цели урока: формирование представлений учащимися о действительной и мнимой части комплексного числа, о модуле и аргументе комплексного числа; овладение навыками и умениями определять действительную и мнимую часть, модуль и аргумент комплексного числа; формирование умения записывать комплексные числа в тригонометрической форме записи.
84
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Групповая, индивидуальная, работа с демонстрационным материалом,
Имеют представление, как определить действительную и мнимую часть, модуль и аргумент комплексного числа; могут записывать комплексные числа в тригонометрической форме записи (Р).
Могут определить действительную и мнимую часть, модуль и аргумент комплексного числа; могут записывать комплексные числа в тригонометрической форме записи (И)
Поиск нужной информации в различных источниках
§34, №12(в,г), 13(в,г)
85
Комбинированная
Практикум, индивидуальный опрос
Групповая, индивидуальная. Решение упражнений, составление опорного конспекта, ответы на вопросы.
Знают, как определить действительную и мнимую часть, модуль и аргумент комплексного числа; могут записывать комплексные числа в тригонометрической форме записи. Умеют обосновывать суждения, давать определения, приводить доказательства, примеры (Р)
Могут определить действительную и мнимую часть, модуль и аргумент комплексного числа; могут записывать комплексные числа в тригонометрической форме записи. Используют компьютерные технологии для создания базы данных. (ТВ)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§34, №21, 22, 23
Тема: Комплексные числа и квадратные уравнения (1ч).
Цели урока: формирование представлений учащимися о корне квадратного уравнения с отрицательным дискриминантом; формирование уменияизвлекать квадратные корни из комплексного числа.
86
Комбинированная
Практикум, фронтальный опрос, упражнения
Групповая, индивидуальная. Решение упражнений.
Знают, как найти корни квадратного уравнения с отрицательным дискриминантом. Умеют извлекать необходимую информацию из учебно-научных текстов. (Р)
Могут извлекать квадратные корни из комплексного числа. Могут привести примеры, подобрать аргументы, сформулировать выводы. (П)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§35, №7(в,г), 8(в,г)
Тема: Возведение комплексного числа в степень. Извлечение кубического корня из комплексного числа (2ч).
Цели урока: формирование представлений учащимися о комплексно сопряженных числах, о возведение в натуральную степень (формула Муавра), об основной теореме алгебры; овладение навыками и умениями выполнять арифметические действия над комплексными числами в разных формах записи.
87
Объяснительно-иллюстративная
Беседа, работа с книгой
Фронтальная, индивидуальная, работа со сборником задач,
Могут выполнять арифметические действия над комплексными числами в разных формах записи. Знают комплексно сопряженные числа.
Знают комплексно сопряженные числа; возведение в натуральную степень (формула Муавра), основную теорему алгебры.. (И)
Поиск нужной информации в различных источниках
§36, №7, 8, 9, 16
88
Комбинированная
Практикум, индивидуальный опрос
Групповая, индивидуальная, работа раздаточными материалами
Могут выполнять арифметические действия над комплексными числами в разных формах записи. Знают комплексно сопряженные числа. Могут составить набор карточек с заданиями. (П)
Знают комплексно сопряженные числа; возведение в натуральную степень (формула Муавра), основную теорему алгебры. Умеют, развернуто обосновывать
Сбор материала для сообщения по заданной теме
§36, №12, 20(в)
Контрольная работа № 9
Цель урока проверить знания и умение учащихся по теме комплексные числа
89
Урок контроля, оценки и коррекции знаний
Самостоятельное планирование и проведение исследования решения
Индивидуальное решение контрольных заданий.
Учащихся демонстрируют умение расширять и обобщать сведения о комплексных числах и операциях над ними. а также ввести две формы записи комплексного числа. (П)
Могут свободно вводить и использовать две формы записи комплексного числа. Владеют навыками самоанализа и самоконтроля. (ТВ)
Владеют навыками самоанализа и самоконтроля
4, 5
проблемные дифференцированные задания.
Производная (28 ч).
Основные цели: создать условия учащимся для:
-
Формулирования представлений о правилах вычисления производных, о понятии предела числовой последовательности и предела функции
-
Овладения умением вывода формул производных различных функций; исследования функции, с помощью производной; составление уравнения касательной к графику функции.
Тема: Числовые последовательности (2ч).
Цели урока: формирование представлений учащимися об определение числовой последовательности и способах ее задания; овладение навыками и умениями задавать числовые последовательности различными способами; формирование умения применять свойства числовых последовательностей
90
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Групповая, индивидуальная, работа со
сборником задач, ответы на вопросы.
Знают определение числовой последовательности и способы ее задания. Используют для решения познавательных задач справочную литературу. (Р)
Умеют задавать числовые последовательности различными способами. Умеют работать с учебником, отбирать и структурировать материал (И)
Работа со справочной литературой
§37, № 5(а,б), 10(а,б), 18(а), 27(а,б)
91
Комбинированная
Практикум, фронтальный опрос, упражнения
Групповая, индивидуальная. Работа с раздаточными материалами
Знают и могут привести примеры на свойства числовой последовательности. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Умеют применять свойства числовых последовательностей. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (ТВ)
Использование справочной литературы, а также материалов ЕГЭ
§28; §38, № 14-19(а,б)
Тема: Предел числовой последовательности (2ч).
Цели урока: формирование представлений учащимися об определение предела числовой последовательности и свойства сходящихся последовательностей; овладение навыками и умениями находить предел числовой последовательности, используя свойства сходящихся последовательностей; формирование умения вычислять пределы последовательностей и находить сумму бесконечной геометрической прогрессии.
92
Проблемное изложение
Проблемные задачи, индивидуальный опрос
Групповая, индивидуальная. Построение алгоритма действия.
Знают определение предела числовой последовательности; свойства сходящихся последовательностей. Умеют определять понятия, приводить доказательства. Могут собрать материал для сообщения по заданной теме (Р)
Умеют находить предел числовой последовательности, используя свойства сходящихся последовательностей. Умеют составлять текст научного стиля (И)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§29; §38, № 23-27(а)
93
Комбинированная
Практикум, фронтальный опрос, упражнения
Групповая, индивидуальная. Работа с опорными конспектами,
Знают способы вычисления пределов последовательностей. Знают, как найти сумму бесконечной геометрической прогрессии. Могут составить набор карточек с заданиями. (П)
Умеют вычислять пределы последовательностей и находить сумму бесконечной геометрической прогрессии. Умеют, развернуто обосновывать суждения. (ТВ)
Сбор материала для сообщения по заданной теме
§28; §38, № 30(а), 33(а,б), 36(а,б)
Тема: Предел функции (2ч).
Цели урока: формирование представлений учащимися о непрерывности функции, о понятии пределе функции на бесконечности и в точке;овладение навыками и умениями посчитать приращение аргумента и функции; формирование умения определить существование предела монотонной ограниченной последовательности.
94
Объяснительно-иллюстративная
Практикум, фронтальный опрос
демонстрация слайд - лекции
Фронтальная, индивидуальная, работа с раздаточными материалами
Имеют представление о понятии пределе функции на бесконечности и в точке; могут посчитать приращение аргумента и функции; могут вычислить простейшие пределы. Умеют определять понятия, приводить доказательства. (Р)
Могут определить существование предела монотонной ограниченной последовательности; знают понятие о непрерывности функции. Могут собрать материал для сообщения по заданной теме. (И)
Приобретают умения самостоятельной и коллективной деятельности.
§21; §39, № 11-14(а,б)
95
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Групповая, работа со
сборником задач, ответы на вопросы.
Знают понятие о пределе функции на бесконечности и в точке; могут посчитать приращение аргумента и функции; могут вычислить простейшие пределы. Умеют, развернуто обосновывать суждения.
Могут определить существование предела монотонной ограниченной последовательности; знают понятие о непрерывности функции. Умеют, развернуто обосновывать суждения.
Создание компьютерной презентации о пределе функции.
§21; §39, № 14-17(а,б), 23-25(а,б)
Тема: Определение производной (2ч).
Цели урока: формирование представлений учащимися о понятии производной функции, физическом и геометрическом смысле производной; овладение навыками и умениями использовать алгоритм нахождения производной простейших функций; формирование умения вывести формулы нахождения производной используя определение производной.
96
Объяснительно-иллюстративная
беседа, демонстрация
Групповая, индивидуальная, работа с опорными конспектами,
Имеют представление о понятии производной функции, физический и геометрический смысл производной. Умеют извлекать необходимую информацию из учебно-научных текстов (Р)
Могут использовать алгоритм нахождения производной простейших функций. Могут привести примеры, подобрать аргументы, сформулировать выводы. (И)
Развитие умения производить аргументированные рассуждения, проводить обобщение
§22; §40, № 4(а,б), 14(а,б), 39, 45
97
Проблемное изложение
Проблемные задачи, индивидуальный опрос
Групповая. Построение алгоритма действия, решение упражнений.
Знают понятие о производной функции, физический и геометрический смысл производной. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах (П)
Могут использовать алгоритм нахождения производной простейших функций. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (ТВ)
Использование справочной литературы, а также материалов ЕГЭ
§22; §40, № 15-16(а,б)
Тема: Вычисление производной (3ч).
Цели урока: формирование представлений учащимися о нахождении производные суммы, разности, произведения, частного; овладение навыками и умениями находить производные основных элементарных функций; формирование умения вывести формулы нахождения производной.
98
Проблемное изложение
Проблемные задачи, индивидуальный опрос
Фронтальная. Конспектируют лекцию, продумывают примеры,
Знают, как находить производные суммы, разности, произведения, частного; производные основных элементарных функций. Используют для решения познавательных задач справочную литературу. (Р)
Могут вывести формулы нахождения производной; вычислять скорость изменения функции в точке. Умеют работать с учебником, отбирать и структурировать материал (И)
Поиск нужной информации в различных источниках
§23; §41, № 5-12(а,б)
99
Комбинированная
Практикум, фронтальный опрос, упражнения
Индивидуальная, работа с опорными конспектами, работа с раздаточными материалами
Могут находить производные суммы, разности, произведения, частного; производные основных элементарных функций. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Могут вывести формулы нахождения производной; вычислять скорость изменения функции в точке. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (И)
Составление обобщающих информационных таблиц (конспектов)
§23; §41, № 13-15(а,б), 18-19(а,б)
100
Поисковая
Организация совместной учебной деятельности
Групповая, работа с опорными конспектами, работа с раздаточными материалами.
Могут находить производные суммы, разности, произведения, частного; производные основных элементарных функций. Умеют извлекать необходимую информацию из учебно-научных текстов. (П)
Могут вывести формулы нахождения производной; вычислять скорость изменения функции в точке. Могут привести примеры, подобрать аргументы, сформулировать выводы. (ТВ)
Умение обосновывать суждения, давать определения, приводить доказательства, примеры
§23; §41, № 21-22(а,б), 25-29(б). 42-43(а)
Тема: Дифференцирование сложной функции. Дифференцирование обратной функции (2ч).
Цели урока: формирование представлений учащимися о понятие сложной функции; овладение навыками и умениями составления сложных функций; формирование умения составлять сложные функции и их дифференцировать.
101
Проблемное изложение
Проблемные задачи, индивидуальный опрос
Фронтальная. Продумывают примеры, отвечают на вопросы
Знают понятие сложной функции; могут составлять сложные функции и их дифференцировать. Умеют передавать, информацию сжато, полно, выборочно. (Р)
Умеют выводить формулу дифференцирования сложной функции. Умеют работать с учебником, отбирать и структурировать материал. (И)
Поиск нужной информации в различных источниках
§23; §42, № 1-3(а,б), 9-10(а)
102
Комбинированная
Практикум, фронтальный опрос, упражнения
Индивидуальная, работа со
сборником задач, ответы на вопросы.
Знают понятие обратной функции; могут находить обратные функции и их дифференцировать. Умеют составлять текст научного стиля. (П)
Умеют выводить формулу дифференцирования обратной функции. Умеют, развернуто обосновывать суждения. (ТВ)
Составление обобщающих информационных таблиц (конспектов)
§23; §42, № 5-7(а,б), 11-12(а,б)
Тема: Уравнение касательной к графику функции (3ч).
Цели урока: формирование представлений учащимися о составлении уравнения касательной к графику функции по алгоритму; овладение навыками и умениями составления уравнения касательной к графику функции; формирование умения составлять уравнения касательной к графику функции при дополнительных условиях
103
Проблемное изложение
Практикум, фронтальный опрос
демонстрация слайд - лекции
Фронтальная. Конспектируют лекцию, продумывают примеры, отвечают на вопросы
Знают, как составлять уравнения касательной к графику функции по алгоритму. Умеют извлекать необходимую информацию из учебно-научных текстов. (Р)
Умеют составлять уравнения касательной к графику функции при дополнительных условиях. Могут привести примеры, подобрать аргументы, сформулировать выводы. (И)
Приобретают умения включение своих результатов в результаты работы группы
§24; §43, № 4-8(а), 12-13(а)
104
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная, работа с раздаточными материалами.
Умеют составлять уравнения касательной к графику функции по алгоритму. Умеют работать с учебником, отбирать и структурировать материал. Умеют извлекать необходимую информацию из учебно-научных текстов. (П)
Умеют составлять уравнения касательной к графику функции при дополнительных условиях. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (И)
Составление обобщающих информационных таблиц (конспектов)
§24; §43, № 16-20(а), 22(б), 23-24(а)
105
Поисковая
Организация совместной учебной деятельности
Групповая. Построение алгоритма действия, решение упражнений.
Умеют составлять уравнения касательной к графику функции по алгоритму. Умеют передавать, информацию сжато, полно, выборочно. Могут дать оценку информации, фактам, процессам, определять их актуальность. (П)
Умеют составлять уравнения касательной к графику функции при дополнительных условиях. Умеют определять понятия, приводить доказательства. Могут составить набор карточек с заданиями. (ТВ)
Самостоятельно искать, извлекать и отбирать необходимую для решения учебных задач информацию
§24; §43, № 25-26(а), 29-31(а)
Контрольная работа №10
Цель урока проверить знания и умение учащихся по теме вычисление производной и составление уравнения касательной к графику функции
106
Урок контроля, оценки и коррекции знаний
Самостоятельное планирование и проведение исследования решения
Индивидуальное решение контрольных заданий.
Учащихся демонстрируют умение вычисления производных по правилам. Ввести понятие предел числовой последовательности и функции.
Могут свободно выводить и использовать формулы производных различных функций и вычислять пределы числовых последовательностей.
Владеют навыками самоанализа и самоконтроля
4, 5
проблемные дифференцированные задания.
Тема: Применение производной для исследования функций (3 ч).
Цели урока: формирование представлений учащимися об исследовании в простейших случаях функции на монотонность; овладение навыками и умениями использовать производные при решении уравнений и неравенств, текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений; формирование умения строить графики функций, исследуя их производной.
107
Объяснительно-иллюстративная
Практикум, фронтальный опрос
демонстрация слайд - лекции
Фронтальная.
решение упражнений.
Знают, как исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики функций. (Р)
Могут использовать производные при решении уравнений и неравенств, текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений
Приобретают умения самостоятельной и коллективной деятельности.
§25; §44, № 12-16(а), 20(а,б)
108
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Групповая. Построение алгоритма действия, решение упражнений.
Умеют исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики функций. Могут составить набор карточек с заданиями (П)
Могут использовать производные при решении уравнений и неравенств, текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений (И)
Создание компьютерной презентации об исследовании функций
§25; §44, № 17-19(а), 21-25(а)
109
Проблемное изложение
Проблемные задачи. Организация совместной учебной деятельности
Групповая. Составление опорного конспекта, решение задач, работа с тестом и
Умеют исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики функций. Умеют, развернуто обосновывать суждения. (П)
Могут использовать производные при решении уравнений и неравенств, текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений (ТВ)
Умение развернуто обосновывать суждения, давать определения, приводить
§25; §44, № 29(а), 48-52(а)
Тема: Построение графиков функций (2 ч).
Цели урока: формирование представлений учащимися о применении производной к исследованию функций и построению графиков; овладение навыками и умениями совершать преобразования графиков; формирование умения применить производную к исследованию функций и построению графиков.
110
Проблемное изложение
Проблемные задачи, фронтальный опрос
Групповая. Составление опорного конспекта, решение задач.
Знают, как применить производную к исследованию функций и построению графиков. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Могут совершать преобразования графиков. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (И)
Самостоятельно искать, извлекать и отбирать необходимую для решения задач информацию
§26; §45, № 1-3(а)
111
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Групповая. Построение алгоритма действия, решение упражнений.
Могут применить производную к исследованию функций и построению графиков. Используют для решения познавательных задач справочную литературу. (П)
Могут совершать преобразования графиков. Могут привести примеры, подобрать аргументы, сформулировать выводы. (ТВ)
Создание компьютерной презентации о построении графика функции
§26; §45, № 4,6,8(а)
Тема: Применение производной для отыскания наибольших и наименьших значений величин (4 ч).
Цели урока: формирование представлений учащимися об исследовании в простейших случаях функции на монотонность; овладение навыками и умениями находить наибольшие и наименьшие значения функций; формирование умения решать задачи на нахождения наибольших и наименьших значений величин.
112
Объяснительно-иллюстративная
Практикум, фронтальный опрос
демонстрация слайд - лекции
Индивидуальная.решение упражнений.
Знают, как исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций. Умеют находить и использовать информацию. (Р)
Могут решать задачи на нахождения наибольших и наименьших значений величин. Умеют составлять текст научного стиля. (И)
Приобретают умения самостоятельной и коллективной деятельности.
§27; §46, № 1-4(а), 9-11(а)
113
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
Групповая. Составление опорного конспекта, решение задач.
Умеют исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций. Могут составить набор карточек с заданиями. (П)
Могут решать задачи на нахождения наибольших и наименьших значений величин. Используют для решения познавательных задач справочную литературу. (И)
Поиск нужной информации в различных источниках
§27; §46, № 12-15(а)
114
Проблемное изложение
Проблемные задачи. Организация совместной деятельности
Групповая. Решение упражнений, ответы на вопросы.
Умеют исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций. Умеют работать с учебником, отбирать материал. (П)
Могут решать задачи на нахождения наибольших и наименьших значений величин. Умеют передавать, информацию сжато, полно, выборочно. (ТВ)
Развитие умения производить рассуждения, проводить обобщение
§27; §46, № 17(а,б), 18(а,б), 30(а)
115
Комбинированная
Практикум, фронтальный опрос
Индивидуальная. Решение упражнений, ответы на вопросы.
Умеют исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функции. Умеют определять понятия, приводить доказательства. (П)
Могут решать задачи на нахождения наибольших и наименьших значений величин. Могут собрать материал для сообщения по заданной теме. (ТВ)
Умение привести примеры, подобрать аргументы.
§46, № 41(а), 35(а)
Контрольная работа №11 (2 ч)
Цель урока проверить знания и умение учащихся по теме применение производной для исследования функций и построение графика функции.
116-117
Урок контроля, оценки и коррекции знаний
Самостоятельное планирование и проведение исследования решения
Индивидуальное решение контрольных заданий.
Учащихся демонстрируют умение расширять и обобщать сведения по исследованию функции, с помощью производной и умение составлять уравнения касательной к графику функции.
Могут строить график функции при полном исследовании функции и совершать преобразования графиков. Могут решать задачи на нахождения наибольших и наименьших значений величин
Владеют навыками самоанализа и самоконтроля
4, 5
проблемные дифференцированные задания.
Комбинаторика и вероятность (9 ч).
Основные цели: создать условия учащимся для:
Формирования представлений о классической вероятностной схеме и классическом определении вероятности; научить решать комбинаторные задачи, познакомить с формулой бинома Ньютона.
Овладения навыками и умениями решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, вычислять коэффициенты бинома Ньютона по формуле.
Тема: Правило умножения. Комбинаторные задачи. Перестановка и факториалы (3ч).
Цели урока: формирование представлений учащимися о правиле умножения, о понятии перестановка и факториал в комбинаторных задачах; овладение навыками и умениями доказательства правила умножения; формирование умения решать комбинаторные задачи.
118
Проблемное изложение
Проблемные задачи, индивидуальный опрос
групповая, индивидуальная. Решение качественных задач.
Могут сформулировать правило умножения; знают понятие перестановка и факториал в комбинаторных задачах. Используют для решения познавательных задач справочную литературу. (Р)
Могут доказать правило умножения. Могут решать комбинаторные задачи. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах.
Уметь составлять текст научного стиля.
§47, №7, 8, 9
119
Комбинированная
Практикум, фронтальный опрос, упражнения
групповая, индивидуальная, работа с раздаточными материалами.
Могут сформулировать правило умножения; знают понятие перестановка и факториал в комбинаторных задачах. Умеют извлекать необходимую информацию из научных текстов. (Р)
Могут доказать правило умножения. Могут решать комбинаторные задачи. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах.
Составление обобщающих информационных таблиц
§47, №11, 12(б), 20
120
Поисковая
Практикум, индивидуальный опрос
групповая, индивидуальная, работа с раздаточными материалами.
Могут сформулировать правило умножения; знают понятие перестановка и факториал в комбинаторных задачах. Могут привести примеры, подобрать аргументы, сформулировать выводы. (П)
Могут доказать правило умножения. Могут решать комбинаторные задачи. Умеют работать с учебником, отбирать и структурировать материал. (ТВ)
Использование справочной литературы, а также материалов ЕГЭ
§48, №3, 5, 6(в,г)
Тема: Выбор нескольких элементов. Биноминальные коэффициенты (3 ч).
Цели урока: формирование представлений учащимися о формуле сочетания и размещения элементов; овладение навыками и умениями применения формулы сочетания и размещения элементов в решении задач; формирование умения решать задачи с выбором большого числа элементов данного множества
121
Проблемное изложение
Проблемные задачи, фронтальный опрос, упражнения
групповая, индивидуальная. Решение качественных задач.
Знают формулу сочетания и размещения элементов и могут их применять в решении задач. Может самостоятельно готовить, проекты, обобщая данные, полученные из различных источников.(Р)
Могут решать задачи с выбором большого числа элементов данного множества. Владение навыками контроля и оценки своей деятельности,
Составление обобщающих информационных таблиц (конспектов)
§48, №3, 5,
122
Комбинированная
Практикум, индивидуальный опрос
групповая, индивидуальная, работа со
сборником задач,
Знают формулу сочетания и размещения элементов и могут их применять в решении задач. Используют для решения задач справочную литературу. (Р)
Могут решать задачи с выбором большого числа элементов данного множества. Умеют работать с учебником, структурировать матер.
Самостоятельно искать необходимую для решения задач
§48, №15, 16
123
Исследовательская
Самостоятельное планирование и проведение исследования
групповая, индивидуальная, работа со сборником задач,
Знают формулу сочетания и размещения элементов и могут их применять в решении задач. Умеют передавать, информацию сжато, полно, выборочно.
Могут решать задачи с выбором большого числа элементов данного множества. Умеют определять понятия, приводить доказательства.
Уметь передавать информацию сжато, полно, выборочно
§48, №6(в,г)
Тема: Случайные события и их вероятности (3ч).
Цели урока: формирование представлений учащимися о классической вероятностной схеме и классическом определении вероятности; формирование умения построить и исследовать учащимися модели различных ситуаций, связанных с понятием случайности
124
Объяснительно-иллюстративная
Самостоятельное планирование и проведение исследования
Фронтальная. Конспектируют лекцию, продумывают примеры.
Знают классическую вероятностную схему и классическое определение вероятности. Умеют извлекать необходимую информацию из учебно-научных текстов. (Р)
Могут построить и исследовать модели различных ситуаций, связанных с понятием случайности. Умеют находить и использовать информацию. (И)
Поиск алгоритмов решения в справочной литературе.
§48, 49
125
Проблемное изложение
Проблемные задачи, фронтальный опрос,
Групповая.решение упражнений.
Знают классическую вероятностную схему и классическое определение вероятности. Умеют определять понятия, приводить доказательства. (П)
Могут построить и исследовать модели различных ситуаций, связанных с понятием случайности (И)
Уметь передавать информацию сжато, полно, выборочно
§49, №3, 4, 6
126
Комбинированная
Практикум, индивидуальный опрос
Индивидуальная, работа с раздаточными материалами.
Знают классическую вероятностную схему и классическое определение вероятности. Могут привести примеры, подобрать аргументы, сформулировать выводы. (П)
Могут построить и исследовать модели различных ситуаций, связанных с понятием случайности. Умеют передавать, информацию сжато, полно, выборочно (ТВ)
Использование для решения познавательных задач справочной литературы
§49, №9, 10
Обобщающее повторение курса алгебры и начала анализа за 10
класс (10 ч).
Основные цели: создать условия учащимся для:
-
Обобщения и систематизации курса алгебры и начала анализа за 10 класса, решая тестовые задания по сборнику Ф.Ф. Лысенко Математика ЕГЭ - 2009, 2011 . Вступительные экзамены.
-
Формирования понимания возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни.
Тема: Числовые функции (1ч).
Цели урока: обобщение и систематизация учащимися свойства числовых функций
127
Комбинированная
Самостоятельное планирование и проведение исследования
Групповая. Решение качественных задач.
Учащихся умеют работать с числовыми функциями, используя их свойства: монотонность, ограниченность сверху и снизу, максимум и минимум, четность и нечетность, периодичность, с обратной функцией. (П)
Учащиеся могут свободно использовать свойства функций для описания функциональной зависимости. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах.
Приведение примеров, подбор аргументов, формулирование выводов
3
Сборник
ЕГЭ
Тема: Тригонометрические функции (1ч).
Цели урока: обобщение и систематизация учащимися тригонометрических функций.
128
Комбинированная
Организация совместной учебной деятельности
Групповая, работа с
сборником задач, ответы на вопросы.
Знают формулу гармонических колебаний и имеют представление о графике гармонических колебаний. Могут собрать материал для сообщения по заданной теме. (Р)
Могут описать колебательный процесс графически. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
Поиск необходимых формул в справочной литературе.
3
Сборник
ЕГЭ
Тема: Тригонометрические уравнения (2ч).
Цели урока: обобщение и систематизация учащимися методов решения тригонометрических уравнений
129
Комбинированная
Самостоятельное планирование и проведение исследования
Групповая. Решение качественных задач.
Умеют преобразовывать простые тригонометрические выражения; решать простые тригонометрические уравнения; решать тригонометрические уравнения. Умеют самостоятельно и мотивированно организовывать свою познавательную деятельность. (П)
Умеют преобразовывать сложные тригонометрические выражения; решать сложные тригонометрические уравнения; вычислять значения выражений с обратными тригонометрическими Функциями.
Объяснение изученных положений на самостоятельно подобранных конкретных примерах
3
Сборник
ЕГЭ
130
Комбинированная
Организация совместной учебной деятельности
Групповая, работа с опорными конспектами, работа с раздаточными материалами.
Умеют преобразовывать простые тригонометрические выражения; решать простые тригонометрические уравнения; решать тригонометрические уравнения; вычислять арксинус, арккосинус, арктангенсчисла. Умеют находить и использовать информацию
Умеют преобразовывать сложные тригонометрические выражения; решать сложные тригонометрические уравнения; вычислять значения выражений с обратными тригонометрическими Функциями.
Поиск необходимых формул в справочной литературе.
3
Сборник
ЕГЭ
Тема: Преобразование тригонометрических выражений (2ч).
Цели урока: обобщение и систематизация учащимися применения формул для преобразования тригонометрических выражений.
131
Комбинированная
Самостоятельное планирование и проведение исследования
Групповая, работа со
сборником задач, ответы на вопросы.
Умеют преобразовывать простые тригонометрические выражения, применяя различные формулы и приемы. Умеют работать с учебником, отбирать и структурировать материал. (П)
Умеют преобразовывать сложные тригонометрические выражения, применяя различные формулы и приемы. Умеют, развернуто обосновывать суждения. (ТВ)
Умение давать определения, приводить доказательства, примеры
3
Сборник
ЕГЭ
132
Комбинированная
Организация совместной учебной деятельности
Групповая, работа с опорными конспектами, с раздаточными материалами.
Умеют преобразовывать простые тригонометрические выражения, применяя различные формулы и приемы. Умеют определять понятия, приводить доказательства. Умеют находить и использовать информацию. (П)
Умеют преобразовывать сложные тригонометрические выражения, применяя различные формулы и приемы. Могут составить набор карточек с заданиями (И)
Поиск необходимых формул в справочной литературе.
3
Сборник
ЕГЭ
Тема: Применение производной (2ч).
Цели урока: обобщение и систематизация учащимися применение производной в исследовании функции и построения графика этой функции
133
Комбинированная
Самостоятельное планирование и проведение исследования
Групповая, работа со
сборником задач, ответы на вопросы.
Могут использовать производную для нахождения наилучшего решения в прикладных, в том числе социально - экономических, задачах (П)
Могут находить скорости для процесса, заданного формулой или графиком. Умеют работать с учебником, отбирать и структурировать материал. (ТВ)
Умение развернуто давать доказательства
3
Сборник
ЕГЭ
134
Комбинированная
Организация совместной учебной деятельности
Групповая. Решение качественных задач.
Могут использовать производную для нахождения наилучшего решения в прикладных, в том числе социально - экономических, задачах. (П)
Могут находить скорости для процесса, заданного формулой или графиком. Используют для решения задач справочную литературу. (И)
Поиск необходимых формул в справочной литературе.
3
Сборник
ЕГЭ
Итоговая контрольная работа по алгебре и началам анализа (2 ч).
Цель урока проверить знания и умения, учащихся по курсу 10-го класса.
135-136
Урок обобщения и систематизации знаний
Самостоятельное планирование и проведение исследования решения
Индивидуальное решение контрольных заданий.
Проверить умение обобщения и систематизации знаний по основным темам курса математики 10 класса
Проверить умение обобщения и систематизации знаний по задачам повышенной сложности
Владеют навыками самоанализа и самоконтроля
4, 5
проблемные дифференцированные задания.
Календарно-тематическое планирование уроков геометрии на
2015_ / 2016_ учебный год.
Класс: 10
Учитель Асташенко Светлана Анатольевна
Количество часов:
-
на учебный год: 68
-
в неделю: 2
Плановых контрольных уроков:
I полугодие 2
II полугодие 3
Итого: 5
Планирование составлено на основе: Программы для общеобразовательных школ, гимназий, лицеев: Математика, 5 - 11 кл. / Сост. Г.М. Кузнецова, Н.Г. Миндюк. / 4-е изд., стереотип. М.: Дрофа, 2009. - 320с.
Учебник: Геометрия, 10 - 11. / А.С. Атанасян, В.Ф. Бутузов и др. / М.: Просвещение, 2011 - 2015.
Дополнительная литература:
-
Дидактические материалы по геометрии для 10 класса. / Б.Г. Зив. / М. Просвещение, 2011.
-
Задачи по геометрии для 7 - 11 классов. , Б.Г. Зив, В.М. Мейлер, А.П. Баханский. / М.: Просвещение, 2010.
-
Изучение геометрии в 10 - 11 классах: Методические рекомендации к учебнику. Книга для учителя. / С.М. Саакян, В.Ф. Бутузов. / М.: Просвещение, 2011.
п/п
Раздел, название урока в
поурочном планировании
Дидактические единицы образовательного процесса
Контроль
знаний
учащихся
Коли-
чество
часов
Дата
Корректи-
ровка
I полугодие 32
ВВЕДЕНИЕ.
Основная цель введения: сформировать представления учащихся об основных понятиях и аксиомах стереометрии, их использовании при решении стандартных задач
логического характера, а также об изображениях точек, прямых и плоскостей на проекционном чертеже при различном их взаимном расположении в пространстве.
Уроки - практикумы по решению задач.
1
Предмет стереометрии. Аксиомы стереометрии, п.1, 2.
Знать и понимать:
Основные свойства плоскости.
Некоторые следствия из аксиом.
Уметь:
Применять аксиомы стереометрии и некоторые их следствия к решению задач.
Комбинированный урок. Урок - практикум по решению задач.
1
2
Некоторые следствия из аксиом, п.3.
Урок - практикум по решению задач.
1
ГЛАВА I. Параллельность прямых и плоскостей
Основная цель: дать учащимся систематические сведения о параллельности прямых и плоскостей в пространстве.
19
§1. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ.
Знать и понимать:
Основные свойства плоскости.
Некоторые следствия из аксиом.
Взаимное расположение двух прямых в пространстве.
Понятие параллельных и скрещивающихся прямых..
Лемма о пересечении плоскости параллельными прямыми, теорема о трех параллельных прямых].
Взаимное расположение прямой и плоскости в
пространстве.
Понятие параллельности прямой и плоскости Признак параллельности прямой и плоскости.
Признак скрещивающихся прямых.
Свойства параллельных плоскостей.
Теорема существования и единственности плоскости, параллельной данной и проходящей через данную точку пространства.
Теорема об углах с сонаправленными сторонами.
Понятие параллельных плоскостей, признак параллельности двух плоскостей.
Теорему о проведении через одну из
скрещивающихся прямых плоскости, параллельной
другой прямой.
3
Параллельные прямые в пространстве, п.4.
Изучение и первичное закрепление новых знаний (беседа); Групповой контроль.
1
4
5
Параллельность трех прямых. Параллельность прямой и плоскости, п. 5, 6.
Усвоение изученного материала в процессе решения задач. Самоконтроль, ИК
2
6
ЗАЧЕТ №1 «ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ»
Урок - зачет.
1
§2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ.
l
№
п/п
Раздел, название урока в
поурочном планировании
Дидактические единицы образовательного процесса
Контроль
знаний
учащихся
Коли-
чество
часов
Дата
Корректи-
ровка
7
Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых
плоскости, параллельной другой прямой, п.7.
Уметь:
Доказывать основные теоремы.
Применять метод доказательства от противного при решении задач и доказательстве теорем.
Применять изученную теорию к решению задач.
Применять аксиомы стереометрии и их
следствий к решению задач.
Изображать пространственные фигуры на
плоскости.
Изображать параллельные прямые, параллельные прямую и плоскость, параллельные плоскости в пространстве.
Иллюстрировать изученные понятия, связанные со взаимным расположением прямых и плоскостей на примере треугольной пирамиды.
Урок лекция с необходимым минимумом задач.
1
8
Угол с сонаправленными сторонами, п 8.
Обучающий, тест. Решение задач.
1
9
Угол между прямыми, п 9.
Урок усвоения новых знаний, умений и навыков.
1
10
Решение задач.
Урок обобщения и систематизации знаний. Практикум по решению задач. Групповой, устный контроль.
1
11
Контрольная работа №1 «ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ» п.1 - 9.
Уметь:
Применять аксиомы стереометрии и их
следствий к решению задач.
Применять изученную теорию к решению задач.
Урок контроля, оценки и коррекции знаний учащихся. Фронтальный тематический контроль.
1
§3. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ.
Знать и понимать:
Понятие параллельных плоскостей, признак параллельности двух плоскостей.
Теорема существования и единственности плоскости,
параллельной данной и проходящей через данную
точку пространства.
Свойства параллельных плоскостей.
Тетраэдр, параллелепипед. Свойства ребер, граней, диагоналей параллелепипеда.
Способы изображения пространственных фигур
на плоскости.
Понятие сечения фигур.
Понятие прямоугольного параллелепипеда.
Свойство диагоналей прямоугольного параллелепипеда.
l
12
Параллельные плоскости. Признак параллельности двух плоскостей, п.10.
Урок усвоения новых знаний, умений и навыков.
1
13
Свойства параллельных плоскостей, п.11.
Обучающий, тест. Решение задач.
1
14
Параллельность плоскостей. Свойства параллельных плоскостей, п.10, 11.
Решение задач. С/Р Индивидуальный контроль.
1
15
ЗАЧЕТ №2 «ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ»
Урок - зачет. Закрепление пройденного материала
1
§4. ТЕТРАЭДР И ПАРАЛЛЕЛЕПИПЕД.
№
п/п
Раздел, название урока в
поурочном планировании
Дидактические единицы образовательного процесса
Контроль
знаний
учащихся
Коли-
чество
часов
Дата
Корректи-
ровка
16
Тетраэдр, п.12.
Уметь:
Изображать пространственные фигуры на
плоскости.
Решать задачи на построение сечений тетраэдра и параллелепипеда.
Урок лекция с необходимым минимумом задач.
1
17
Параллелепипед. Свойства граней и диагоналей параллелепипеда, п. 13.
Урок лекция с необходимым минимумом задач.
1
18
19
20
Задачи на построение сечений тетраэдра и параллелепипеда, п.14
Урок обобщения и систематизации знаний. Практикум по решению задач. Групповой, устный контроль.
3
21
Контрольная работа №2 «ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ. ТЕТРАЭДР. ПАРАЛЛЕЛЕПМПЕД», п.10 - 14.
Уметь: применять теоретический материал при решении задач.
Урок контроля, оценки и коррекции знаний учащихся. Фронтальный тематический контроль.
1
ГЛАВА II. Перпендикулярность прямых и плоскостей
Основная цель главы II: дать учащимся систематические сведения о перпендикулярности прямых и плоскостей в пространстве, ввести понятие углов между прямыми и плоскостями, между плоскостями.
16
§1. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ.
Знать и понимать:
Метод доказательства от противного.
Лемма о перпендикулярности двух параллельных прямых к третьей прямой.
Определение прямой, перпендикулярной к
плоскости.
Признак перпендикулярности прямой и
плоскости.
Теоремы о существовании и единственности прямой (плоскости), перпендикулярной к данной плоскости (прямой).
Понятие расстояния от точки до плоскости,
перпендикуляра к плоскости из точки,
наклонной, проведенной из точки к плоскости, основания наклонной, проекции наклонной.
Теорема о тех перпендикулярах.
22
Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости, п.15, 16.
Обучающий урок.
Самостоятельная работа
1
23
Признак перпендикулярности прямой и плоскости. Теорема о прямой, перпендикулярной к плоскости п.17, 18.
Обучающий урок.
Самостоятельная работа
1
24
25
Перпендикулярность прямых и плоскостей, п.15-18.
Закрепление пройденного материала. Практикум по решению задач. Проверочная С/Р. Индивидуальный контроль.
2
№
п/п
Раздел, название урока в
поурочном планировании
Дидактические единицы образовательного процесса
Контроль
знаний
учащихся
Коли-
чество
часов
Дата
Корректи-
ровка
§2. ПЕРПЕНДИКУЛЯР И НАКЛОННЫЕ.
Связь между наклонной, её проекцией и
перпендикуляром.
Уметь:
Применять изученную теорию к решению за-
дач.
Доказывать основные теоремы.
Находить угол между прямой и плоскостью,
между плоскостями.
m
26
Расстояние от точки до плоскости. Теорема о трех перпендикулярах, п.19, 20.
Изучение и первичное закрепление новых знаний (беседа); Групповой контроль.
1
27
Угол между прямой и плоскостью, п.21.
Комбинированный урок. Урок - практикум по решению задач.
1
28
29
Теорема о трех перпендикулярах. Угол между прямой и плоскостью, п.19-21.
Комбинированный урок. Урок - лекция, элементы исследовательской деятельности.
2
30
ЗАЧЕТ №3 «ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ»
Урок - зачет Тематический фронтальный контроль.
1
§3. ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ.
Знать и понимать:
Определение двугранного угла.
Свойство двугранного угла, часто применяющееся при решении задач.
Геометрическую интерпретацию угла между прямой и плоскостью, двугранного и
линейного угла.
Определение перпендикулярных плоскостей.
m
31
Двугранный угол. Линейный угол двугранного угла, п.22.
Комбинированный урок: лекция, практическая работа.
1
32
Признак перпендикулярности двух плоскостей, п.23.
Усвоение нового материала в процессе решения задач. С/Р обучающего характера с проверкой на уроке.
1
II полугодие 36
33
Прямоугольный параллелепипед. Свойство диагоналей прямоугольного параллелепипеда, п.24.
Признак перпендикулярности плоскостей.
Понятие прямоугольного параллелепипеда.
Свойство диагоналей прямоугольного параллелепипеда.
Усвоение нового материала в процессе решения задач. Самоконтроль.
1
34
Перпендикулярность прямых и плоскостей, перпендикулярность плоскостей (зачет).
Практикум по решению задач. Проверочная С/Р.
1
№
п/п
Раздел, название урока в
поурочном планировании
Дидактические единицы образовательного процесса
Контроль
знаний
учащихся
Коли-
чество
часов
Дата
Корректи
ровка
35
36
Решение задач.
Уроки обобщения и систематизации знаний. Практикум по решению задач. Групповой, устный контроль
2
37
Контрольная работа №3 «ПЕРПЕНДИКУЛЯРНОСТЬ В ПРОСТРАНСТВЕ», п.15 - 24.
Уметь применять изученный теоретический материал при выполнении письменной работы.
Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль.
1
ГЛАВА III. Многогранники
Основная цель главы II: дать учащимся систематические сведения о перпендикулярности прямых и плоскостей в пространстве, ввести понятие углов между прямыми и плоскостями, между плоскостями.
16
§1. ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА.
Знать и понимать:
Понятие многогранника, основные виды
многогранников, изображение многогранников на плоскости.
Призмы и их элементов, виды призм.
Формулу для вычисления площади боковой
поверхности прямой призмы.
Формулу для вычисления площади боковой
поверхности наклонной призмы.
Понятие пирамиды, правильной пирамиды,
усеченной пирамиды.
Формулу для вычисления площади полной
поверхности пирамиды.
Свойства пирамид, имеющих равные боковые ребра; равные апофемы.
Понятие правильного многогранника.
38
Понятие многогранника. Геометрическое тело. Призма (определение, элементы), п.25-27.
Комбинированный урок: лекция, практическая работа.
1
39
Виды призм. Площадь поверхности прямой призмы, п.27.
Практический урок + объяснение.
Проверочная работа
1
40
Наклонная призма. Площадь поверхности наклонной призмы, п.27.
Усвоение изученного материала в процессе решения задач С/Р.
1
41
Построение сечений призмы.
Комбинированный урок: лекция, практическая работа.
1
§2. ПИРАМИДА.
42
Пирамида. Площадь полной поверхности пирамиды, п.28.
Лекция
1
43
Правильная пирамида. Площадь боковой поверхности правильной пирамиды, п.29.
Изучение и первичное закрепление новых знаний.
1
№
п/п
Раздел, название урока в
поурочном планировании
Дидактические единицы образовательного процесса
Контроль
знаний
учащихся
Коли-
чество
часов
Дата
Корректи
ровка
44
Ключевые задачи. Свойства пирамид, имеющих равные боковые ребра; равные апофемы, п.28-30.
Знать и понимать:
Понятие многогранника, основные виды
многогранников, изображение многогранников на плоскости.
Призмы и их элементов, виды призм.
Формулу для вычисления площади боковой
поверхности прямой призмы.
Формулу для вычисления площади боковой
поверхности наклонной призмы.
Понятие пирамиды, правильной пирамиды,
усеченной пирамиды.
Формулу для вычисления площади полной
поверхности пирамиды.
Свойства пирамид, имеющих равные боковые ребра; равные апофемы.
Понятие правильного многогранника.
Уметь:
Применять изученную теорию к решению задач.
Выводить формулы.
Комбинированные уроки: лекция, практикум, проверочная С/Р.
1
45
Усеченная пирамида. Площадь боковой поверхности усеченной пирамиды, п.30.
Урок контроля, оценки и коррекции знаний. Фронтальный письменный контроль.
1
46
Пирамида, п.28-30.
Практический урок + объяснение.
Самостоятельная работа.
1
§3. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ.
47
Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников, п.31-33.
Комбинированные уроки: лекция, практикум, обучающая С/Р.
1
48
Правильные многогранники, п.31-33.
Исследовательская деятельность.
1
49
ЗАЧЕТ №4 «МНОГОГРАННИКИ»
Урок - зачет.
Урок контроля, оценки и коррекции знаний. Фронтальный устный контроль.
1
50
51
52
Решение задач.
Усвоение изученного материала в процессе решения задач.
3
53
Контрольная работа №4 «МНОГОГРАННИКИ», п.25 - 33.
Уметь применять изученный теоретический материал при выполнении письменной работы.
Урок контроля, оценки и коррекции знаний. Фронтальный письменный контроль
1
№
п/п
Раздел, название урока в
поурочном планировании
Дидактические единицы образовательного процесса
Контроль
знаний
учащихся
Коли-
чество
часов
Дата
Корректи
ровка
ГЛАВА IV. Векторы в пространстве
Основная цель главы IV: обобщить изученный в базовой школе материал о векторах на плоскости, дать систематические сведения о действиях с векторами в пространстве.
11
§1. ПОНЯТИЕ ВЕКТОРА В ПРОСТРАНСТВЕ.
Знать и понимать:
Понятие вектора на плоскости (из курса
базовой школы).
Понятие вектора в пространстве.
Правила сложения, вычитания и умножения вектора на число.
Понятие компланарных векторов.
Правило сложения для трех некомпланарных
векторов (правило параллелограмма).
Теорема о разложении любого вектора по
трем некомпланарным векторам.
Уметь:
Использовать векторный метод при решении задач.
Выполнять действия над векторами в пространстве.
Раскладывать вектор по трем некомпланарным векторам.
Доказывать теоремы.
54
55
Понятие вектора. Длина вектора. Коллинеарные векторы. Равенство векторов, п.34, 35.
Практический урок + объяснение.
2
§2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО.
56
Сложение и вычитание векторов. Сумма нескольких векторов, п.36, 37.
Изучение нового материала. Урок с частично- поисковой деятельностью Проверочная С/Р.
1
57
Умножение вектора на число, п.38. Действия над векторами, п.34-38.
Урок обобщения и систематизации знаний. Практикум по решению задач. Групповой, устный и письменный контроль.
1
§3. КОМПЛАНАРНЫЕ ВЕКТОРЫ.
58
Компланарные векторы, п.39.
Комбинированный урок Усвоение изученного материала в процессе решения задач. Практическая работа.
1
59
Правило сложения трех некомпланарных векторов (правило параллелепипеда), п.40.
Объяснение нового материала.
Закрепление пройденного материала. С/Р.
1
№
п/п
Раздел, название урока в
поурочном планировании
Дидактические единицы образовательного процесса
Контроль
знаний
учащихся
Коли-
чество
часов
Дата
Корректи
ровка
60
Разложение вектора по трем некомпланарным векторам, п.41.
Изучение нового материала. Урок с частично- поисковой деятельностью Проверочная С/Р.
1
61
ЗАЧЕТ №5 «ВЕКТОРЫ В ПРОСТРАНСТВЕ»
Урок - зачет.
1
62
63
Решение задач.
Урок обобщения и систематизации знаний. Практикум по решению задач.
2
64
Контрольная работа №5 «ВЕКТОРЫ В ПРОСТРАНСТВЕ», п.34-41.
Урок контроля, оценки и коррекции знаний учащихся.Тематический индив. контроль.
1
Итоговое повторение.
Основная цель: систематизировать, повторить, закрепить, проверить знания, умения и навыки учащихся по изученному материалу.
4
65
66
67
68
Повторение материала, изученного в курсе геометрии 10 класса.
Уметь применять изученный теоретический материал при выполнении письменной работы.
Уроки обобщения и систематизации изученного материала.
4
п/п
8-9
10
3
4
5
6
7
Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.
Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
-
работа выполнена полностью;
-
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
-
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
-
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
-
допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
-
допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
-
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
-
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
-
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
-
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
-
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
-
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
-
отвечал самостоятельно, без наводящих вопросов учителя;
-
возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
-
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
-
допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
-
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
-
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
-
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
-
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
-
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
-
не раскрыто основное содержание учебного материала;
-
обнаружено незнание учеником большей или наиболее важной части учебного материала;
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
-
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
-
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
-
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
-
незнание наименований единиц измерения;
-
неумение выделить в ответе главное;
-
неумение применять знания, алгоритмы для решения задач;
-
неумение делать выводы и обобщения;
-
неумение читать и строить графики;
-
неумение пользоваться первоисточниками, учебником и справочниками;
-
потеря корня или сохранение постороннего корня;
-
отбрасывание без объяснений одного из них;
-
равнозначные им ошибки;
-
вычислительные ошибки, если они не являются опиской;
-
логические ошибки.
К негрубым ошибкам следует отнести:
-
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
-
неточность графика;
-
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
-
нерациональные методы работы со справочной и другой литературой;
-
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
-
нерациональные приемы вычислений и преобразований;
-
небрежное выполнение записей, чертежей, схем, граф
УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
Учебные пособия
-
Атанасян Л.С., Бутузов В.Ф, Кадамцева С.Б. и др. Геометрия. 10-11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни. - М. Просвещение, 2010
-
Мордкович, А.Г., Семенов П.В. Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) - М.: Мнемозина, 2011
-
Мордкович и др. Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений (профильный уровень) - М.: Мнемозина, 2011
-
Мордкович, А.Г., Семенов П.В. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) - М.: Мнемозина, 2012
-
Мордкович и др. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений (профильный уровень) - М.: Мнемозина, 2012
Методические пособия
-
Мордкович, А.Г., Семенов П.В. Алгебра и начала математического анализа. 10 класс. Методическое пособие для учителя (профильный уровень) - М.: Мнемозина, 2010
-
Мордкович, А.Г., Семенов П.В. Алгебра и начала математического анализа. 11 класс. Методическое пособие для учителя (профильный уровень) - М.: Мнемозина, 2010
-
Саакян С.М., Бутузов В.Ф. Изучение геометрии в 10-11 классах: методические рекомендации к учебнику: книга для учителя. - М.: Просвещение, 2004
Дидактический материал
-
Александрова Л.А. Алгебра и начала математического анализа. 10 класс. Самостоятельные работы (профильный уровень). - М.: Мнемозина, 2012
-
Александрова Л.А. Алгебра и начала математического анализа. 11 класс. Самостоятельные работы (профильный уровень). - М.: Мнемозина, 2012
-
Глизбург В.И. Алгебра и начала анализа. Контрольные работы для 10 класса общеобразовательных учреждений (профильный уровень). - М.: Мнемозина, 2007
-
Глизбург В.И. Алгебра и начала анализа. Контрольные работы для 11 класса общеобразовательных учреждений (профильный уровень). - М.: Мнемозина, 2008
-
Зив Б.Г. Дидактические материалы по геометрии для 10 класса. - М.: Просвещение, 2009
-
Зив Б.Г. Дидактические материалы по геометрии для 11 класса. - М.: Просвещение, 2008
Литература для обучающихся
-
Жафяров А.Ж. Обучающий задачник. Математика 10-11 классы. Профильный уровень. - М.: Просвещение, 2006 г.
-
Математика. Подготовка к ЕГЭ-2012. Элементы теории вероятностей и статистики: учебное пособие / Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. - Ростов-на-Дону: Легион-М, 2011 - 32 с. - (Готовимся к ЕГЭ)
-
Математика. Учимся решать задачи с параметром. Подготовка к ЕГЭ: задание С5 / Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. - Ростов-на-Дону: Легион-М, 2011 - 48 с. - (Готовимся к ЕГЭ)
-
ЕГЭ: 3000 задач с ответами по математике. Все задания группы В / Под ред. А.Л. Семенова, И.В. Ященко. - М.: Изд-во «Экзамен», 2011 - 511 с. (Серия «Банк заданий ЕГЭ»)
-
Общие подходы к решению уравнений: Учебное пособие / Под ред. Н.А. Цыпленковой. - Вологда: ВГПУ, изд-во «Русь», 2004. - 36 с. (Серия: Профильное обучение. Математика. Выпуск №3)
-
Основные методы и приемы решения целых рациональных уравнений: Учебное пособие / Под ред. Н.А. Цыпленковой. - Вологда: ВГПУ, изд-во «Русь», 2004. - 36 с. (Серия: Профильное обучение. Математика. Выпуск №4)
-
Использование понятия модуля в тождественных преобразованиях выражений: Учебное пособие / Под ред. Н.А. Цыпленковой. - Вологда: ВГПУ, изд-во «Русь», 2005. - 30 с. (Серия: Профильное обучение. Математика. Выпуск №5)
Электронные ресурсы
-
Открытый банк задач ЕГЭ по математике - Режим доступа: mathege.ru
-
ЕГЭ-2013: математика. Задачи. Ответы. Решения. Обучающая система Дмитрия Гущина «Решу ЕГЭ» - режим доступа: reshuege.ru
-
Онлайн-подготовка к ЕГЭ и ГИА - Режим доступа: ege.yandex.ru</</p>
6. Контрольные работы по алгебре
Контрольная работа № 1 (1 час)
Вариант 1
-
Найдите остаток от деления на 11 числа 437.
-
Запишите периодическую дробь 0,(87) в виде обыкновенной дроби.
-
Сравните числа
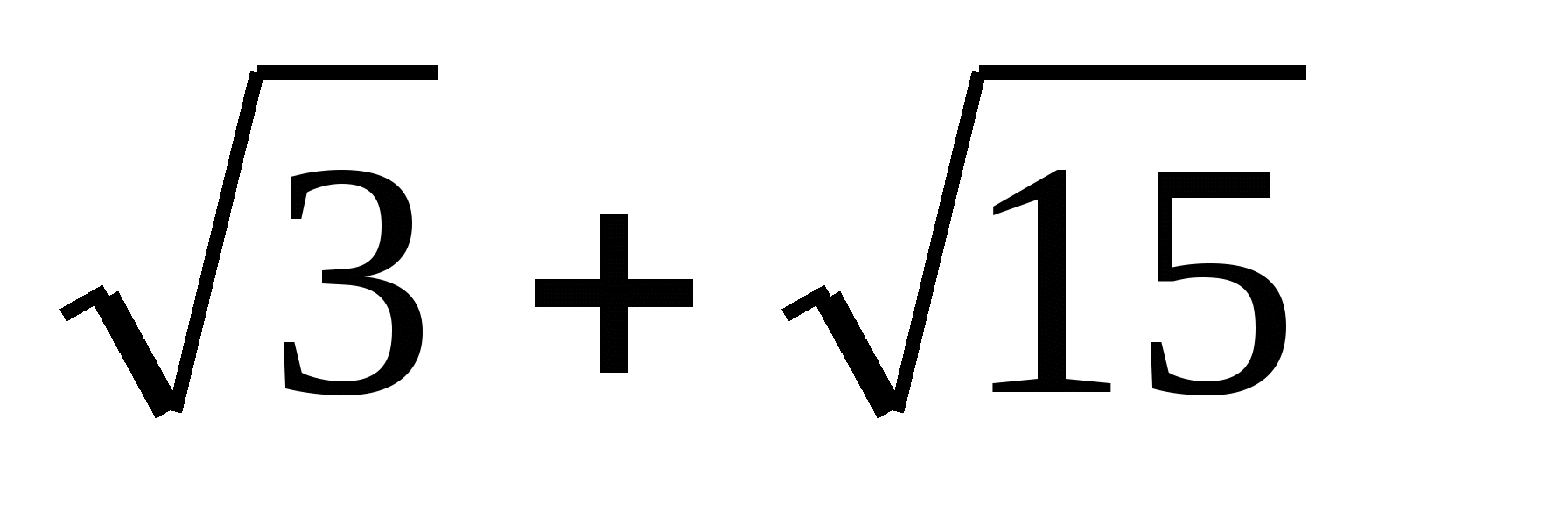 и
и 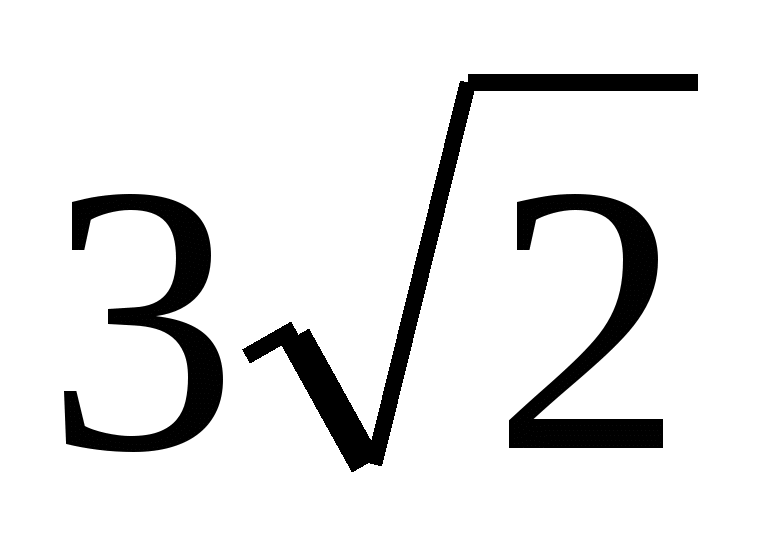 .
.
-
Решите уравнение
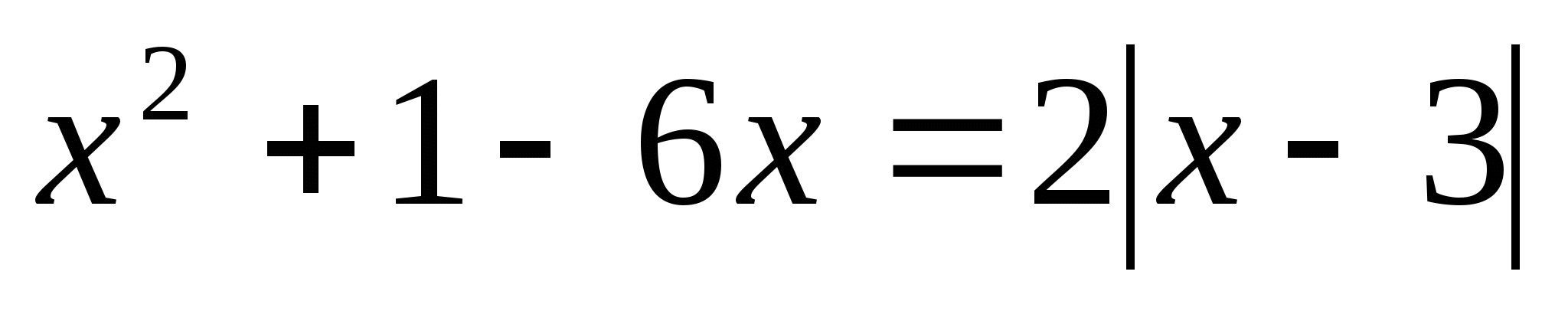 .
.
____________________________________________________
5. Решите неравенство ![]() .
.
_____________________________________________________
6. Постройте график функции ![]() .
.
Вариант 2
-
Найдите остаток от деления на 19 числа 671.
-
Запишите периодическую дробь 0,(35) в виде обыкновенной дроби.
-
Сравните числа
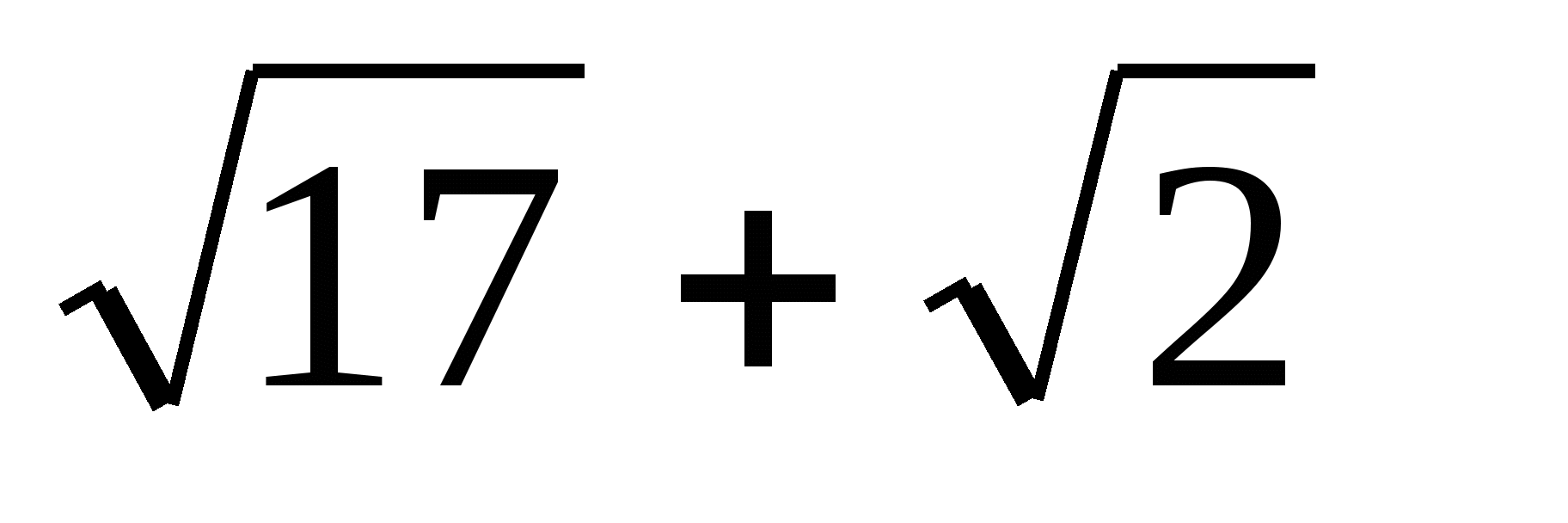 и
и 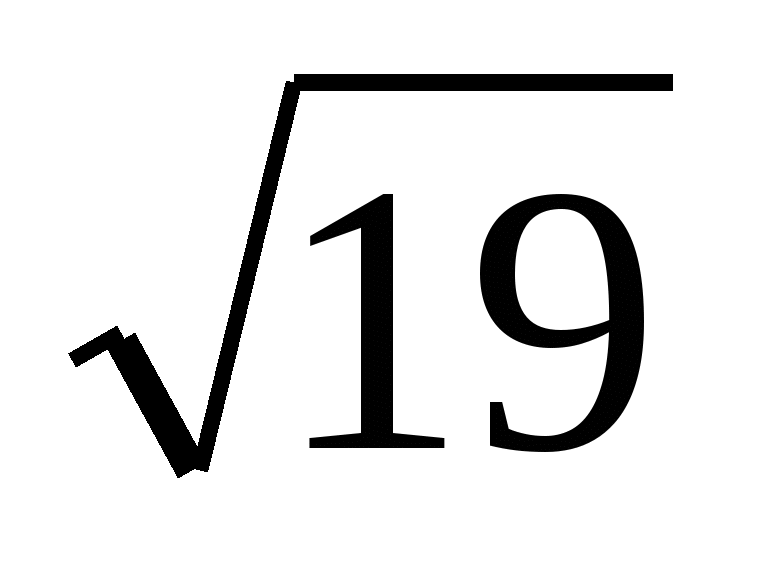 .
.
-
Решите уравнение
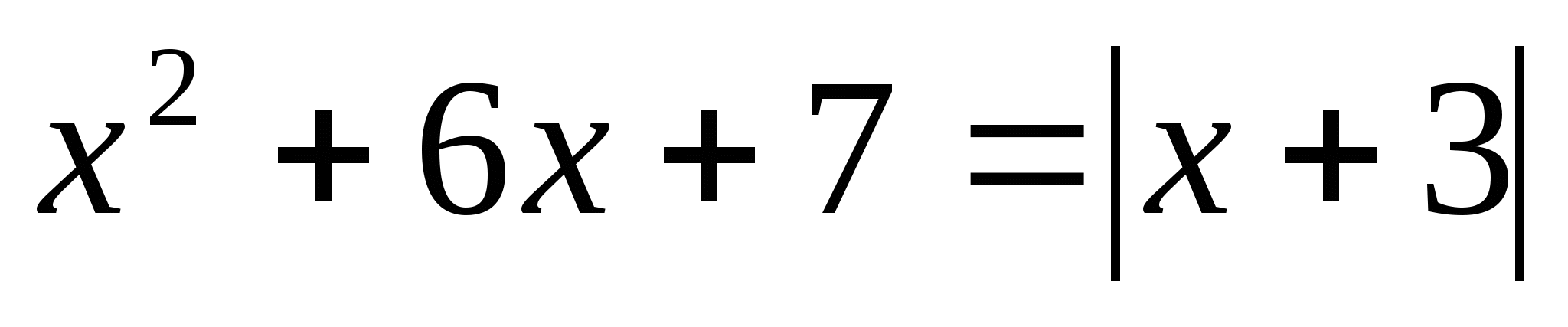 .
.
_______________________________________________________
5. Решите неравенство ![]() .
.
_______________________________________________________
6. Постройте график функции ![]() .
.
Контрольная работа № 2 (2 час)
Вариант 1
-
Задает ли указанное правило функцию
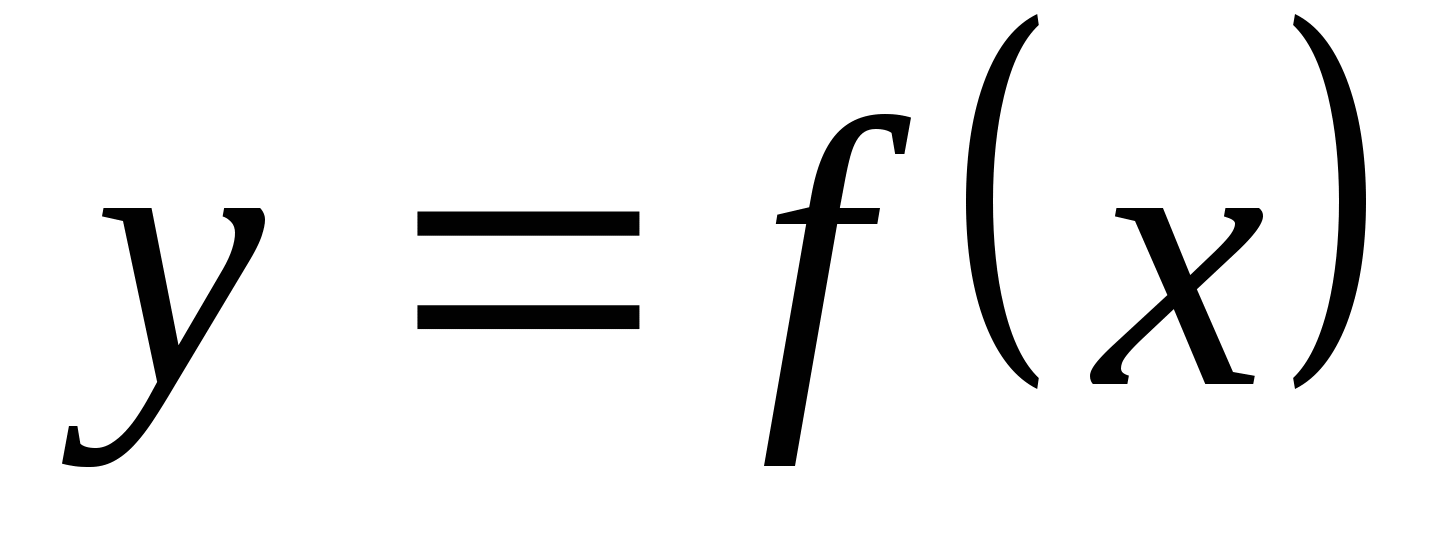 , если:
, если:
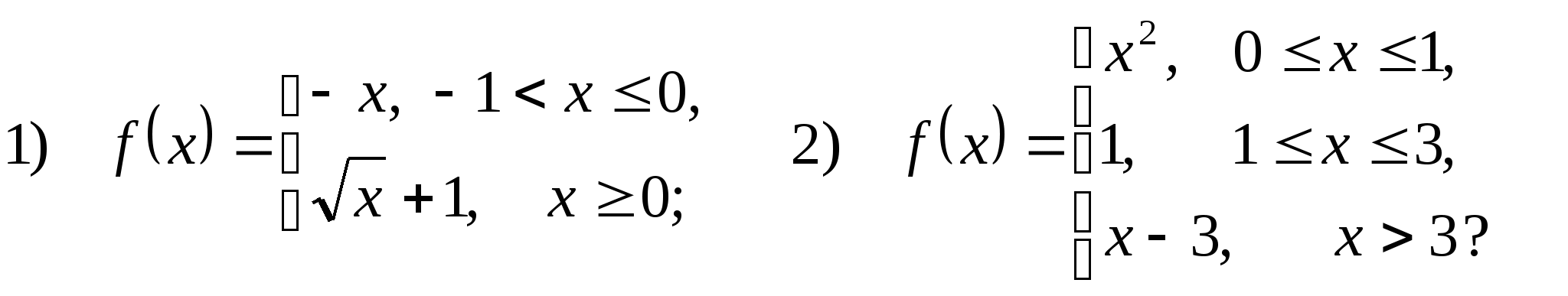
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках ─ 2; 1; 5;
в) постройте график функции;
г) найдите промежутки монотонности функции.
-
Исследуйте функцию
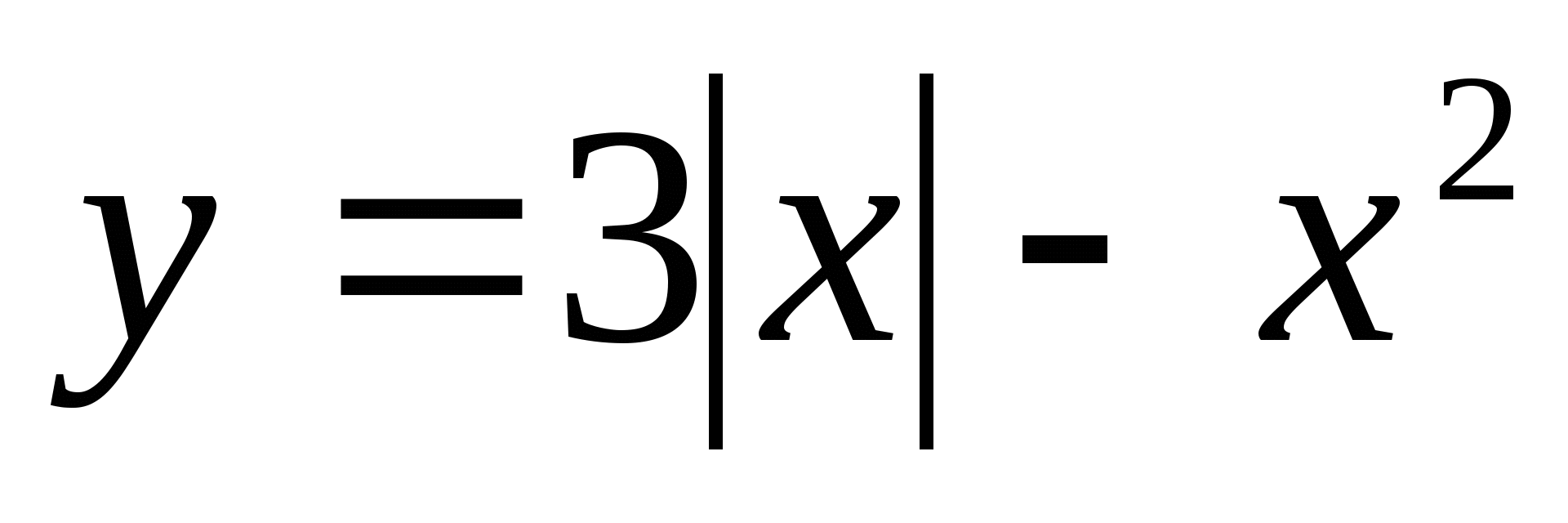 на
четность.
на
четность.
-
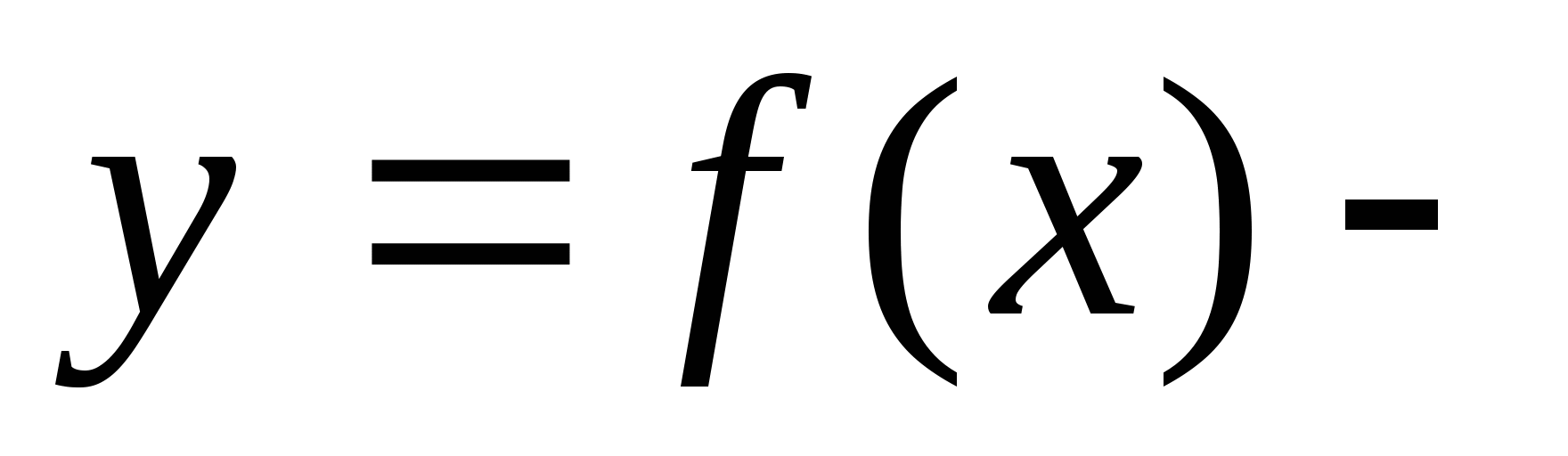 периодическая функция с
периодомТ = 3. Известно, что
периодическая функция с
периодомТ = 3. Известно, что
![]()
а) Постройте график функции;
б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
-
Придумайте пример аналитически заданной функции, определенной на открытом луче
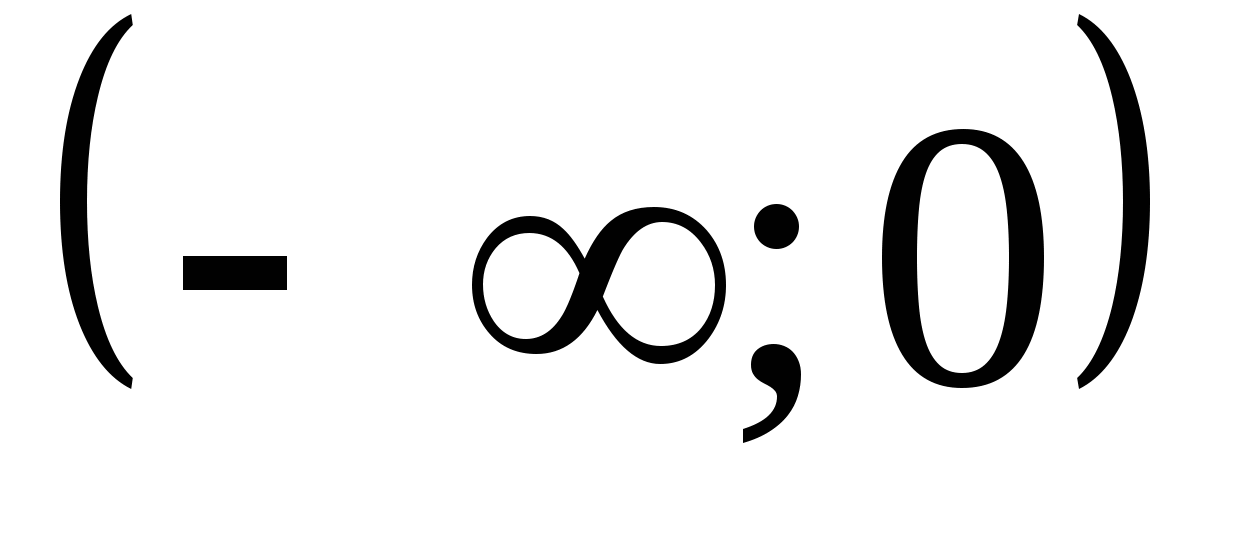 .
.
-
Известно, что функция
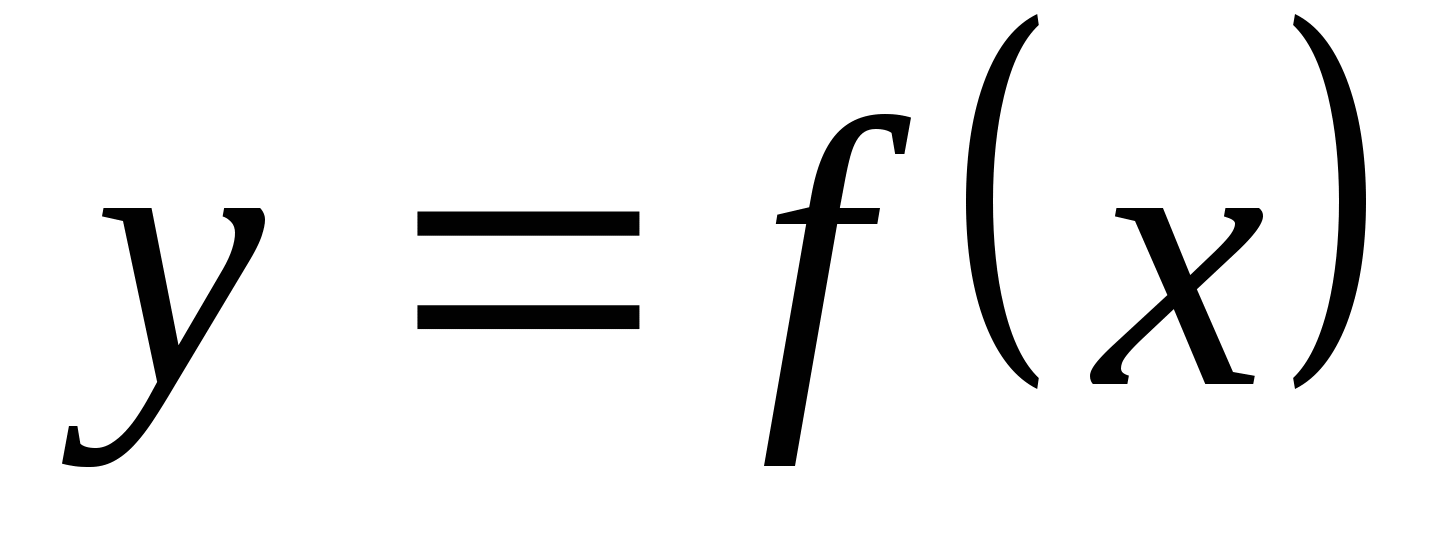 возрастает на R. Решите неравенство
возрастает на R. Решите неравенство
![]() .
.
______________________________________________________________
6. Найдите функцию, обратную функции ![]() . Постройте
. Постройте
на одном чертеже графики указанных двух взаимно обратных функций.
______________________________________
7. Вычислите: ![]() .
.
Вариант 2
-
Задает ли указанное правило функцию
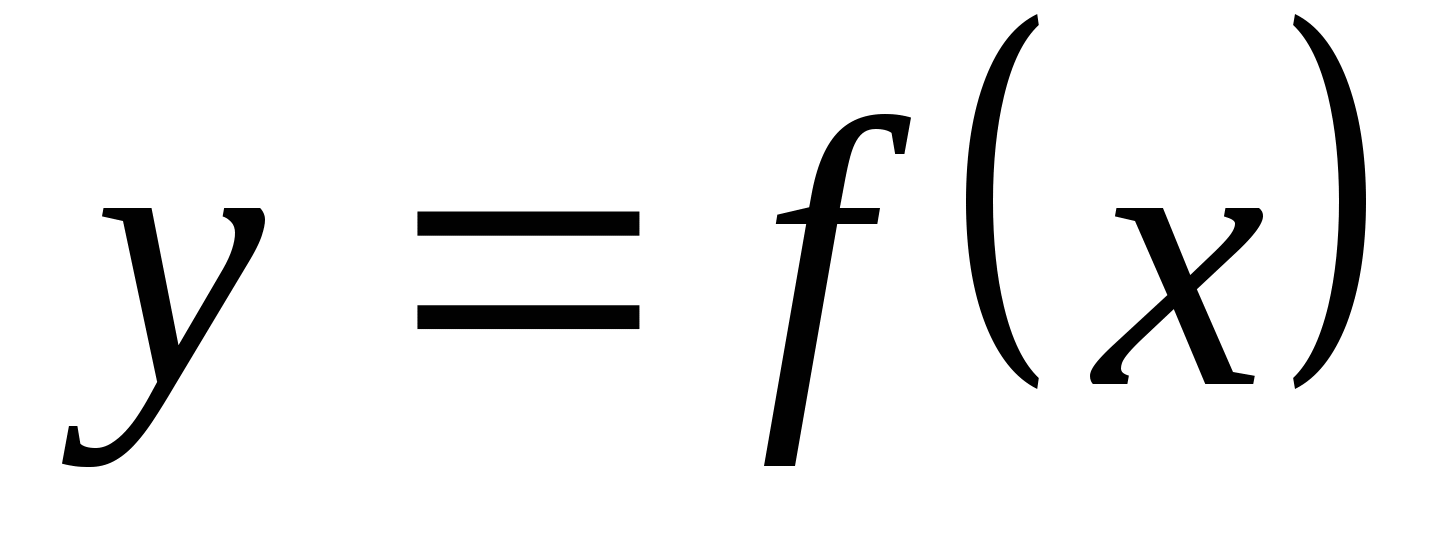 , если:
, если:
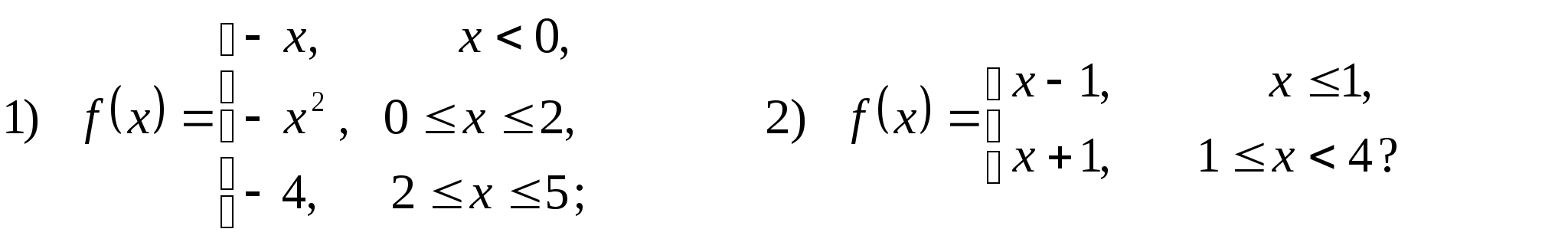
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках ![]() ; 2; 6;
; 2; 6;
в) постройте график функции;
г) найдите промежутки монотонности функции.
-
Исследуйте функцию
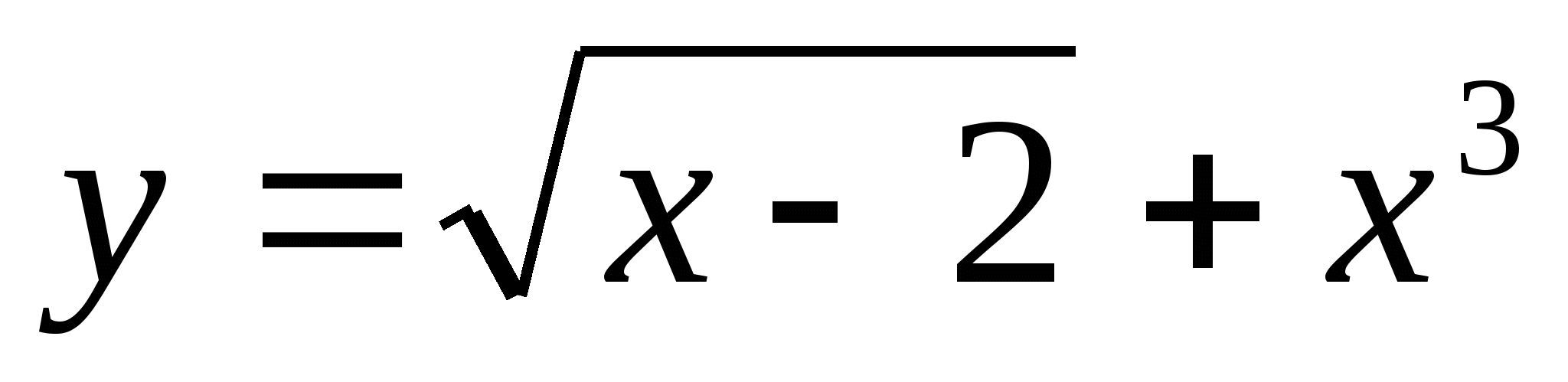 на
четность.
на
четность.
-
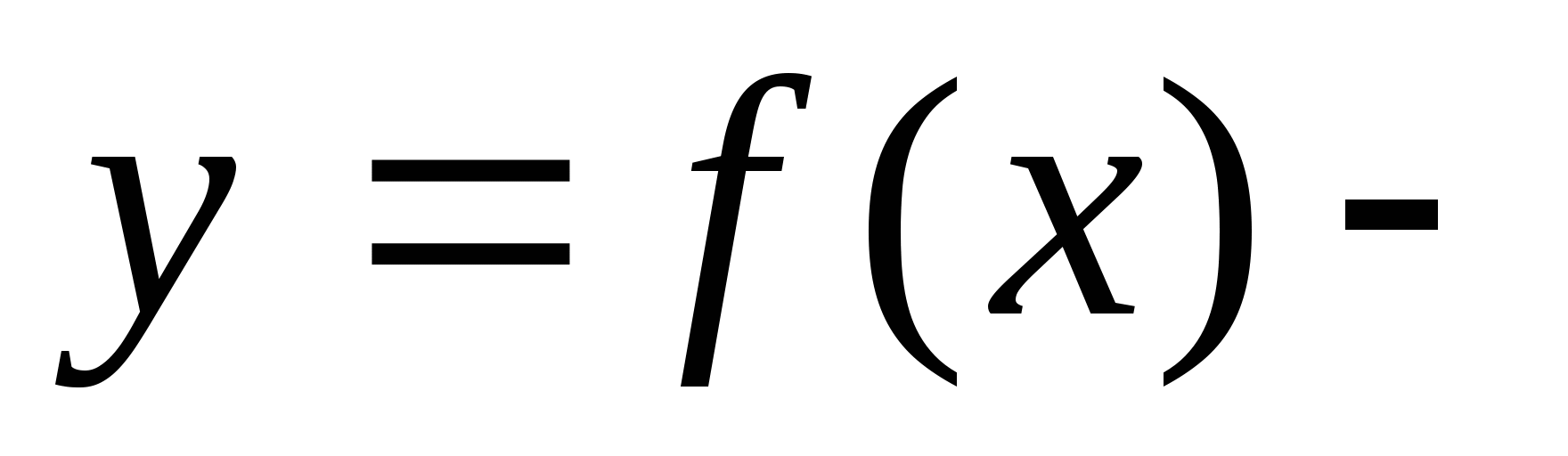 периодическая функция с
периодомТ = 2. Известно, что
периодическая функция с
периодомТ = 2. Известно, что 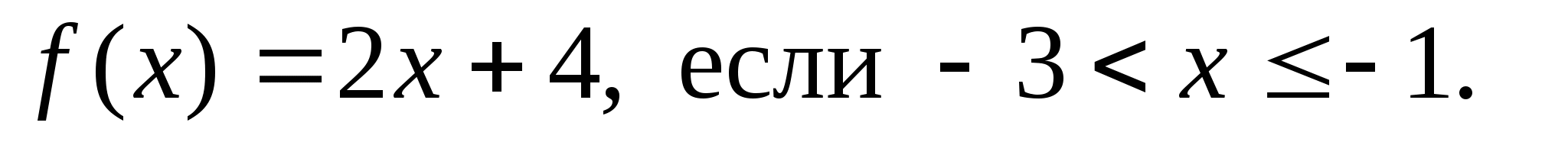
а) Постройте ее график функции;
б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
-
Придумайте пример аналитически заданной функции, определенной на луче
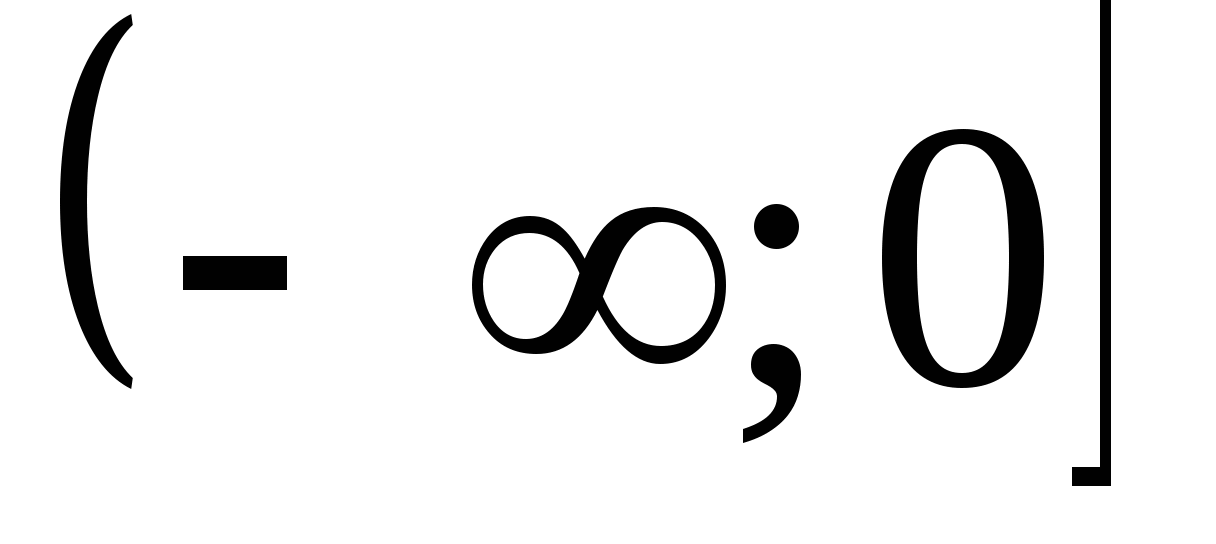 .
.
-
Известно, что функция
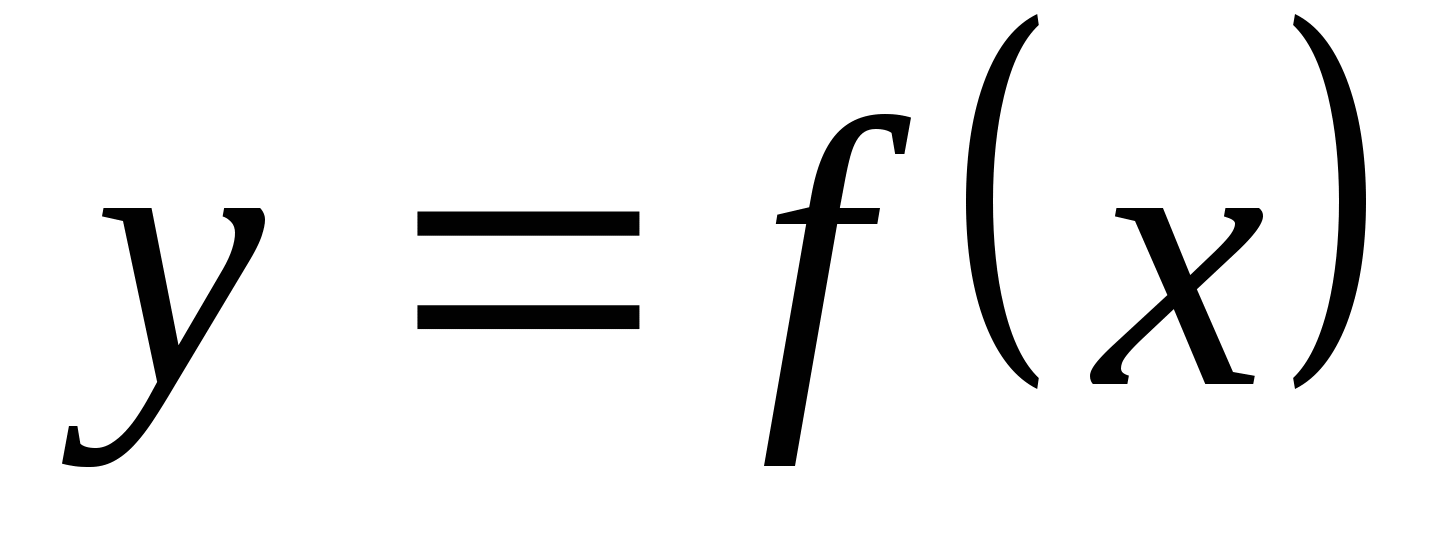 убывает на R. Решите неравенство
убывает на R. Решите неравенство
![]() .
.
______________________________________________________________
6. Найдите функцию, обратную функции ![]() . Постройте
. Постройте
на одном чертеже графики указанных двух взаимно обратных функций.
_______________________________________
7. Вычислите: ![]() .
.
Контрольная работа № 3 (1 час)
Вариант 1
-
Центр окружности единичного радиуса совпадает с началом координат плоскости хОу. Принадлежат ли дуге
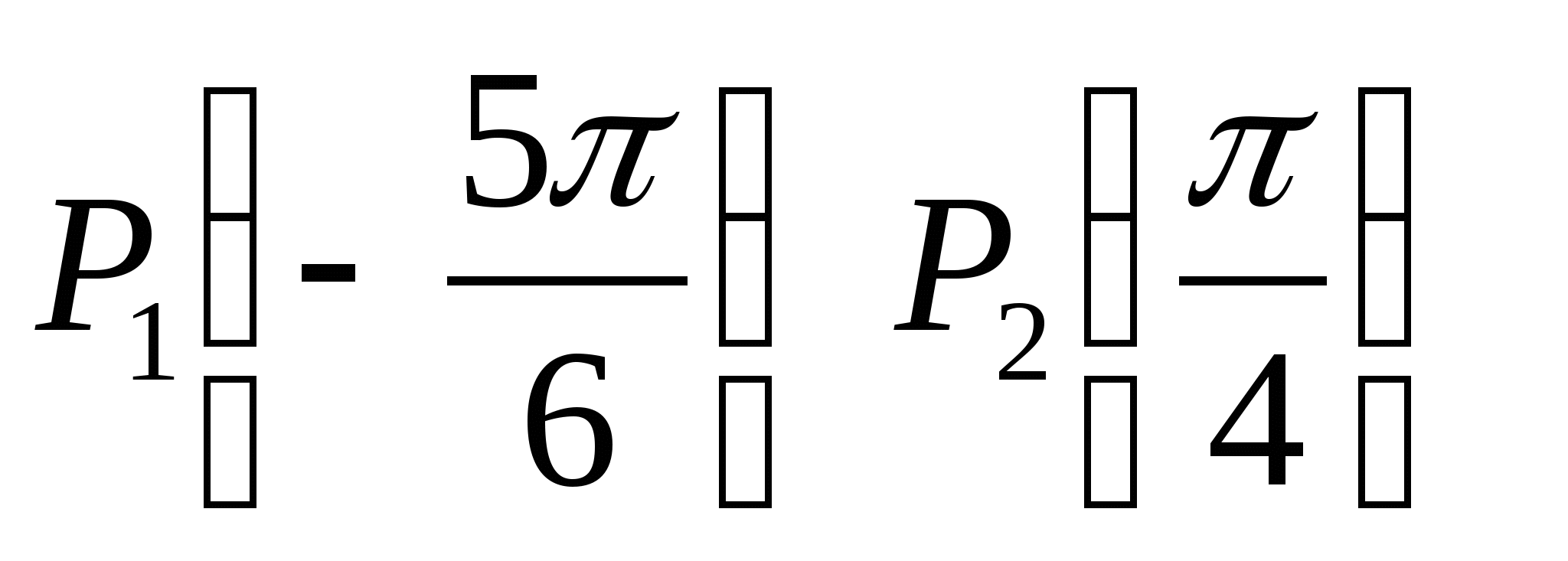 точки М1(-1; 0),
М2 (0; -1), М3
точки М1(-1; 0),
М2 (0; -1), М3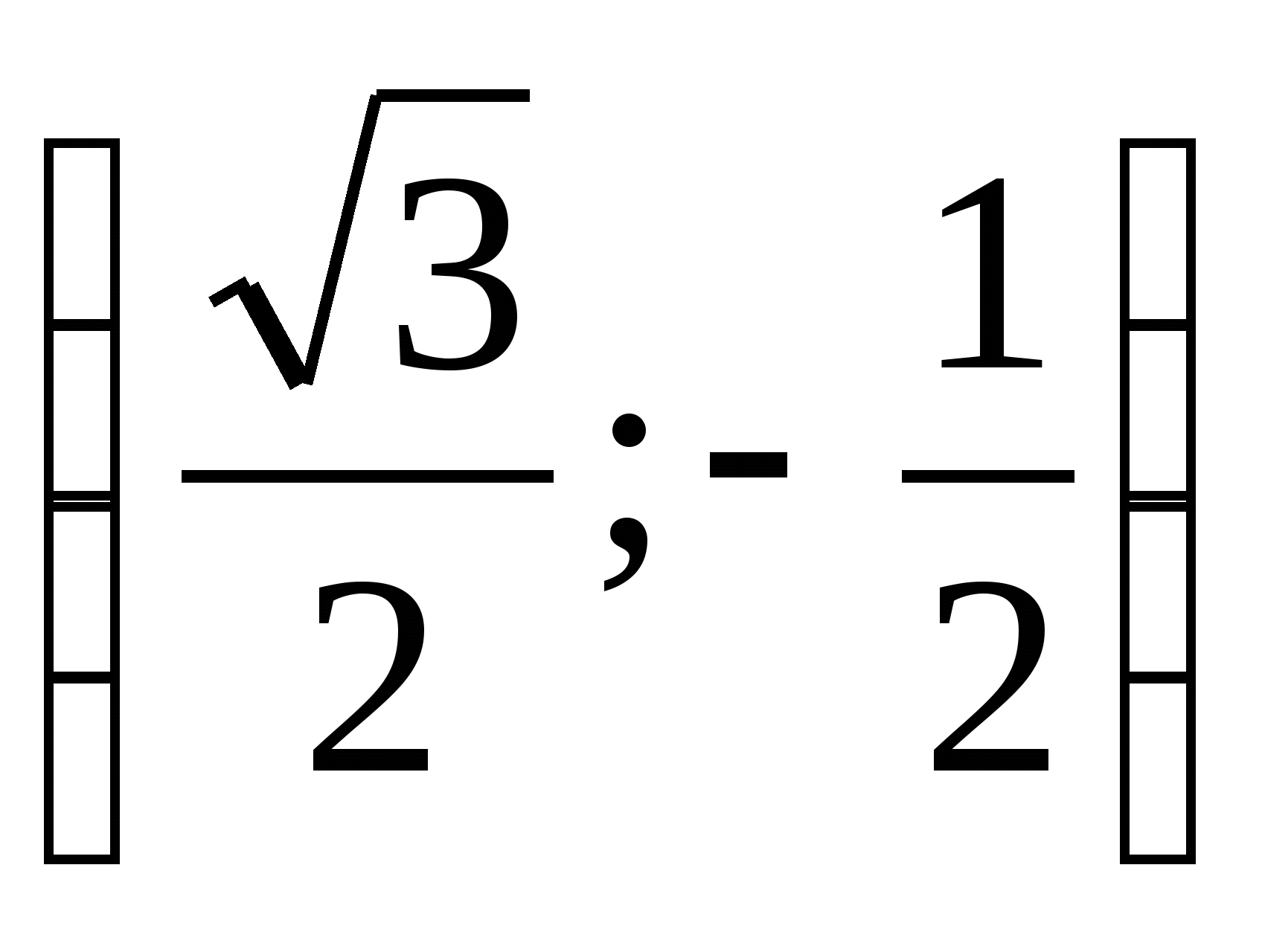 , М4
, М4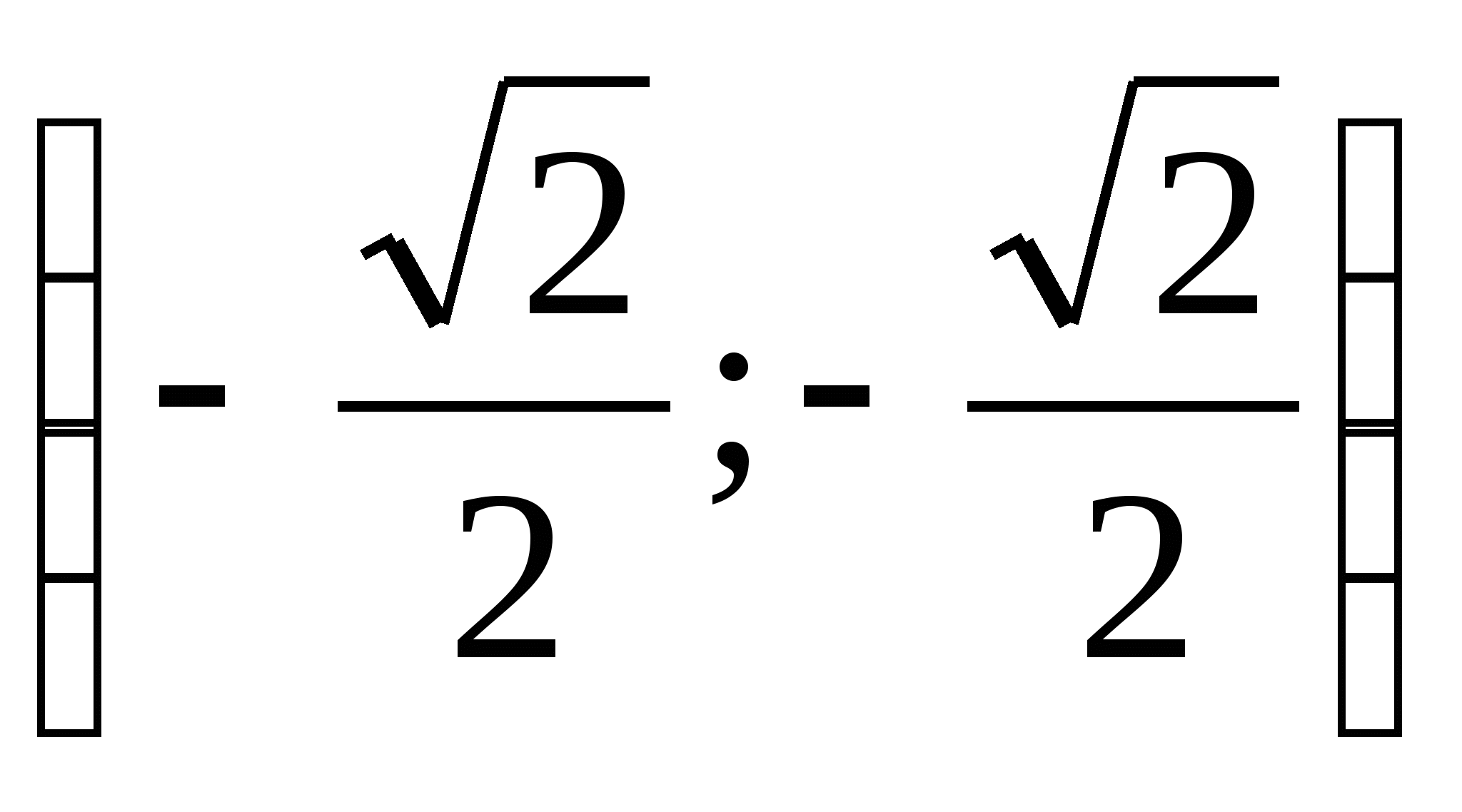 ?
?
-
Вычислите:
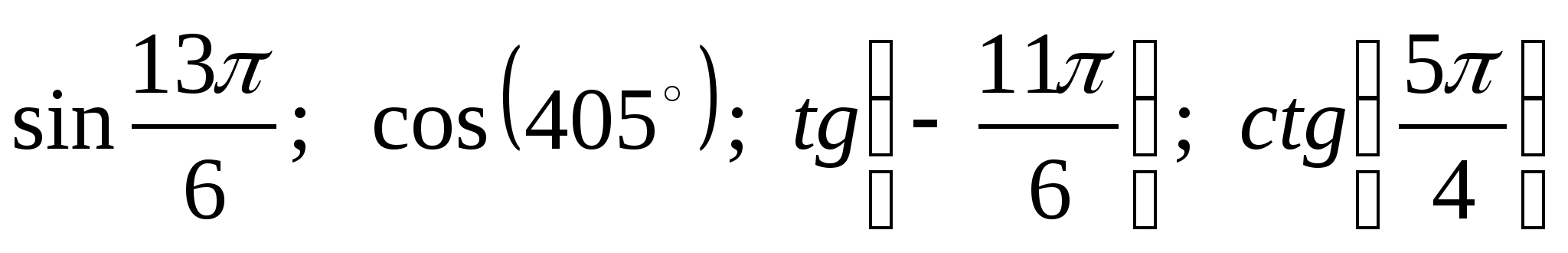 .
.
-
Вычислите
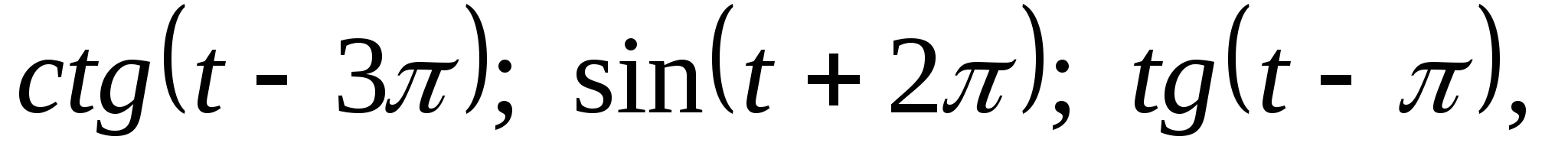 если
если 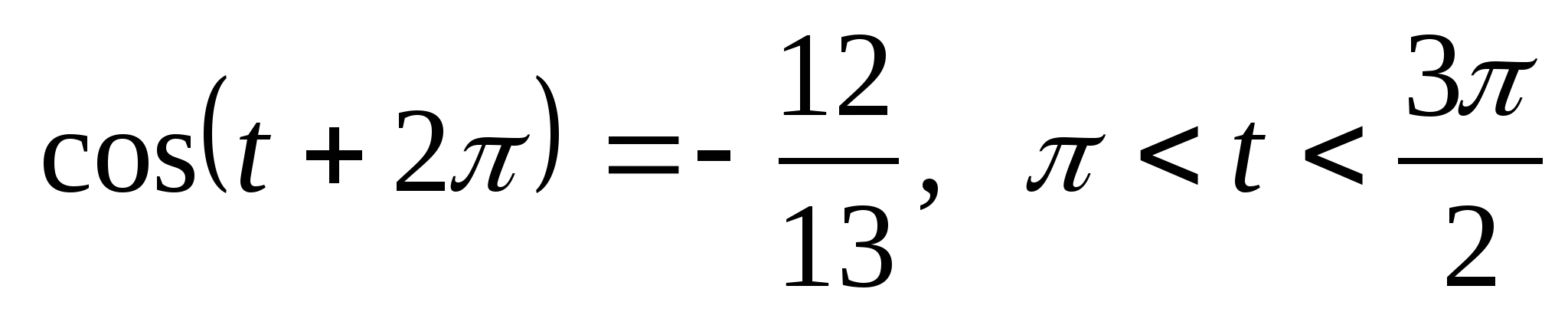 .
.
-
Решите неравенство: а)
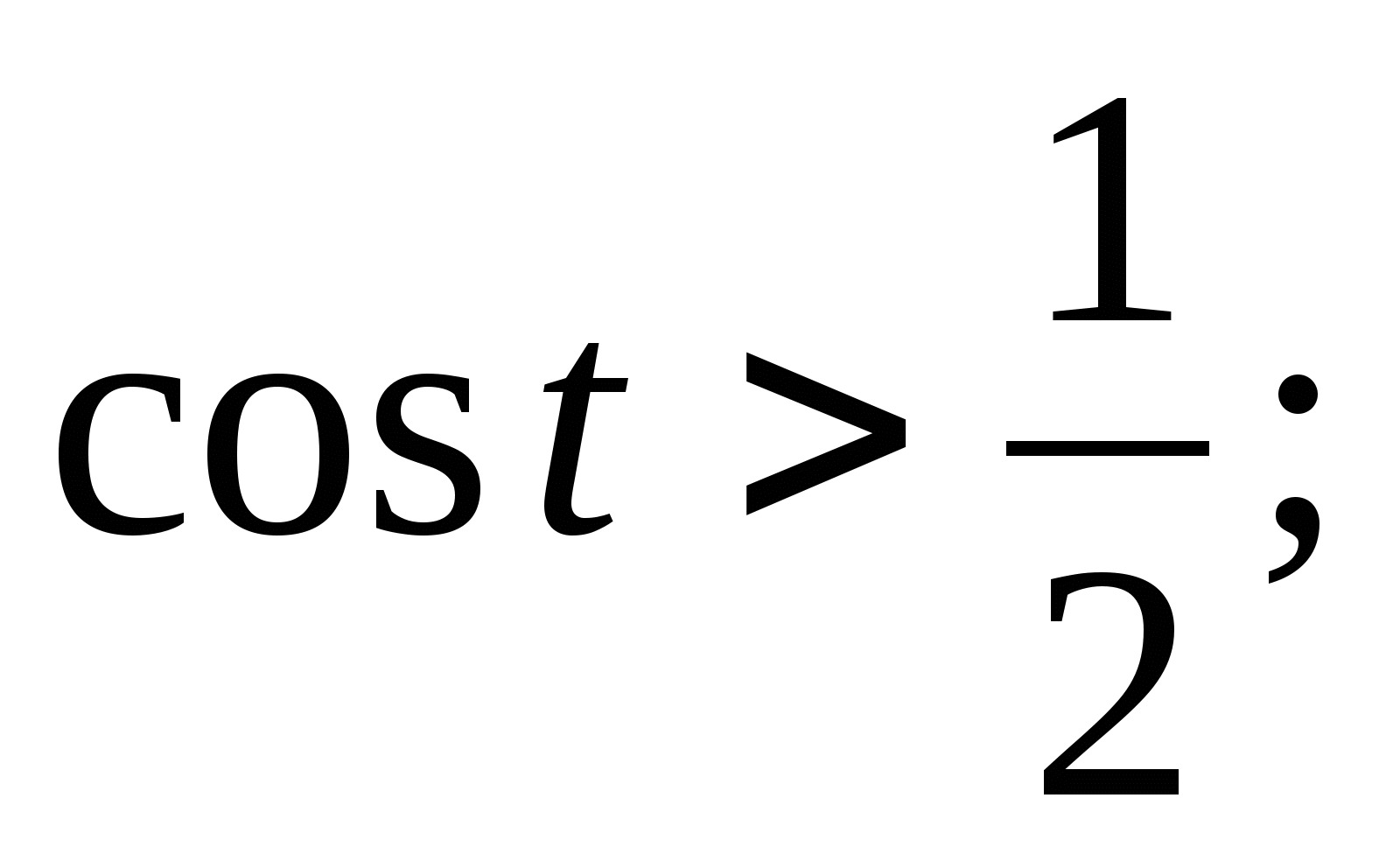 б)
б)
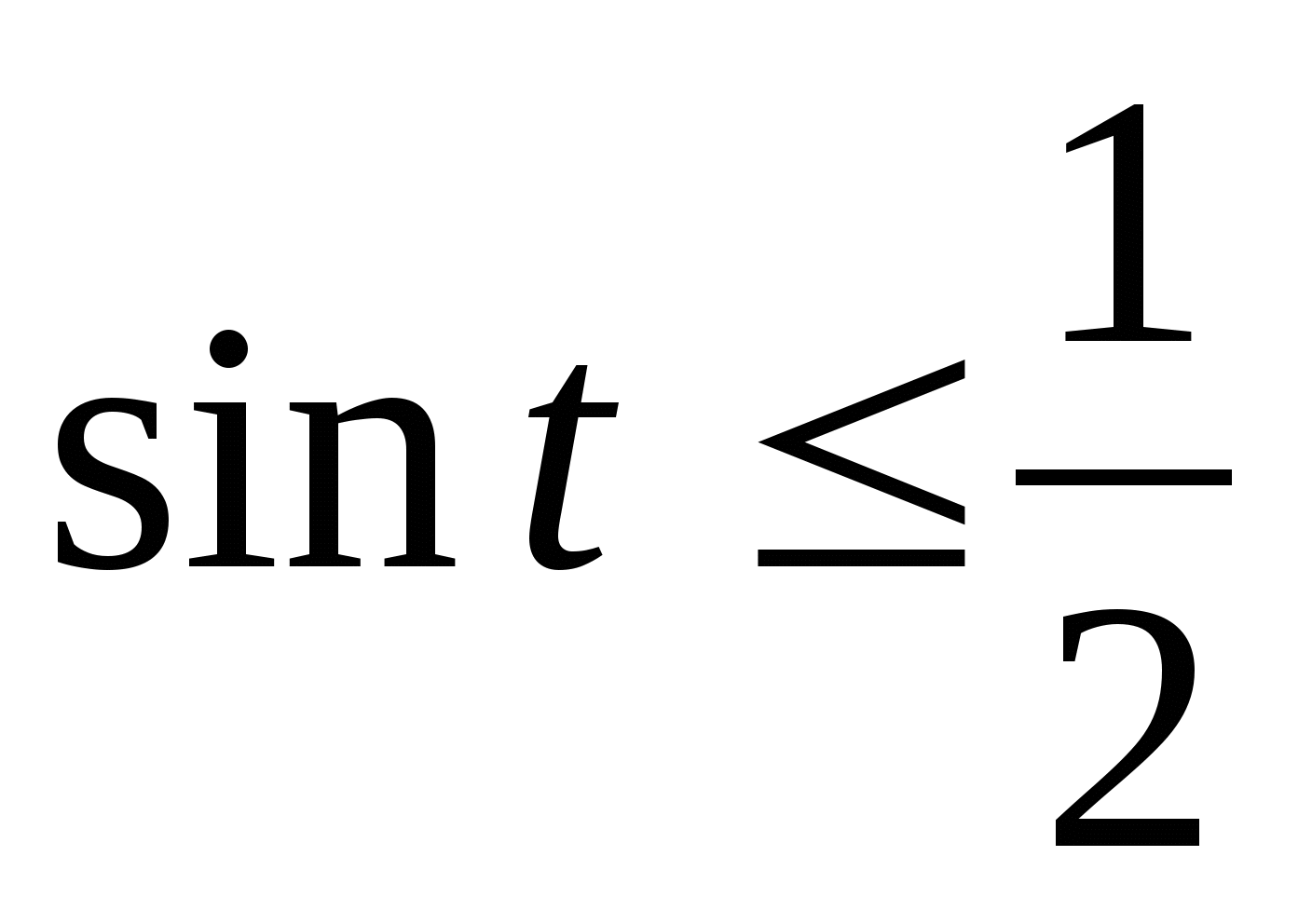 .
.
-
Постройте график функции
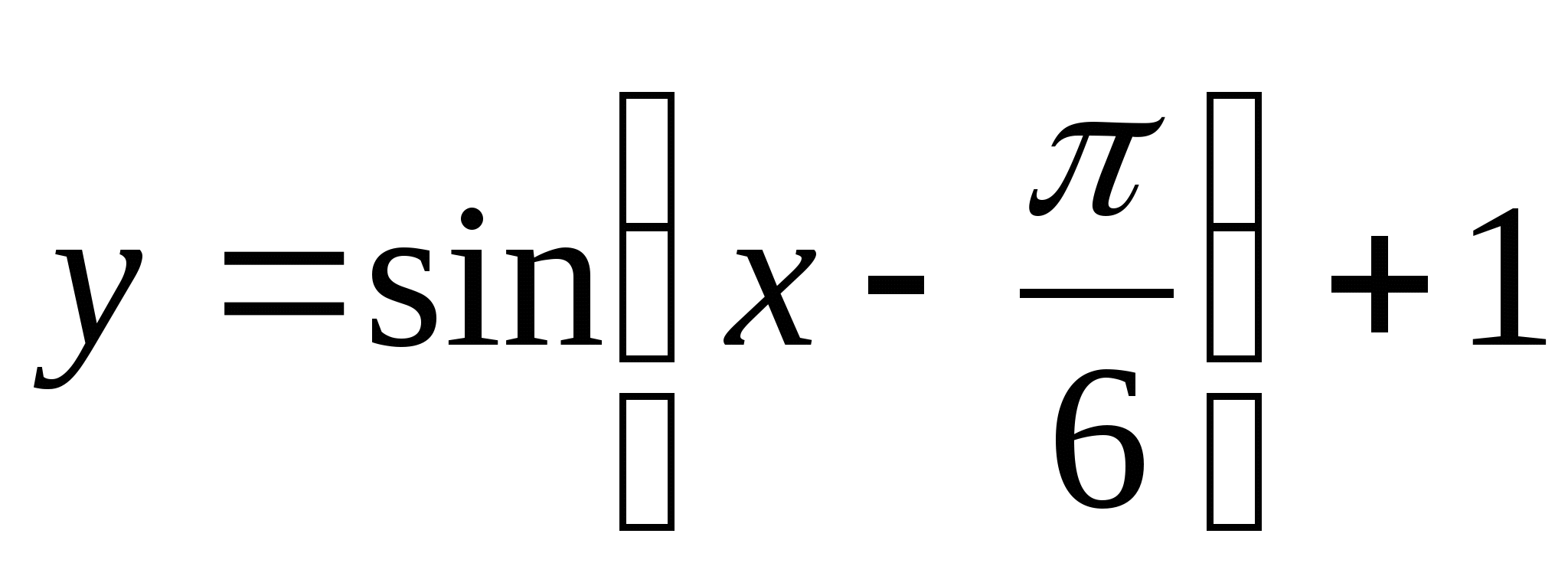 .
.
-
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
![]()
___________________________________________________________________
7. Сравните числа ![]() .
.
______________________________________
8. Решите неравенство ![]() .
.
Вариант 2
-
Центр окружности единичного радиуса совпадает с началом координат плоскости хОу. Принадлежат ли дуге
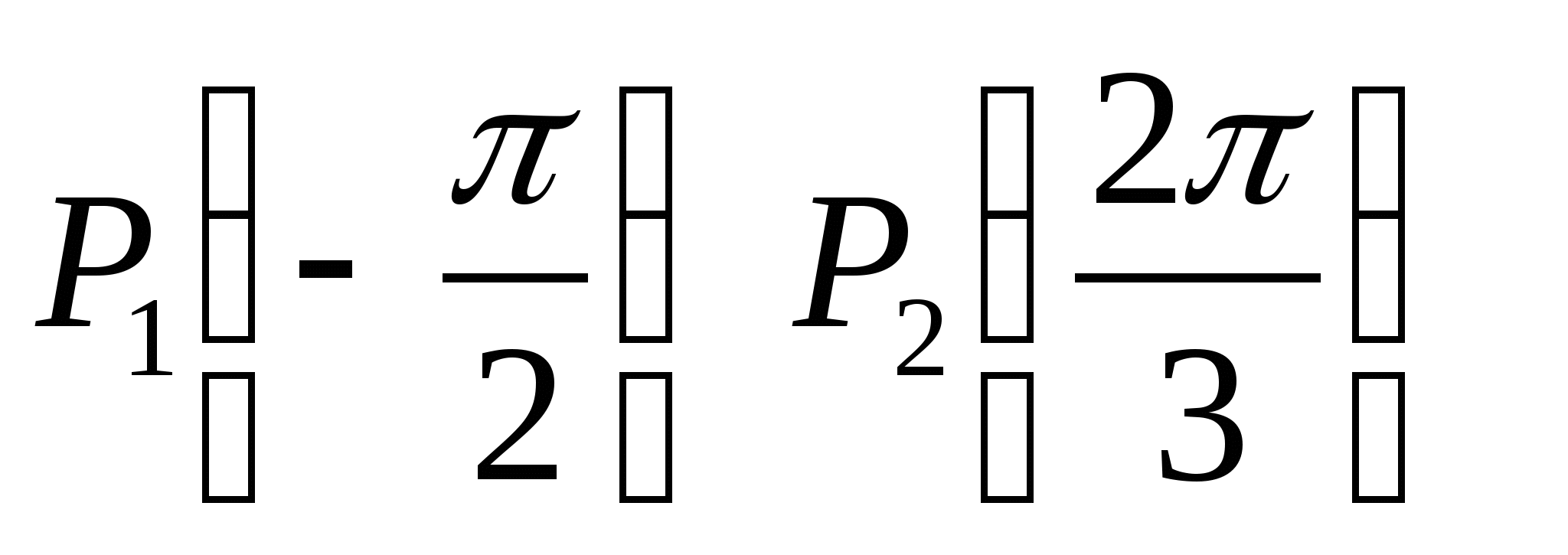 точки М1
точки М1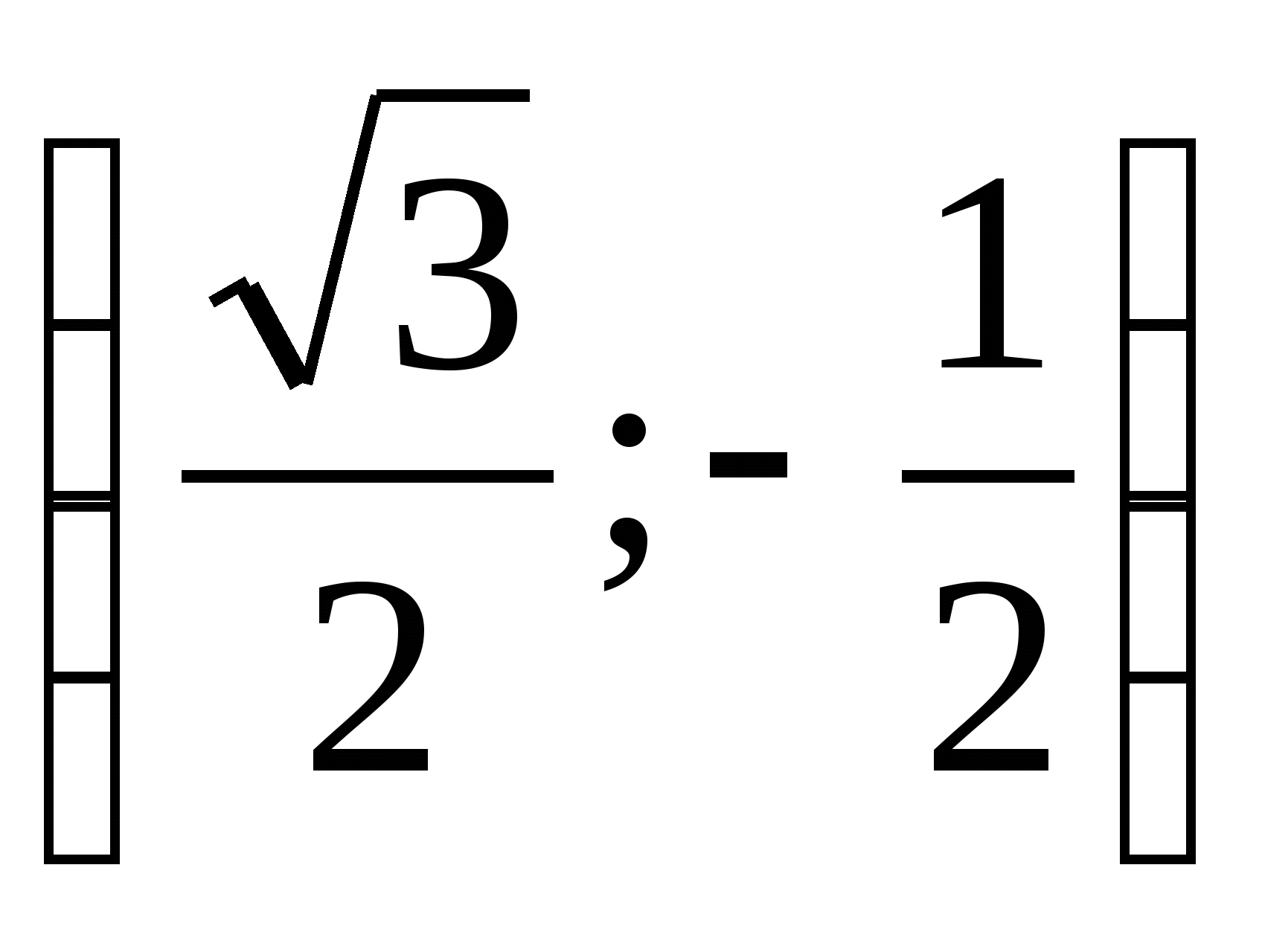 , М2 (0; 1),
М3
, М2 (0; 1),
М3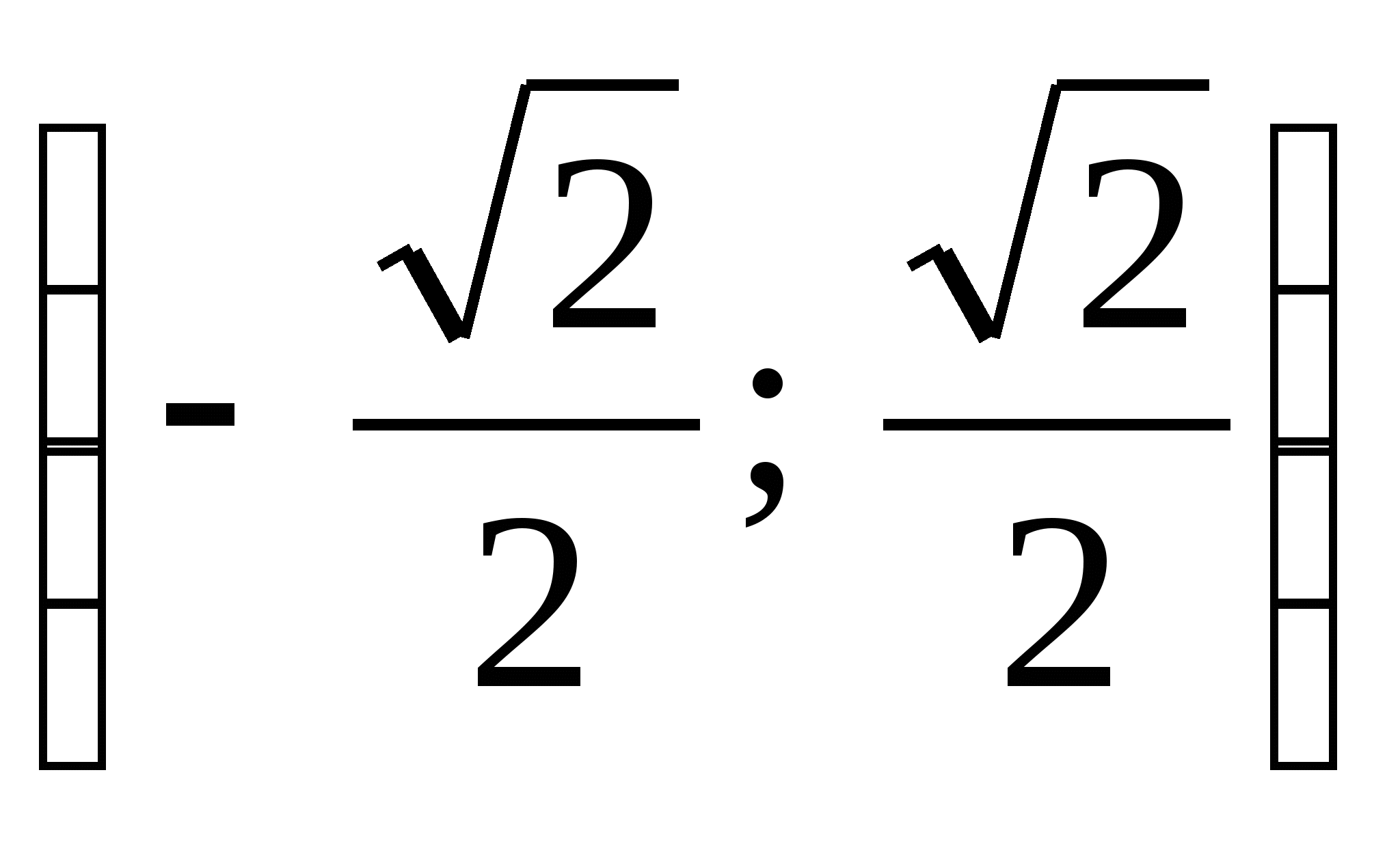 ,
М4
,
М4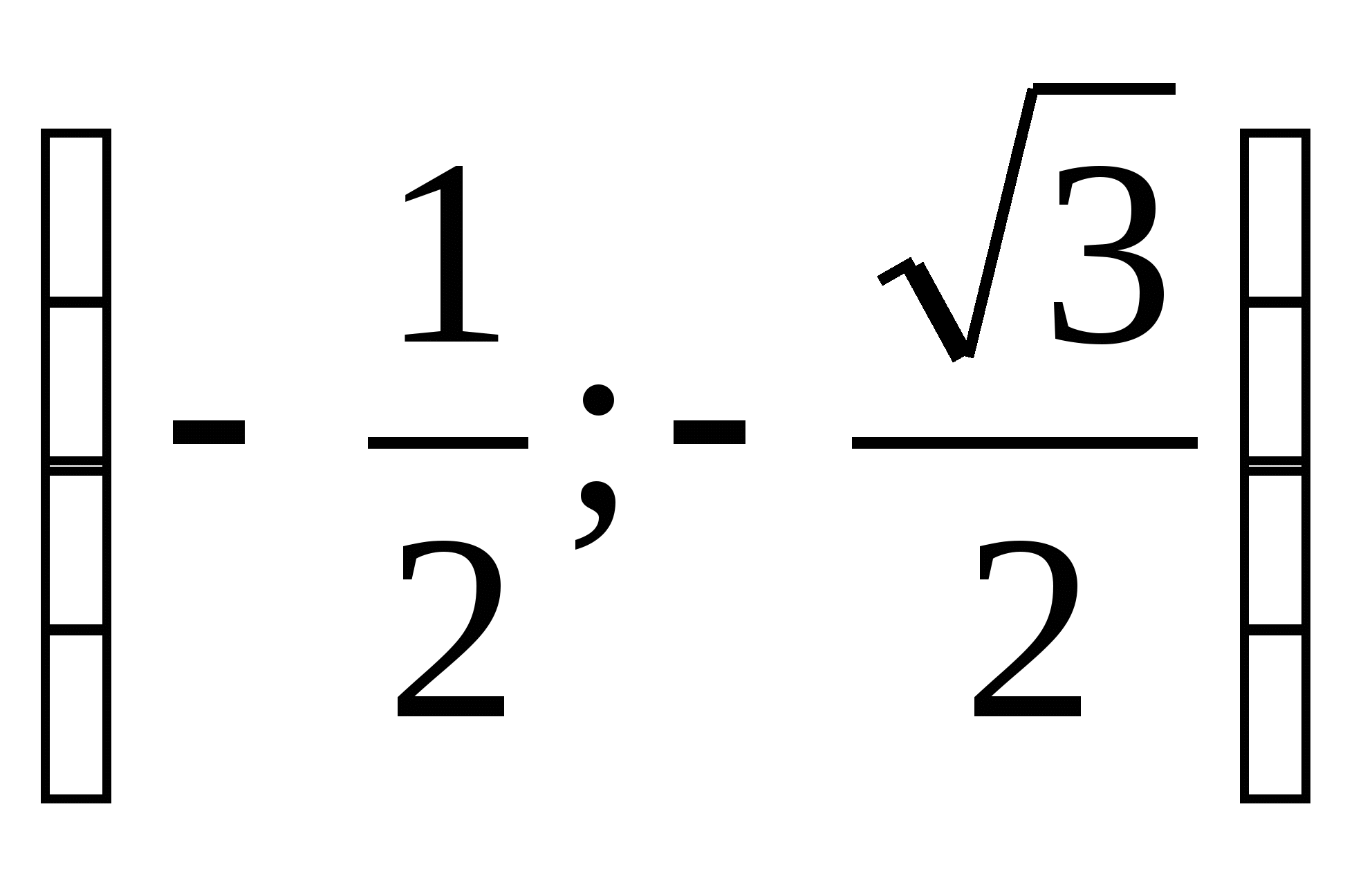 ?
?
-
Вычислите:
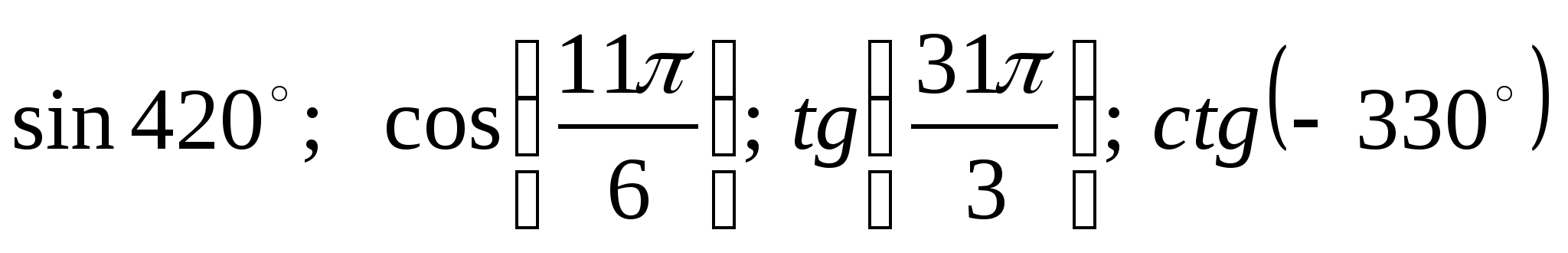 .
.
-
Вычислите
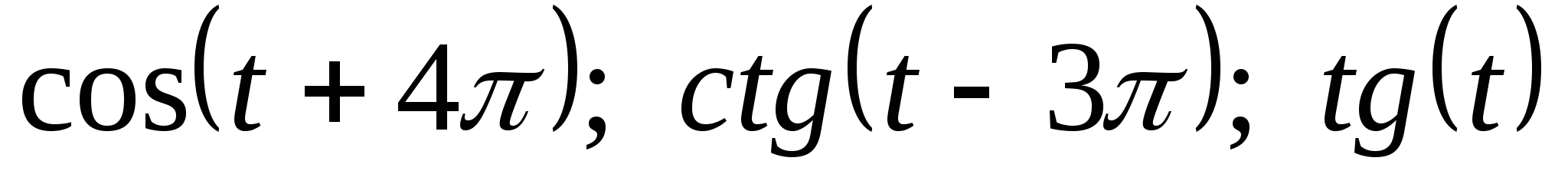 , если
, если 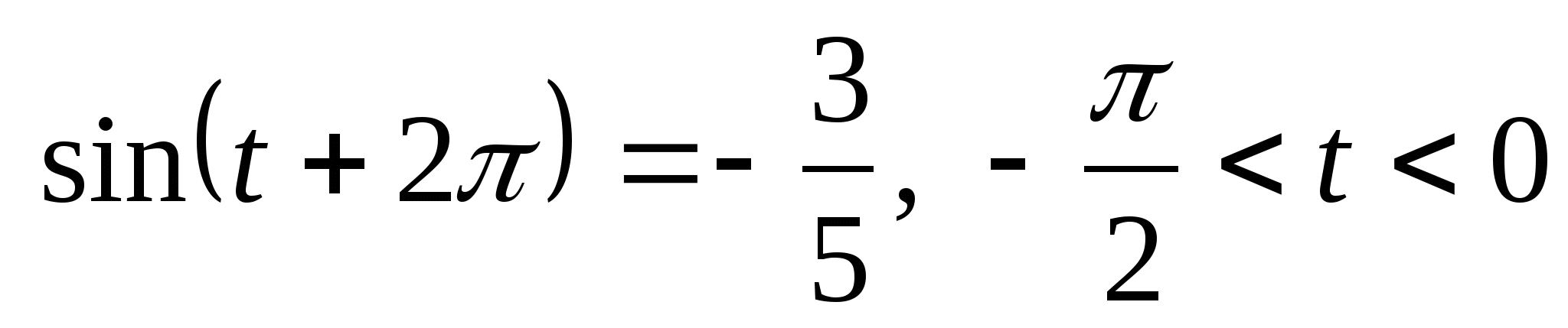 .
.
-
Решите неравенство: а)
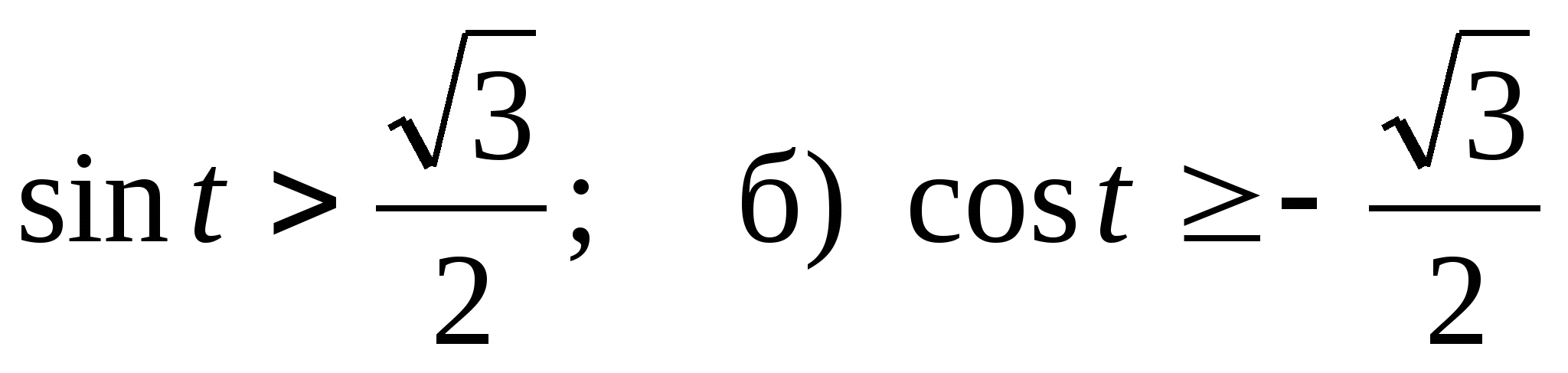
-
Постройте график функции
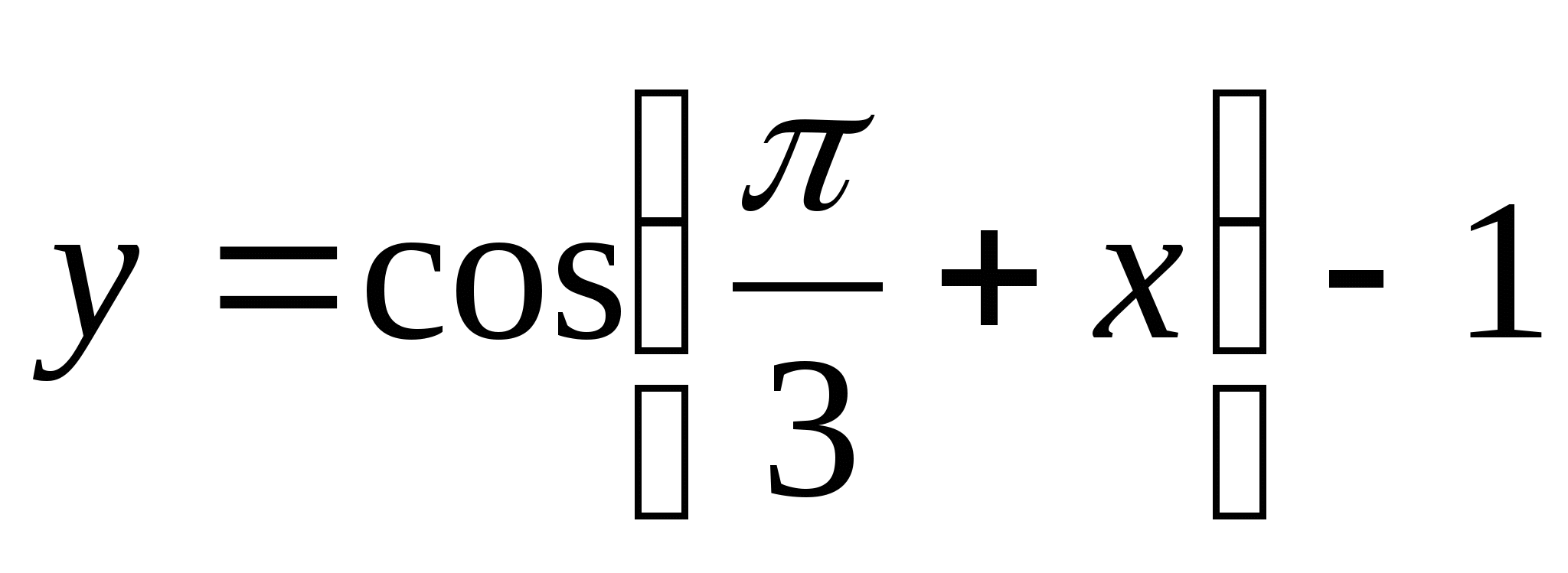 .
.
-
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
![]()
____________________________________________________________
7. Сравните числа ![]() .
.
_______________________________________
8. Решите неравенство ![]() .
.
Контрольная работа № 4 (2 часа)
Вариант 1
-
Вычислите:
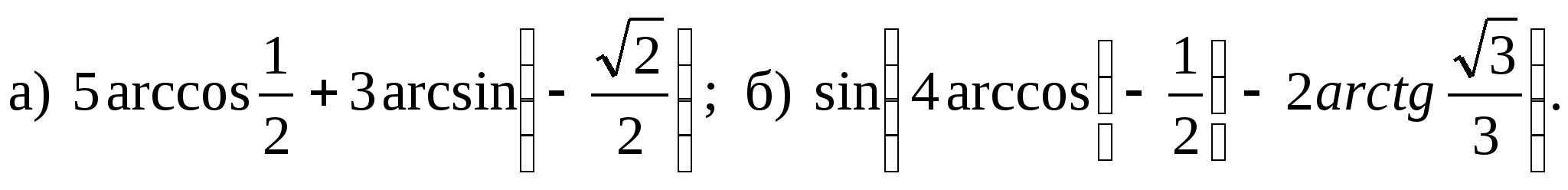
-
Постройте график функции
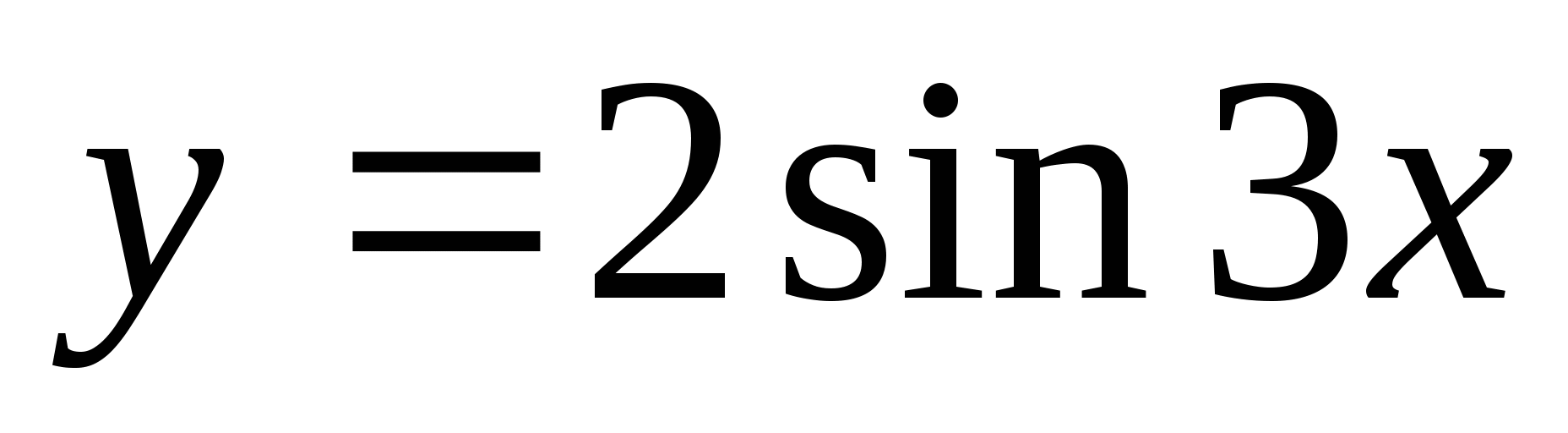 .
.
-
Решите уравнение: а)
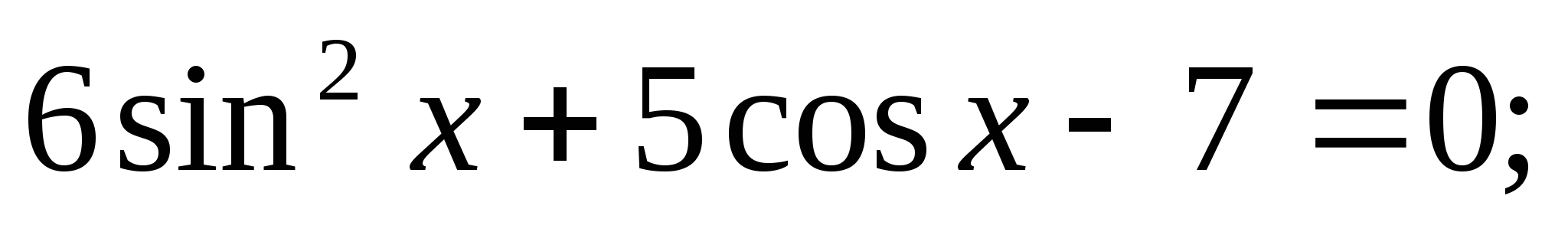
б) ![]() .
.
-
Найдите корни уравнения
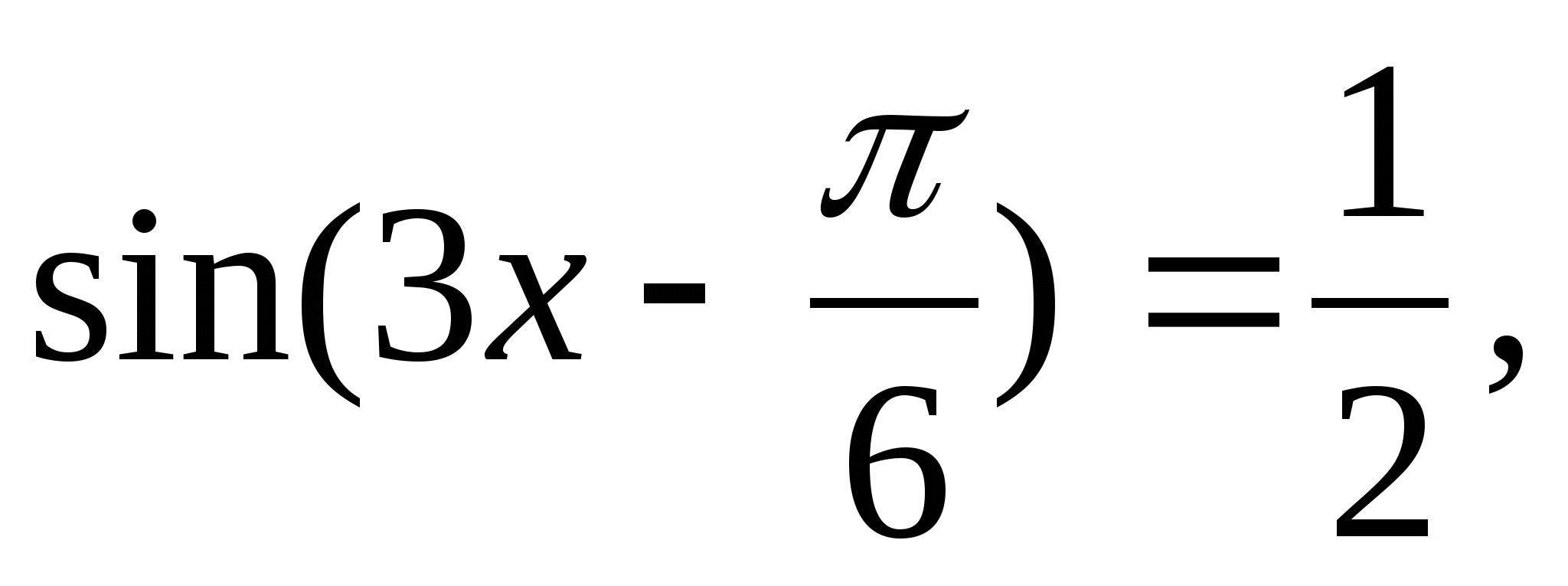 принадлежащие промежутку
принадлежащие промежутку 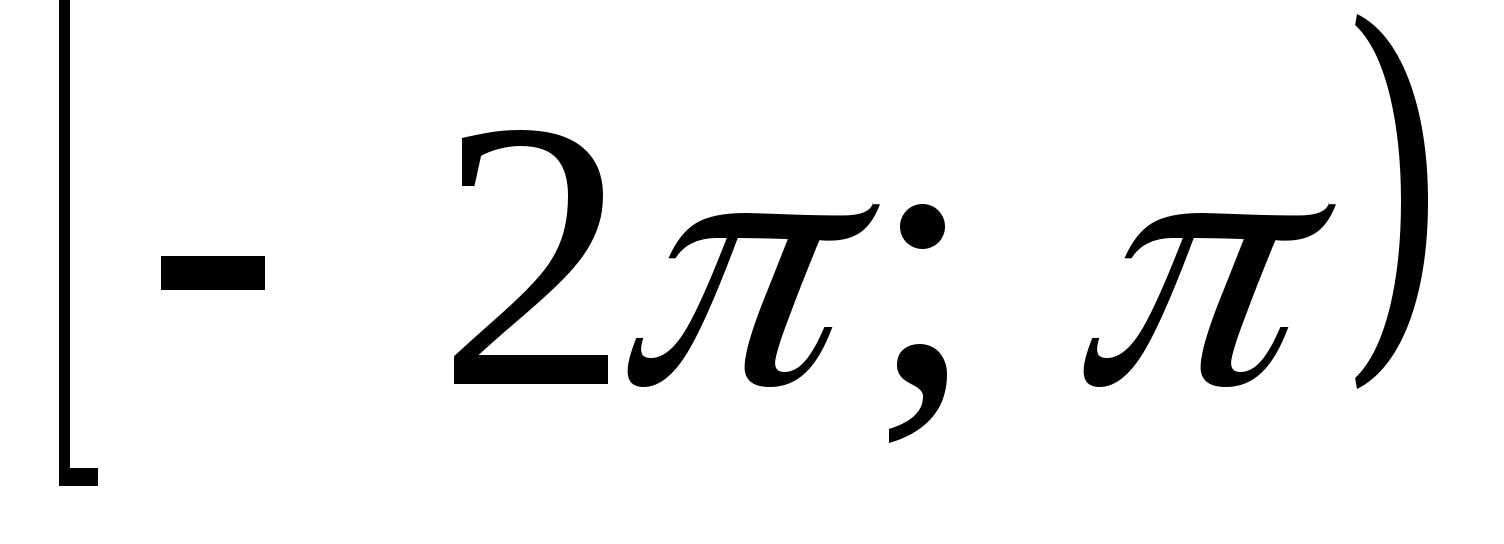 .
.
-
Постройте график функции
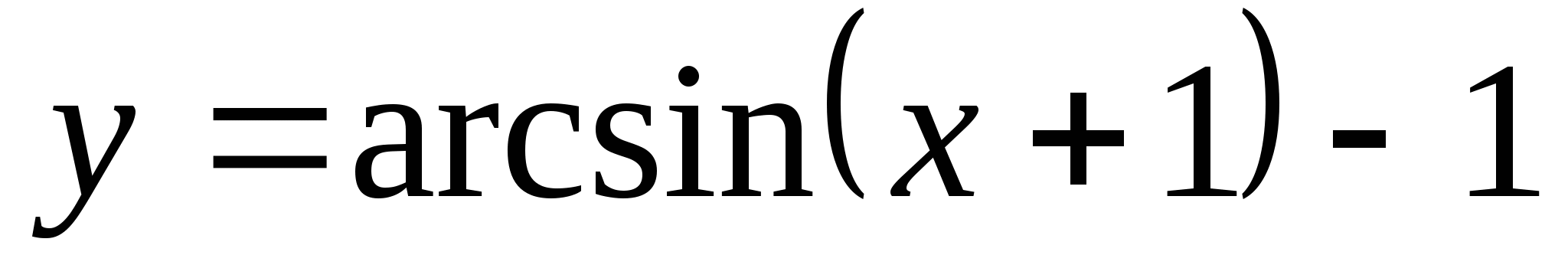 .
.
____________________________________________________________
6. Решите систему неравенств: а) 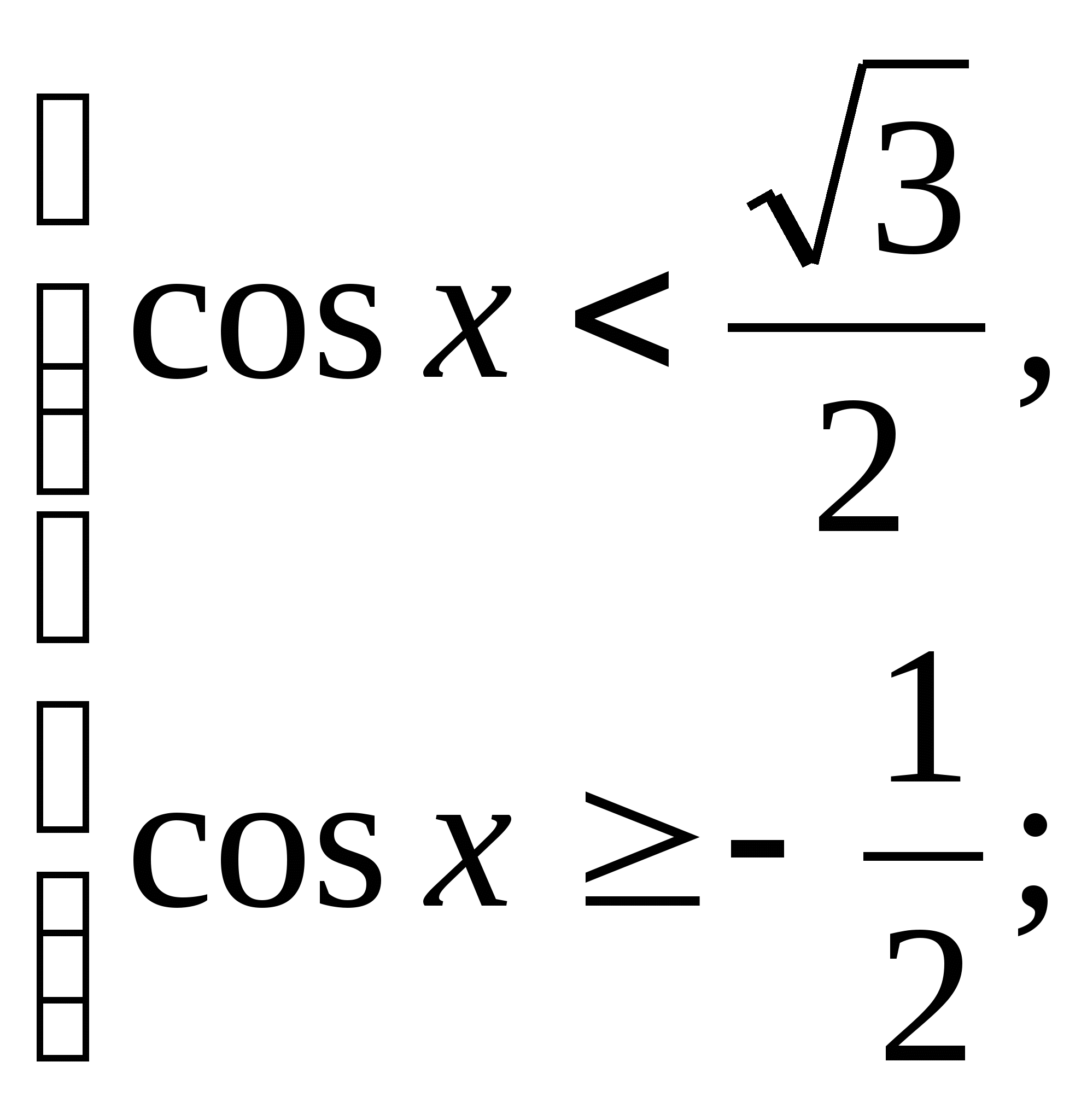 б)
б) 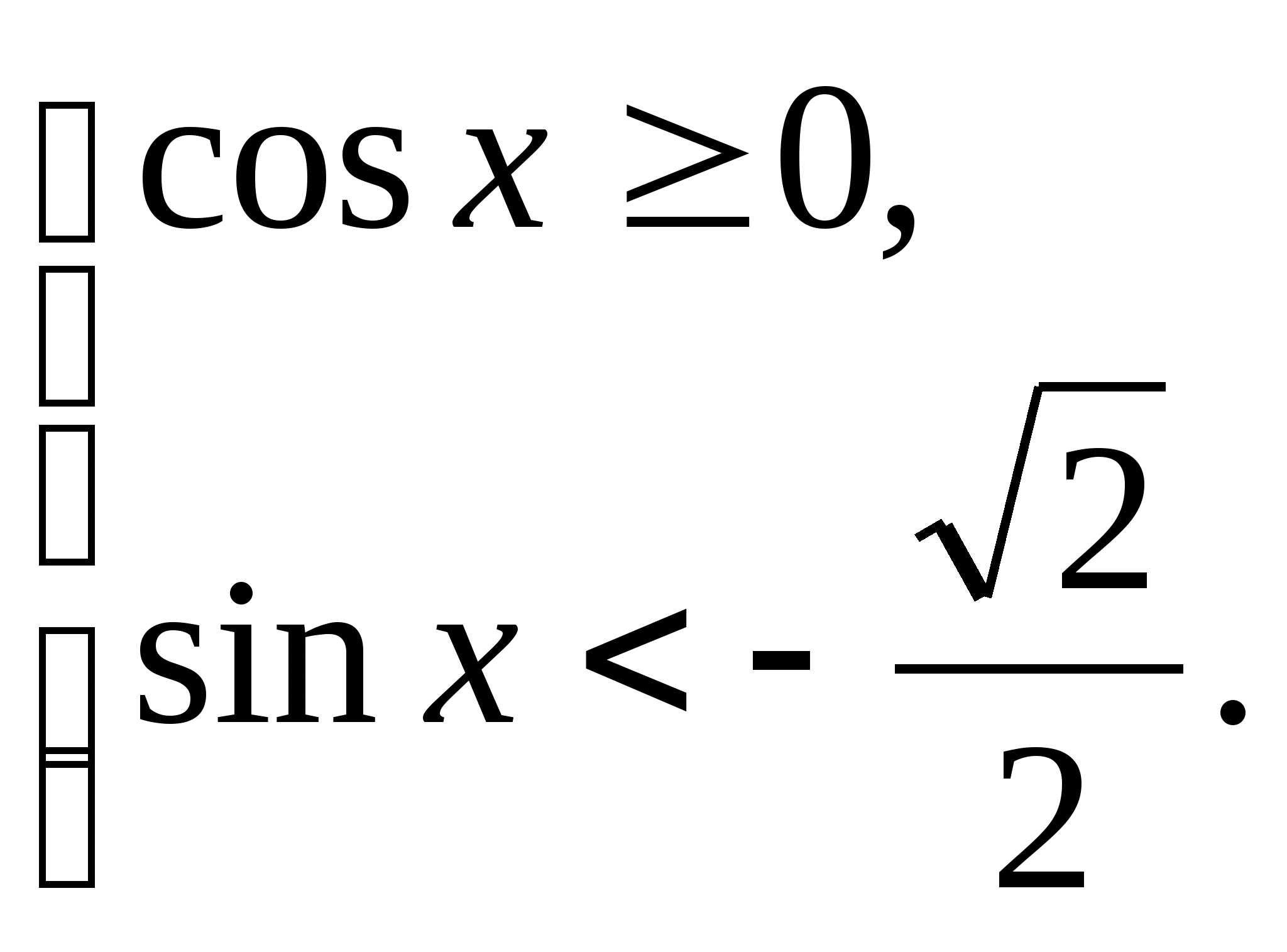
___________________________________
7. Решите уравнение ![]() .
.
Вариант 2
1. Вычислите: ![]()
2. Постройте график функции ![]() .
.
3. Решите уравнение: а) ![]()
б) ![]() .
.
4. Найдите корни уравнения![]() принадлежащие промежутку
принадлежащие промежутку ![]() .
. ![]()
5. Постройте график функции ![]() .
.
____________________________________________________________
6. Решите систему неравенств: а) 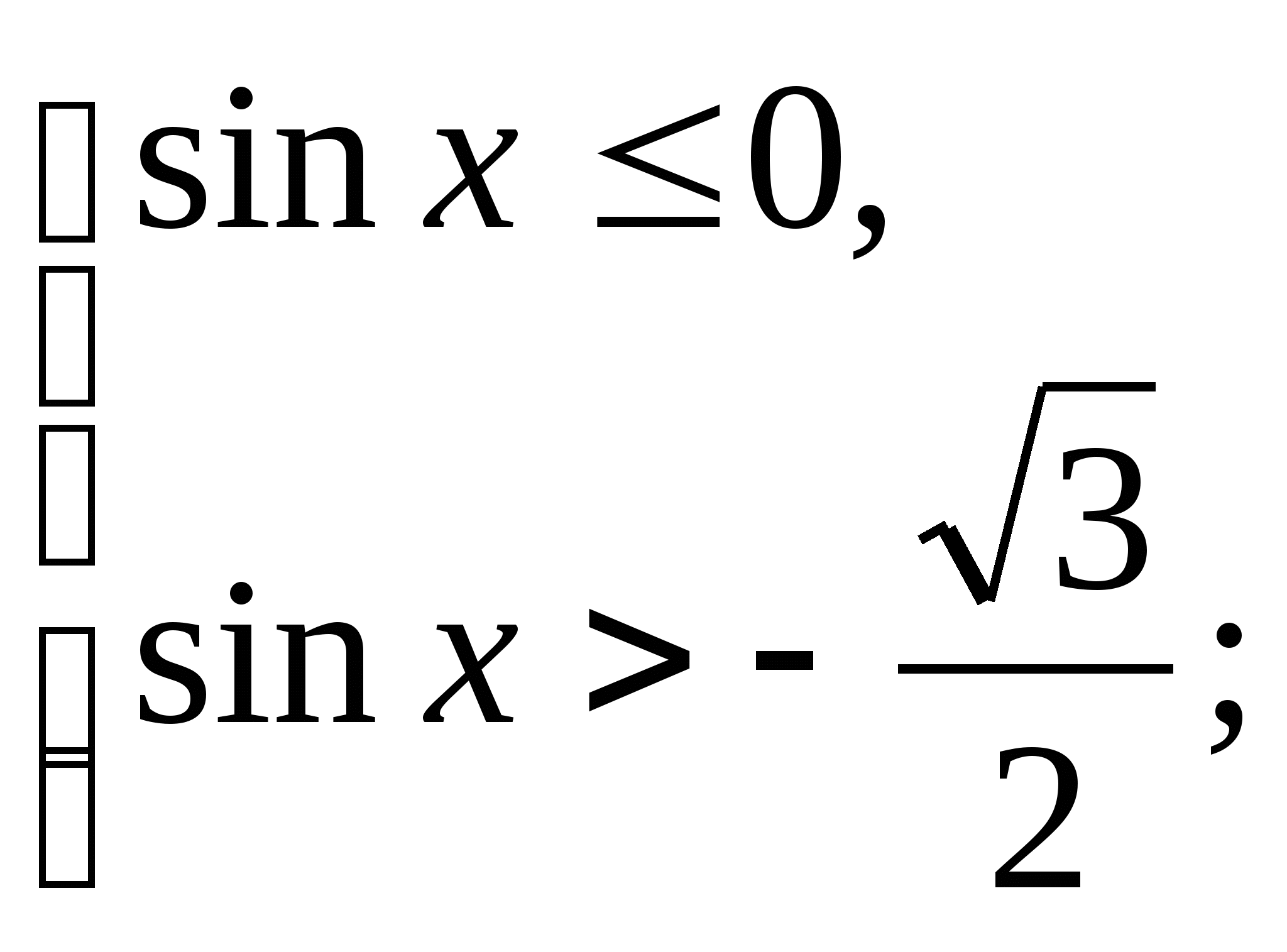 б)
б) 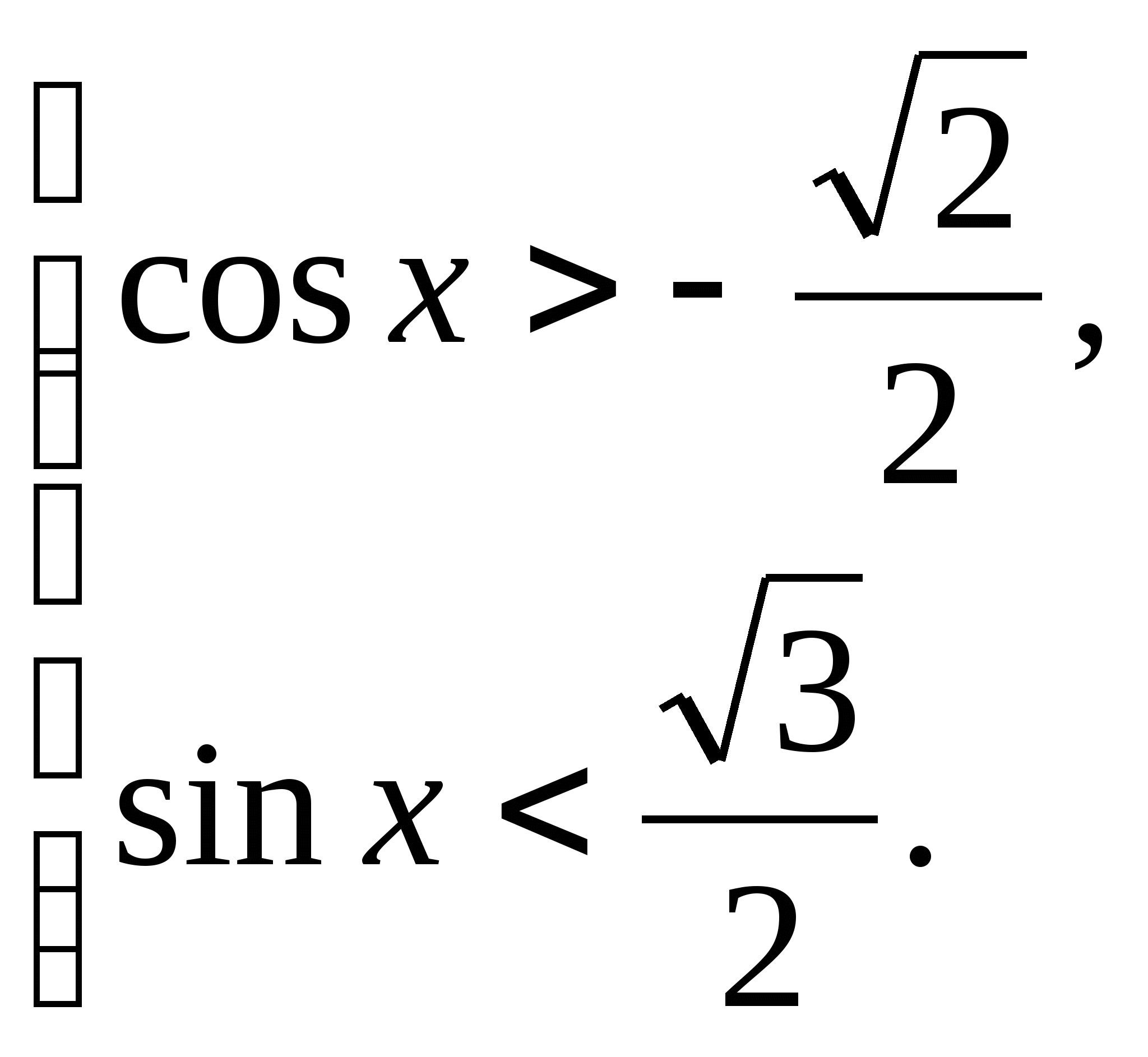
___________________________________
7. Решите уравнение ![]() .
.
Контрольная работа № 5 (2 часа)
Вариант 1
-
Докажите тождество:
а) ![]() ,
,
б) ![]() .
.
-
Упростите выражение
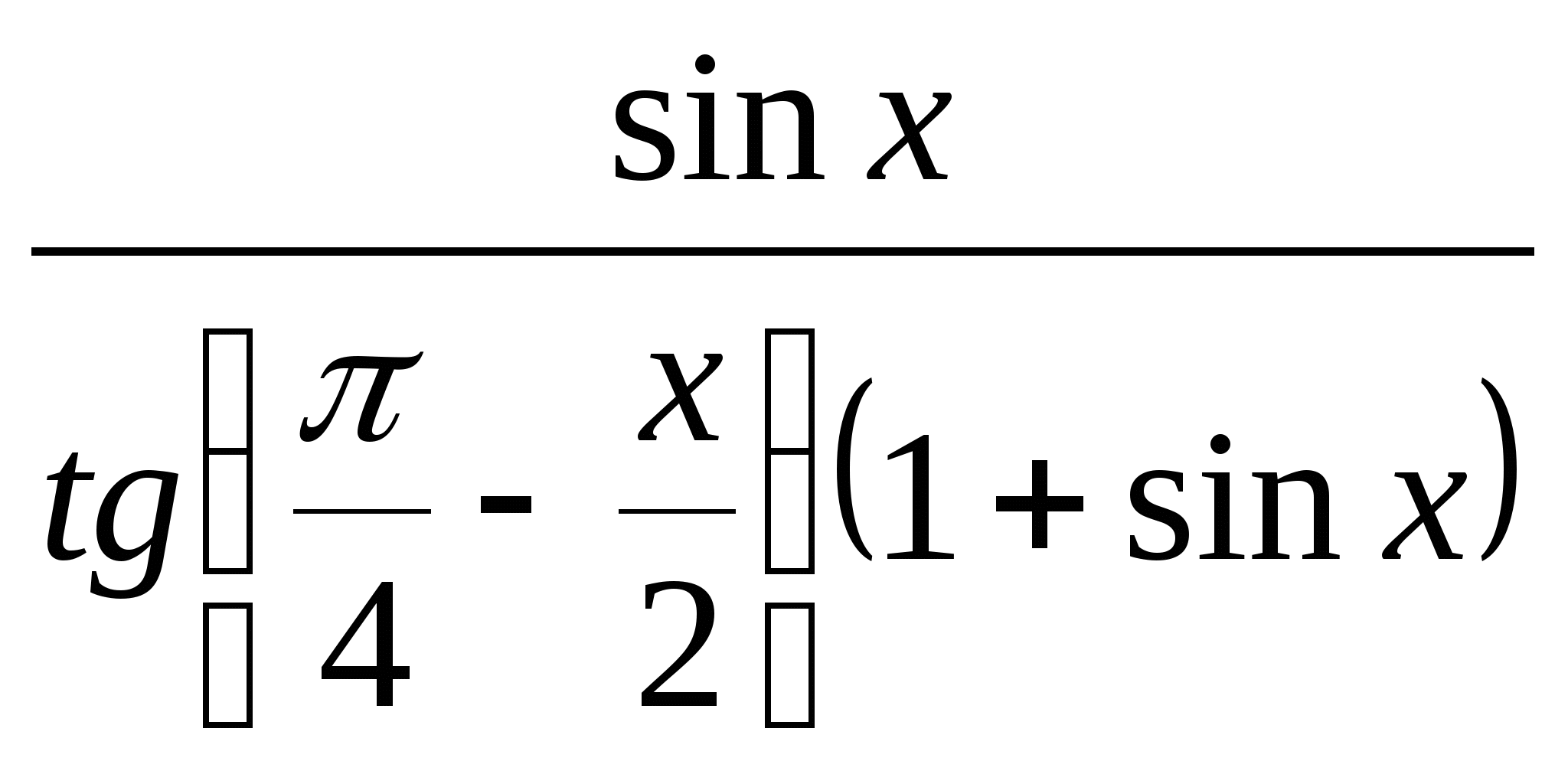 .
.
-
Вычислите
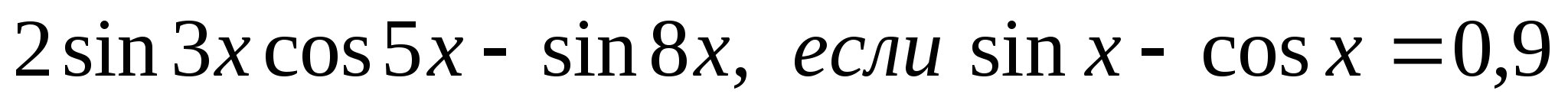 .
.
-
Найдите
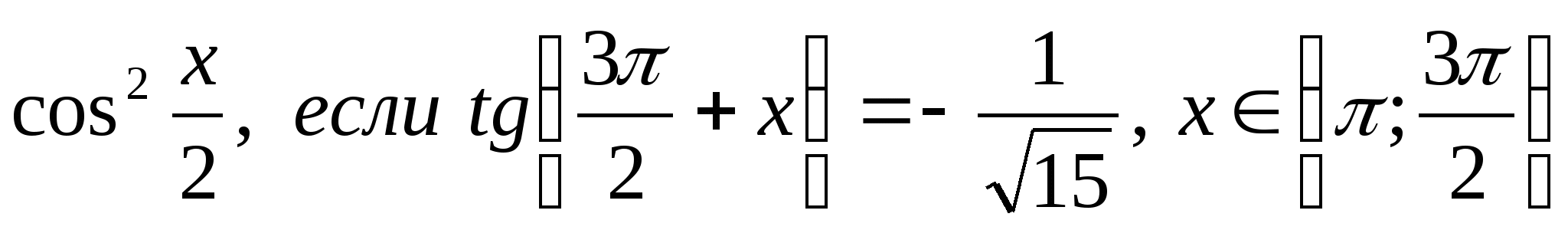 .
.
-
Найдите корни уравнения
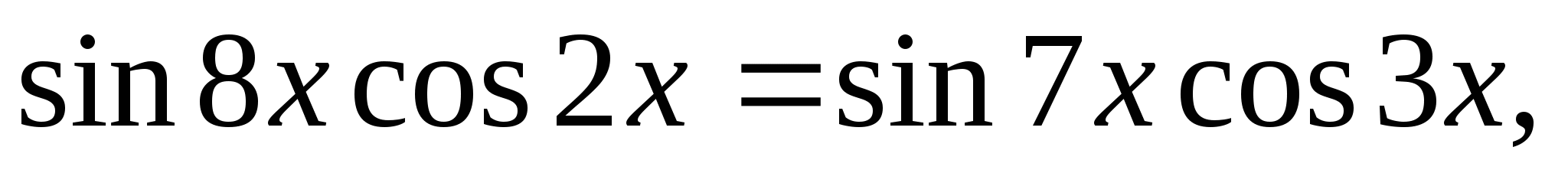 принадлежащие промежутку
принадлежащие промежутку  .
.
-
Решите уравнение: а)
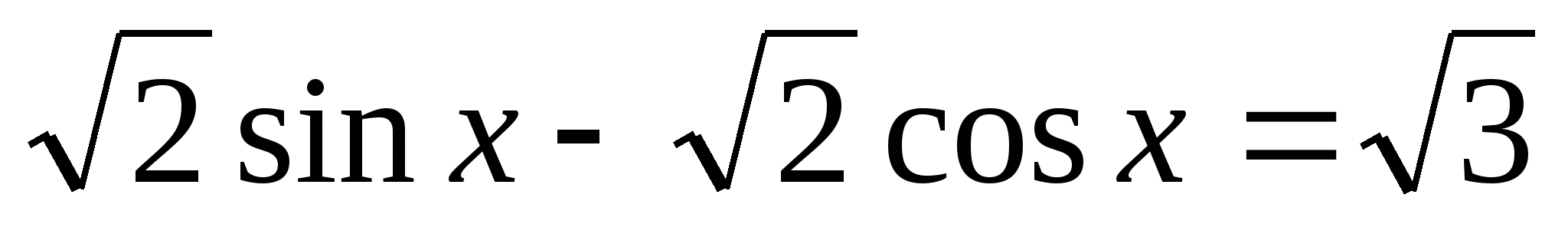 ;
;
б) ![]() .
.
____________________________________________________________
7. Вычислите ![]() .
.
____________________________________________________________
8. Решите уравнение ![]() .
.
Вариант 2
1. Докажите тождество:
а) ![]() ,
,
б) ![]() .
.
2. Упростите выражение 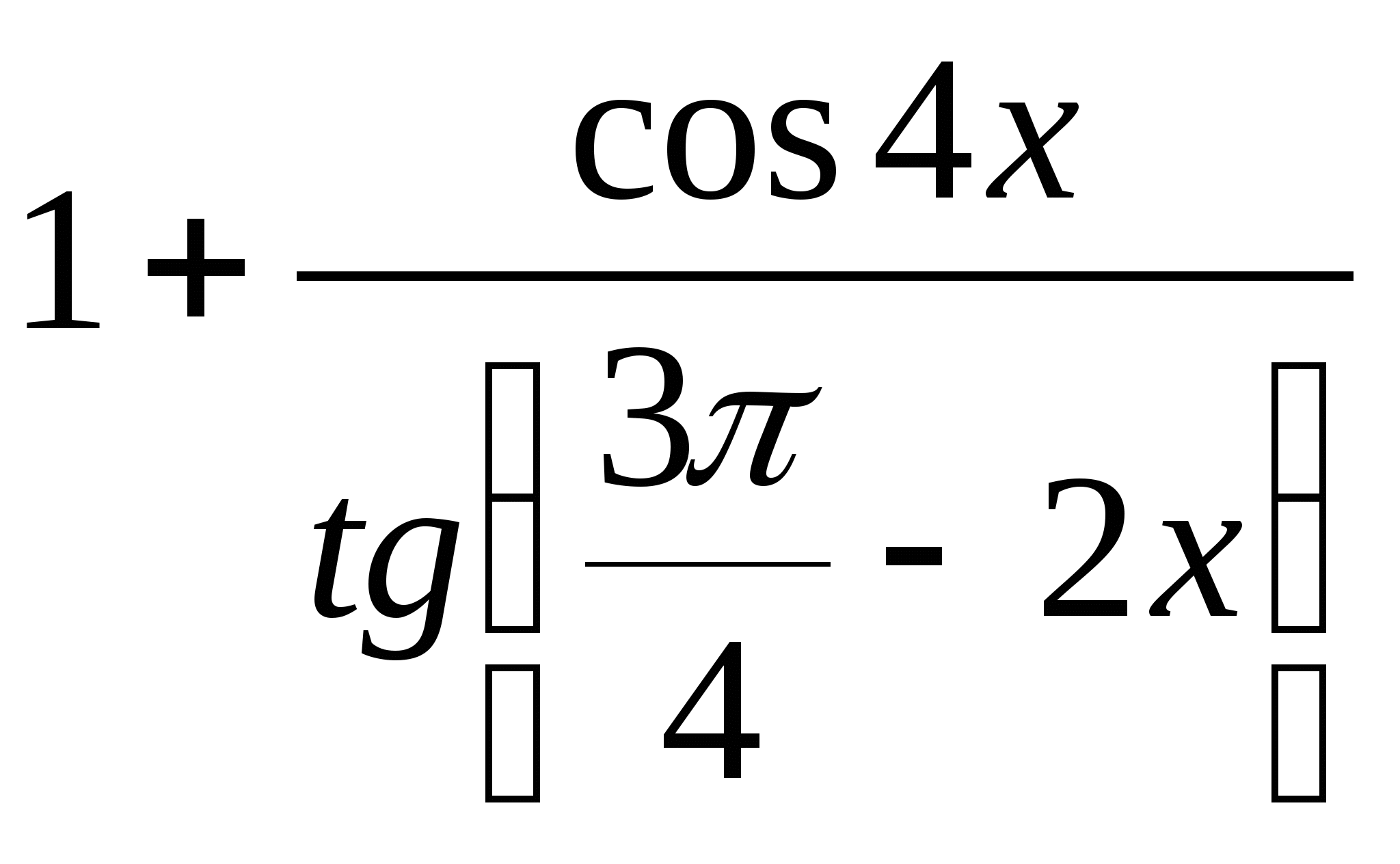 .
.
3. Вычислите ![]() .
.
4. Найдите ![]() .
.
5. Найдите корни уравнения ![]()
принадлежащие промежутку ![]() .
.
6. Решите уравнение: а) ![]() ;
;
б) ![]() .
.
____________________________________________________________
7. Вычислите ![]() .
.
______________________________________________________
8. Решите уравнение ![]() .
.
Контрольная работа № 6 (1 час)
Вариант 1
-
Вычислите:
а)![]() , б)
, б)![]() .
.
-
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки ![]() ;
;
б) множество точек z, удовлетворяющих условию ![]() в) множество точек z,
удовлетворяющих условию
в) множество точек z,
удовлетворяющих условию ![]() .
.
-
Запишите комплексное число в стандартной тригонометри- ческой форме: а)
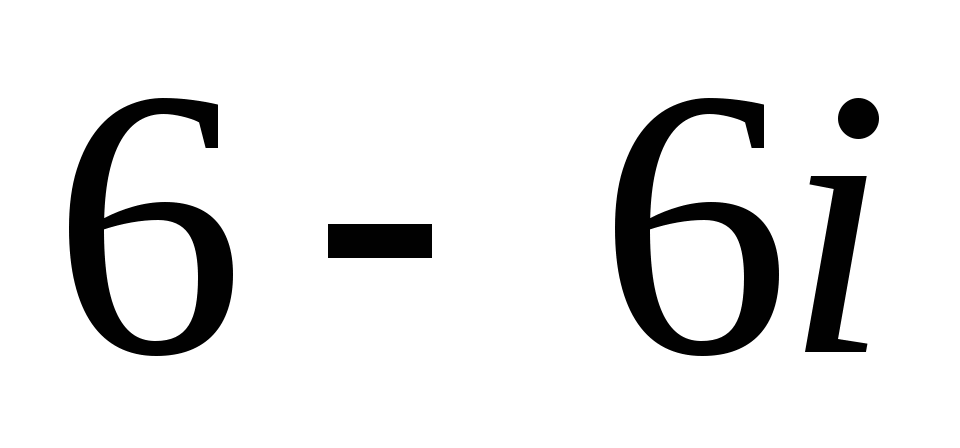 , б)
, б)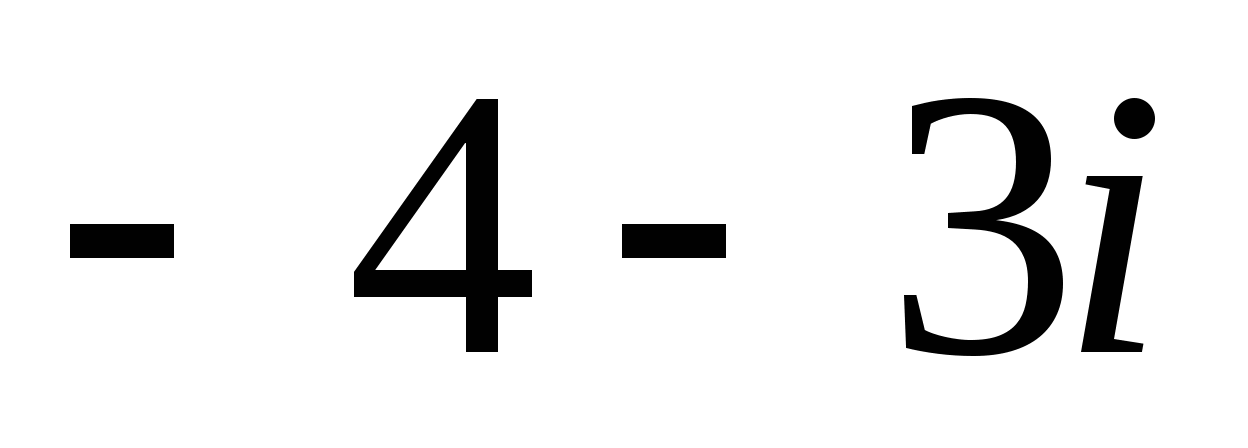 .
.
-
Решите уравнение
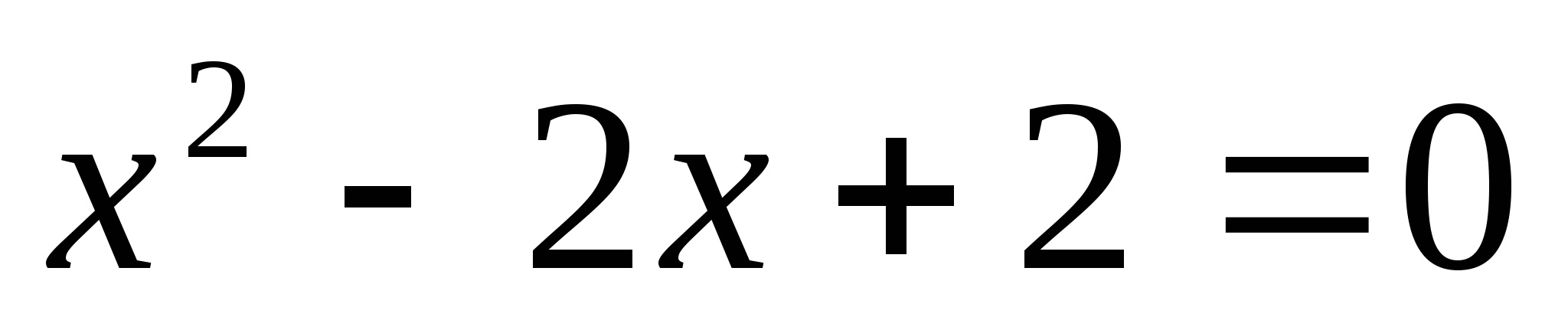 .
.
-
Вычислите
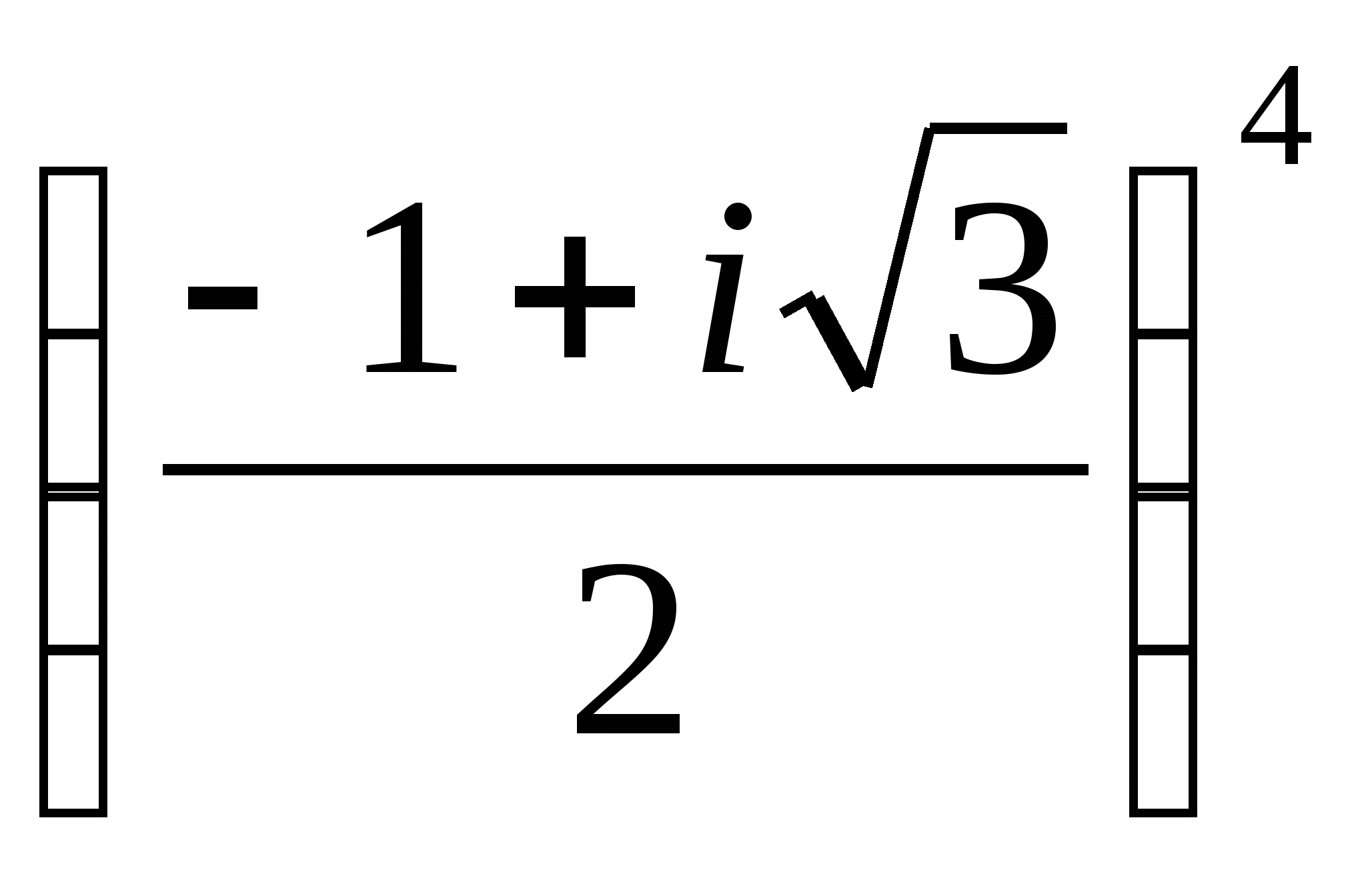 .
.
____________________________________________________________
6. Решите уравнение ![]() .
.
___________________________________ ______________________
7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие
условиям: 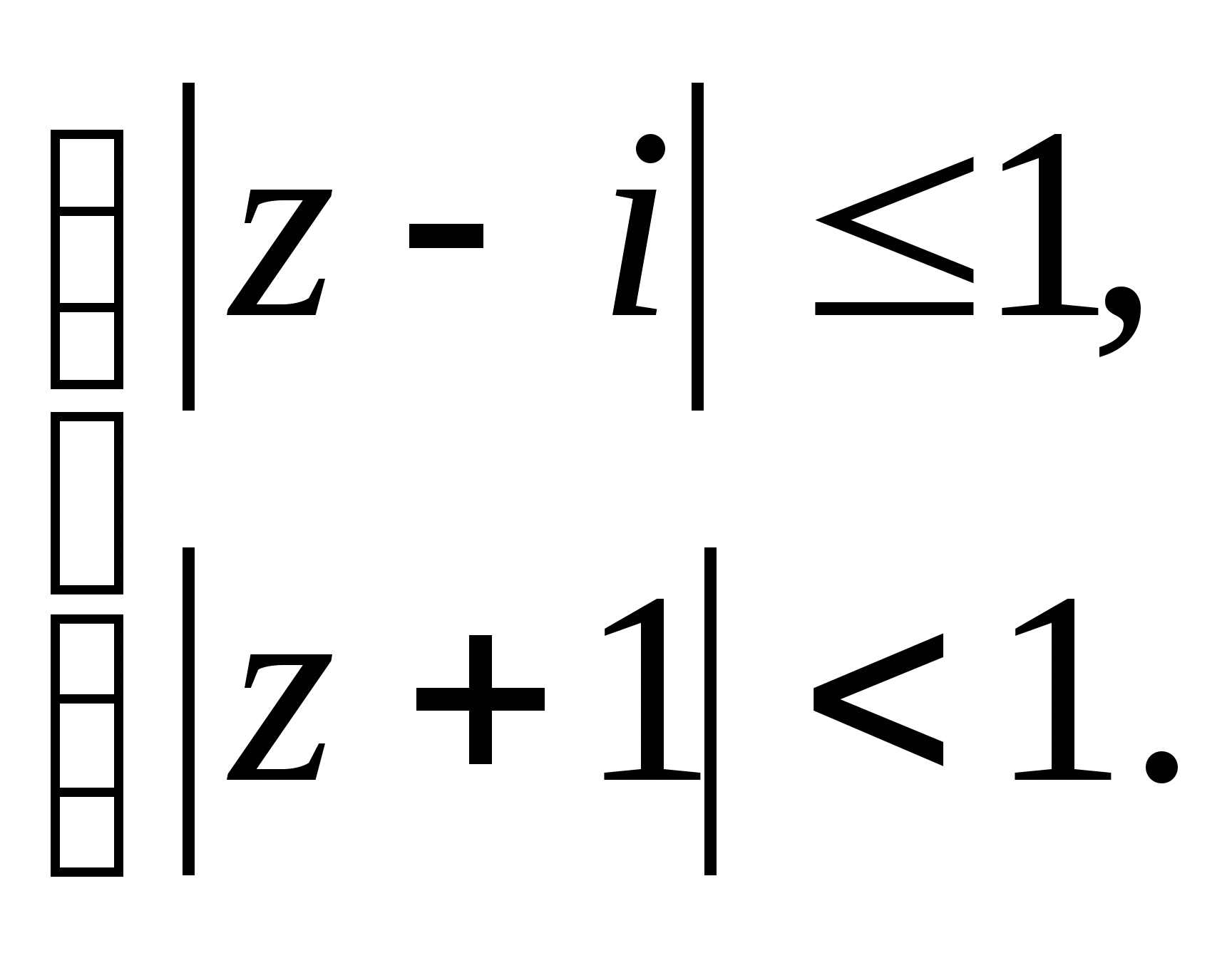
Вариант 2
-
Вычислите:
а)![]() , б)
, б)![]() .
.
-
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки ![]() ;
;
б) множество точек z, удовлетворяющих условию ![]()
в) множество точек z, удовлетворяющих условию ![]() .
.
-
Запишите комплексное число в стандартной тригонометри-
ческой форме: а)![]() , б)
, б)![]() .
.
-
Решите уравнение
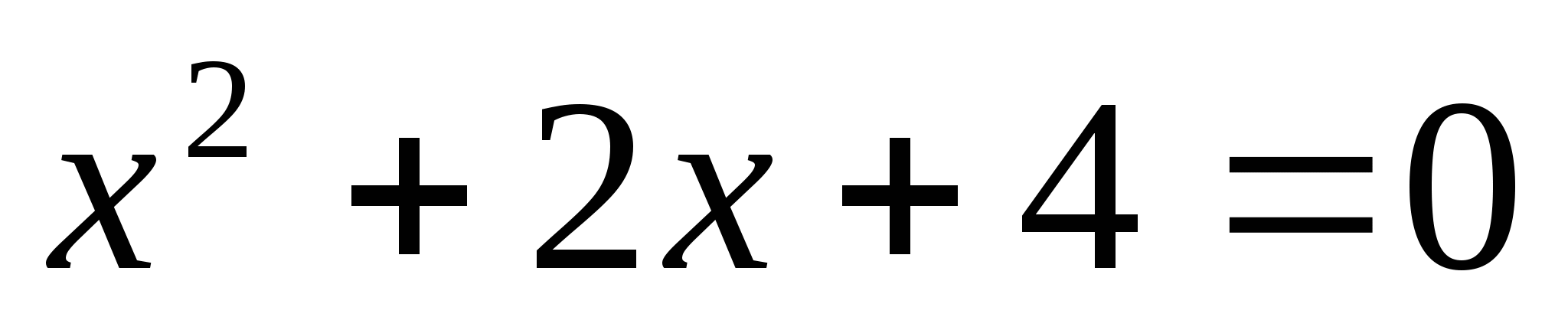 .
.
-
Вычислите
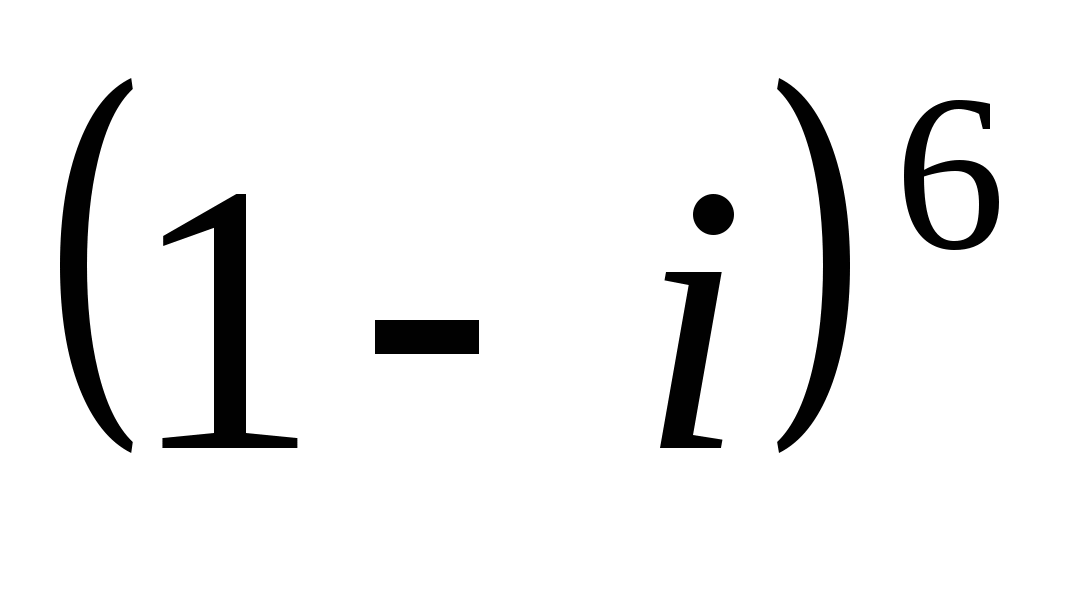 .
.
____________________________________________________________
6. Решите уравнение ![]() .
.
____________________________________________________________
7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие
условиям: 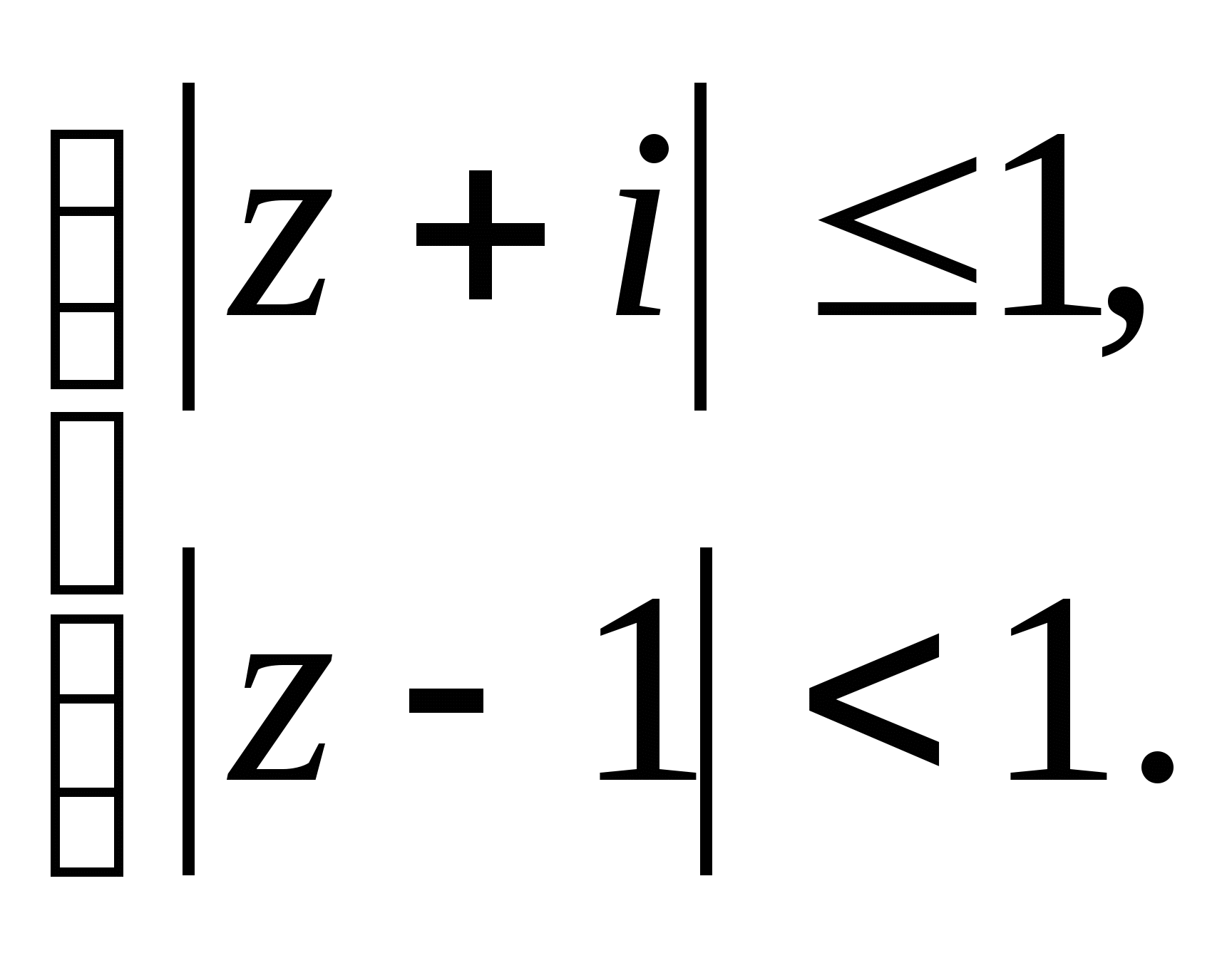
Контрольная работа № 7 (1 час)
Вариант 1
-
Напишите первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой
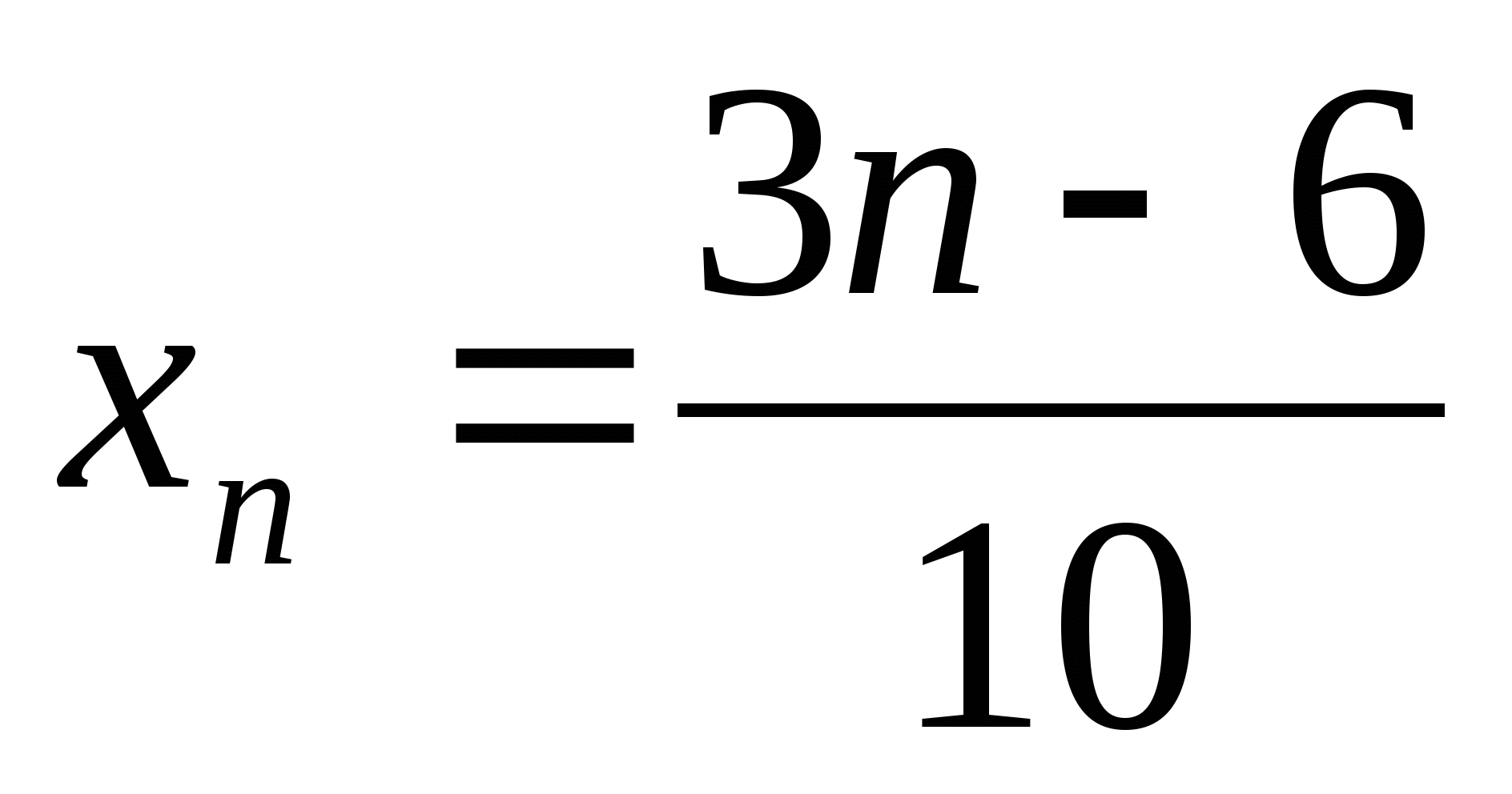 .
.
-
Исследуйте последовательность
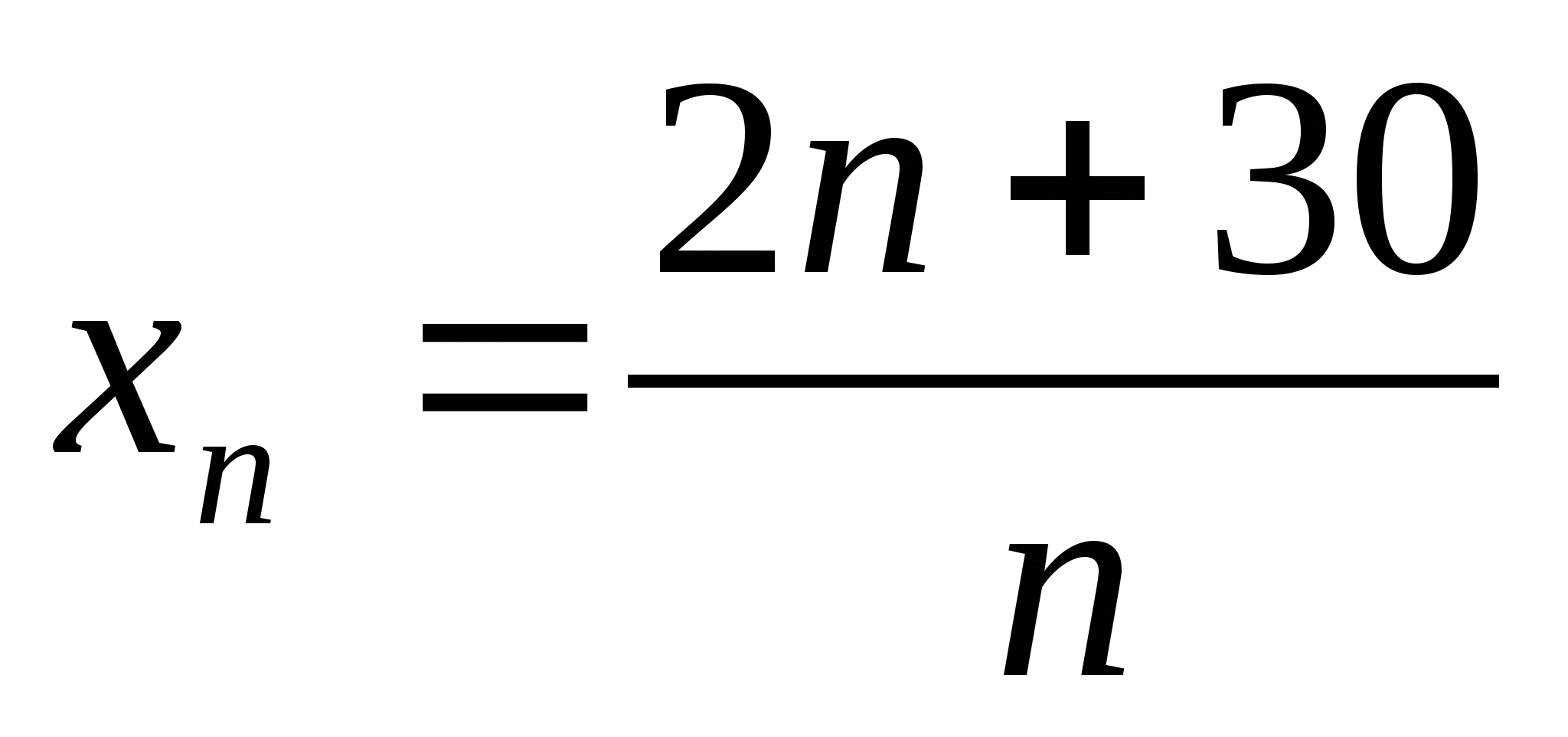 на ограниченность
на ограниченность
и на монотонность.
-
Вычислите: а)
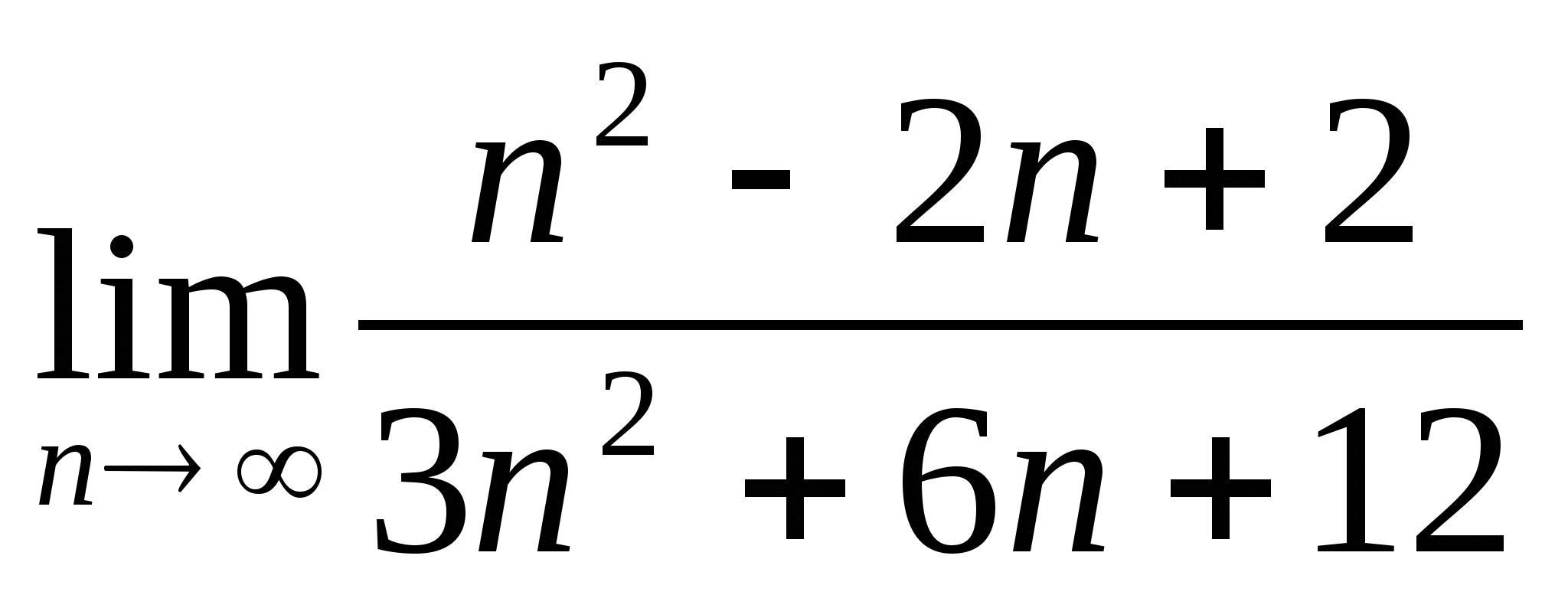 ; б)
; б) 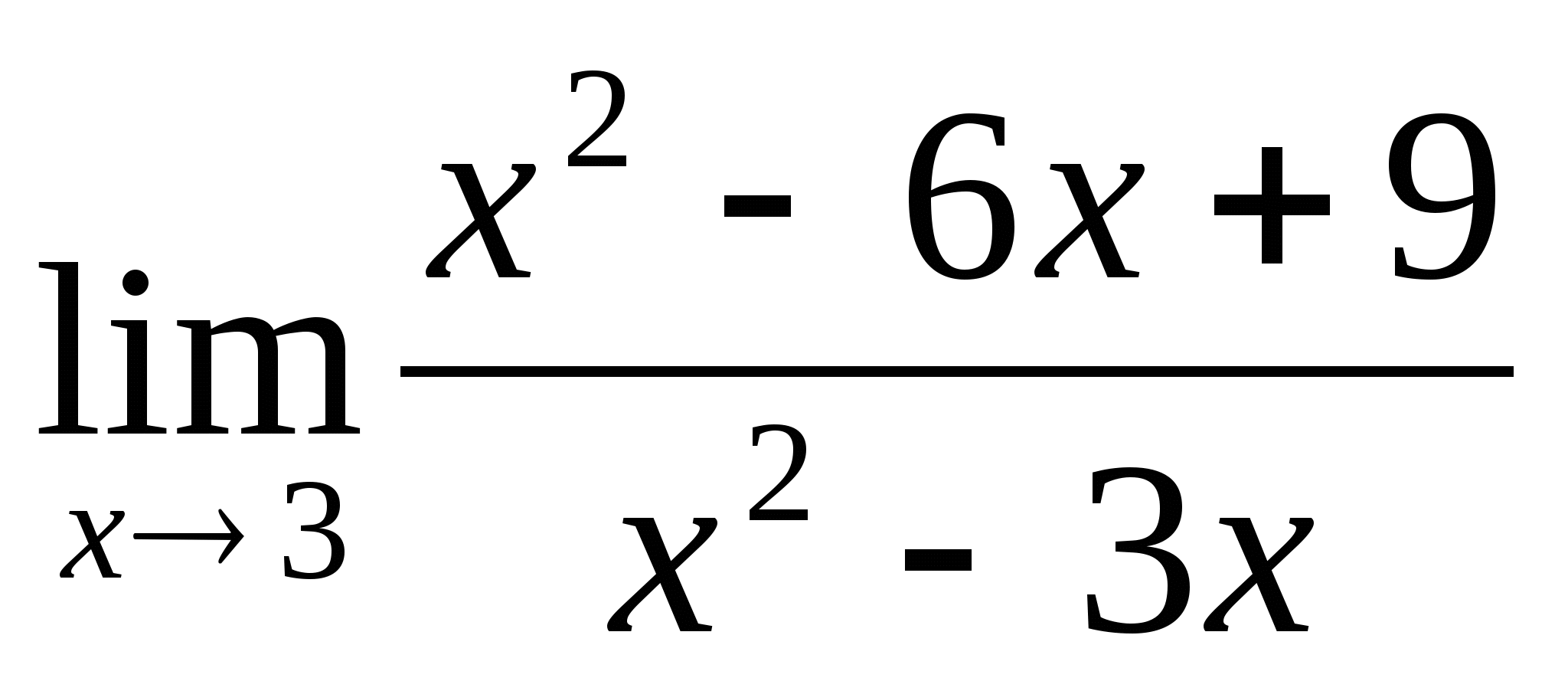 .
.
-
Пользуясь определением, выведите формулу дифференцирования
функции ![]() .
.
-
Пользуясь правилами и формулами дифференцирования, найдите
производную функции:
![]() .
.
-
Напишите уравнение касательной к графику функции
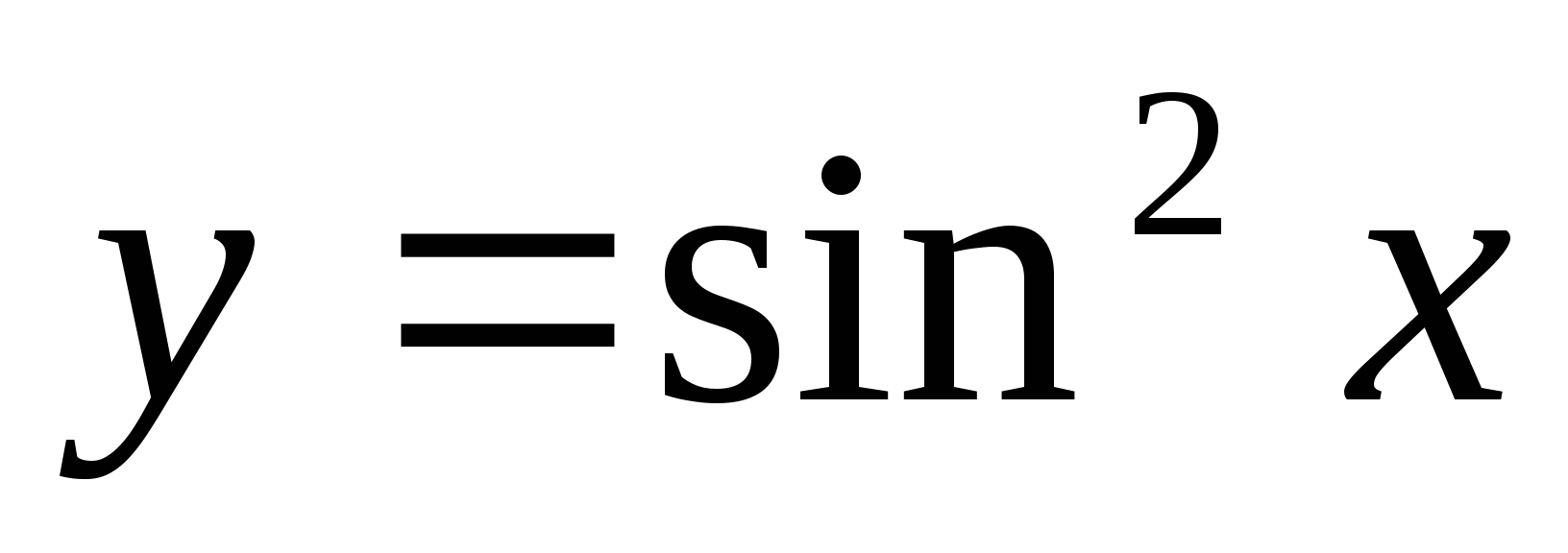 в точке
в точке
![]() .
. ![]()
___________________________________________________________
-
Докажите, что функция
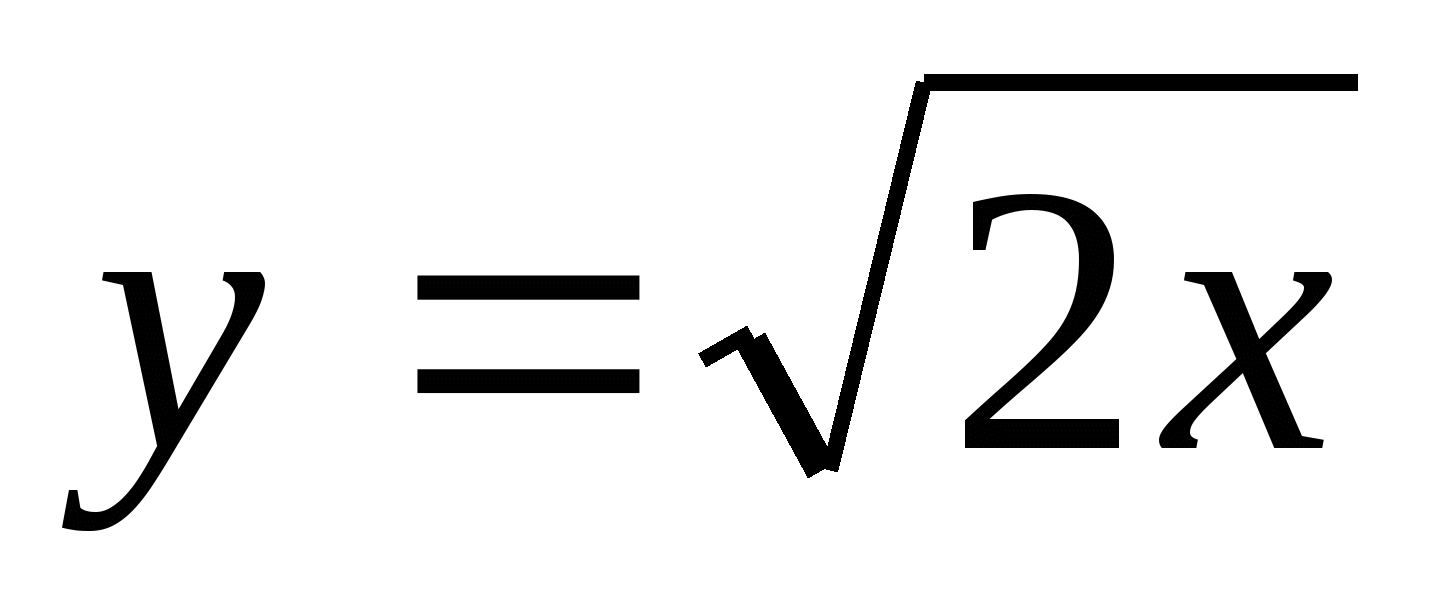 удовлетворяет соотношению
удовлетворяет соотношению
![]() .
.
___________________________________________________________
8. Найдите площадь треугольника, образованного осями координат
и касательной к графику функции ![]() в точке
в точке
![]() .
.
Вариант 2
-
Напишите первый, тридцатый и сотый члены последовательности, если
ее n-й член задается формулой ![]() .
.
-
Исследуйте последовательность
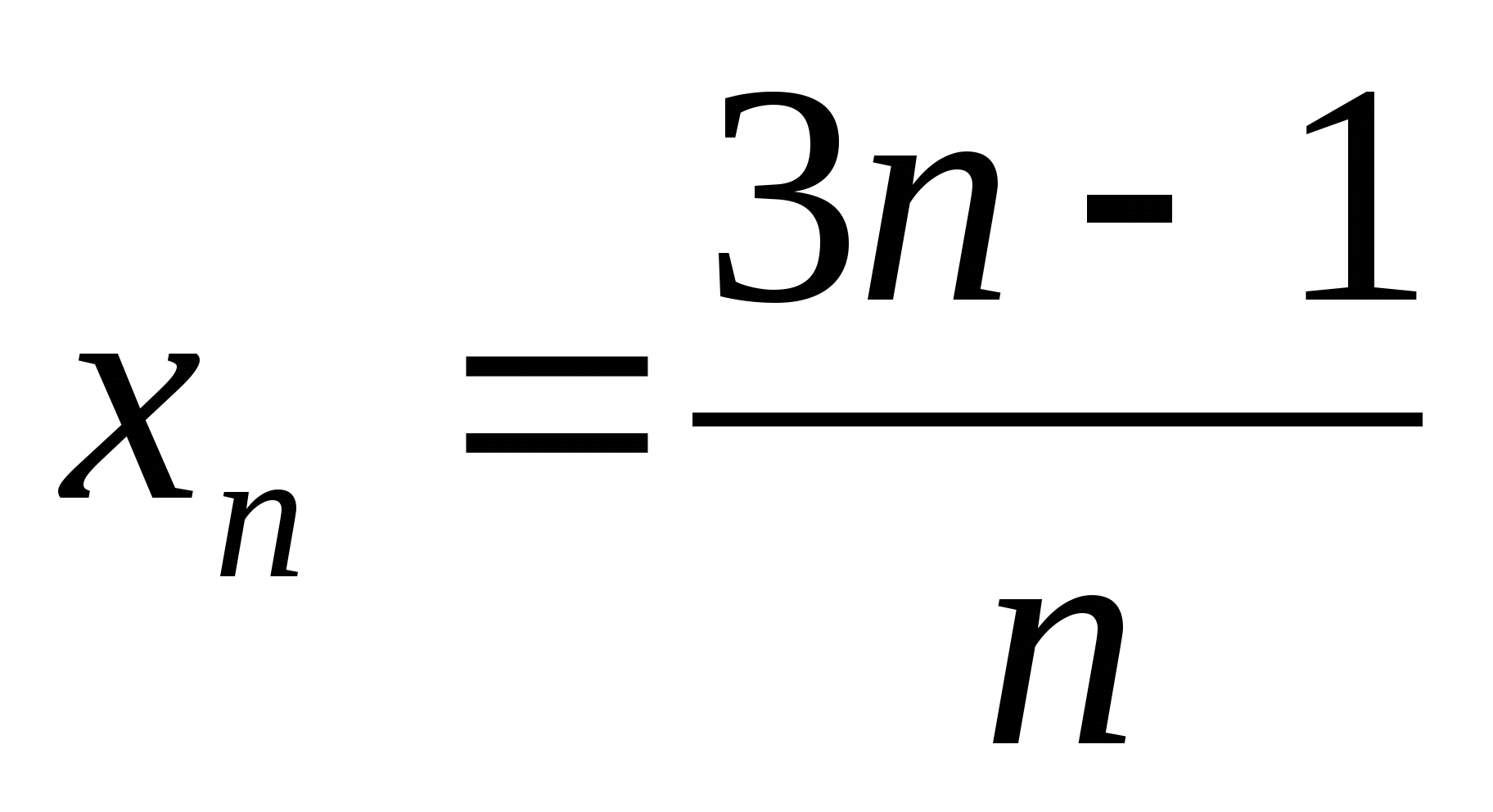 на ограниченность
на ограниченность
и на монотонность.
-
Вычислите: а)
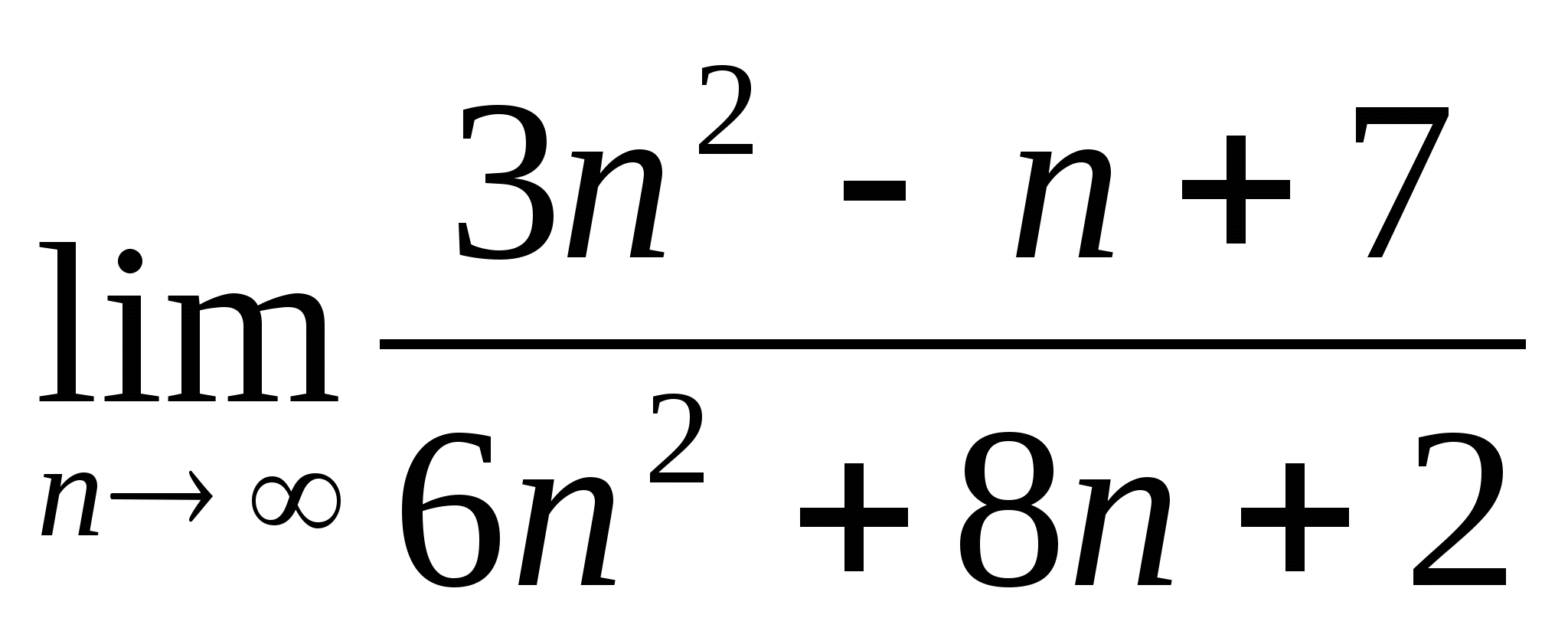 ; б)
; б) 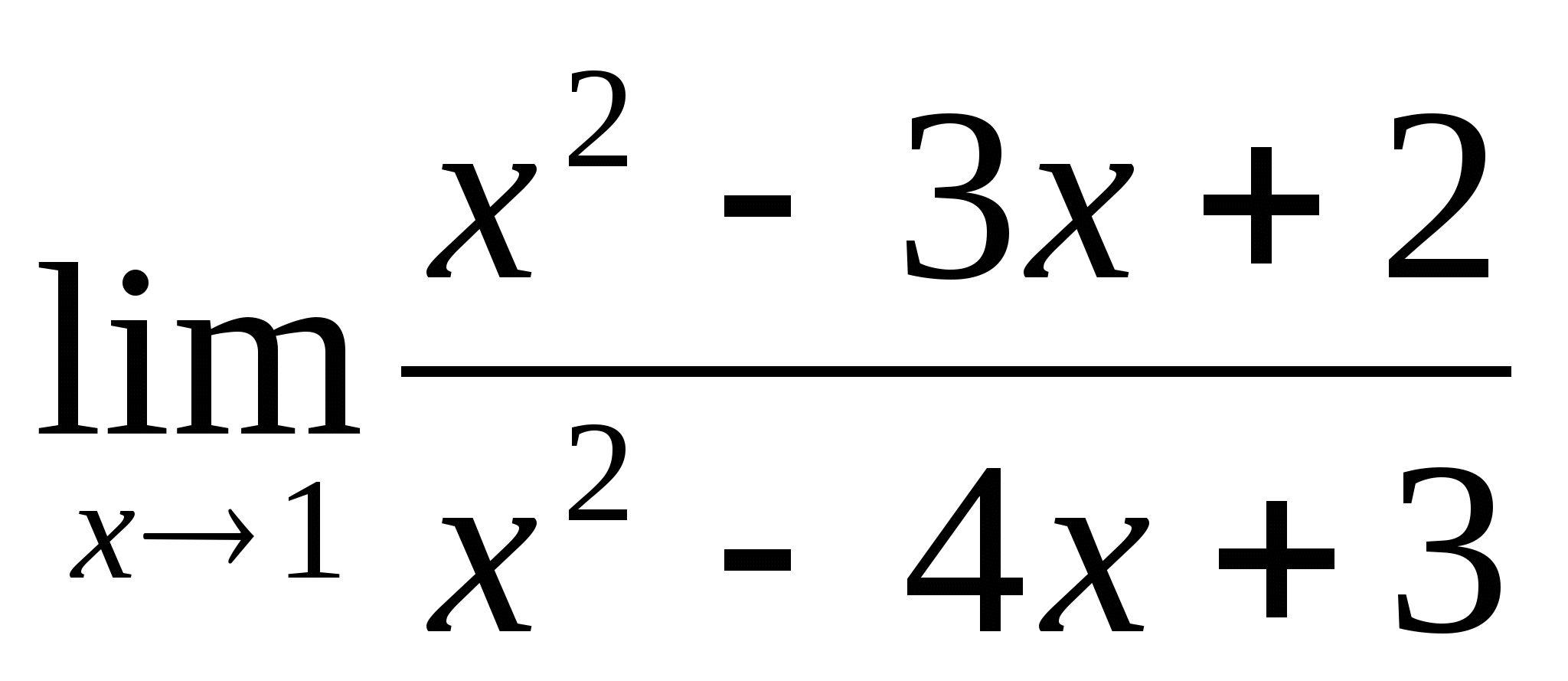 .
.
-
Пользуясь определением, выведите формулу дифференцирования
функции ![]() .
.
-
Пользуясь правилами и формулами дифференцирования, найдите
производную функции:
![]() .
.
-
Напишите уравнение касательной к графику функции
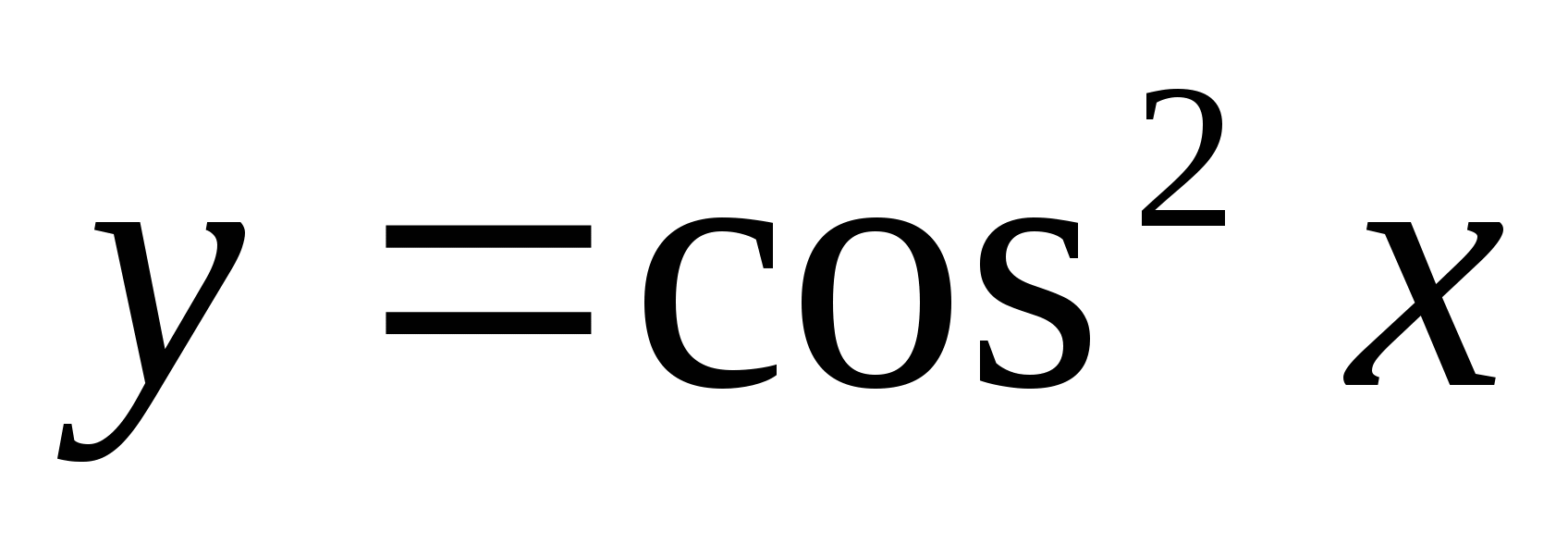
в точке ![]() .
.
________________________________________________________
7. Докажите, что функция ![]() удовлетворяет
соотношению
удовлетворяет
соотношению
![]() __
__
_________________________________________________________
8. Найдите площадь треугольника, образованного осями координат
и касательной к графику функции ![]() в точке
в точке
![]() .
.
Контрольная работа № 8 (2 часа)
Вариант 1
-
Исследуйте функцию
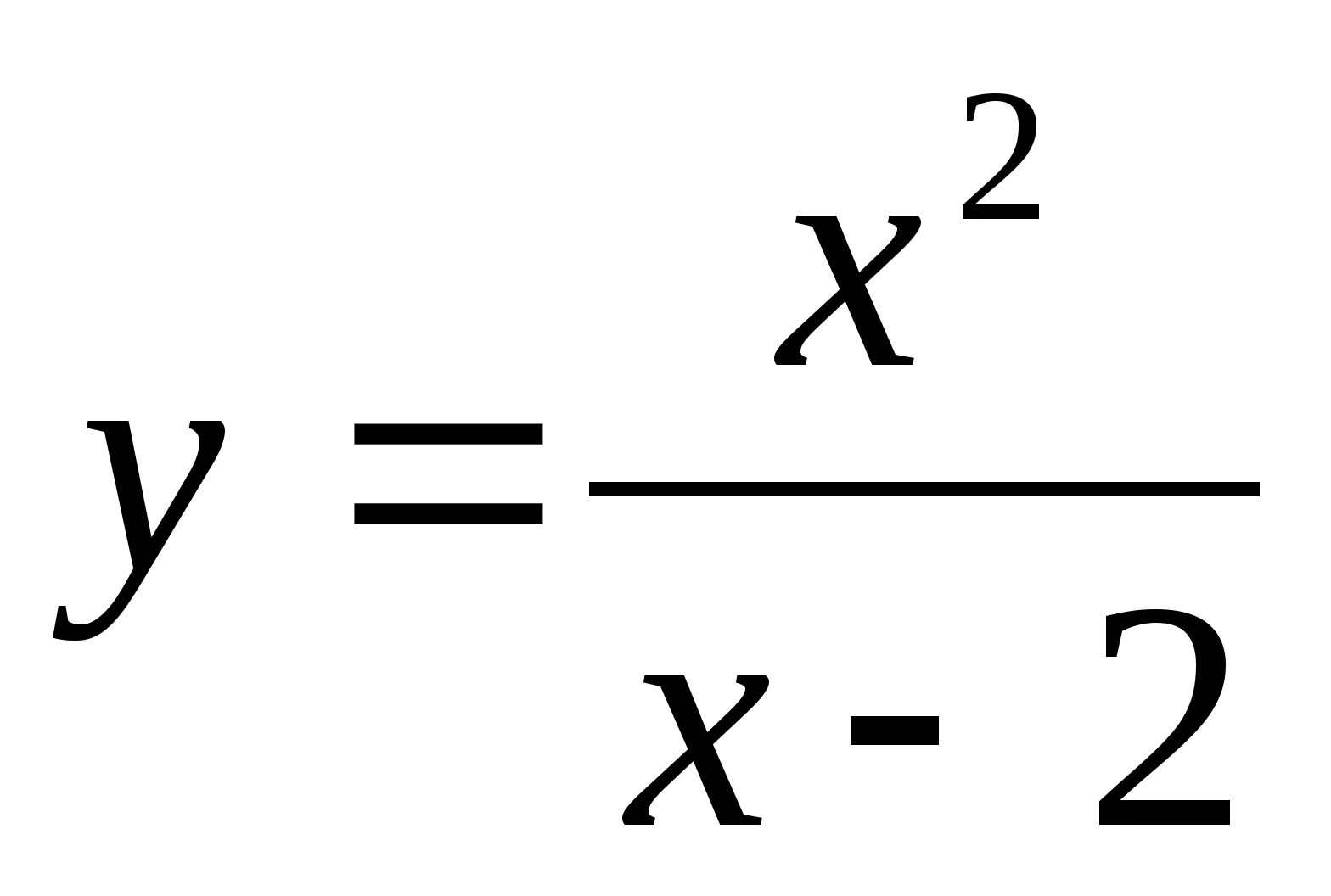 на
монотонность и экстремумы.
на
монотонность и экстремумы.
-
Постройте график функции
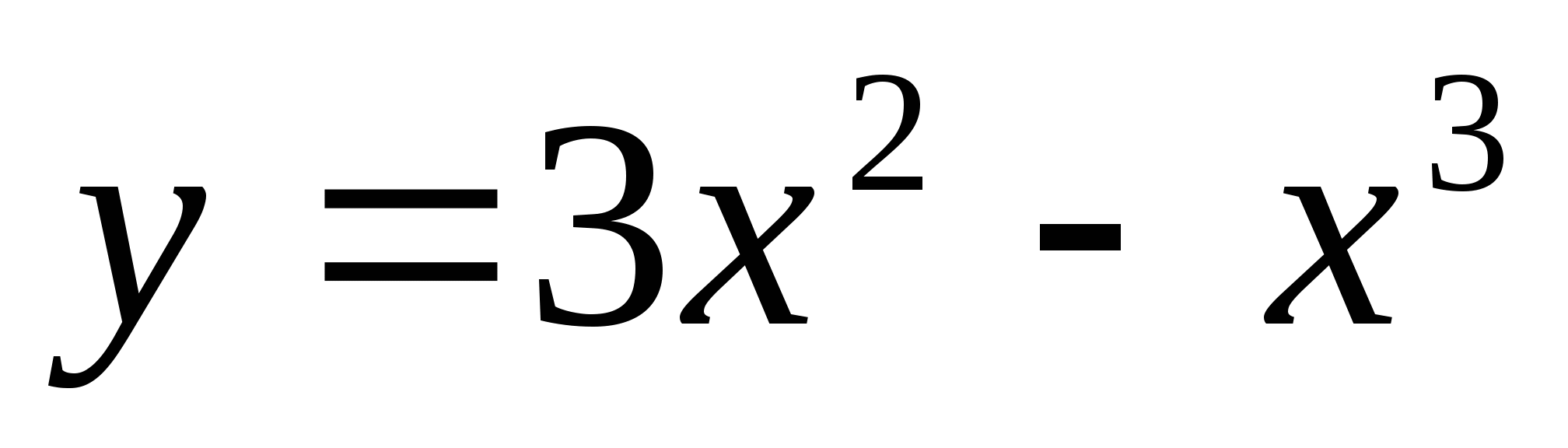 .
.
-
Найдите наименьшее и наибольшее значения функции
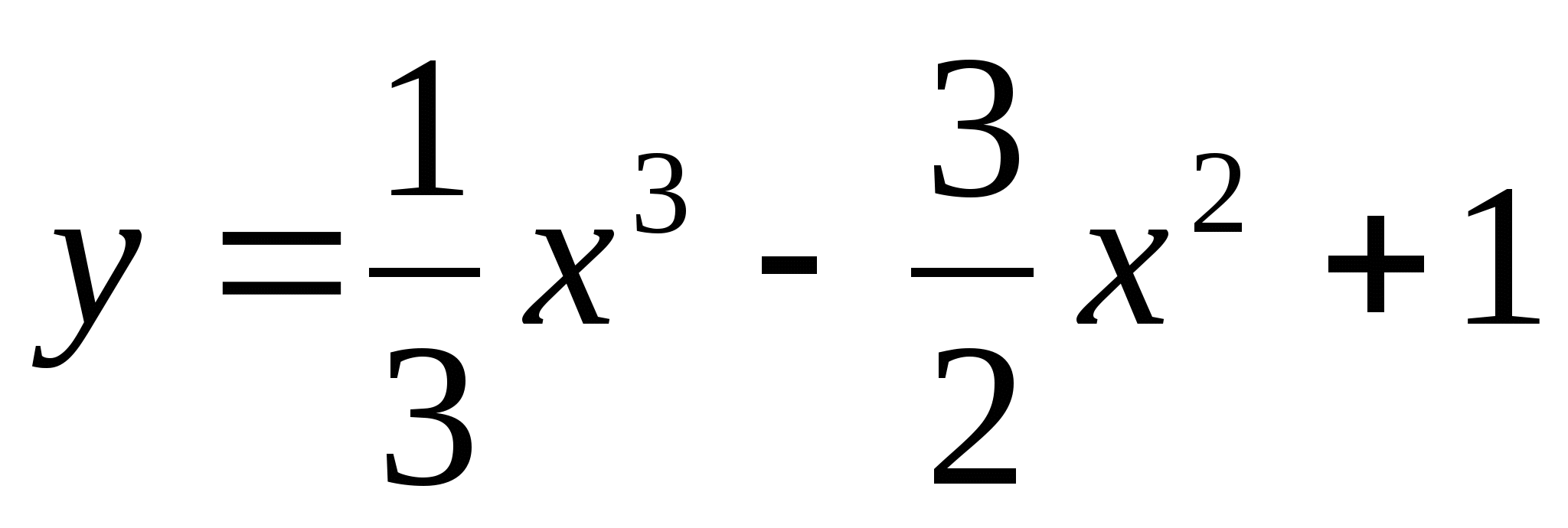
на отрезке ![]() .
.
-
В полукруг радиуса 6 см вписан прямоугольник. Чему равна его наибольшая площадь?

___________________________________________________________
-
Докажите, что при
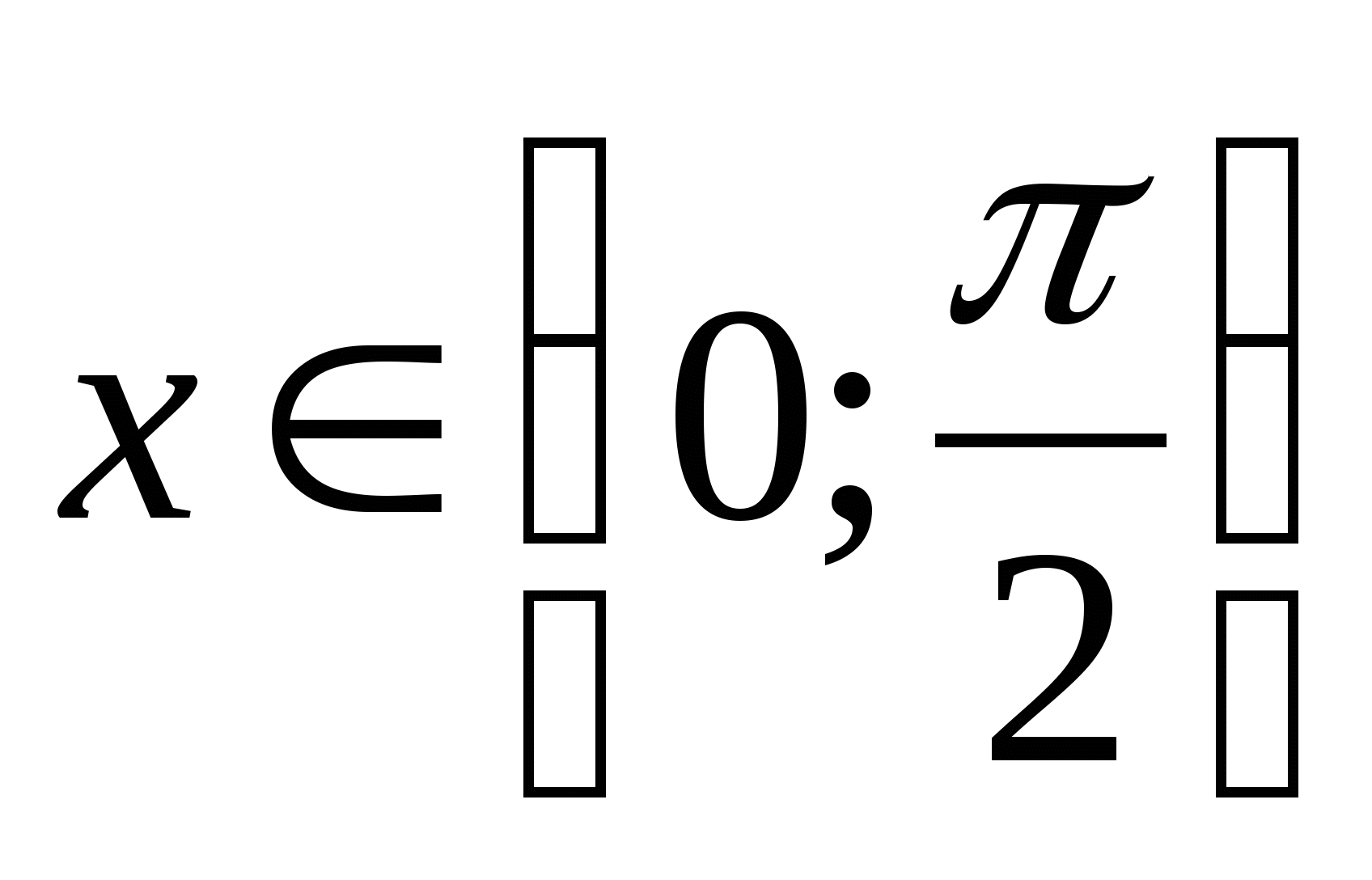 справедливо
неравенство
справедливо
неравенство 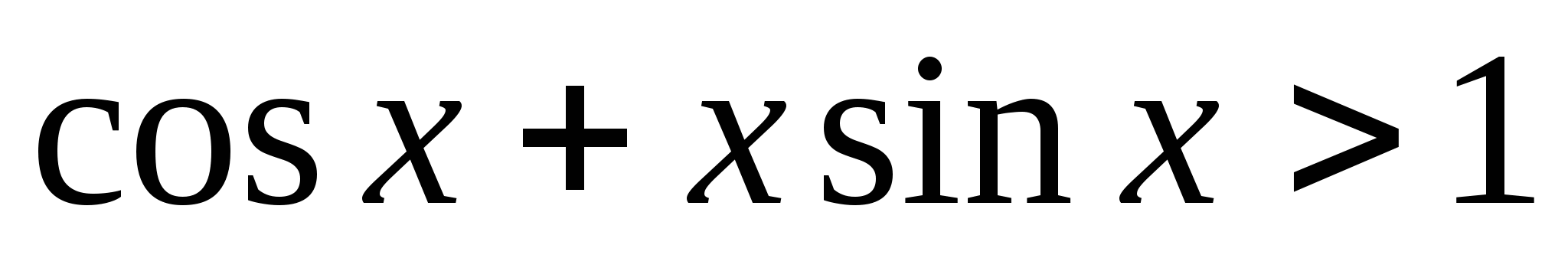 .
.
______________________________________________________________
-
При каких значениях параметра
 функция
функция
![]() убывает на всей числовой прямой?
убывает на всей числовой прямой?
Вариант 2
-
Исследуйте функцию
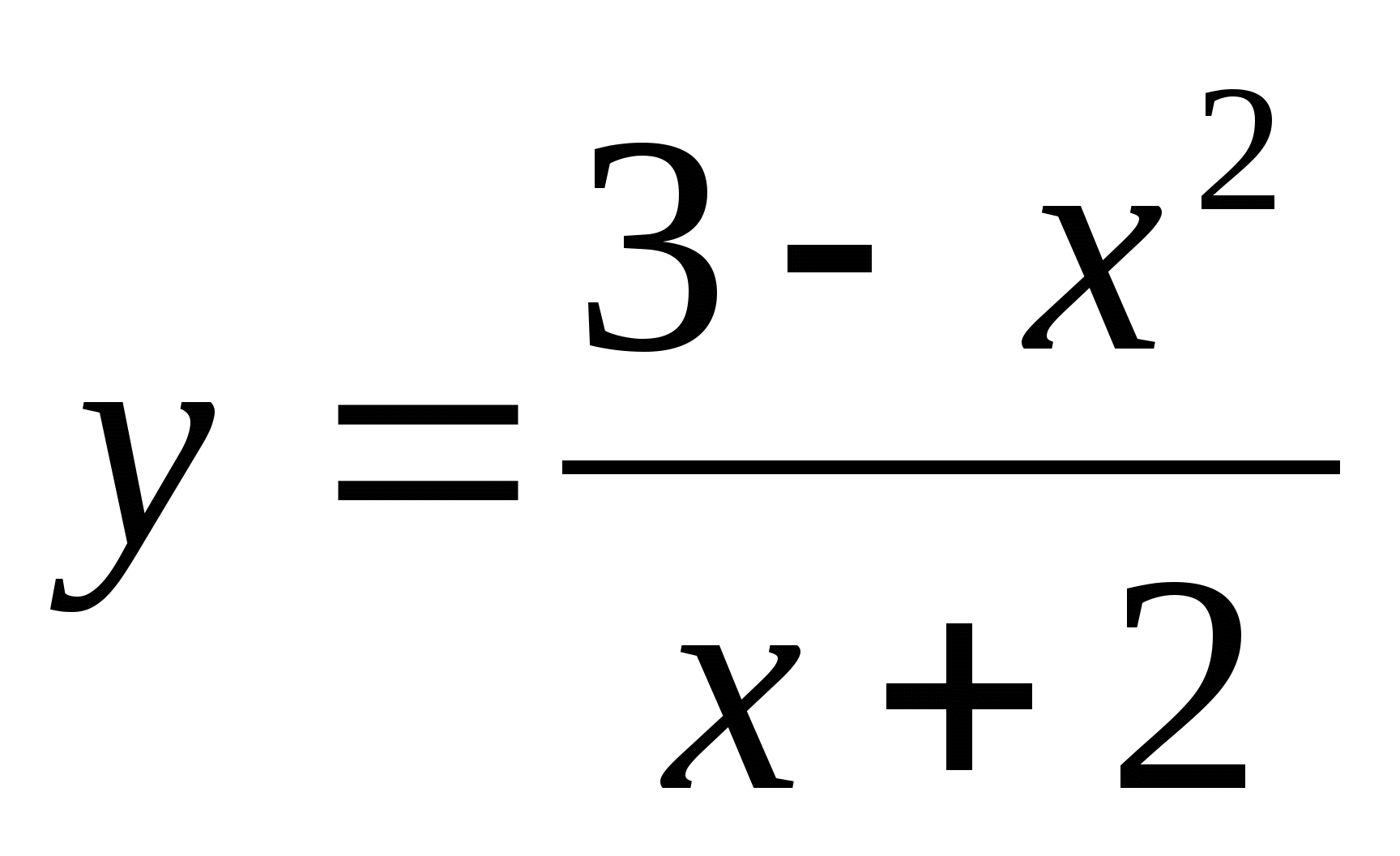 на
монотонность и экстремумы.
на
монотонность и экстремумы.
-
Постройте график функции
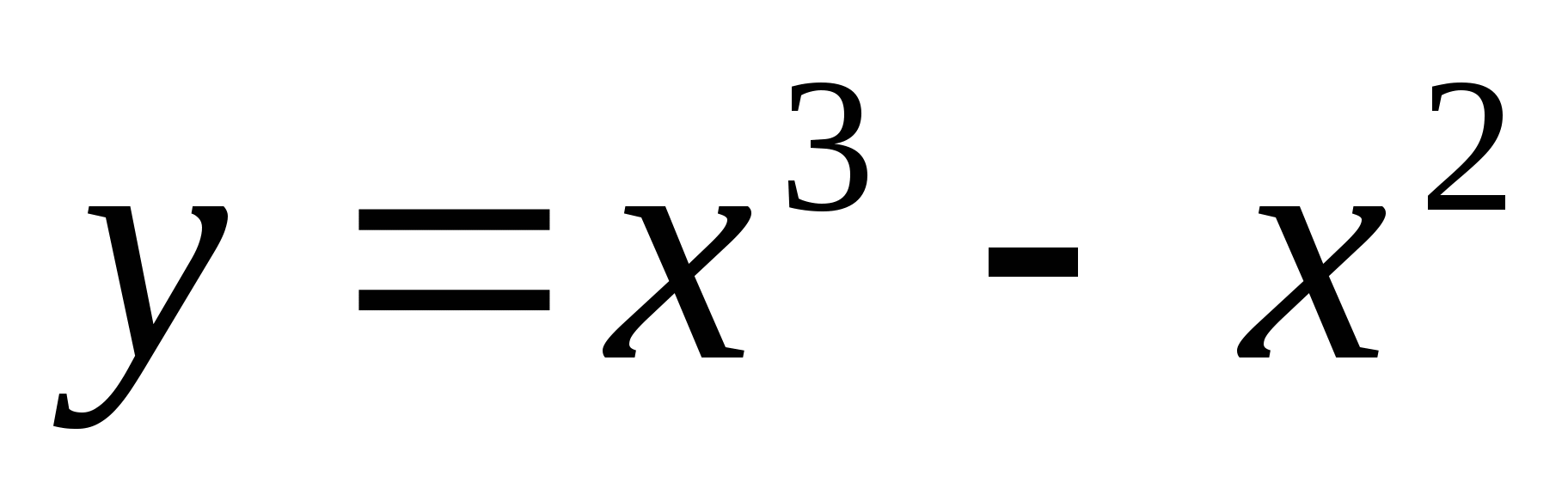 .
.
-
Найдите наименьшее и наибольшее значения функции
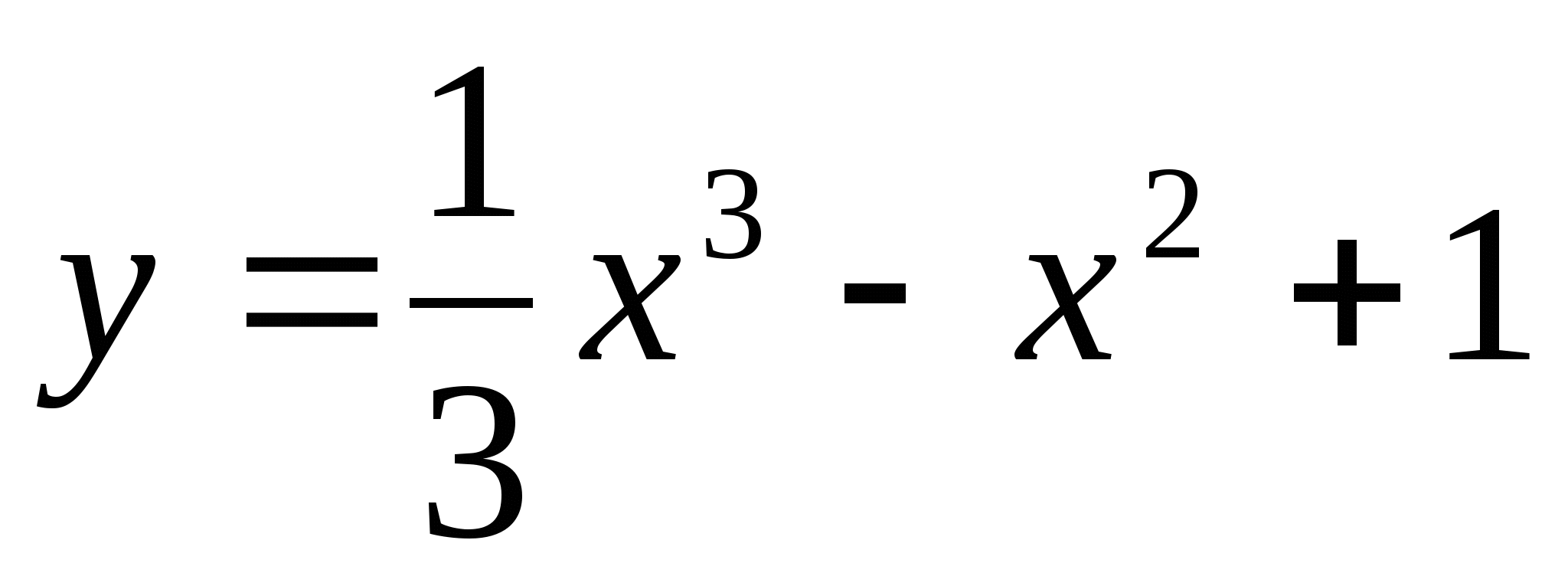 на отрезке
на отрезке 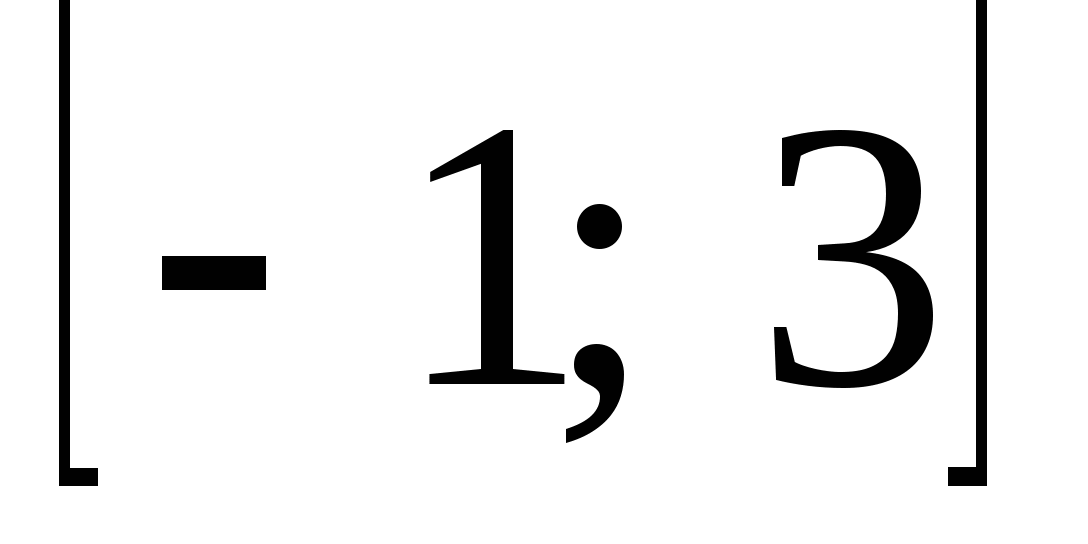 .
.
-
В прямоугольный треугольник с гипотенузой 8 см. и углом 60˚ вписан
прямоугольник так, что одна из его сторон лежит на гипотенузе.
Чему равна наибольшая площадь такого прямоугольника? ![]()
-
Докажите, что при
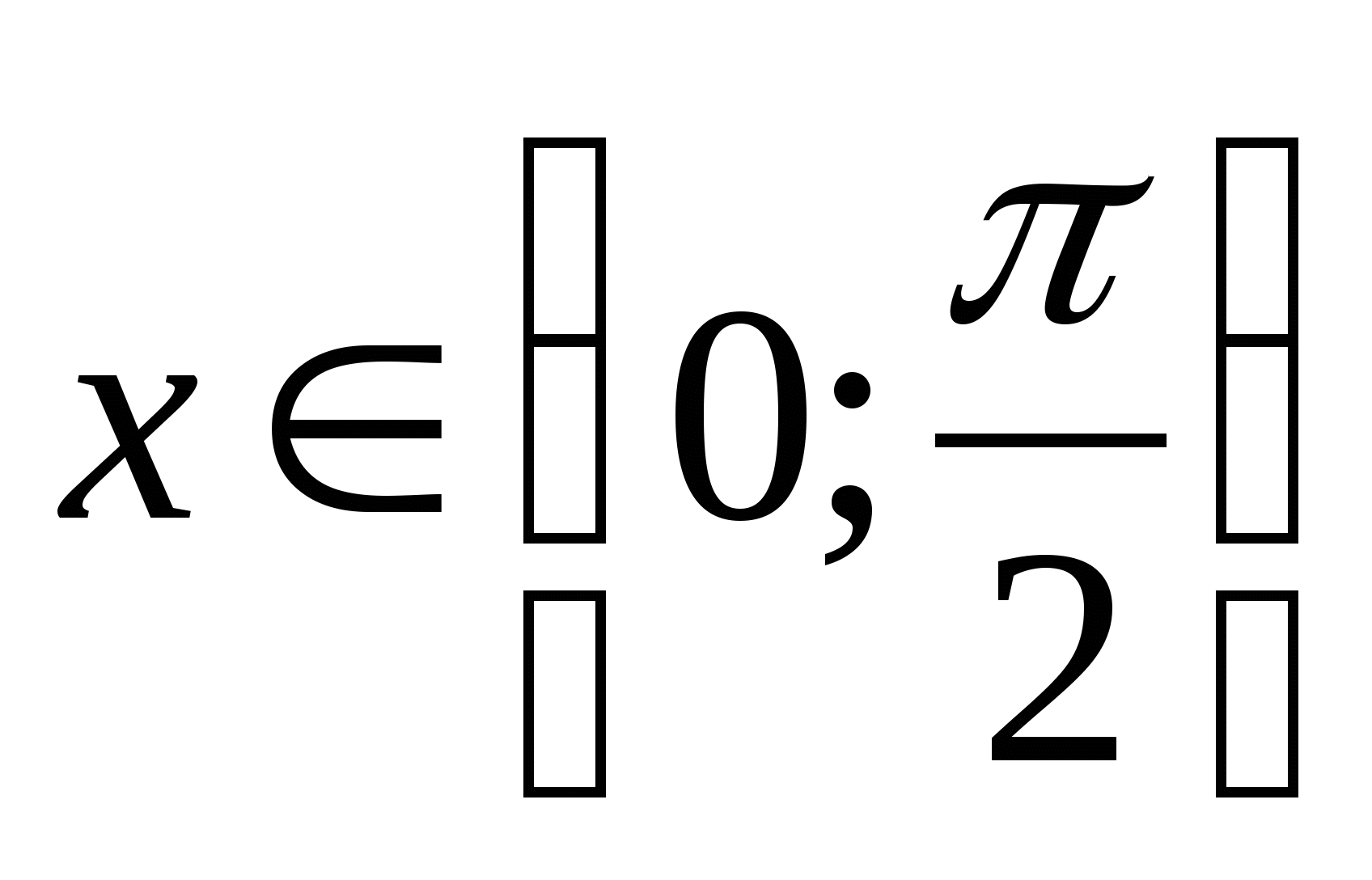 справедливо
неравенство
справедливо
неравенство 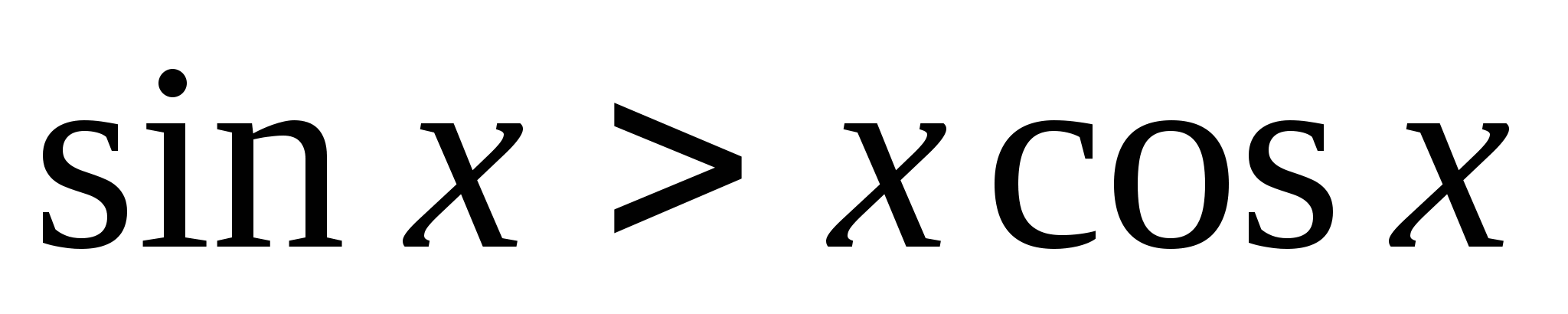 .
.
___________________________________________________________________
-
При каких значениях параметра
 функция
функция
![]() возрастает на всей числовой прямой?
возрастает на всей числовой прямой?
Контрольная работа № 9 (1 час)
Вариант 1
-
Сколькими способами можно составить трехцветный
полосатый флаг, если имеется материал 5 различных цветов?
-
Сколько четырехзначных чисел можно составить из цифр 1,2,3,4
при условии, что каждая цифра может содержаться в записи числа лишь нечетное число раз?
3. Решите уравнение ![]() .
.
4. Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом 2 туза?
_____________________________________________________
-
На прямой взяты 8 точек, а на параллельной ей прямой - 5 точек. Сколько существует треугольников, вершинами которых являются данные точки?
6. В разложении бинома ![]() коэффициент
третьего члена на 44 больше коэффициента второго члена. Найдите
член, не зависящий от
коэффициент
третьего члена на 44 больше коэффициента второго члена. Найдите
член, не зависящий от![]() .
.
Вариант 2
1. В яхт-клубе состоит 9 человек. Из них надо выбрать председателя, заместителя, секретаря и казначея. Сколькими способами это можно сделать?
-
Сколько четырехзначных чисел можно составить из цифр 1,2,3,0
при условии, что каждая цифра может содержаться в записи числа лишь 1 раз?
-
Решите уравнение
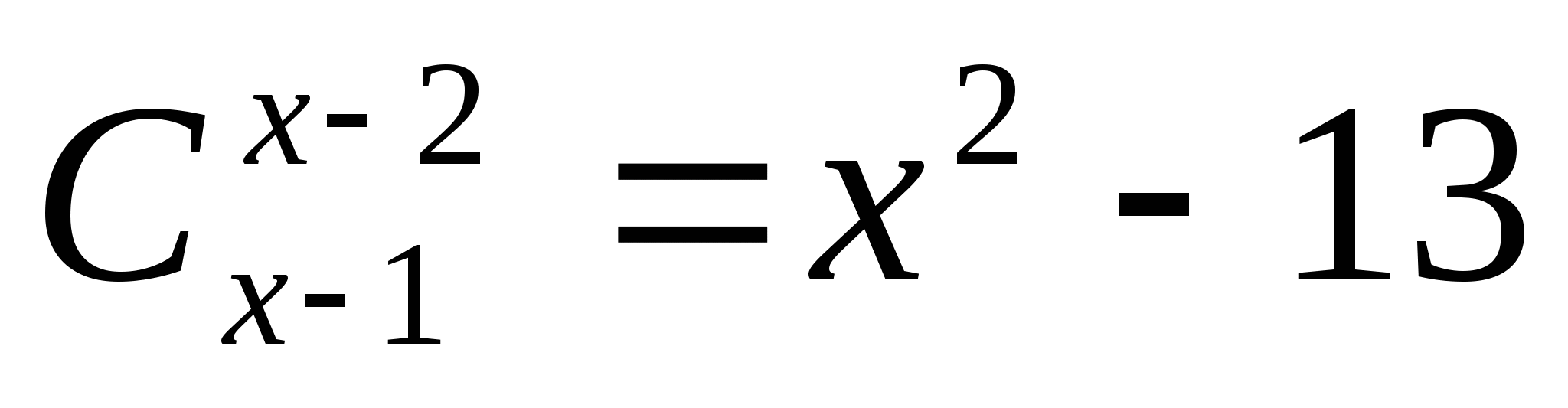 .
.
-
Из колоды в 36 карт вытаскивают три карты. Какова вероятность того, что все они тузы?
________________________________________________________
5. Сколько существует треугольников, у которых вершины
являются вершинами данного выпуклого 8-угольника, но стороны не совпадают со сторонами этого n-угольника?
6. Сумма биномиальных коэффициентов разложения бинома
![]() равна 64. Найдите член, не
зависящий от x.
равна 64. Найдите член, не
зависящий от x.
Контрольные работы по геометрии
10 класс
1). Основание АD трапеции АВСD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а). Каково взаимное расположение прямых
ЕF и АВ?
б). Чему равен угол между прямыми ЕF и АВ,
если ![]() АВС =
1500?
АВС =
1500?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а). Выполните рисунок к задаче;
б). Докажите, что полученный четырех -
угольник - ромб.
2 вариант
1). Треугольники АВС и АDС лежат в разных плоскостях и имеют общую сторону АС. Точка Р - середина стороны АD, точка К - середина DС.
а). Каково взаимное расположение прямых
РК и АВ?
б). Чему равен угол между прямыми РК и
АВ, если ![]() АВС = 400 и
АВС = 400 и
![]() ВСА = 80?
ВСА = 80?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, М
и N - середины сторон АВ и ВС
соответственно, Е ![]() СD, К
СD, К ![]() D, DА : ЕС = 1 :
2, DК : КА = 1 : 2.
D, DА : ЕС = 1 :
2, DК : КА = 1 : 2.
а). Выполните рисунок к задаче;
б). докажите, что четырехугольник МNЕК -
трапеция.
Контрольная работа № 2
1 вариант
1). Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая lпересекает плоскости α и β в точках А1 и А2 соответственно,прямая m - в точках В1 и В2. Найдите длину отрезка А2В2, еслиА1В1 = 12 см,В1О : ОВ2 = 3 : 4.
3). Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВСи DD1.
2 вариант
1). Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и βв точках А1 и А2 соответственно, прямая m - в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2= 15 см, ОВ1 : ОВ2 = 3 : 5.
3). Изобразите тетраэдр DABC и постройте его сечение
плоскостью, проходящей через точки M и N,
являющиеся серединами ребер DC и BC, и точку
K, такую, что K![]() DA, АK : KD =
1 : 3.
DA, АK : KD =
1 : 3.
Контрольная работа № 3
1 вариант
1). Диагональ куба равна 6 см. Найдите:
а).Ребро куба;
б).Косинус угла между диагональю куба и
плоскостью одной из его граней.
2). Сторона АВ ромба ABCD равна a, один
из углов равен 60°. Через сторону АВ проведена плоскость α
на расстоянии ![]() от точки D.
от точки D.
а). Найдите расстояние от точки С до плоскости α;
б). Покажите на рисунке линейный угол двугранного угла
DABM,М ![]() α.
α.
в) Найдите синус угла между плоскостью ромба и плоскостью α.
2 вариант
1). Основанием прямоугольного параллелепипеда служит квадрат,
диагональ параллелепипеда равна ![]() см, а его измерения относятся
как 1:1:2.Найдите:
см, а его измерения относятся
как 1:1:2.Найдите:
а).Измерения параллелепипеда;
б).Синус угла между диагональю параллеле -
пипеда и плоскостью его основания.
2). Сторона квадрата ABCD равна а. Через сторону
AD проведена плоскость α на расстоянии![]() от точки В.
от точки В.
а). Найдите расстояние от точки С до плоскости α.
б). Покажите на рисунке линейный угол
двугранного угла BADM,М ![]() α.
α.
в). Найдите синус угла между плоскостью
квадрата и плоскостью α.
Контрольная работа № 4
1 вариант
1). Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба;
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
2 вариант
1). Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2). Основанием прямого параллелепипеда
ABCDA1B1C1D1
является параллелограмм ABCD, стороны которого равны
![]() и 2а, острый угол равен 45°.
Высота параллелепипеда равна меньшей высоте параллелограмма.
Найдите:
и 2а, острый угол равен 45°.
Высота параллелепипеда равна меньшей высоте параллелограмма.
Найдите:
а). меньшую высоту параллелограмма;
б). угол между плоскостью АВС1 и плоскостью основания;
в). площадь боковой поверхности параллелепипеда;
г). площадь поверхности параллелепипеда.