Алгебра 9 класс. Мордкович. Геометрическая прогрессия 4-6 уроки

Класс

9

УМК (название учебника, автор, год издания)

Алгебра 9 класс Авт.: А.Г. Мордкович, М.: Мнемозина -2013

Уровень обучения

базовый

Тема урока

Сумма первых п членов

геометрической прогрессии

Общее количество часов, отведенное на изучение темы

6

Место урока в системе уроков по теме

4 урок по теме. Урок закрепления и применений знаний в новых условиях.

Цель урока

совершенствовать навыки решения задач.

Задачи урока

Общеобразовательные: закрепить навыки решения задач на нахождение суммы первых п членов геометрической прогрессии; формировать умения переносить знания в новую ситуацию.

Развивающие: развивать аналитическое мышление; познавательную активность мышления, умение работать с текстовой информацией.

Воспитательные: формирование умения работать самостоятельно.

Планируемые результаты

Учащиеся научатся:

находить суммы первых п членов геометрической прогрессии; формировать умения переносить знания в новую ситуацию.

аргументировать и обосновывать собственную позицию.

Техническое обеспечение урока

мультимедиапроектор, презентация по теме урока

Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы)

А.Г. Мордкович Алгебра . 9 класс.: В двух частях: Учеб. для общеобразовательных учреждений.-5-е изд. - М.: Мнемозина, 2013,

interneturok.ru/algebra/9-klass/algebra-9-klass-a-g-mordkovich; problems.ru/; https://math-oge.sdamgia.ru/

Содержание.

Урок 4

Сумма первых п членов

геометрической прогрессии

Ход урока

I. Организационный момент. Мотивация учебной деятельности.

II. Актуализация знаний обучающихся.

1. Устная работа.

1. Является ли геометрической прогрессией последовательность 5, 15, 45, 135.

2. Назовите два предыдущих и два последующих члена геометрической прогрессии, знаменатель которой равен 9.

…, …, 81, … .

3. (b_п) - геометрическая прогрессия.

а₂ = 7; а₇ = -224, q⁵ = -32.

а₁ - ? а₈ - ?

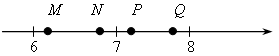
4. Какая из точек, отмеченных на координатной прямой, соответствует числу .

5. Какая из прямых не пересекает график функции у = ?

1) у = 4; 2) у = -4х; 3) х = -2; 4) у = 2х.

.

2. Работа у доски по карточкам (4 обучающихся).

Работают вместе с учителем, если возникает необходимость.

Карточка 1.

Найдите сумму первых четырех членов геометрической прогрессии (b_п), в которой b₁ = 6, b₄ = 24, q > 0.

Карточка 2.

Найдите сумму пяти первых членов геометрической прогрессии (b_п), в которой b₂ = 4, b₄ = 36, q < 0.

Карточка 3.

Найдите первый член геометрической прогрессии, в которой S₄ = 65, q = .

Карточка 4.

Найдите первый член геометрической прогрессии, в которой S₈ = 765, q = 2.

3. Проверочная работа (остальные обучающиеся).

Вариант I Вариант II

Рассматривается геометрическая прогрессия, заданная формулой п-го члена:

b_п = 16 · с_п = 27 ·

а) Найдите сумму ее первых пяти членов.

б) Найдите сумму ее первых п членов.

в) Сколько надо сложить последовательных членов этой прогрессии, начиная с первого, чтобы получить сумму, равную

? ?

III. Решение упражнений.

№ 17.49 (а; б).

а) Слагаемые в данной сумме составляют геометрическую прогрессию со знаменателем х. Так как х ≠ 1, то можно «свернуть» эту сумму, воспользовавшись формулой суммы геометрической прогрессии:

х + х² + х³ + … + х⁵⁰ = .

б) Слагаемые образуют арифметическую прогрессию, разность которой равна х. Поэтому

х + 2х + 3х + … + 100х = = 5050х.

IV. Подведение итогов.

- Сформулировать определение геометрической прогрессии.

- Назвать формулу п числа геометрической прогрессии.

- Назвать формулу суммы первых членов геометрической прогрессии (q = 1, q ≠ 1).

Домашнее задание.

П. 17 (п 3,4) № 17.47 (а) и № 17.39 (а)

Характеристическое свойство

геометрической прогрессии

Общее количество часов, отведённое на изучение новой темы

6

Место урока в системе уроков по теме

5 урок по теме. Урок изучения нового материала и систематизации знаний по теме.

Тип урока:

Комбинированный

Цель урока:

закрепить в ходе упражнений знание формул n-го члена геометрической прогрессии и суммы членов конечной геометрической прогрессии; доказать теорему, выражающую характеристическое свойство геометрической прогрессии; научить учащихся применять характеристическое свойство геометрической прогрессии при решении задач.

Задачи урока

образовательная: научиться систематизировать полученную информацию, научиться применять характеристическое свойство геометрической прогрессии при решении задач.

развивающая: развивать способность обобщать, замечать закономерности; анализировать.

воспитывающая: воспитывать внимание, аккуратность.

Планируемые результаты

Учащиеся научатся:

находить характеристическое свойство геометрической прогрессии; применять характеристическое свойство геометрической прогрессии при решении задач.

Техническое обеспечение урока

Персональный компьютер, мультимедийное оборудование, презентация по теме урока

Дополнительное методическое и дидактическое обеспечение урока

1. А.Г. Мордкович Алгебра . 9 класс.: В двух частях: Учеб. для общеобразовательных учреждений.-5-е изд. - М.: Мнемозина, 2013,

2. И.С. Петраков «Математика для любознательных». Москва «Просвещение», 2000г.

3. Я.И. Перельман «Занимательная алгебра».

4. images.yandex.ru/

Содержание.

У р о к 5

Характеристическое свойство

геометрической прогрессии

Ход урока

I. Организационный момент. Мотивация учебной деятельности.

Проверка домашнего задания.

1. Двое учащихся решают на доске № 17.47 (а) и № 17.39 (а) из домашнего задания.

2. Учитель выборочно проверяет домашние работы у некоторых учащихся.

II. Актуализация знаний обучающихся.

2. Устная работа.

а) b₁ = 2; q = 3. Найти b₄.

б)

в) b₃ = 12; b₅ = 48; q -?

г) Для каждого неравенства укажите множество его решений.

А) х² + 16 < х; Б) х² - 16 < 0; В) х² - 16 > 0.

1) ; 2) (-∞; -4) (4; +∞); 3) (-4; 4).

д) Упростите: .

е) Последовательность задана условием: с₁ = ; с_{п + 1} = ; с₈ -?

или

3. Решить устно № 17.13 (а); № 17.6 (б); № 17.7 (а; в); № 17.25 (а; в).

III. Изучение нового материала.

1. Проводим доказательство теоремы, выражающей характеристическое свойство геометрической прогрессии; записываем вывод:

2. Выполним преобразования равенства

Число называют средним геометрическим чисел а и b.

Таким образом, последнее равенство означает, что модуль любого члена геометрической прогрессии равен среднему геометрическому предыдущего и последующего членов.

3. Рассмотреть решение примера 11 на с.178 учебника. При каком значении х числа10х+7, 4х+6, 2х+3 образуют геометрическую прогрессию?

IV. Выполнение упражнений.

1. Решить № 17.31 (а; б) с комментированием на месте.

а) b₂ = 4; b₄ = 16; b₃ = (b₃  0).

b₃ = 8; q = b₃ : b₂ = 8 : 4 = 2; q = 2.

б) b₅ = 12; b₇ = 3; по условию b₆  0, тогда

q = b₇ : b₆ = 3 : (-6) =

О т в е т: а) 2; 8; б) -6.

2. Решить № 17.34 на доске и в тетрадях. Согласно характеристическому свойству

3х = 6х² - 6х; 6х² - 9х = 0; 3х(2х - 3) = 0; 3х = 0 или 2х - 3 = 0; х = 0 или х = 1,5.

Подставляя х = 0 в заданные выражения х - 1, 6х, находим соответственно -1; 0; 0 - это не геометрическая прогрессия.

Подставляя х = 1,5 в заданные выражения находим 0,5; 9 - это конечная геометрическая прогрессия со знаменателем

О т в е т: 1,5.

3. Самостоятельно решить № 17.33 (с проверкой).

Согласно характеристическому свойству (3у)² = -81  (-1); 9у² = 81;

у² = 9; у₁ = -3; у₂ = 3.

О т в е т: -3; 3.

4. Решить № 17.43 на доске и в тетрадях.

1; b₂; b₃; b₄; 81. Отсюда b₁ = 1; b₅ = 81; найдем q.

b₅ = b₁  q⁴; 81 = 1  q⁴; q⁴ = 3⁴ или q⁴ = (-3)⁴;

тогда q = 3 или q = -3.

1) Если q = 3, то 1; 3; 9; 27; 81.

2) Если q = -3, то 1; -3; 9; -27; 81.

О т в е т: 1; 3; 9; 27; 81 или 1; -3; 9; -27; 81.

5. Решить № 17.29 (в; г). Решение № 17.29 (г) объясняет учитель.

в) b₃ = 1; b₅ = (q > 0). Найти S₅.

г) b₇ = 27. Найти S₅.

Найдем b₅ = b₄  q = Применим формулу (II).

О т в е т: в) г)

6. Решить № 17.29 (а) самостоятельно.

V. Итог урока. Рефлексия.

Какой отметкой Вы бы оценили деятельность учителя на уроке?

Какую оценку Вы поставите за урок себе?

Домашнее задание: изучить материал на с. 177-180 учебника; решить № 17.31 (в; г); № 17.32, № 17.23; № 17.29 (б).

Класс

9

УМК (название учебника, автор, год издания)

Алгебра 9 класс Авт.: А.Г. Мордкович, М.: Мнемозина -2013

Уровень обучения

базовый

Тема урока

Прогрессии и банковские расчеты

Общее количество часов, отведенное на изучение темы

6

Место урока в системе уроков по теме

6 урок по теме. Урок изучения нового материала

Цель урока

познакомить обучающихся с понятием простого и сложного процентов; совершенствовать умения выполнять процентные расчеты. учить решать более сложные задачи, связанные с геометрической прогрессией.

Задачи урока

.

Общеобразовательные: познакомить учащихся с формулами простых и сложных процентов в ходе решения реальных практических задач; формировать умения переносить знания в новую ситуацию.

Развивающие: развивать умение сравнивать, выявлять закономерности, обобщать; развивать логическое мышление и творческую сторону мыслительной деятельности, развивать математически грамотную речь;

Воспитательные: формирование умение соотносить свои действия с планируемыми результатами.

Планируемые результаты

Учащиеся научатся:

находить простые и сложные проценты; выполнять процентные расчеты, решать более сложные задачи, связанные с геометрической прогрессией.

Техническое обеспечение урока

мультимедиапроектор, презентация по теме урока

Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы)

А.Г. Мордкович Алгебра . 9 класс.: В двух частях: Учеб. для общеобразовательных учреждений.-5-е изд. - М.: Мнемозина, 2013,

interneturok.ru/algebra/9-klass/algebra-9-klass-a-g-mordkovich; problems.ru/; https://math-oge.sdamgia.ru/</</u>

Урок 6

Прогрессии и банковские расчеты

Ход урока

1. Организационный момент.

Самоопределение. Мотивация учебной деятельности учащихся

- Добрый день.

- Как вы понимаете слова:

«Хоть выйди ты не в белый свет,

А в поле за околицей,-

Пока идешь за кем-то вслед,

Дорога не запомнится.

Зато, куда б ты ни попал

И по какой распутице,

Дорога та, что сам искал,

Вовек не позабудется» Н. Рыленков?

- Если вы готовы проявить настойчивость, старание и и самостоятельность в добывании знаний, мы можем приступить к работе.

II. Актуализация знаний обучающихся.

Устная работа.

1. Является ли геометрической прогрессией последовательность 5, 15, 45, 135.

2. Назовите два предыдущих и два последующих члена геометрической прогрессии, знаменатель которой равен 9.

…, …, 81, … .

3. (b_п) - геометрическая прогрессия.

а₂ = 7; а₇ = -224, q⁵ = -32.

а₁ - ? а₈ - ?

4. Какая из точек, отмеченных на координатной прямой, соответствует числу .

5. Какая из прямых не пересекает график функции у = ?

1) у = 4; 2) у = -4х; 3) х = -2; 4) у = 2х.

Проверка домашнего задания - фронтально. № 17.31 (в; г); № 17.32, № 17.23; № 17.29 (б).

III. Изучение нового материала.

1. а) Повторить определение процента.

б) Вспомнить, как проценты выражаются десятичными дробями:

1 % - это или 0,01;

25 % - это или 0,25;

4 % - это или 0,04;

0,3 % - это или 0,003;

106 % - это или 1,06.

в) Выполнить устно № 636 (а; г).

г) Вспомнить типы задач: процент от числа, число по его проценту.

2. Разобрать примеры стр. 180-181 учебника. (Это задачи реального содержания, в ходе решения которых принимаются две различные схемы начисления процентов.)

IV. Закрепление изученного материала.

№ 637 (а; б) из учебника Дорофеева

а) 20 % это 0,2, то повышение цены а (р.) на 20 % означает ее увеличение на 0,2а, то есть новая цена альбома а + 0,2а = 1,2а.

Дополнительный вопрос: во сколько раз новая цена больше прежней?

б) Если прежняя цена а р. составляет 100 %, то новая цена составляет 100 % - 65 % = 35 % от прежней и равна 0,35а.

№ 734, № 688.

№ 688.

Плата за завтраки увеличивается в арифметической прогрессии:

а₁ = 240, d = 240 · 0,02 = 4,8.

а) Декабрь: сентябрь - а₁;

октябрь - а₂;

ноябрь - а₃;

декабрь - а₄.

а₄ = 240 · 4,8 · 3 = 254,4 (р.)

б) S₄ = = 988,8 (р.)

№ 17.35 самостоятельно

V. Подведение итогов. Сделать подборку задач на проценты из ГИА

VI. Рефлексия учебной деятельности

- О чем задумались сегодня, работая над предложенным материалом?

- Какие практические навыки приобрели?

- Мое настроение после урока…

Домашнее задание. Сделать подборку задач на простые и сложные проценты из ГИА

подготовиться к контрольной работе, повторив материал § 16 и § 17; решить № 16.23 (б; в); № 16.34 (а; б); № 16.45; № 17.18 (а; в); № 17.26 (б).