Урок № 3

Тема уроку « Похідна функції її геометричний та фізичний зміст»

Мета уроку:

• домогтися засвоєння означення похідної;

• сформувати значення похідної під час обґрунтування формул для обчислення похідних деяких функцій;

• сформувати поняття похідної в точці, операція диференціювання

• загальна схема знаходження похідної в заданій точці;

• сформувати геометричний та фізичний зміст похідної;

• сформувати вміння знаходити кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці,знайти швидкість зміни величини в точці.

• розвивати логічне мислення ; навички контролю, самоконтролю та взаємоконтролю; спонукати до творчої діяльності.

• виховувати любов до рідної мови та предмету; працьовитість, відчуття колективізму та відповідальності; вміння самостійно приймати рішення.

Тип уроку : засвоєння нових знань і вмінь

Методи навчання : пізнавально-практичні

Предметні зв'язки: геометрія, фізика, астрономія.

Матеріальне забезпечення уроку:

- таблиці, комп`ютер, мультимедійний проектор;

- картки-завдання ;

- додатки до теми «похідна та її застосування»

Хід уроку

І. Організаційний момент.

а) Перевірка відсутніх.

б) Перевірка готовності до уроку.

ІІ. Перевірка домашнього завдання.

Вибірково перевіряємо виконання домашнього завдання в учнів які потребують додаткової педагогічної уваги за матеріалом вивчених тем проводимо тестування

№ 2

=

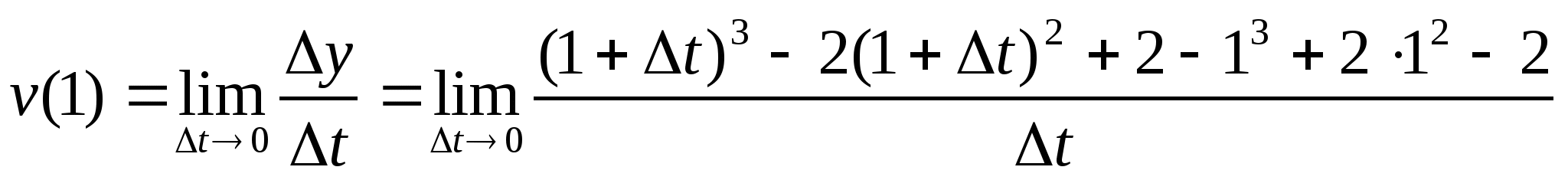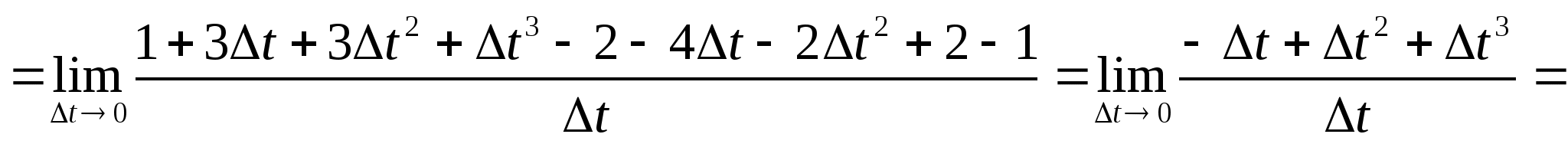
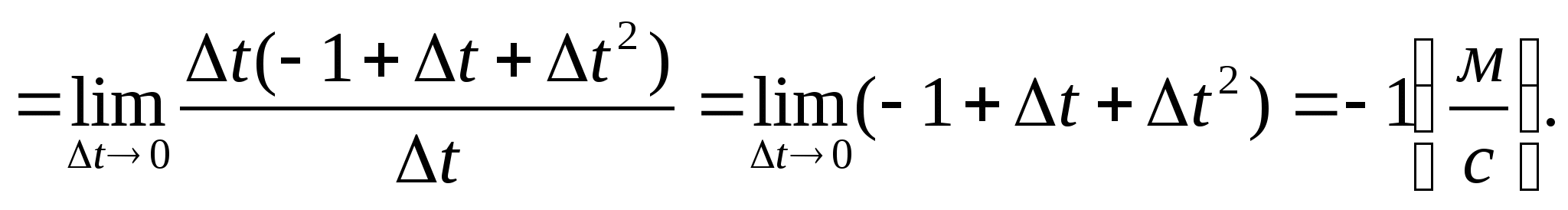
№ 9

.

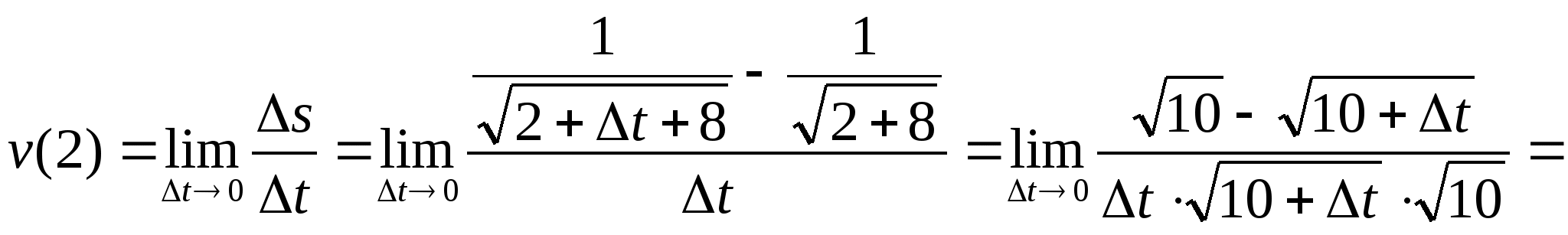
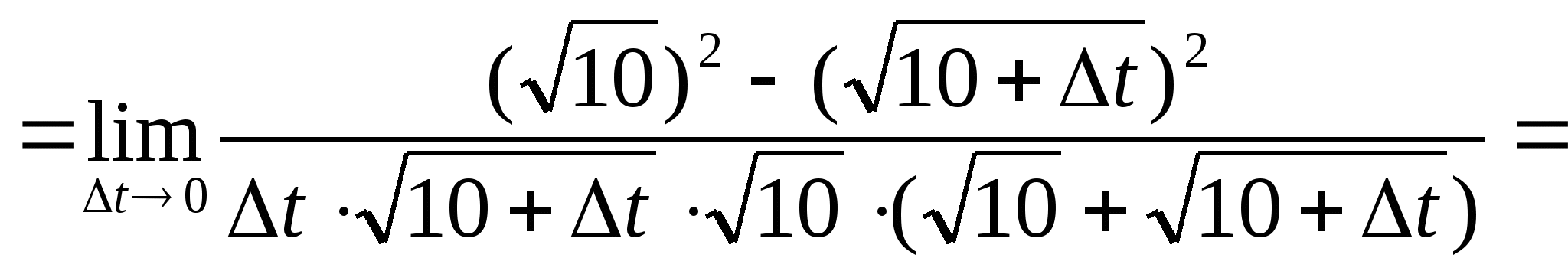
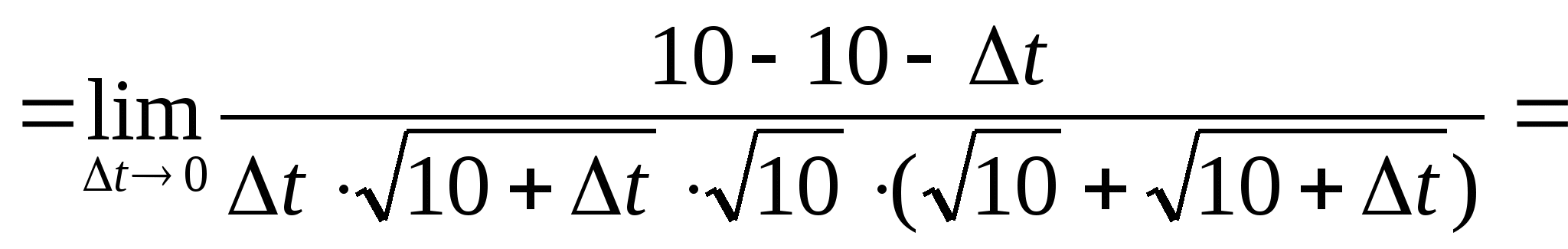
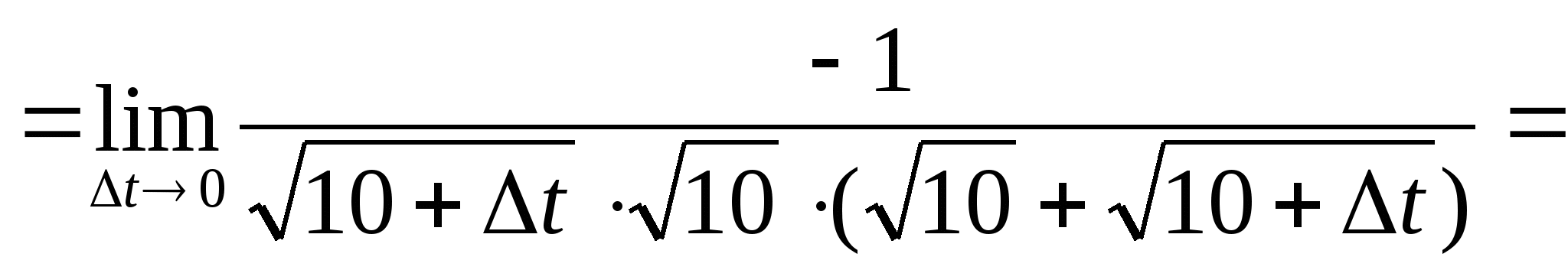
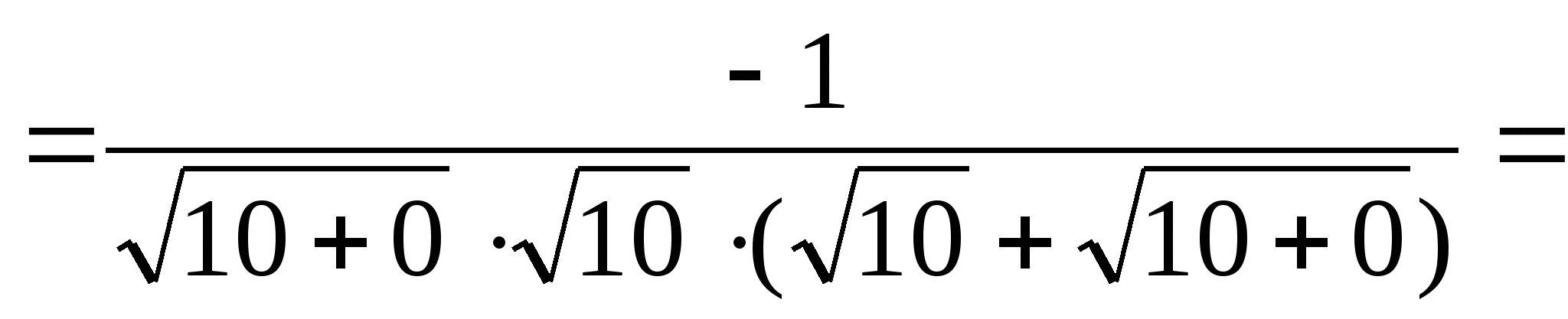
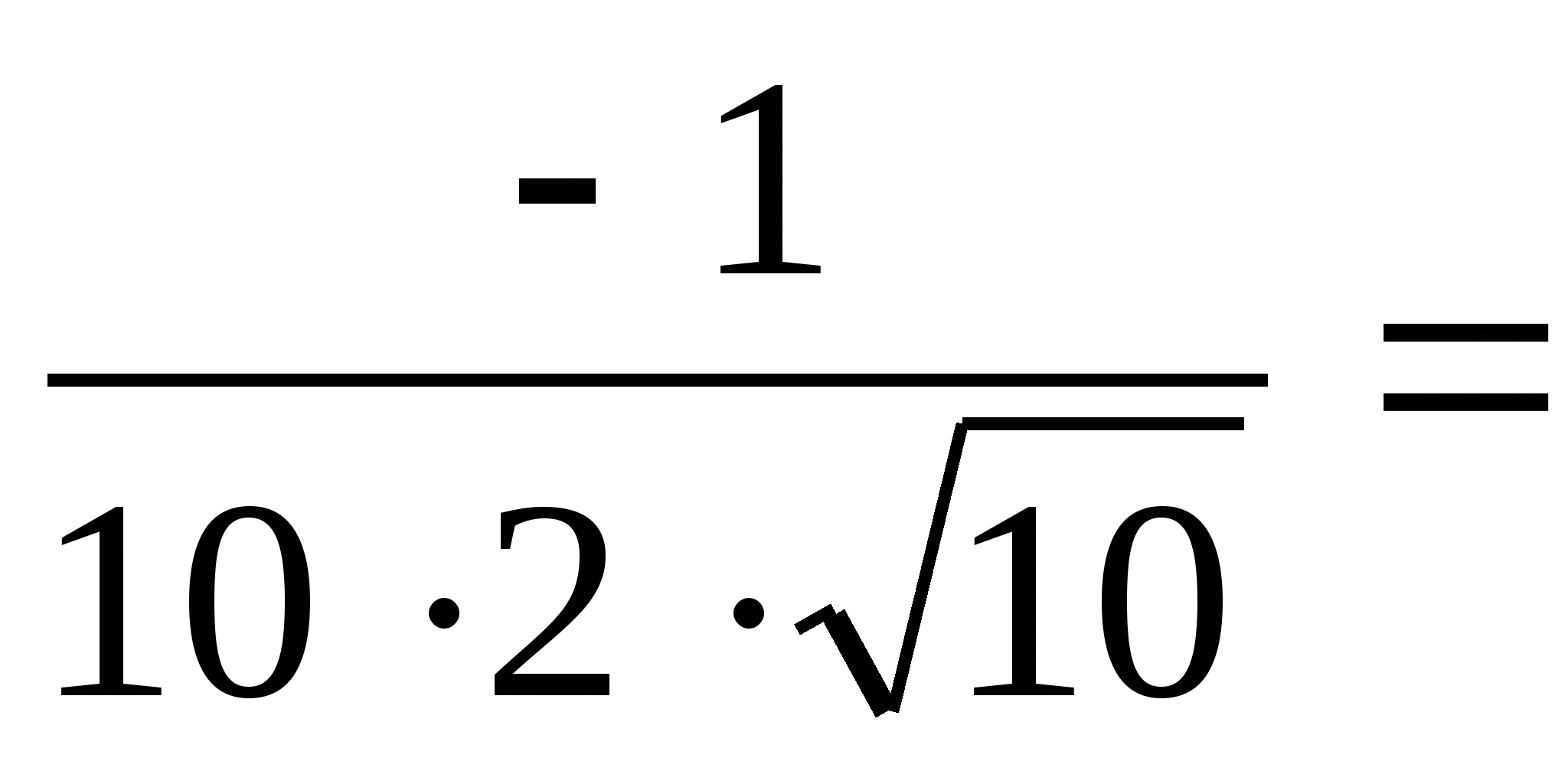
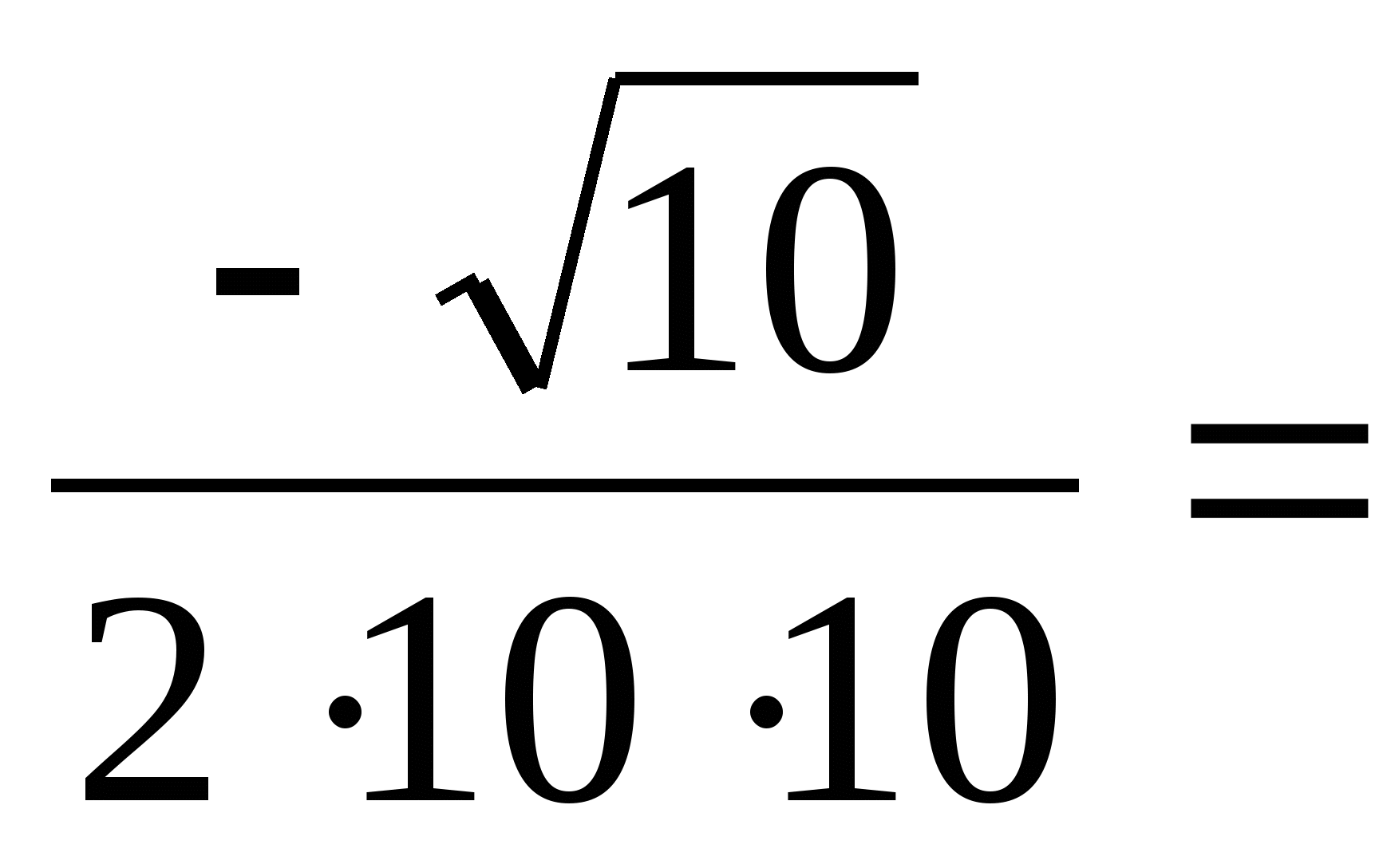
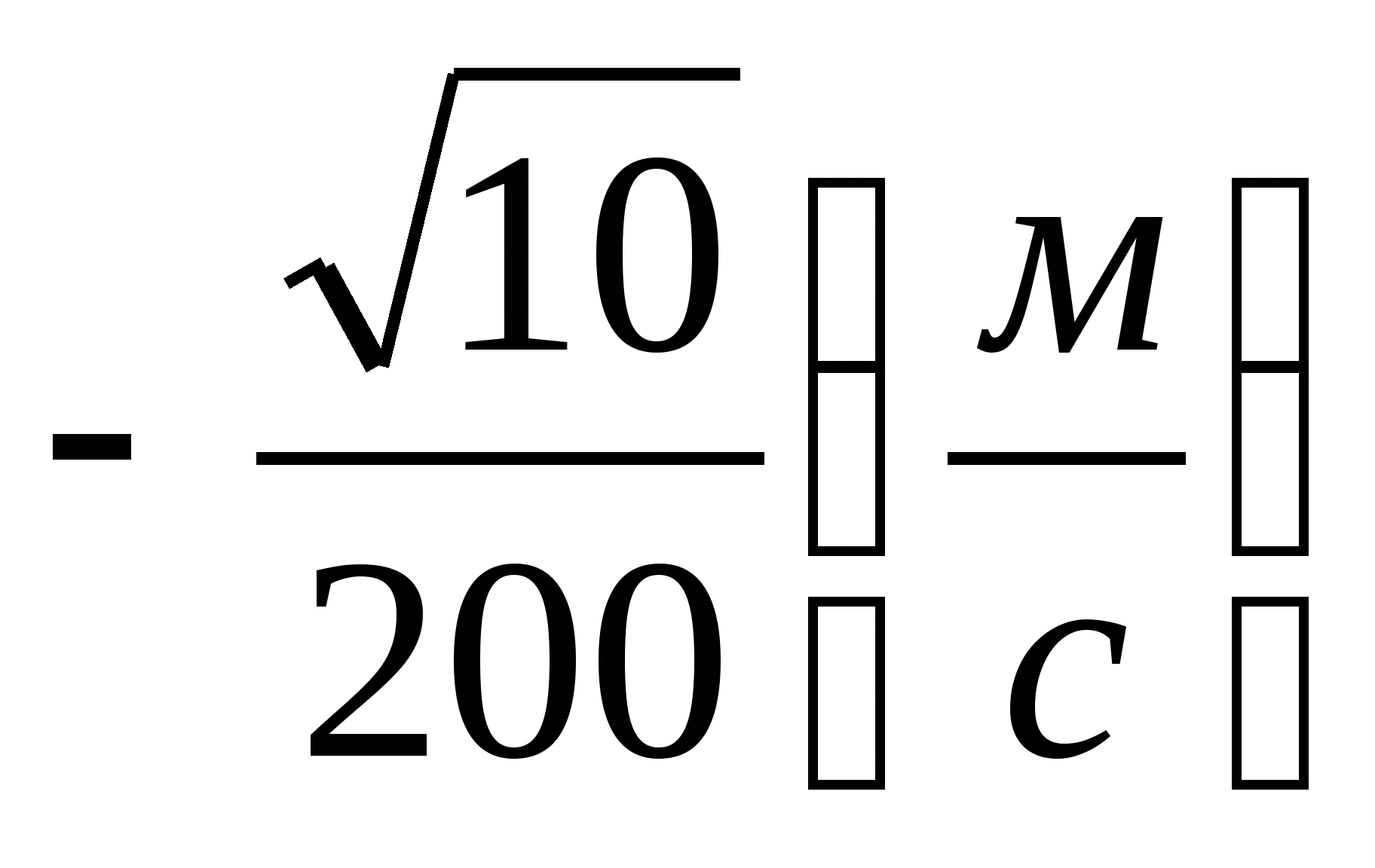ІІ. Актуалізація опорних знань.

Фронтальне опитування:

1.Дайте означення границі функції в точці.

2. Дайте означення функції неперервної на проміжку?

3. Сформулюйте властивості границі функції.

4. Сформулюйте означення дотичної до кола.

5.Запишіть рівняння прямої.

6.Що таке кутовий коефіцієнт прямої? Чому дорівнює кутовий коефіцієнт прямої:

а) яка є бісектрисою І і ІІІ координатних кутів;

б) яка є бісектрисою ІІ і ІV координатних кутів;

в) паралельна осі абсцис?

ІІІ. Мотивація навчальної діяльності на уроці повідомлення теми мети уроку

ІV.Вивчення нового матеріалу.

План вивчення теми

1. Означення похідної функції в точці х_{о .}

2. Яка функція називається диференційованою в точці? на проміжку?

3. Схема знаходження похідної функції f(x) за означенням .

4. Використання означення під час обґрунтування формул для обчислення похідних деяких функцій.

5. Зв'язок між диференційованістю та неперервністю функцій.

6. Геометричний зміст похідної. Кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці

7. Фізичний зміст похідної. Швидкість та прискорення прямолінійного руху.

Пояснення нового матеріалу: Конспект учня.f(x)неперервна в точці х_о при х0 f0

Функцію, яка має похідну в точці х_о, називають диферен­ційованою в цій точці.

Функцію, яка має похідну в кожній точці деякого проміжку, називають диференційованою на цьому проміжку. Операція знаходження похідної називається диференціюванням

Для знаходження похідної функції у=f(x) за означенням можна користуватися схемою

1 . Знайти приріст функції який відповідає приросту аргумента

2.Знайти відношення

3. Зясувати ,до якої границі прямує відношенняприх0. Це і буде похідна.

Сприймання і усвідомлення геометричного змісту похідної, рівняння дотичної.

Н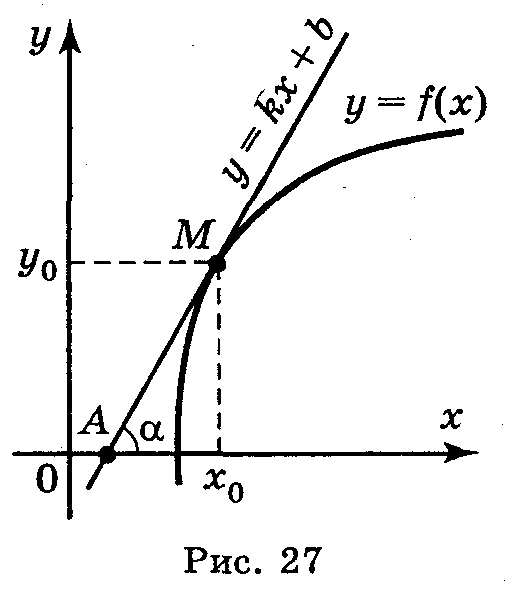а попередньому уроці ми розглядали задачу про знаходжен­ня кутового коефіцієнта дотичної. Порівнюючи одержані резуль­тати з означенням похідної, можна зробити висновок: значення похідної функції у = f(x) в точці x_o до­рівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x_o : f'(x_o) = k = tg α (рис. 27)

Розглянемо функцію у = f(x). Її гра­фік зображено на рис. 27.

У точці М(x_o;y_o) проведено дотичну до кривої у=f(x). Складемо рівняння дотичної AM, знаючи координати точки М(x_o;y_o) дотику і рівняння у = f(x) кри­вої. Дотична - це пряма. Рівняння будь-якої прямої має вигляд:

у = kx + b. Оскільки k = f'(x_o), тому рівняння дотичної має вигляд:

у = f'(x_o)x + b.

(1)

Знайдемо b, виходячи з того, що дотична проходить через точку М(x_o;y_o) і тому її координати задовольняють рівнянню дотичної:

у_о = f '(х_o) · х_o + b, звідси b = у_o - f '(x_o) · x_o.

Тепер підставимо значення b в рівняння (1) дотичної і одер­жимо:

у = f '(x_o) ·x + у_о - f '(x_o) · x_o y - y_о = f '(x_о )(x - x_o)·

Отже, рівняння дотичної до кривої у = f(x) в точці М(x_o; у_o) має вигляд:

y - y_о = f '(x_o)(x - x_o).

(2)

Рівняння дотичної до кривої у = f(x) у заданій точці x_o можна знаходити за таким планом (схемою):

1. Записуємо рівняння дотичної: y - y_о = f '(x_o)(x - x_o).

2. Знаходимо у_o = f(x_o)·

3. Знаходимо значення f '(x) у точці x_o: f '(x_o).

4. Підставляємо значення x_o, y_o і f '(x_o) y рівняння y - y_о = f '(x_o)(x - x_o). .

Сприймання і усвідомлення механічного змісту похідної.

На попередньому уроці ми розглядали задачу про знаходження миттєвої швидкості прямолінійного руху матеріальної точки. Порівнюючи одержані результати з означенням похідної, можна зробити висновок: якщо матеріальна точка рухається прямо­лінійно і її координата змінюється по закону s = s(t), то швидкість її руху v(t) в момент часу t дорівнює похідній s'(t):

v(t) = s'(t).

V. Формування вмінь та навичок при розв'язуванні задач по вивченому матеріалу.

Приклад 1. Знайдіть похідну функції f(x) = Зх² + 2 в точці х_о.

Розв'язання

Знайдемо приріст функції:

Δf = f(х_о + Δx) - f(x_o) = 3(х_о + Δx)² + 2 - 3 - 2 =

= 3 + бх_оΔx+ 3Δx² + 2 - 3 - 2 = 6х_оΔх+ 3Δx² = Δx(6x_ο + 3Δx).

Знайдемо відношення приросту функції до приросту аргументу:

.

Знайдемо похідну даної функції в точці х₀:

f '(х_o) = = = 6х_о + 3 · 0 = 6х_о.

Відповідь: 6х_о.

Приклад 2. Знайдіть похідну функції f(x) = kx + b (k і b постійні) у точці x_o.

Розв'язання

Знайдемо приріст функції:

Δf = f(х_о + Δx) - f(x_o) = k(x_o + Δx) + b - kx_o - b = kx_o + kΔx - kx_o = kΔx.

Знайдемо відношення приросту функції до приросту аргументу:

Отже, f '(х_o) = = = k, або (kx + b)' = k.

Відповідь: k.

Приклад 3. Розглянемо функцію у == хⁿ, де n N.

Знайдемо похідну цієї функції, для цього зафіксуємо значення аргументу х. і надамо йому приросту x, тоді:

1) y = (x_o+x)ⁿ - ,

2)

… + .

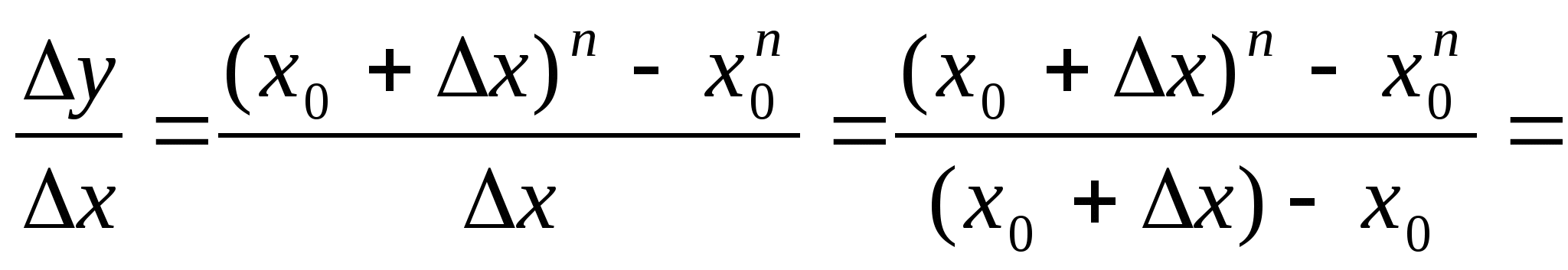
(Скористалися фор­мулою

.

3) f'(x_o) + ++…+.

Звідси (xⁿ)' =nx^{n - 1}, де n N .

а) Розв'язування задач:

№ 1. Користуючись означенням похідної, знайдіть похідну функ­ції f, якщо:

а) f(x) = х² + 1 в точці 1; б) f(x) = х³ в точці 1;

в) f(x) = в точці 1; г) f(x) = в точці 1.

Відповідь: а) 2; б) 3; в) -1; г) .

№ 2. Користуючись означенням похідної, знайдіть f'(x), якщо:

a) f(x) = 2х + 3; б) f(x) = х² + х;

в) f(x) = 5х² + 6х; г) f(x) = 3х² + 5х + 6.

Відповідь: а) 2; б) 2х + 1; в) 10х + 6; г) 6х + 5.

№ 3. За допомогою формули (kx + b)' = k, знайдіть похідні функції:

a) f(x) = 3х + 4; б) f(x) = 6х - 1;

в) f(x) = 10; г) f(x) = 5х.

Відповідь: а) 3; б) 6; в) 0; г) 5.

№ 4. Точка рухається по закону s(t) = 1 + 2t² (м). Знайдіть швид­кість руху точки в момент часу t = 1 с.

Відповідь: 4 .

№ 5. Знайдіть миттєву швидкість руху точки, якщо:

a) s(t) = 3t + 1; б) s(t) = 3 - 2t; в) s(t)=t²·, г)s(t) = 3t².

Відповідь: а) 3; б) -2; в) 5t; г) 6t.

№6. Точка рухається прямолінійно за законом s(t) = 2t³ - 3t (s - шлях в метрах, t - час в секундах). Обчисліть швидкість руху точки:

а) в момент часу t; б) в момент t = 2 с.

Відповідь: а) (6t² - 3); б) 21.

№7. Рух точки відбувається за законом s(t) = t² - 4t + 6. У який момент часу швидкість руху дорівнює: а) 0; б) 10?

Відповідь: а) t = 2; б) t = 7.

№8. Складіть рівняння дотичної до графіка функції у = х² - 4х в точці x_o = 1. Виконайте схематичний рисунок.

Розв'язання

1. y - y_о = f '(x_o)(x - x_o) - рівняння шуканої дотичної.

2. у_o= 1² - 4·1 = 1 - 4 = - 3.

3. .

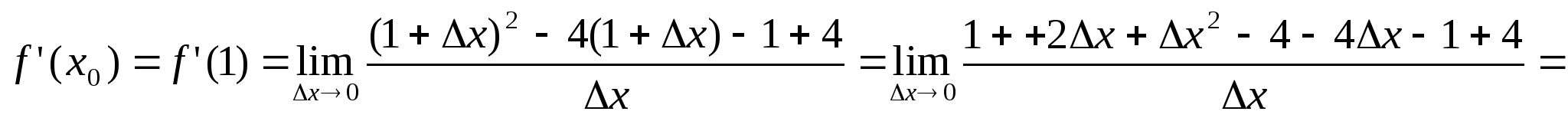
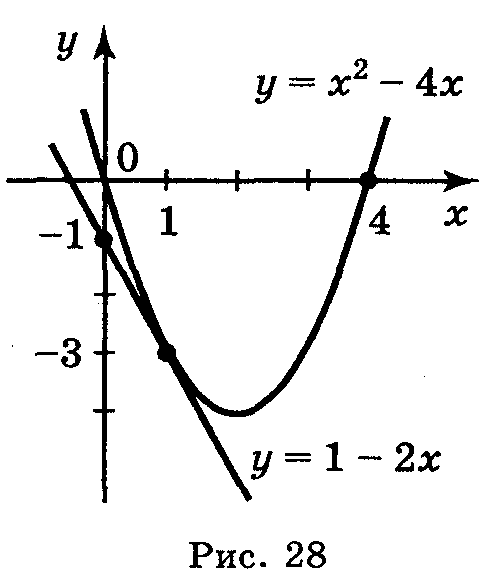
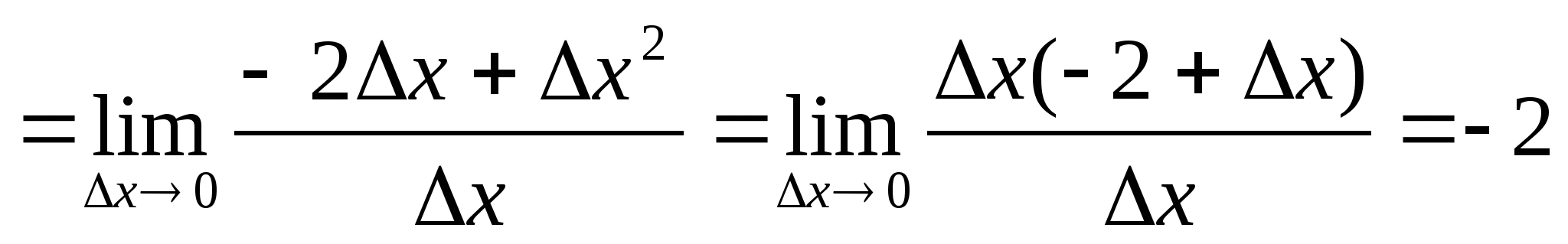4. Підставляємо значення x_o = 1, y_o = -3, f'(x_o) = -2 у рівняння дотичної: y + 3 = -2(x - 1), або у = - 3 - 2x + 2, або y = -1 - 2х (рис. 28).

№ 9. Який кут (гострий чи тупий) утворює з додатним напрямом осі ОХ дотична до графіка функції: а) у = х² + 2х в точці x = 1; б) у = х² + 2х в точці x = -27

Відповідь: а) гострий; б) тупий.

№ 10. Запишіть рівняння дотичної до параболи у = 3х² - 2 у точці:

а) x_o = -2; б) x_o = 0; в) x_o = 1.

Відповіді: а) у = - 12х - 14; б) у = -2; в) у = 6х - 5.

Історична довідка

Знак Δх запровадив 1755 року Л.Ейлер. Цей знак утворено з грецької букви « дельта», оскільки латиною слово differentia - різниця , відмінність,починається з букви d.

Термін « похідна» (французьке derive`e) увів 1797 року французький математик Ж.Лагранж (1736-1813). Він запровадив символ f ^І(x). Інакше позначення для похідної dx запропонував в 1675 році Г.Лейбніц, якого справедливо вважають творцем сучасної символіки математичного

аналізу

VІ. Підведення підсумків уроку.

а) Дайте відповіді на запитання

1. Що називається похідною функції в точці х_{о .}

2.Яка функція називається диференційованою в точці? на проміжку?

3.Схема знаходження похідної функції f(x) за означенням .

4.Геометричний зміст похідної. Кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці

5.Фізичний зміст похідної. Швидкість та прискорення прямолінійного руху.

б)Коментування діяльності учнів на уроці, виставляння оцінок

VІІ. Домашнє завдання.

Розділ 2. п.7 вивчити конспект

Самостійна робота с.77