- Учителю
- Конспект урока по теме:Решение тригонометрических уравнений. Отбор корней по заданным условиям.
Конспект урока по теме:Решение тригонометрических уравнений. Отбор корней по заданным условиям.
Тема: Решение тригонометрических уравнений.
Отбор корней по заданным условиям.
Цели урока:
-
Образовательные - обеспечить повторение, обобщение и систематизацию материала темы.
-
Развивающие - способствовать формированию умений применять приемы отбора корней при решении тригонометрических уравнений.
-
Воспитательные - содействовать воспитанию интереса к математике и ее приложениям, активности, общей культуры.
Тип урока: урок обобщения и систематизации знаний.
План урока.
-
Оргмомент.
-
Самостоятельная работа.
-
Решение тригонометрических уравнений. Отбор корней по заданным условиям.
-
Выполнение упражнений.
-
Итоги урока.
-
Домашнее задание.
-
Организационный момент
На сегодняшнем уроке мы будем отрабатывать способы отбора корней при заданных условиях используя тригонометрические неравенства.
-
Самостоятельная работа.
Вариант 1
-
Найдите все решения уравнения cos 2x + sin2x +
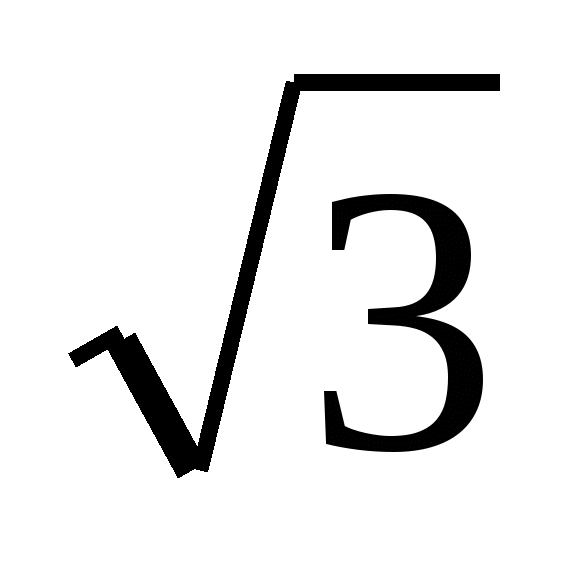 cos x = 0, принадлежащие отрезку [-; ];
cos x = 0, принадлежащие отрезку [-; ];
-
Решите уравнение cos2x + 6sin x - 6 = 0
Ответы:
-
cos 2x + sin2x +
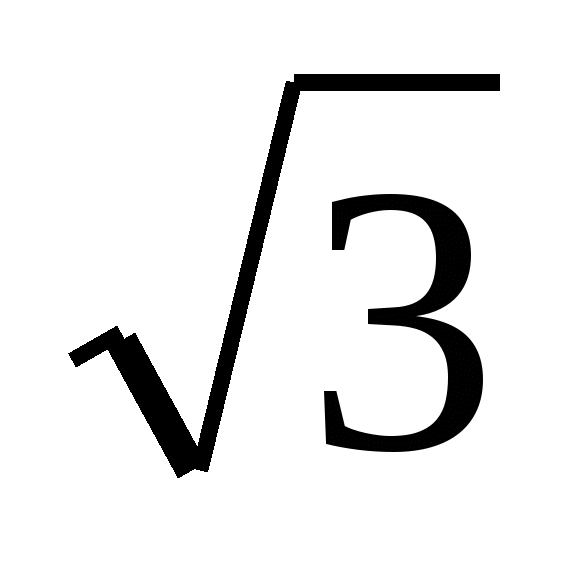 cos x = 0; cos2x - sin2x +
sin2x +
cos x = 0; cos2x - sin2x +
sin2x + 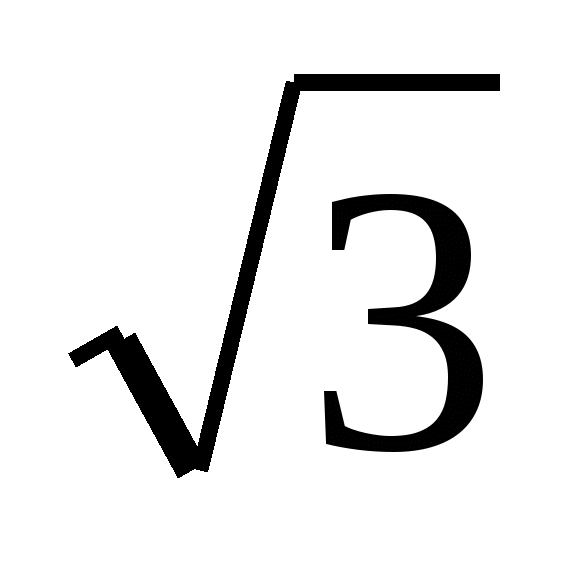 cos x = 0;
cos x = 0;
cos x (cos x + ![]() ) = 0; cos x = 0 (поскольку cos x +
) = 0; cos x = 0 (поскольку cos x + ![]() 0). Промежутку [-; ] принадлежат два решения два решения этого
уравнения:
0). Промежутку [-; ] принадлежат два решения два решения этого
уравнения: ![]() и
и ![]() .
.
Ответ: ![]() ;
; ![]() .
.
-
cos2x + 6sin x - 6 = 0; 1 - sin2x + 6sin x - 6 = 0; sin2x 6sin x + 5 = 0; sin x = t; t2 - 6t + 5 = 0; t1 = 5; t2 = 1.
sin x = 5 корней нет;
sin x = 1; x = ![]() + 2k, kZ.
+ 2k, kZ.
Ответ: x = ![]() + 2k, kZ.
+ 2k, kZ.
Вариант 2
-
Найдите все решения уравнения
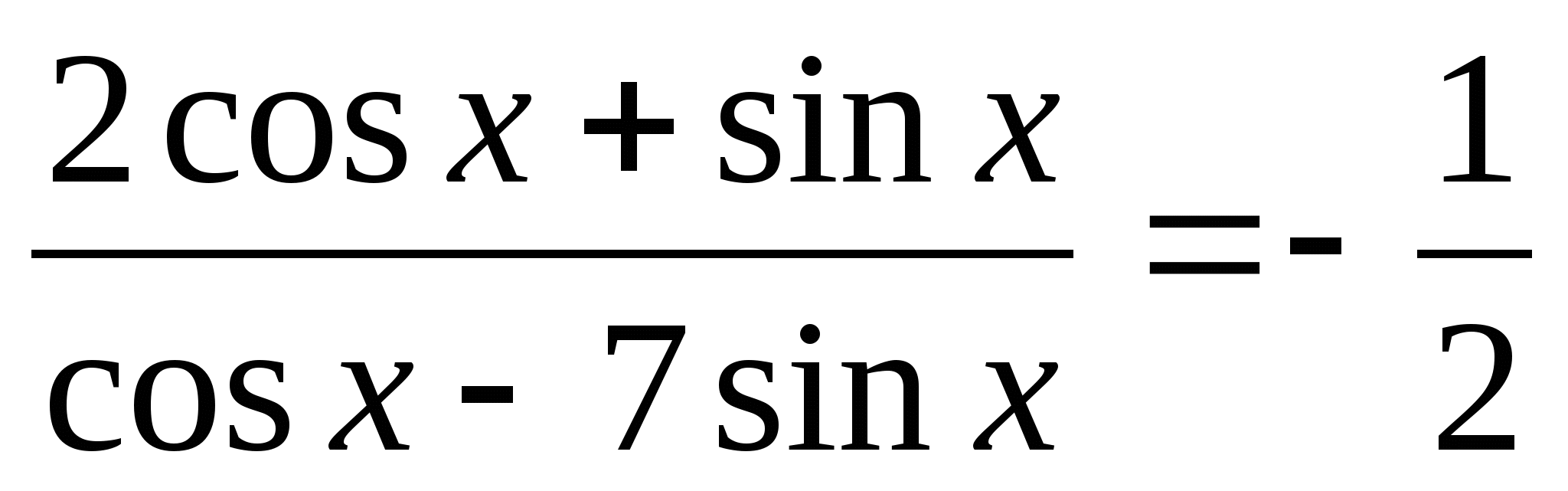 , принадлежащих промежутку [-; ];
, принадлежащих промежутку [-; ];
-
Решите уравнение cos 2x + 8sin x = 3.
Ответы:
-
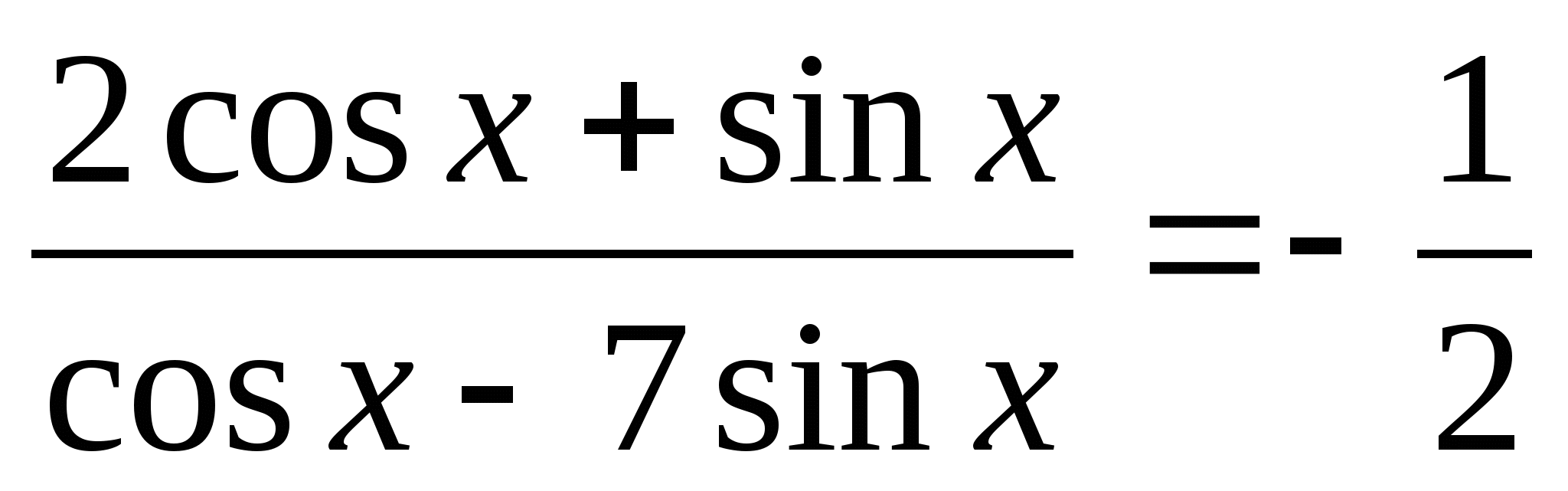
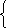 ;
4cos x + 2sin x = cos x + 7sin x
;
4cos x + 2sin x = cos x + 7sin x
cos x - 7sin x 0
5cos x = 5sin x; cos x = sin x.
Нули косинуса не являются корнями последнего уравнения, значит, его можно разделить на cos x:
tg x = 1; x = ![]() , nZ.
, nZ.
При этих значениях cos x - 7sin x 0.
Промежутку [-; ] принадлежат корни ![]() и
и ![]() ;
;
Ответ: ![]() ;
; ![]() .
.
3. Решение тригонометрических уравнений. Отбор корней по заданным условиям.
Сегодня на уроке мы рассмотрим еще несколько решений тригонометрических уравнений с отбором корней по заданным условиям.
Пример №1.
Найти все корни уравнения (1 + tg2x)·sin x - tg 2x + 1 = 0, удовлетворяющее неравенству tg x 0.
Р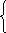 ешение:
(1 +
ешение:
(1 + ![]() ) sin x
) sin x ![]()
![]() +1 = 0
+1 = 0
tg x 0


 sin
x tg x
sin
x tg x
В приведенном решении одним из элементов
обоснования является тригонометрический круг,
на котором изображены множества решений
 0
уравнений и неравенства системы и из которого
0
уравнений и неравенства системы и из которого
сразу видно, как образуется пересечение этих
множеств. Однако в случае необходимости
последнюю систему можно решить и
аналитически следующим образом (заметим, что тригонометрический круг при этом помогает хотя бы выработать гипотезу о принципе отбора корней).
Р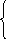 ассмотрим
три случая:
ассмотрим
три случая:
-
sin x = 1, решений нет, ибо если sin x = 1 то cos2x = 1 - sin2x = 0, и
tg x не существует;
tg x 0
-
x

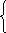 =
= 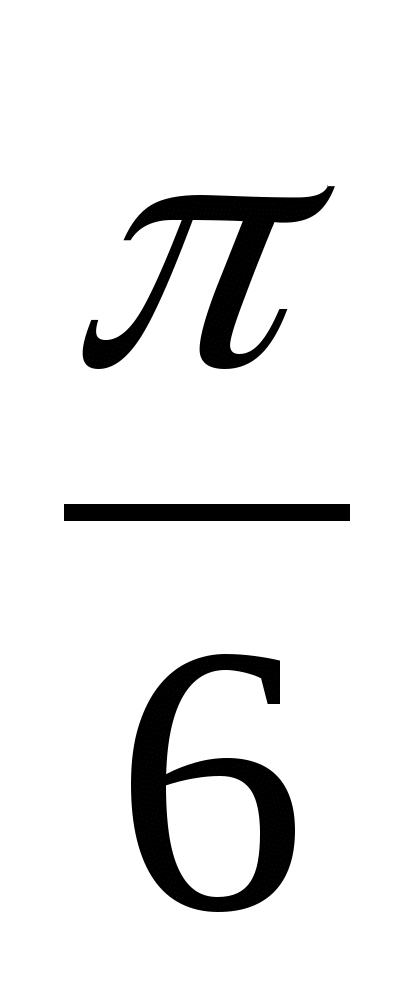 + 2n, nZ; x =
+ 2n, nZ; x = 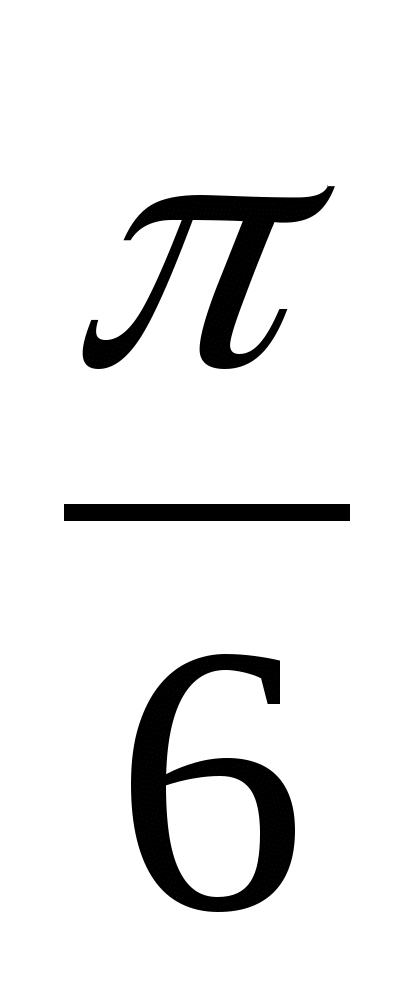 + 2n, nZ
+ 2n, nZ
tg x 0
так как tg ![]() =tg
=tg![]()
0;
0;
-
x
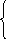 =
= 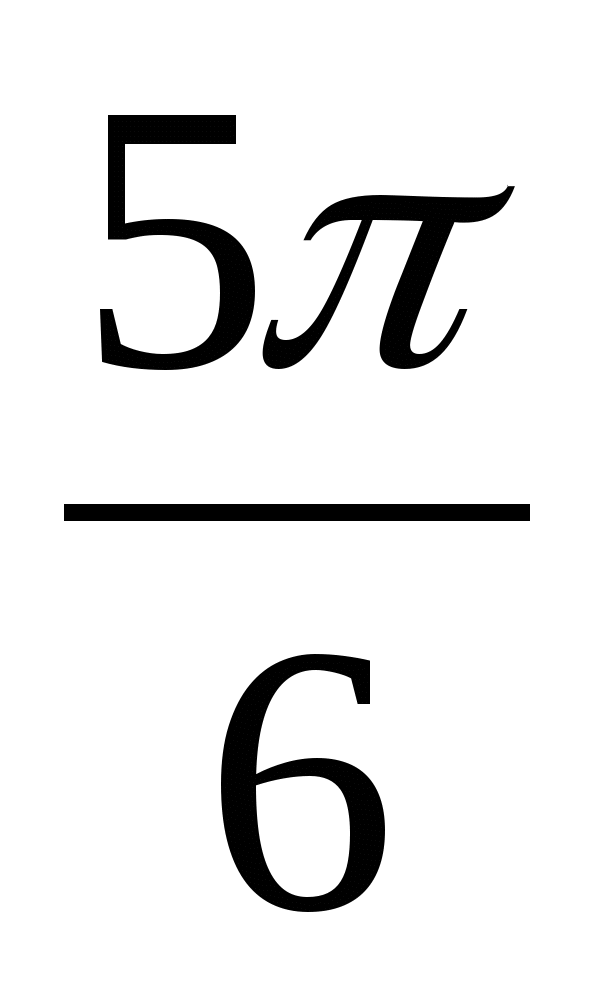 + 2m, mZ; решений нет, так как
+ 2m, mZ; решений нет, так как
tg x 0 tg![]() =tg
=tg![]()
0.
0.
Ответ:![]() .
.
Пример №2.
Решить уравнение 2sin (3x +![]() )
=
)
= ![]() .
.
Р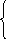
 ешение:
4sin2(3x +
ешение:
4sin2(3x + ![]() ) = 1 + 8sin 2x cos22x,
) = 1 + 8sin 2x cos22x,
2sin (3x + ![]() ) 0
) 0

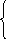
 2
- 2cos (6x +
2
- 2cos (6x + ![]() ) = 1 + 4sin 4x cos 2x,
) = 1 + 4sin 4x cos 2x,
sin (3x + ![]() ) 0
) 0

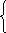

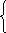 1
+ 2sin 6x = 2(sin 6x + sin 2x), sin 2x =
1
+ 2sin 6x = 2(sin 6x + sin 2x), sin 2x = ![]() ,
,
sin(3x + ![]() ) 0 sin(3x +
) 0 sin(3x + ![]() ) 0.
) 0.
Рассмотрим два случая:
1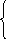
 )
x =
)
x = ![]() + n, nZ; x =
+ n, nZ; x = ![]() + n, n =0, 2, 4,…,
+ n, n =0, 2, 4,…,
sin![]()
0
0
так как sin ![]() = sin
= sin ![]() = (1)n;
= (1)n;
-
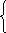
 x
=
x
= 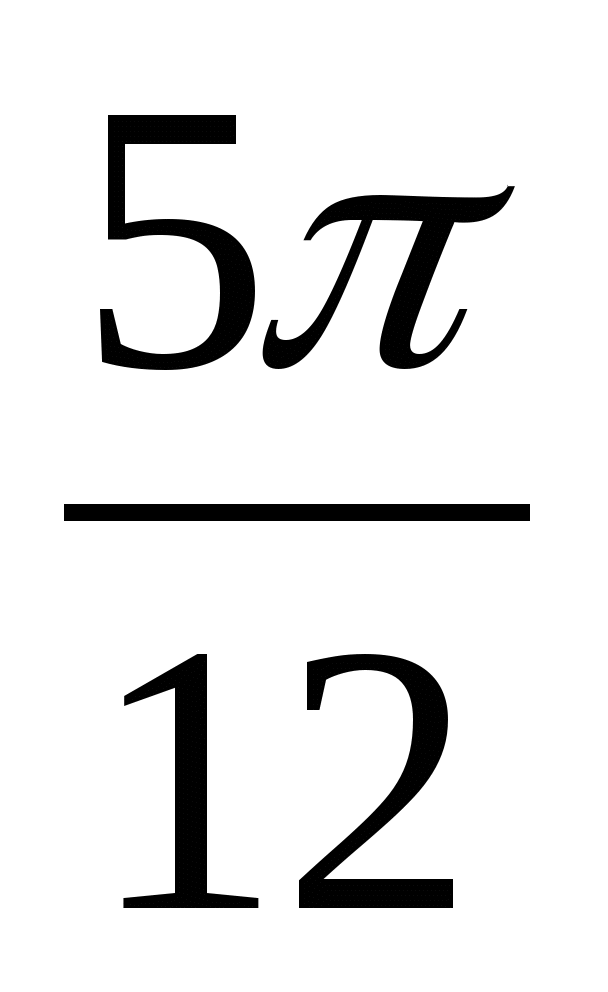 + m, mZ; x =
+ m, mZ; x = 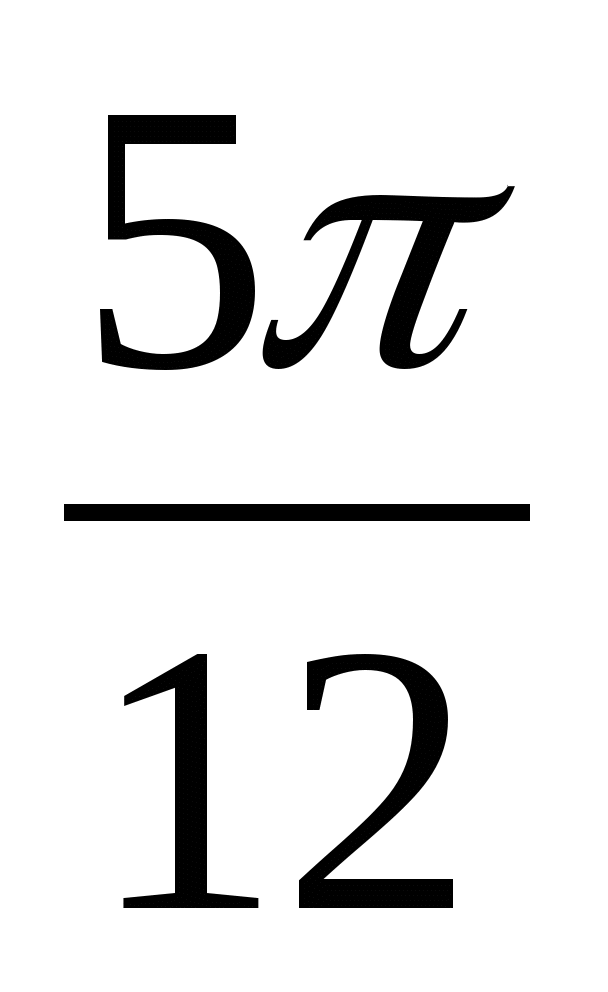 + m, m = 1, 3, …,
+ m, m = 1, 3, …,
sin ![]() 0
0
так как sin![]() = sin
= sin ![]() = (1)m+1.
= (1)m+1.
Ответ: ![]() + n,
+ n, ![]() + (2m + 1), n,mZ.
+ (2m + 1), n,mZ.
-
Выполнение упражнений
-
Решите уравнение
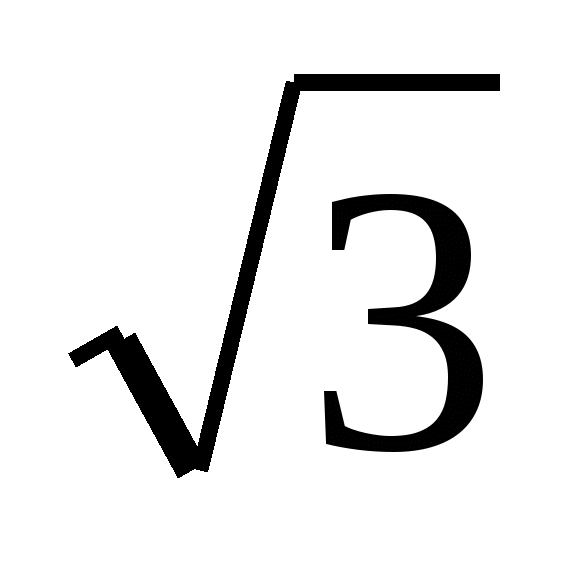 sin x = cos x
sin x = cos x
Решение: ![]() sin x = cos x
sin x = cos x
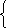
3sin2x = cos2x
sin x 0
3sin2x = 1 - sin2x; 4sin2x = 1;
учитывая неравенство sin x 0, получаем sin x = ![]() ;
;
x = (1)n ·![]() + n, nZ;
+ n, nZ;
Ответ: (1)n ·![]() + n, nZ;
+ n, nZ;
-
Найти решение уравнения cos 4x = 2cos2( x), принадлежащее
[ 0; ![]() ].
].
Решение: cos 4x = 2cos2( x);
2cos22x - 1 + 2cos2x = 0;
2cos22x + (2cos2x - 1) = 0;
2cos22x + cos 2x = 0;
cos 2x (2cos 2x + 1) =0;
cos 2x = 0 или 2cos 2x + 1 = 0;
x = ![]() +
+ ![]() , nZ; x =
, nZ; x = ![]() + k, kZ;
+ k, kZ;
при n = 0; x1 = ![]() принадлежит отрезку [0;
принадлежит отрезку [0; ![]() ].
].
-
Итоги урока
Несколько уроков мы с вами повторяли решение тригонометрических уравнений и отрабатывали умение отбирать корни уравнения по заданным условиям. Учились избегать неприятностей в ответах надеюсь нам это удалось.
6. Домашнее задание