Урок алгебры в 7 классе «Свойства степени с натуральным показателем»»

Конспект урока по алгебре

«Свойства степени с натуральным показателем»

Автор:

Гордеева Марина Эвальдовна

учитель математики МКОУ Нижнечирской ООШ

г. Волгоград

2014 год.

Предмет - алгебра 7 класс (урок алгебры)

Учебно-методическое обеспечение:

1. Алгебра 7 класс. Автор: Дорофеев Г.В. и др. Москва, «Просвещение» 2010г.

2. Дидактические материалы Алгебра 7, авторы Евстафьева, А.П., Карп. М., «Просвещение», 2011г.

3. Контрольные работы Алгебра 7-9, авторы Кузнецова Л.В., Минаева С.С. и др. М., «Просвещение», 2011г.

Тип урока: урок обобщения и систематизации знаний.

Формы работы: фронтальная, групповая, парная, индивидуальная.

Продолжительность урока: 45 минут.

Методы обучения: словесный, наглядный, практический, проблемный.

Оборудование:

1. Компьютер.

2. Мультимедиапроектор

3. Экран.

4. Медиапродукт: Среда - Microsoft Office PowerPoint. (наглядная презентация учебного материала Приложение 1).

- 3 вида карточек с дифференцированными заданиями, карточка-консультант с формулами свойств степени, зачетный лист.

Цели урока

-познавательные: повторение, обобщение и систематизация знаний по теме «Степень натуральным показателем и ее свойства». Создание условий контроля (взаимоконтроля) усвоения знаний и умений. Обучение умению применять приемы обобщения, сравнения, выделения главного, переноса знаний в новую ситуацию, развития математического кругозора, мышления, речи, внимания и памяти.

- коммуникативные: способствовать формированию умений работать в парах, группах, развивать умение высказывать и отстаивать собственную точку зрения.

- регулятивные: развивать умение планировать свою работу, осуществлять задуманный план, подводить итоги работы, делать выводы. Развивать умение организовывать работу, умение взаимо- и самоконтроля своей деятельности, формировать положительный мотив учения, развивать умения, необходимые при учебно-познавательной деятельности

Этапы урока

1.Организационный момент. Постановка целей и задач урока. Выбор учащимися индивидуального образовательного пути на уроке. 1 путь: повторение, а затем самостоятельная работа, или

2 путь: сразу самостоятельная работа.

2.Актуализация, систематизация опорных знаний.

1. Всесторонняя проверка знаний.

2. Самостоятельная работа: работа в группах, взаимопроверка, самопроверка

3.Итоги урока, вывод.

4. Рефлексия.

5. Домашнее задание.

Ход урока

1.Организационный момент. (1-2 минуты)

Учитель

Предполагаемые ответы и действия учеников

Здравствуйте, дети! Садитесь. Запишите в тетрадях число, классная работа. Эпиграфом нашего урока будут слова, сказанные Цицероном: «Ошибаться может каждый, оставаться при своей ошибке - только безумный».

Как вы понимаете эти слова?

Каждый человек может ошибаться, каждый имеет право на ошибку, но при этом очень важно найти её, признать её и исправить!

2. Постановка целей, задач для 2 этапа урока и их реализация.( не более 5 минут)

Учитель

Предполагаемые ответы учеников

На доске

Скажите, какую тему мы изучали?

Степень. Свойства степени с натуральным показателем

Степень. Свойства степени с натуральным показателем

Что при изучении темы мы узнали?

Определение степени с натуральным показателем, свойства степени

Достаточно ли было времени для того, чтобы усвоить материал?

-Достаточно

-Нет.

Кто из вас готов презентовать свои знания?

Какую цель вы сейчас перед собой поставит?

-Мы

Как можно лучше написать проверочную работу.

Предлагаю вам выбрать задание для самостоятельной работы

1 вид каточек (обязательный уровень)

2 вид (повышенный уровень)

3 вид (высокий уровень)

Выбирают карточки и решают их, пишут через копирку.

(в презентации быть ответы)

*Предлагаемые задания даны в конце конспекта урока.

Учитель

Предполагаемые ответы

учеников

На доске

Чем будем заниматься на уроке с остальными?

Сначала повторим все свойства степени с натуральным показателем, затем проверим свои знания, подведем итоги, сделаем выводы.

Каким будет 1 этап урока

Повторение

Что нам необходимо сделать и зачем?

Открыть учебник, или тетрадь и повторить все свойства для того, чтобы ответить на вопросы и подготовиться к самостоятельной работе

Согласно вашему плану, приступаем к 1 этапу урока: повторение (актуализация).

Учитель

Предполагаемые ответы

учеников

На доске

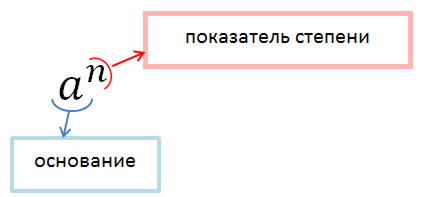
Что такое степень числа с натуральным показателем?

Отвечают на вопросы учителя:

Степенью числа a с натуральным показателем n большим 1, называют произведение n множителей, каждый из которых равен а.

aⁿ⁼ а а а а…. - n раз

Например: 4 • 4 • 4 • 4 • 4 • 4 = 4⁶

Как определить знак результата при возведении в степень?

Отрицательное число, возведённое в чётную степень, есть число положительное.

Отрицательное число, возведённое в нечётную степень, - число отрицательное.

Квадрат любого числа есть положительное число или нуль (неотрицательное число), то есть: a² ≥ 0 при любом a.

=9 положительное число 0

= - 3 отрицательное число

=49 положительное число 0

=49 положительное число 0

=0

Чему равна первая степень любого числа

Первая степень любого числа равна самому числу.

a¹ = a

= - 3

= 3

Чему равна нулевая степень любого числа

Нулевая степень любого числа равна 1.

а^{0 =} 1

(-32)⁰ = 1

Как записывается отрицательная степень числа

Отрицательная степень числа записывается в виде дроби, где числитель равен 1, а знаменатель равен данной степени, но с положительным основанием:

a^n=1/ aⁿ

=

Как выполняется умножение степеней с одинаковым основанием?

При умножении степеней с одинаковыми основаниями показатели степеней складывают:

aⁿ·a^k=a^n+k

b • b² • b³ • b⁴ • b⁵ = b ^{1 + 2 + 3 + 4 + 5} = b¹⁵

Как выполняется деление степеней с одинаковым основанием?

При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.

aⁿ : a^k=a^{n - k}

(2b)⁵ : (2b)³ = (2b)^{5 - 3} = (2b)²=4b²

Как возводят степень в степень?

При возведении степени в степень, показатели степеней перемножают/

(aⁿ)^к = a^nk

(a⁴)⁶ = a^{4 • 6} = a²⁴

Как возводят в степень произведение?

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

(ав)ⁿ⁼ aⁿ вⁿ

(6 • a² • b³ • c )² = 6² • a^{2 • 2} • b^{3 • 2} • с ^{1 • 2} = 36 a⁴ • b⁶ • с ²

Учитель

Предполагаемые ответы

учеников

На доске

Как возводят в степень дробь?

При возведении в степень дроби возводят в эту степень отдельно её числитель и знаменатель.

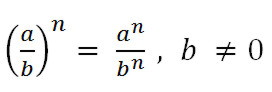
(5 : 3)¹² = 5¹² : 3¹²

Порядок действий в примерах

В выражениях со степенями, не содержащими скобки, сначала выполняют возведение в степень, затем умножение и деление, а в конце сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

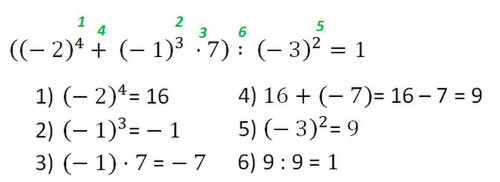
3. Постановка целей и задач, их реализация для 3 этапа урока. ( не более 25-30 минут)

Учитель

Предполагаемые ответы действия учеников

На доске

Мы повторили, обобщили, привели в систему ранее изученный материал по теме степень с натуральным показателем.

Что будем делать теперь?

Проверим свои знания, напишем самостоятельную работу.

Предлагаю, взять задания на выбор. Каждому из вас будет дана карточка, содержащая задания 3-х уровней сложности. В 1 столбике карточки задания на обязательный уровень знаний по данной теме. Во 2 столбике карточки задания на повышенный уровень сложности. В 3 столбике карточки задания на продвинутый уровень сложности. Выбирайте, решайте, успехов вам.

Выбирают карточки, решают их, при этом, садятся так, чтобы в одной группе были карточки одного и того же цвета.

• При затруднениях можно предложить карточки-консультанты, но при этом оценка будет снижена.

4. Подведение итогов работы 1 группы, выполнявшей самостоятельную работу с начала урока.

(не более 3 минут).

Учитель

Предполагаемые ответы и действия учеников

Что делаем теперь?

Для этого сдайте мне листы, на которых вы писали.

Как будем проверять работы?

Проверим решение самостоятельной работы.

Сдают листы с работами, оставляя себе тетради, на которых писали через копирку.

Обменяемся тетрадями и сделаем взаимопроверку, или сами проверим свои тетради.

Проверяют, исправляют ошибки, ставят оценки.

Обсуждение результатов работы

По желанию говорят о том, какие ошибки допустили, почему, делают для себя выводы о том, что необходимо еще раз повторить, чтобы на контрольной работе не сделать ошибок, или свести количество ошибок к минимуму.

5. Подведение итогов работы групп, выполнявших самостоятельную работу после

этапа повторения. ( не более 3 минут).

Учитель

Предполагаемые ответы и действия учеников

Что делаем теперь?

Для этого отдайте свои тетради, в которых вы писали ученикам 1 группы, которая уже выполнила проверку своей самостоятельной работы.

А что будете делать вы?

1 группа: проверим решение самостоятельной работы. Проверяют, исправляют ошибки, ставят оценки.

Остальные: посмотрим на процесс решения самостоятельной работы.

Рассматривают и объясняют решение каждого примера.

Обсуждение результатов работы

Проверяющие на доске выписывают ошибки, показывают правильное решение. Остальные делают для себя выводы о том, что необходимо еще раз повторить, чтобы на контрольной работе не сделать ошибок, или свести количество ошибок к минимуму.

Обязательно говорят о том, какое новое знание открыли для себя на уроке.

Вернемся к началу урока. Вспомним слова, сказанные Цицероном: «Ошибаться может каждый, оставаться при своей ошибке - только безумный».

Как эти слова проявили себя на сегодняшнем уроке?

Именно так и произошло, мы ошибались, но признавали свои ошибки, исправляли их и постараемся не допустить их на контрольной работе.

5. Домашнее задание.

1. Творческое. Оформите плакат «Степень и ее свойства».

2.Разноуровневые карточки. (прилагаются)

6. Подвести итоги урока поможет зачетный лист.

Зачетный лист

Фамилия Имя

оценка ученика

Оценка учителя

1.Теоретическая часть

2. Практическая часть

Итоговая оценка:

Эмоциональная оценка

О себе

Об уроке

Удовлетворен

Неудовлетворен

На что мне нужно обратить внимание при подготовке к зачету

Самостоятельная работа.

Критерии оценки самостоятельной работы:

Оценка

зачтено

«4»

«5»

Обязательная часть

9 заданий

9 заданий

9 заданий

Дополнительная часть

------------------

1 задание

2 задания

Обязательный уровень

Продвинутый уровень

Высокий уровень

Выполните действия №1-№5

Выполните действия №1- №5

Выполните действия №1- №5

№1.

С⁵∙С³

№1.

х¹¹∙х∙х²

№1.

х¹¹∙х∙х²∙х⁴у⁶∙х³у⁷

№2.

С⁸: С⁶

№2.

С⁸: С⁶:С

№2.

:С⁸: С⁶: С⁴

№3.

(С⁴)³

№3.

((С⁴)³) ³

№3.

(((С⁴)³) ³) ²

№4.

(К/В) ⁶

№4.

(К³/В⁸) ⁶

№4.

((К³/В⁸) ⁶) ²

№5.

(-2с³) ⁴

№5.

(-2 а⁴ в¹⁰с³) ⁴

№5.

(-2 а⁴ в¹⁰с³2х⁴ у⁹) ⁴

№6 - 9. Упростить выражение

№6-8. Упростить выражение

№6-8 .Упростить выражение

№6

№6

№6

∙

№7

(С⁴)³ ∙С

№7

(С⁴)³ ∙С∙ (С⁴)³

№7

((С⁴)³ ∙С∙ (С⁴)³)³

№8

2ху∙ 3x²у⁵

№8

-5а²с ∙ 2ас ∙ (-0,6с³)

№8 Вычислите:

-1∙ 3², (-1 ∙ 3)² 1∙(-3)², (2 ∙ 3) 1² ∙ (-3)²

№9 Сократите дробь

24 С⁵ х⁴

36 С³ х²

№9 Подбери множитель

(2а²в)²∙ ( ) = - 8а ⁹ в¹⁰

№9 Подбери множитель

(2а²в)²∙ ( ) = - 8а ⁹ в¹⁰

(2в³)² ∙ ( )²=100

№10 Сравните:

и ∙

№10 Сравните:

и ∙

№11При каком значении n выполняется равенство:

=10000

Карточка-консультант.

aⁿ·a^k=a^n+k

b • b² • b³ • b⁴ • b⁵ = b ^{1 + 2 + 3 + 4 + 5} = b¹⁵

При умножении степеней с одинаковыми основаниями показатели степеней складывают:

aⁿ : a^k=a^{n - k}

(2b)⁵ : (2b)³ = (2b)^{5 - 3} = (2b)²=4b²

При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.

(aⁿ)^к = a^nk

(a⁴)⁶ = a^{4 • 6} = a²⁴

При возведении степени в степень, показатели степеней перемножают/

(ав)ⁿ⁼ aⁿ вⁿ

(6 • a² • b³ • c )² = 6² • a^{2 • 2} • b^{3 • 2} • с ^{1 • 2} = 36 a⁴ • b⁶ • с ²

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

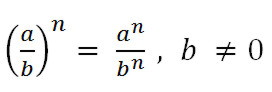
(5 : 3)¹² = 5¹² : 3¹²

При возведении в степень дроби возводят в эту степень отдельно её числитель и знаменатель.

=9 положительное число 0

= - 3 отрицательное число

=49 положительное число 0

=49 положительное число 0

=0

Отрицательное число, возведённое в чётную степень, есть число положительное.

Отрицательное число, возведённое в нечётную степень, - число отрицательное.

Квадрат любого числа есть положительное число или нуль (неотрицательное число), то есть: a² ≥ 0 при любом a.

a¹ = a

= - 3

= 3

Первая степень любого числа равна самому числу.

а^{0 =} 1

(-32)⁰ = 1

Нулевая степень любого числа равна 1.

a^n=1/ aⁿ

=

Отрицательная степень числа записывается в виде дроби, где числитель равен 1, а знаменатель равен данной степени, но с положительным основанием:

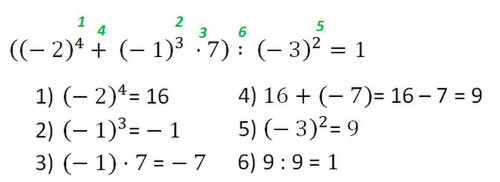
В выражениях со степенями, не содержащими скобки, сначала выполняют возведение в степень, затем умножение и деление, а в конце сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Оформление доски.

На доске

aⁿ⁼

Например: 4 • 4 • 4 • 4 • 4 • 4 =

= 0

= 0

= 0

= 0

=

a¹ = a

=

=

а^{0 =} 1

(-32)⁰ =

a^n=1/ aⁿ

=

aⁿ·a^k=

b • b² • b³ • b⁴ • b⁵ =

aⁿ : a^k=

(2b)⁵ : (2b)³ =

(aⁿ)^к =

(a⁴)⁶ =

(ав)ⁿ⁼

(6 • a² • b³ • c )² =

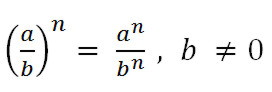
(5 : 3)¹² =
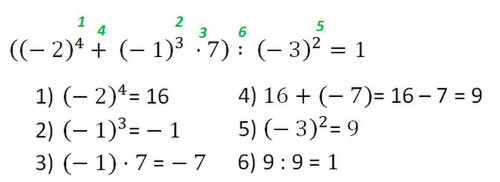