- Учителю
- Рабочая программа по алгебре и началам анализа 11 класс к учебнику Алимова Ш.А
Рабочая программа по алгебре и началам анализа 11 класс к учебнику Алимова Ш.А
муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная
школа № 42 с. Сандата
Согласовано Утверждено зам. директора по УВР приказом ______Н.В.Титаренко № 317 от 30.08. 2016г. « » ___________ 2016 г. Директор_______Е.Н.Фоменко
РАБОЧАЯ ПРОГРАММА
по__алгебре__и началам анализа
(учебный предмет, курс)
11 класс
на 2016-2017 учебный год
Учитель ___Сибирякова В.В.
РАССМОТРЕНО на заседании МО _учителей математики, информатики и физики
Протокол № 1 от 29.08 .2016г.
Руководитель МО ___________( КАЗАРЯН В.М.)
(подпись)
ПРИНЯТО на заседании Педагогического Совета Протокол № 1от «30» _августа_2016 г
с.Сандата 2016
-
Пояснительная записка
Рабочая программа по алгебре и началам анализа для 11 класса составлена на основании следующих нормативно- правовых документов:
-
1Федерального закона от 29.12.2012 года N273-ФЗ "Об образовании в Российской Федерации";
-
Приказа Министерства образования и науки Российской федерации от 05.03.2004 №1089"Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования"(в ред. приказов Минобрнауки России от 03.06.2008 №164, от 31.08.2009 №320, от 19.10.2009 №427, от 10.11.2011 №2643, от 24.01.2012 №39)
3.Приказа Минобразования России от 9 марта 2004 года № 1312 «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования»(в редакции приказов Минобрнауки России от 20.08.2008 №241, 30.08.2010 №889, 03.06.2011 №1994, 01.02.2012 №74);
4.Постановления Главного государственного санитарного врача Российской Федерации от 29 декабря 2010 г. N 189 г. Москва "Об утверждении СанПиН 2.4.2.2821-10 "Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (в редакции изменений №1, утверждённого Постановлением Главного государственного санитарного врача Российской Федерации от 29.06.2011 №85, изменений №2, утверждённого Постановлением Главного государственного санитарного врача Российской Федерации от 25.12.2013 №72, изменений №3, утв. Постановлением Главного государственного санитарного врача Российской Федерации от 24.11.2015 №81)
5.Приказа Минобрнауки России от 31.03.2014 . года № 253 «Об утверждении федерального перечня учебников, рекомендованных к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования»;( в ред. Приказов Минобрнауки России от 08.06.2015 №576, от 28.12.2015 №1529, от 26.01.2016 №38): »
6.Примерной программы основного общего образования по алгебре , под редакцией Т.А. Бурмистровой, Просвещение, 2014г
-
Авторской программы по алгебре и началам анализа под ред.Алимова Ш.А. и др (М, Просвещение 2006г.)
-
Годового календарного учебного графика МБОУ СОШ № 42 с.Сандата на 2016-2017 учебный год.
-
Учебного плана МБОУ СОШ № 42 с.Сандата на 2016-2017 учебный год.
-
Положения о порядке утверждения и структуре рабочих программ учебных предметов, курсов, дисциплин (модулей) педагогических работников МБОУ СОШ №42 с.Сандата .
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: Алгебра, Функции, Уравнения и неравенства, Элементы комбинаторики, теории вероятностей, статистики и логики, вводится линия Начала математического анализа. В рамках указанных содержательных линий решаются следующие задачи:
-
систематизация сведений о числах;
-
изучение новых видов числовых выражений и формул;
-
совершенствование практических навыков и вычислительной культуры,
-
расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
-
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
-
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
-
знакомство с основными идеями и методами математического анализа.
Изучение математики на базовом уровне среднего (полного) общего образования направлено на достижение следующих целей:
Общеучебные цели:
-
создание условий для формирования умения логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки;
-
создание условий для формирования умения ясно, точно и грамотно выражать свои мысли в устной и письменной речи;
-
формирование умения использовать различные языки математики: словесный, символический, графический;
-
формирование умения свободно переходить с языка на язык для иллюстрации, интерпретации, аргументации и доказательства;
-
создание условий для плодотворного участия в работе в группе
-
формирование умения самостоятельно и мотивированно организовывать свою деятельность;
-
формирование умения применять приобретённые знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств при решении задач практического содержания, используя при необходимости справочники;
-
создание условий для интегрирования в личный опыт новой, в том числе самостоятельно полученной информации.
Общепредметные цели:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин (не требующих углубленной математической подготовки), продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственные представления, способность к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средстве моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии через знакомство с историей развития математики, эволюцией математических идей.
Общеучебные умения, навыки и способы деятельности
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
-
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
-
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
-
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
-
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
-
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Задачи курса:
-ввести понятия тригонометрических функций числового аргумента, расширить знания о свойствах функций;
-сформировать представления о производной и научить применять производную к исследованию функций;
- ввести понятия комплексных чисел;
-ввести элементы комбинаторики и теории вероятностей.
2. Требования к уровню подготовки обучающихся.
В результате изучения математики на базовом уровне выпускник средней школы должен: знать/понимать:
-
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
-
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
-
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
-
вероятностный характер различных процессов окружающего мира;
уметь:
-
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
-
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
-
определять значение функции по значению аргумента при различных способах задания функции;
-
строить графики изученных функций;
-
описывать по графику и в простейших случаях по формуле2 поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
-
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
-
вычислять производные и первообразные элементарных функций, используя справочные материалы;
-
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
-
вычислять в простейших случаях площади с использованием первообразной;
-
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
-
составлять уравнения и неравенства по условию задачи;
-
использовать для приближенного решения уравнений и неравенств графический метод;
-
изображать на координатной плоскости множества решений простейших уравнений и их систем;
-
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
-
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства
-
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
-
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
-
построения и исследования простейших математических моделей;
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера.
ТРЕБОВАНИЯ К МАТЕМАТИЧЕСКОЙ ПОДГОТОВКЕ УЧАЩИХСЯ 11 КЛАССА ПО АЛГЕБРЕ
В результате изучения главы «Тригонометрические функции» учащиеся должны
знать:
-
что является областью определения и областью значений функций y = sin x, y = cos x, y = tg x;
-
определение периодической функции;
-
основные свойства тригонометрических функций y = sin x, y = cos x, y = tg x;
уметь:
-
строить графики функций y = sin x, y = cos x, y = tg x и распознавать функции по данному графику;
-
по графику уметь определять свойства тригонометрических функций;
-
находить область определения и область значений тригонометрической функции, заданной формулой;
-
определять четность и нечетность тригонометрической функции;
-
находить наименьший положительный период тригонометрической функции;
-
решать простейшие тригонометрические уравнения и неравенства с помощью графиков функций.
В результате изучения главы «Производная и ее геометрический смысл» учащиеся должны
знать:
-
определение производной;
-
понимать ее физический и геометрический смысл;
-
основные правила дифференцирования и формулы производных элементарных функций;
-
знать уравнение касательной;
уметь:
-
находить производные функций, заданных формулой;
-
находить значения аргумента при заданных значениях производной функции;
-
находить уравнение касательной к функции в заданной точке;
-
находить угловой коэффициент или угол наклона касательной к функции в заданной точке.
В результате изучения главы «Применение производной к исследованию функций» учащиеся должны
знать:
-
какие свойства функций исследуются с помощью производной;
-
определения точек максимума и минимума, стационарных и критических точек;
уметь:
-
выявлять промежутки возрастания и убывания по графику функции, а также по графику ее производной;
-
находить интервалы монотонности функции, заданной аналитически, исследуя знаки ее производной;
-
применять необходимые и достаточные условия экстремума функции при нахождении точек экстремума;
-
строить график функции с помощью производной;
-
находить наибольшее и наименьшее значения функции.
В результате изучения главы «Интеграл» учащиеся должны:
знать:
-
определение первообразной, правила нахождения и таблицу первообразных;
-
определение интеграла и формулу Ньютона-Лейбница;
-
понимать, что такое криволинейная трапеция;
уметь:
-
применять вышеперечисленные знания к нахождению площадей криволинейных трапеций.
В результате изучения главы «Комбинаторика. Элементы теории вероятности. Статистика» учащиеся должны
знать:
-
правило произведения;
-
понятия перестановки, размещения, сочетания;
-
формулу бинома Ньютона;
-
определения случайного события, достоверного события, невозможного события, противоположных событий;
-
понятия суммы и произведения событий, вероятности события, независимого события;
-
теорему о сумме двух несовместных событий
-
понятия относительной частоты события и статистической вероятности;
-
понятия случайной величины, моды, медианы, среднего выборки, размаха выборки;
-
понятия отклонения от среднего, среднего квадратичного отклонения, дисперсии выборки;
уметь:
-
извлекать информацию, представленную в таблицах, на диаграммах, на графиках; составлять таблицы распределения; строить диаграммы и графики, полигоны частот;
-
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила произведения, а также различных комбинаторных конфигураций: перестановок, размещений, сочетаний;
-
записывать разложения бинома Ньютона;
-
определять, каким событием является данное: достоверным, невозможным или случайным, какие события из данных являются несовместными, какие события из данных являются противоположными;
-
находить частоту события, моду, медиану ,среднее выборки, размах и дисперсию выборки, среднее квадратичное отклонение величины;
-
в простейших случаях находить вероятности случайных событий, в том числе с использованием комбинаторики
3. СОДЕРЖАНИЕ учебного предмета
1. Повторение курса алгебры 10кл(5часов)
Основные цели: формирование представлений о целостности и непрерывности курса алгебры; овладение умением обобщения и систематизации знаний по основным темам курса алгебры 10 класса с целью выявления уровня сформированности математической грамотности, развитие логического, математического мышления и интуиции, творческих способностей в области математики
2. Тригонометрические функции
Область определения и множество значений тригонометрических функций. Чётность, нечётность, периодичность тригонометрических функций. Свойства и графики функций y = cos x, y = sin x, y = tg x.
Основные цели: формирование представлений об области определения и множестве значений тригонометрических функций, о нечётной и чётной функциях, о периодической функции, о периоде функции, о наименьшем положительном периоде; формирование умений находить область определения и множество значений тригонометрических функций сложного аргумента, представленного в виде дроби и корня; овладение умением свободно строить графики тригонометрических функций и описывать их свойства;
3.Производная и её геометрический смысл.
Производная, определение производной. Производные суммы, произведения и частного. Производная степенной функции с целым показателем. Производные некоторых элементарных функций. Геометрический смысл производной.
Основные цели:
-
ввести понятие производной;
-
научить находить производные функций в случаях, не требующих трудоемких выкладок, научить находить уравнение касательной к графику функции.
При введении понятия производной и изучении ее свойств следует опираться на наглядно-интуитивные представления учащихся о приближении значений функции к некоторому числу, о приближении участка кривой к прямой линии и т. п.
Формирование понятия предела функции, а также умение воспроизводить доказательства каких-либо теорем в данном разделе не предусматриваются. В качестве примера вывода правил нахождения производных в классе рассматривается только теорема о производной суммы, все остальные теоремы раздела принимаются без доказательства. Важно отработать достаточно свободное умение применять эти теоремы в несложных случаях.
В ходе решения задач на применение формулы производной сложной функции можно ограничиться случаем f(kx + Ь): именно этот случай необходим далее.
4. Применение производной к исследованию функций.
Возрастание и убывание функции. Экстремумы функции. Наибольшее и наименьшее значения функции. Применение производной к построению графиков функций и решению задач на отыскание наибольшего и наименьшего значений.
Основная цель:
-
ознакомить с простейшими методами дифференциального исчисления;
-
выработать умение применять их для исследования функций и построения графиков.
Опора на геометрический и механический смысл производной делает интуитивно ясными критерии возрастания и убывания функций, признаки максимума и минимума.
Основное внимание должно быть уделено разнообразным задачам, связанным с использованием производной для исследования функций. Остальной материал (применение производной к приближенным вычислениям, производная в физике и технике) дается в ознакомительном плане.
5. Первообразная и интеграл
Первообразная. Первообразные степенной функции с целым показателем (п -1), синуса и косинуса. Простейшие правила нахождения первообразных.
Площадь криволинейной трапеции. Интеграл. Формула Ньютона - Лейбница. Применение интеграла к вычислению площадей и объемов.
Основные цели:
-
ознакомить с интегрированием как операцией, обратной дифференцированию;
-
показать применение интеграла к решению геометрических задач.
Задача отработки навыков нахождения первообразных не ставится, упражнения сводятся к простому применению таблиц и правил нахождения первообразных.
Интеграл вводится на основе рассмотрения задачи о площади криволинейной трапеции и построения интегральных сумм. Формула Ньютона - Лейбница вводится на основе наглядных представлений.
В качестве иллюстрации применения интеграла рассматриваются только задачи о вычислении площадей и объемов. Следует учесть, что формула объема шара выводится при изучении данной темы и используется затем в курсе геометрии.
Материал, касающийся работы переменной силы и нахождения центра масс, не является обязательным.
При изучении темы целесообразно широко применять графические иллюстрации.
6. Элементы комбинаторики
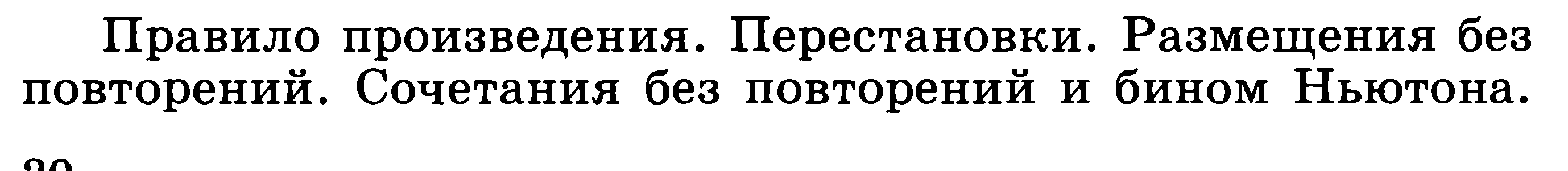 .
.
Основные цели:
-
формирование представлений о научных, логических, комбинаторных методах решения математических задач;
-
формирование умения анализировать, находить различные способы решения одной и той же задачи, делать выводы;
-
развитие комбинаторно-логического мышления.
7. Знакомство с вероятностью
Элементарные и сложные события. Рассмотрение случаев: вероятность
суммы несовместных событий, вероятность противоположного события.
Понятие о независимости событий. Вероятность и статистическая
частота наступления события. Решение практических задач с
применение вероятностных методов.
Основные цели:
-
формирование представления о теории вероятности, о понятиях: вероятность, испытание, событие (невозможное и достоверное), вероятность событий, объединение и пересечение событий, следствие события, независимость событий;
-
формирование умения вычислять вероятность событий, определять несовместные и противоположные события;
-
овладение умением выполнять основные операции над событиями;
-
овладение навыками решения практических задач с применением вероятностных методов.
8. Итоговое повторение курса алгебры и начал анализа, подготовка к ЕГЭ
Уметь:
-
определять значение функции по значению аргумента при различных способах задания функции;
-
строить графики изученных функций;
-
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
-
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
-
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
-
вычислять производные и первообразные элементарных функций, используя справочные материалы;
-
исследовать в простейших случаях функции на монотонность, находить наибольшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
-
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы.
Место предмета в учебном плане
Федеральный базисный учебный план для образовательных учреждений Российской Федерации отводит не менее 280 часов для обязательного изучения математики на базовом уровне ступени среднего общего образования .
Содержание рабочей программы направлено на освоение обучающимися знаний, умений и навыков на базовом уровне, что соответствует образовательной программе МБОУ СОШ № 42 с.Сандата. Она включает в себя все темы, предусмотренные федеральным компонентом государственного образовательного стандарта среднего общего образования по математике и авторской программой учебного курса. В 11 классе на изучение предмета «Алгебра» отводится 102 часа из расчета 3 часа в неделю (34 учебных недели) в т. ч. на контрольные работы отводится 5 ч.
В соответствии с учебным планом и расписанием МБОУ СОШ №42 с. Сандата на 2016-2017 учебный год, а также с государственными праздниками данная программа реализована за 100 часов. Из общего количества часов, отведённых на изучение курса алгебры , мною было сокращено количество часов за счёт уплотнения и блоковой подачи учебного материала по темам повторение в конце учебного года на 2 часа
Контрольные работы составляются с учётом обязательных результатов обучения, даны в трёх уровнях сложности, что позволяет осуществить дифференцированный контроль, с использованием материалов ЕГЭ.
Изменения в примерную или авторскую учебную программу и их обоснование
С целью систематизации и активизации знаний учащихся в начале учебного года проводятся уроки вводного повторения. Часы на повторение в начале учебного года перенесены из часов, выделенных программой на итоговое повторение.(добавлено 3 часа)
Преобладающими формами текущего контроля выступают письменный опрос (самостоятельные и контрольные работы, тестирование), устный опрос.
приложение № 2
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
_по алгебре и_началам анализа_
(учебного предмета, курса)
на 2016-2017 учебный год
11 класс
Учитель _Сибирякова В.В.
Общее количество часов на предмет по учебному плану 99 часов.
Из них на:
I четверть-24 часа
II четверть-24 часа
III четверть-30часов
IV четверть-21час
По 3 часа в неделю.
Всего учебных недель 34
Планирование составлено на основе_«Программы общеобразовательных учреждений 2011 года» «Алгебра 10 - 11 классы», составитель Т.А.Бурмистрова.
Учебник_Алгебра и начала математического анализа10-11кл, Ш.А.Алимов, Ю.М.Колягин, М.Ф.Ткачёва и др, Москва «Просвещение», 2012г
(название, автор, издательство, год издания)
Тематическое планирование алгебре и началам анализа в11классе (3часа в неделю, всего )
Виды и формы контроля: ОСР - обучающая самостоятельная работа ДРЗ - дифференцированное решение задач, ФО- фронтальный опрос ИДР - индивидуальная работа у доски ТЗ - творческое задание ИРК - индивидуальная работа по карточкам СР - самостоятельная работа, ПР - проверочная работа Т - тестовая работа, ПДЗ- проверка домашнего задания, КИМ-работа с материалами ЕГЭОсновные виды деятельности
учащихся
Виды и формы контроля
план
факт
1 четверть
Повторение курса алгебры 10 класса (5 часов)
1
5.09
Вводное повторение. Степени и корни.
1
Решать рациональные, показательные, логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
Использовать для приближённого решения уравнений и неравенств графический метод; Изображать на координатной плоскости множества решений простейших уравнений и их систем
Систематизация учебного материала. Работа с раздаточным материалом. Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе. Пошаговый контроль правильности и полноты выполнения алгоритма действия, плана решения текстовой задачи,
Уст счёт, ФО,
2
6.09
Показательная функция. Показательные уравнения и неравенства.
1
ОСР
3
7.09
Логарифмическая функция. Логарифмические уравнения и неравенства.
1
ФО,
ПДЗ , ТЗ
4
12.09
Тригонометрические формулы.
1
ПДЗ ,Т
5
13.09
Входной контроль.
1
кр
Тригонометрические функции 14 часов
ФО,
ПДЗ , ТЗ
6
14.09
Анализ контрольной работы. Область определения тригонометрических функций.
1
Находить область определения и множество значений тригонометрических функций, заданных формулой;
-
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера. Слушание объяснений учителя.
ПДЗ , ОСР
7
19.09
Множество значений тригонометрических функций.
1
-
Самостоятельная работа с учебником. Выполнение заданий по разграничению понятий.
ФО, ИРК
8
20.09
Чётность и нечётность тригонометрических функций.
исследовать на чётность и нечётность, находить наименьший положительный период тригонометрической функции;
Слушание объяснений учителя. Выполнение заданий по разграничению понятий.
ФО, ОСР
9
21.09
Периодичность тригонометрических функций
ПДЗ , Т
10
26.09
Свойства функции у= cos х и её график
Использовать основные свойства тригонометрических функций для построения их графиков и решения уравнений и неравенств. решать простейшие тригонометрические уравнения и неравенства с помощью графиков функций. Знать,
основные свойства тригонометрических функций y = sin x, y = cos x, y = tg x;
Слушание объяснений учителя. Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ДРЗ, ИРК
11
27.09
Свойства функции у= cos х и её график
Самостоятельная работа с учебником. Выполнение заданий по разграничению понятий.
ФО, ИРК
12
28.09
Свойства функции у= cos х и её график
ИДР, ОСР,
13
3.10
Свойства функции у = sin x и её график
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
ПДЗ, СР, ИДР
14
4.10
Свойства функции у = sin x и её график
ДРЗ,
ФО, ИРК
15
5.10
Свойства функции у= tq x и её график
Слушание объяснений учителя. Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
ПДЗ, СР
16
10.10
Свойства функции у= tq x и её график
ДРЗ,
ФО,
17
11.10
Обратные тригонометрические функции
Иметь представление об обратных тригонометрических функциях.
Слушание объяснений учителя.
ОСР
18
12.10
Урок обобщения и систематизации знаний
Урок систематизации знаний.
Систематизация учебного материала.
ДРЗ,
ФО, ИРК
19
17.10
Контрольная работа №1 по теме «Тригонометрические функции»
Урок контроля и систематизации знаний.
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
КР
Производная и её геометрический смысл. 16 часов
20
18.10
Анализ контрольной работы. Понятие производной и ее механический смысл.
иметь представление о пределе и непрерывности функции, знать определение производной, простейшие правила вычисления производных, находить производные элементарных функций, пользуясь таблицей производных; находить производные элементарных функций, пользуясь правилами дифференцирования; освоить технику дифференцирования;
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
Слушание объяснений учителя.
ПДЗ, ОСР
21
19.10
Вычисление производной с помощью определения.
ДРЗ,
ФО,
22
24.10
Производная степенной функции.
Слушание объяснений учителя. Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
КИМ
23
25.10
Готовимся к ЕГЭ. Вычисление производной степенной функции.
ДРЗ,
ФО, ИРК
24
26.10
Правила дифференцирования и их вывод.
ПДЗ, СР
2 четверть
25
7.11
Готовимся к ЕГЭ. Вычисление производной суммы и разности.
находить производные элементарных функций, пользуясь правилами дифференцирования; освоить технику дифференцирования;
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ДРЗ,
ФО, ИРК
ДРЗ
26
8.11
Готовимся к ЕГЭ. Вычисление производной произведения и дроби.
ФО , КИМ
27
9.11
Производные некоторых элементарных функций.
овладеть умениями находить производную любой комбинации элементарных функций;
-
Построение гипотезы на основе анализа имеющихся данных.
ОСР
28
14.11
Готовимся к ЕГЭ. Производные некоторых элементарных функций
ИРК
29
15.11
Готовимся к ЕГЭ. Производные некоторых элементарных функций
ФО , КИМ ИРК
30
16.11
Геометрический смысл производной.
усвоить геометрический смысл производной; овладеть навыками составления уравнения касательной к графику функции при дополнительных условиях, нахождения углового коэффициента касательной, точки касания
Слушание объяснений учителя.
ДРЗ
31
21.11
Готовимся к ЕГЭ. Геометрический смысл производной.
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ФО , КИМ
32
22.11
Готовимся к ЕГЭ. Геометрический смысл производной.
ИРК
33
23.11
Урок обобщения и систематизации знаний
ФО, ИРК
34
28.11
Урок обобщения и систематизации знаний
ДРЗ
35
29.11
Контрольная работа №2 по теме «Производная и её геометрический смысл.»
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
кр
Применение производной к исследованию функций. 16 часов
36
30.11
Анализ контрольной работы. Возрастание и убывание функции
выявлять промежутки возрастания и убывания по графику функции, а также по графику ее производной; находить интервалы монотонности функции, заданной аналитически, исследуя знаки ее производной;
Слушание объяснений учителя. Сравнение разных приёмов вычислений, решения задачи
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ОСР
37
5.12
Готовимся к ЕГЭ. Возрастание и убывание функции
ФО , КИМ ИРК
38
6.12
Готовимся к ЕГЭ. Возрастание и убывание функции
ДРЗ , КИМ
39
7.12
Экстремумы функции
применять необходимые и достаточные условия экстремума функции при нахождении точек экстремума;
Слушание объяснений учителя.
ИРК
40
12.12
Готовимся к ЕГЭ. Экстремумы функции.
ФО, ИРК
41
13.12
Готовимся к ЕГЭ. Экстремумы функции
-
слушают и вступают в диалог, планируют учебное сотрудничество с учителем и сверстниками, находят способы решения конфликтов, владеют монологической и диалогической формами речи. Решение экспериментальных задач.
Сравнение разных приёмов вычислений, решения задачи
Решение экспериментальных задач. Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ФО , КИМ
42
14.12
Применение производной к построению графиков функций
Строить графики изучаемых зависимостей, читать графики в ходе фронтальной работы, работы с учебником, самостоятельной дифференцированной работы.
ОСР
43
19.12
Применение производной к построению графиков функций
ИРК
44
20.12
Применение производной к построению графиков функций
ДРЗ
45
21.12
Контрольная работа за 1 полугодие по материалам ЕГЭ.
Исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функций,
кр
46
26.12
Наибольшее и наименьшее значение функции
ИРК
47
27.12
Готовимся к ЕГЭ. Наибольшее и наименьшее значение функции
ФО , КИМ
48
28.12
Готовимся к ЕГЭ. Наибольшее и наименьшее значение функции. Выпуклость графика функции, точки перегиба
Исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функций,
ДРЗ
3 четверть
49
11.01
Готовимся к ЕГЭ. Выпуклость графика функции, точки перегиба.
Исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функций,
Слушание объяснений учителя.
Сравнение разных приёмов вычислений, решения задачи
ФО , КИМ
50
16.01
Урок обобщения и систематизации знаний
ИРК
51
17.01
Контрольная работа №3 по теме «Применение производной к исследованию функций.»
Урок контроля и систематизации знаний
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
кр
Интеграл. 13 часов
52
18.01
Анализ контрольной работы . Первообразная
Вычислять первообразные элементарных функций, используя справочные материалы;
Слушание объяснений учителя. Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ОСР
53
23.01
Первообразная
54
24.01
Правила нахождения первообразных
ФО, ИРК
55
25.01
Правила нахождения первообразных
ИРК
56
30.01
Правила нахождения первообразных
ДРЗ
57
31.01
Площадь криволинейной трапеции и интеграл
Вычислять в простейших случаях площади с использованием первообразной;
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
ФО , КИМ
58
1.02
Площадь криволинейной трапеции и интеграл
59
6.02
Площадь криволинейной трапеции и интеграл
ИРК
60
7.02
Вычисление интегралов.
61
8.02
Вычисление площадей с помощью интегралов.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально-экономических и физических, на наибольшее и наименьшее значения, на нахождение скорости и ускорения.
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
ФО , КИМ
62
13.02
Решение задач по теме «интеграл»
ФО, ИРК
63
14.02
Решение задач по теме «интеграл»
ДРЗ
64
15.02
Контрольная работа № 4 «Интеграл»
кр
Элементы комбинаторики. 10часов
65
20.02
Анализ контрольной работы. Работа над ошибками. Правило произведения
Решать комбинаторные задачи путем систематического перебора возможных вариантов
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
ОСР
66
21.02
Перестановки.
Решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ФО , КИМ
67
22.02
Размещения
ДРЗ
68
27.02
Размещения.
Решать простейшие комбинаторные задачи с использованием известных формул;
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
ФО, ИРК
69
28.02
Сочетания и их свойства
ФО , КИМ
70
1.03
Сочетания и их свойства
ИРК
71
6.03
Бином Ньютона
записывать разложения бинома Ньютона;
ОСР
72
7.03
Бином Ньютона
73
13.03
Урок обобщения и систематизации знаний.
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила произведения, а также различных комбинаторных конфигураций: перестановок, размещений, сочетаний;
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ДРЗ
74
14.03
Контрольная работа № 5 «Элементы комбинаторики».
кр кр
Знакомство с вероятностью. 9 часов
75
15.03
События. Комбинации событий. Противоположное событие.
определять, каким событием является данное: достоверным, невозможным или случайным, какие события из данных являются несовместными, какие события из данных являются противоположными;Вычислять в простейших случаях вероятности событий на основе подсчёта числа исходов
76
20.03
Вероятность события.
ФО , КИМ
77
21.03
Сложение вероятностей
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
78
22.03
Сложение вероятностей
ИРК
4 четверть
79
3.04
Независимые события. Умножение вероятностей
в простейших случаях находить вероятности случайных событий, в том числе с использованием комбинаторики
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ФО , КИМ
80
4.04
Независимые события. Умножение вероятностей
ИРК
81
5.04
Статистическая вероятность
ОСР
82
10.04
Статистическая вероятность
ДРЗ
83
11.04
Контрольная работа № 5 «Элементы теории вероятности
кр
Итоговое повторение курса алгебры и начал анализа , подготовка к ЕГЭ. 16часов
84
12.04
Готовимся к ЕГЭ. Действительные числа и вычисления. Вычисление процентов.
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ФО , КИМ
85
17.04
Готовимся к ЕГЭ. Действительные числа и вычисления.
ФО , КИМ
86
18.04
Готовимся к ЕГЭ. Преобразование выражений.
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
ФО , КИМ
87
19.04
Готовимся к ЕГЭ. Преобразование выражений.
ФО , КИМ ИРК
88
24.04
Готовимся к ЕГЭ. Решение уравнений и неравенств.
Решать рациональные, показательные, логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы; Изображать на координатной плоскости множества решений простейших уравнений и их систем
ФО , КИМ
89
25.04
Готовимся к ЕГЭ. Решение уравнений и неравенств.
ФО , КИМ
90
26.04
Готовимся к ЕГЭ. Решение текстовых задач.
Строить, исследовать математические модели, решать составленные уравнения, интерпретировать полученный результат.
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
ДРЗ
91
2.05
Готовимся к ЕГЭ. Решение текстовых задач.
ФО , КИМ
92
3.05
Готовимся к ЕГЭ. Решение текстовых задач.
ФО , КИМ
93
10.05
Готовимся к ЕГЭ. Графики реальных зависимостей, диаграммы.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков; анализа информации статистического характера
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ФО , КИМ
94
15.05
Готовимся к ЕГЭ. Применение производной.
ИРК
95
16.05
Итоговая контрольная работа по материалам ЕГЭ.
кр
96
17.05
Готовимся к ЕГЭ. Применение производной к исследованию функций.
Исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функций, применение геометрическго смысла производной; составление уравнения касательной к графику функции, нахождение углового коэффициента касательной, точки касания
Поиск, обнаружение и устранение ошибок логического (в ходе решения) и арифметического (в вычислении) характера
ФО , КИМ
97
22.05
Готовимся к ЕГЭ. Применение производной.
ИРК
98
23.05
Готовимся к ЕГЭ. Геометрический смысл производной.
Планирование хода решения задачи, выполнения задания на вычисление, Поиск необходимой информации в учебной и справочной литературе
ДРЗ
99
24.05
Заключительный урок-беседа по курсу по курсу алгебры.
ФО , КИМ
График
проведения ЗАЧЁТОВ, практических и контрольных работ
по плану
по факту
1 четверть
1
Входная контрольная работа
13.09
2
Контрольная работа № 1 «Тригонометрические функции»
17.10
2 четверть
3
Контрольная работа № 2 по теме «Производная и её геометрический смысл»
29.11
4
Контрольная работа за 1 полугодие по материалам ЕГЭ.
21.12
3 четверть
5
Контрольная работа № 3 по теме «Применение производной к исследованию функций»
17.01
6
Контрольная работа № 4 «Интеграл»
15.02
7
Контрольная работа № 5 «Элементы комбинаторики»
14.03
4 четверть
8
Контрольная работа № 6 «Элементы теории вероятности»
11.04
9
Итоговая контрольная работа по материалам ЕГЭ.
16.05
Критерии и нормы оценки знаний, умений и навыков
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
1) работа выполнена полностью;
2) в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3) в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
1) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
2)допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
1) допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
1) допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
2)работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
-
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
-
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
-
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
-
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
-
отвечал самостоятельно, без наводящих вопросов учителя;
-
возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4»,
если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
-
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
-
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
-
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
-
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
-
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
-
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
-
не раскрыто основное содержание учебного материала;
-
обнаружено незнание учеником большей или наиболее важной части учебного материала;
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
-
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
-
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
-
незнание наименований единиц измерения;
-
неумение выделить в ответе главное;
-
неумение применять знания, алгоритмы для решения задач;
-
неумение делать выводы и обобщения;
-
неумение читать и строить графики;
-
неумение пользоваться первоисточниками, учебником и справочниками;
-
потеря корня или сохранение постороннего корня;
-
отбрасывание без объяснений одного из них;
-
равнозначные им ошибки;
-
вычислительные ошибки, если они не являются опиской;
-
логические ошибки.
К негрубым ошибкам следует отнести:
-
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
-
неточность графика;
-
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
-
нерациональные методы работы со справочной и другой литературой;
-
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
-
нерациональные приемы вычислений и преобразований;
-
небрежное выполнение записей, чертежей, схем, графиков.
Контроль ЗУН предлагается при проведении математических диктантов, практических работ, самостоятельных работ обучающего и контролирующего вида, контрольных
Материально-техническое обеспечения образовательного процесса
а) Книгопечатные.
-
Программы общеобразовательных учреждений 2011 года» «Алгебра 10 - 11 классы», составитель Т.А.Бурмистрова
2.«Алгебра и начала анализа 10 - 11 класс», авторы: Алимов Ш. А., Колягин,Ю.М., Сидоров Ю.В., Фёдорова Н.Е., Шабунин М.И. Издательство «Просвещение», 2012 год.
-
«Изучение алгебры и начал анализа 10-11кл.» Фёдорова Н.Е.
-
«Тематический контроль по алгебре и началам анализа
10-11кл.» тесты, ДенищеваЛ.О.,
-
«Самостоятельные и контрольные работы» Ершова А.П.,
-
«Карточки для коррекции знаний» Левитас Г.Г.,
-
Поурочные планы Григорьева Г.И.
-
«Контрольные и проверочные работы» Звавич Л.И.
-
Сборники для подготовки к ЕГЭ
10. Уроки алгебры и начал анализа в 10 классе. / Т.Л. Афанасьева, Л.А. Тапилина. Пособие для учителей. / Волгоград, «Учитель».
б) Печатные пособия.
Таблицы «Алгебра 10 - 11 классы»
в) технические средства обучения.
СД. «Алгебра 10-11».
СД. «Тригонометрия не для отличников».
СД. «Шпаргалки для старшеклассников».
СД «Алгебра не для отличников»
Мультимедийные презентации
Привлечение ресурса Интернет,
Интернет-ресурсы:
-
standart.edu.ru [Сайт Федерального Государственного образовательного стандарта];
2. school-collection.edu.ru [Единая коллекция цифровых образовательных ресурсов];
3. pedsovet.su [Сайт сообщества взаимопомощи учителей];
4. festival.1september.ru [Фестиваль педагогических идей «Открытый урок»];
-
www.1september.ru</</font>
д) Учебно - практическое и учебно - лабораторное оборудование.
-
Набор предметных картинок.
-
Наборное полотно.
-
Демонстрационная оцифрованная линейка.
-
Демонстрационный чертежный треугольник.
е) Оборудование класса
-
Шкафы - 6 штук.
-
Столы ученические - 16 штук.
-
Стулья ученические - 16 штук.
-
Стол учителя - 1 штука.
-
Стул мягкий - 1 штука.
-
Классная доска с набором приспособлений для крепления таблиц.
-
Магнитная доска.
Контрольная работа №1

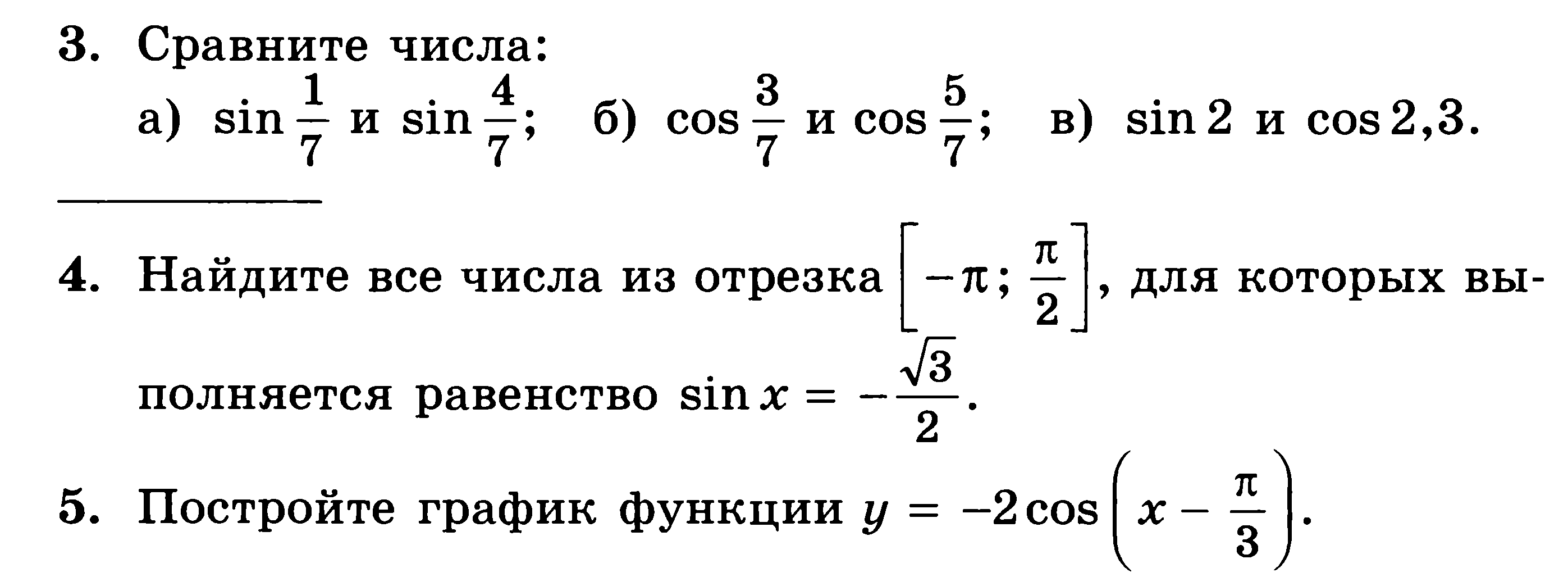
Контрольная работа №2

Контрольная работа №3

Контрольная работа №4
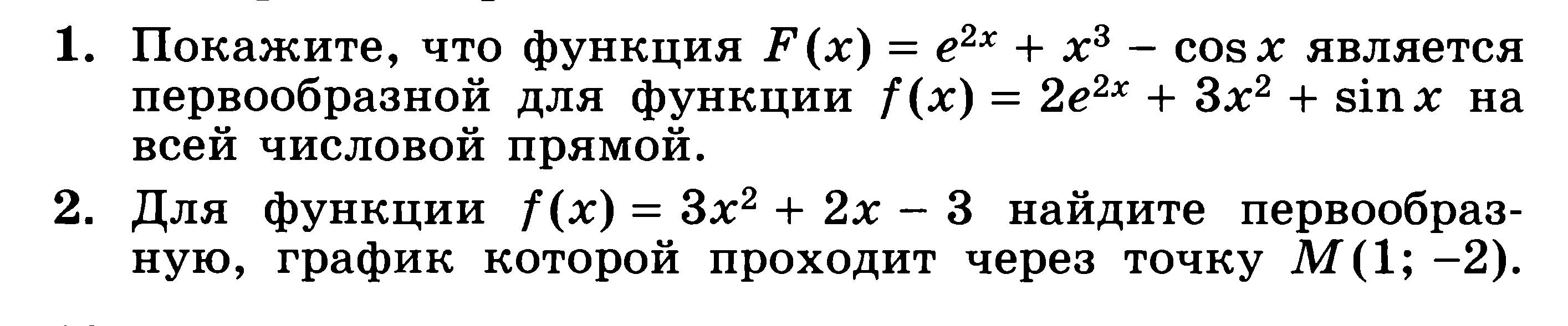

Контрольная работа №5

Контрольная работа №6

