Разработка урока по теме Применение векторов к решению задач. Средняя линия трапеции.

Г - 9 класс Урок № 7

Тема: «Применение векторов к решению задач. Средняя линия трапеции».

Цели урока:

1. Дидактическая: на конкретных примерах показать применение векторов при решении геометрических задач; ввести понятия средней линии трапеции; доказать теорему о средней линии трапеции с помощью векторов.

2. Развивающая: развивать логическое мышление учащихся, учить решать задачи; развивать воображение - репродуктивное, творческое, образное; абстрактное мышление, умение обобщать.

3. Воспитательная: нравственное воздействие, воспитание культуры умственного труда, культуры общения.

Обучающиеся должны:

Знать, действия производимые с векторами, понятие средней линии трапеции, теорему о средней линии трапеции.

Уметь вычислять среднюю линию трапеции, решать задачи с помощью векторов.

Ход урока.

1. Организационный момент.

Сообщение темы и целей урока.

2. Актуализация знаний и умений обучающихся.

   1. Проверка выполнения домашнего задания. Разбор нерешенных заданий.

   2. Повторение изученного материала.

1. Ответить на вопросы на с. 213-214.

2. Проверка усвоения учащимися материала.

1. Устно ответить на вопросы:

</ 1) Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы и и противоположно направленные векторы и .

2) Какой вектор называется произведением данного вектора на данное число?

3) Могут ли векторы и быть неколлинеарными?

4) Сформулируйте основные свойства умножения вектора на число.

2. Решить задачу на доске и в тетрадях по готовому чертежу:

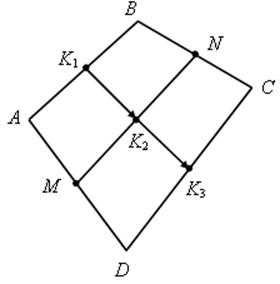
Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM : MD = BN : NC = 3 : 4.

Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.

Решение

Пусть K1 - середина AB, K2 - середина MN, K3 - середина CD. Согласно задаче 2 из п. 84 имеем 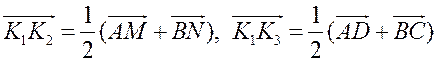. Из условия следует, что 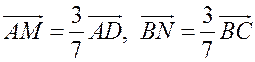, поэтому .

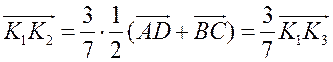Таким образом, векторы и коллинеарные, и, значит, точки K1, K2 и K3 лежат на одной прямой.

3. Изучение нового материала.

1. Определение трапеции. Виды трапеций.

2. Определение средней линии трапеции.

3. Доказательство теоремы о средней линии трапеции.

Доказательство оформить на доске и в тетрадях в виде следующей краткой записи:

Дано: ABCD - трапеция, AD || BC, M - середина стороны AB; N - середина стороны CD (рис. 266 учебника).

Доказать: MN || AD, MN = .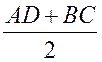

Доказательство.

1) Согласно рассмотренной в классе задаче 1 .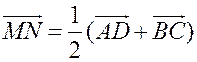

2) Так как , то и, значит, MN || AD.

3) Так как , то = AD + BC, поэтому MN = (AD + BC).

4. Формирование умений и навыков.

Работа по учебнику.

1. Векторы могут использоваться для решения геометрических задач. Рассмотрим вспомогательную задачу.

2. Разобрать решение задачи 1 на с. 208 учебника по рис. 264.

3. Решить задачу 2. Точки M и N - середины сторон AB и CD четырехугольника ABCD. Докажите, что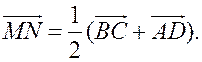

Решение

Пусть О - произвольная точка. Согласно задаче 1 из п. 84 имеем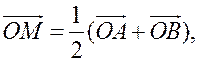 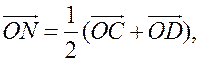поэтому .

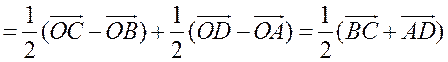Примечание. Результат задачи 2 можно использовать при доказательстве теоремы о средней линии трапеции на следующем уроке.

4. 1. Решить на доске и в тетрадях задачу № 793.

Решение

Пусть a и b - основания трапеции, тогда а + b = 48 - (13 + 15) = 20 (см); средняя линия MN = 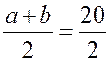= 10 (см).

Ответ: 10 см.

2. Решить задачу № 795.

3. Решить задачу № 799 на доске и в тетрадях.

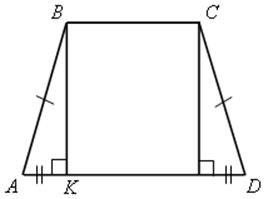
Решение

Пусть BK - перпендикуляр, проведенный к основанию AD данной трапеции.

Тогда KD = AD - AK.

Но AK = 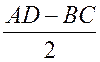, поэтому KD = AD -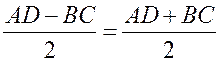, то есть отрезок KD равен средней линии трапеции. Значит, средняя линия трапеции равна 7 см.

Ответ: 7 см.

5. Решить задачу 3. Точка С лежит на отрезке AB, причем АС : СВ = 2 : 3. Докажите, что для любой точки О справедливо равенство

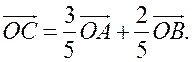
Решение

По условию AC:CB=2 : 3,поэтому Но Следовательно, откуда получается

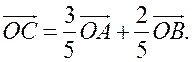
Примечание. Задача 3 является частным случаем более общей задачи 806.

6. Решить задачу № 786 на доске и в тетрадях.

Решение

Так как точка А1 - середина стороны ВС, то .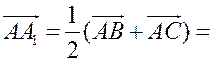

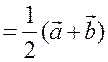Далее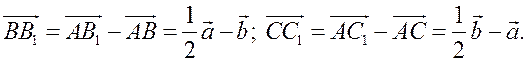

7. При наличии времени решить задачу 4.

Точки K, L, M, N - середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q - середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.

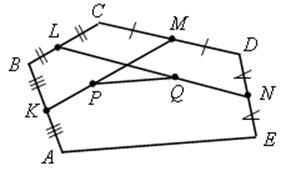
Решение

Пусть О - произвольная точка. Согласно задаче 1 из п. 84 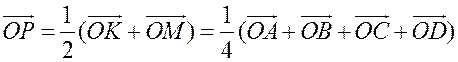. Аналогично, .

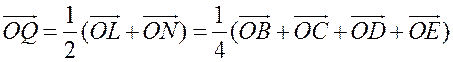Из этих равенств следует, что 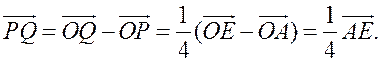Отсюда следует, что PQ || AE и PQ = AE.

5. Итоги урока.

Подвести итоги урока, выставить отметки обучающимся за урок.

В результате изучения параграфа обучающиеся должны знать, какой вектор называется произведением вектора на число; уметь формулировать свойства умножения вектора на число; знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции; уметь решать задачи типа №№ 782-787; 793-799.

6. Домашнее задание: изучить материал п. 87, 88; ответить на вопросы 18-20, с. 214 учебника; решить задачи №№ 787, 794, 796.

8