Конспект уроку з алгебри для учнів 9 класу з теми:

Урок з алгебри, 9 клас.

Тема уроку: Побудова графіків функцій виду у = за допомогою геометричних перетворень.

Мета уроку: Узагальнити та систематизувати знання учнів про квадратичну функцію. Систематизувати знання учнів про елементарні перетворення графіків функцій. Формувати навички побудови графіків складних функцій.

Розвивати логічне та критичне мислення учнів, графічні навички, просторову уяву, уміння

працювати в команді і в парах.

Виховувати культуру математичної мови та письма, охайність графічних побудов.

Тип уроку: урок засвоєння нових знань.

Обладнання: картки самооцінки, комп'ютерний супровід уроку (слайди).

Технічне обладнання уроку:

1. Ноутбук;

2. Мультимедійний проектор;

3. Екран.

Хід уроку.

I. Мотивація учбової діяльності учнів на уроці.

Постановка мети уроку.

II. Актуалізація опорних знань учнів.

• Слайд № 2. Демонстрація функції у = х² та її графік. Означення квадратичної функції.

№ 2. № 3.

• Слайд № 3. Завдання класу: оберіть із заданих функцій квадратичну.

• Слайд № 4. Повторення функцій, які ви вивчали у 8 класі.

№ 4.

• Презентація: "Перетворення графіків функцій" - "Впізнай мене!"

На слайдах № 5-12 зображено 8 правил геометричних перетворень графіків функцій. Учні повинні вказати формулу функції, графік якої зображений на малюнку.

Наприклад, на наступних слайдах зображено два правила:

1. Побудова графіка функції у = kf(х);

2. Побудова графіка функції у = |f (х)|.

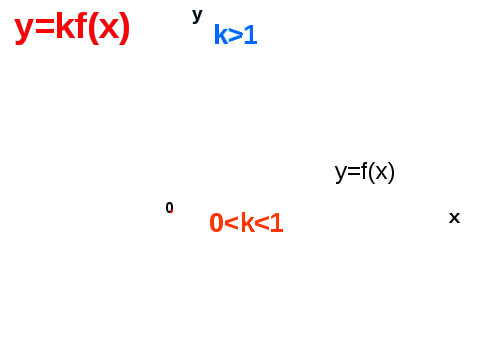
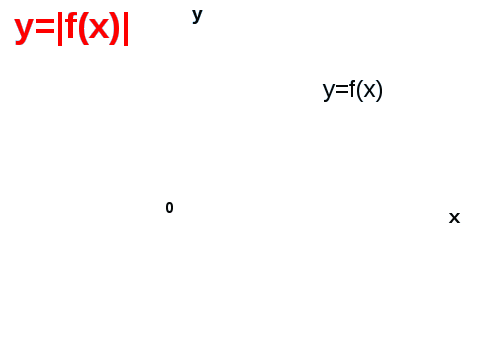
• Презентація: "Побудова графіків квадратичної функції". Самооцінка.

На слайдах № 13 - 19 показано застосування перетворення графіків функцій при побудові графіка квадратичної функції. Наприклад, на наступних слайдах зображено два правила:

1. Побудова графіка функції у = х² - 3;

2. Побудова графіка функції у = 0,5х².

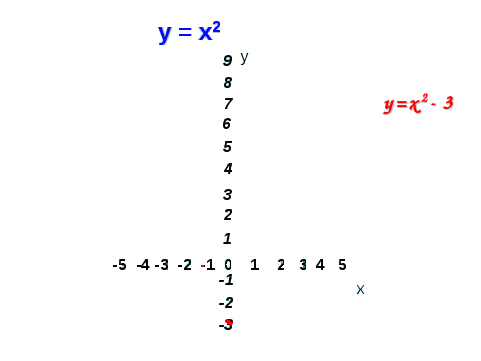
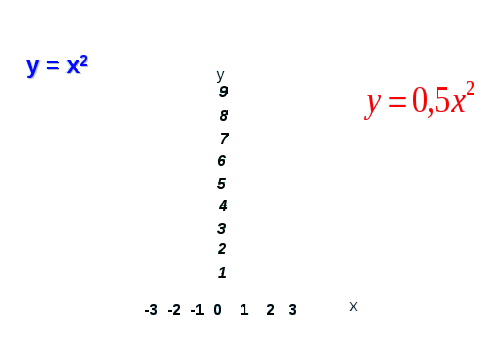
III. Засвоєння нових знань.

• Слайд № 20. Постановка питання: як побудувати графік функції, який потребує декілька перетворень?

у =

• Слайд № 21. Розробка і запис в зошиті алгоритму побудови графіка функції у = 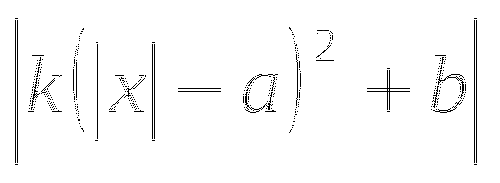за допомогою геометричних перетворень.

1) у = х²;

2) у = kх² (стискання або розтягування у k разів вздовж осі Оу);

3) у = k (х - а)² (паралельне перенесення на а одиниць ліворуч або праворуч вздовж осі Ох);

4) у = k (х - а)² + в (паралельне перенесення на в одиниць вгору або вниз вздовж осі Оу);

5) у = (симетрія частини графіка, що лежить справа від осі Оу відносно цієї осі);

6) у = (симетрія частини графіка, що лежить нижче за вісь Ох відносно цієї осі);

• Слайд № 22. Побудова графіка функції у = 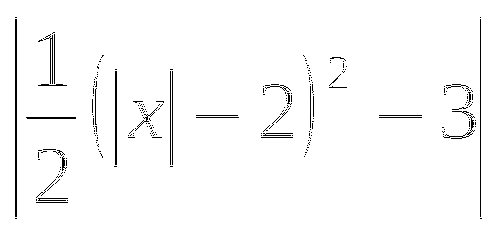за допомогою алгоритма:

1) у = х²;

2) у = х² (стиск в 2 рази вздовж осі Оу);

3) у = (х - 2)² (паралельне перенесення на 2 одиниці праворуч вздовж осі Ох);

4) у = (х - 2)² - 3 (паралельне перенесення на 3 одиниць вниз вздовж осі Оу);

5) у = (симетрія частини графіка, що лежить справа від осі Оу відносно цієї осі);

6) у = (симетрія частини графіка, що лежить нижче за вісь Ох відносно цієї осі);

IV. Формування вмінь та навичок.

• Робота в парах "Розшифруй портрет". Самооцінка.

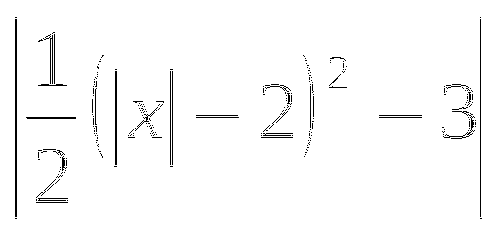
Побудувати графіки функцій:

Завдання для I ряду:

1) у = , якщо х є (-6; 6);

2) у = -, якщо х є (1; 3);

Завдання II ряду:

1) у = + 1, якщо х є (-2; 2);

2) у = -, якщо х є (1; 3);

Завдання III ряду:

1) у = + 7, якщо х є (-6; 6);

2) у = , якщо х є (1; 3).

VІ. Підсумок уроку.

Підведення підсумків уроку. Заключне слово вчителя.