Подготовка к ЕГЭ по математике. Решение задач.

Решение химических задач на смеси и сплавы алгебраическим методом.

Основными методами решения задач на смешивание растворов являются:

• с помощью расчетной формулы,

• правило смешения,

• правило креста,

• графический метод,

• алгебраический метод.

Я исследовала алгебраический метод решения задач на смеси и сплавы. Задачи на смеси, растворы и сплавы входят в обязательный курс школьной математики и встречаются на ЕГЭ. Смесь состоит из основного вещества и примеси. В этих задачах считается, что масса смеси нескольких веществ равна сумме масс компонентов. Процентным содержанием (концентрацией ) вещества в смеси называется отношение его массы к общей массе всей смеси. Эта величина может быть либо в дробях, либо в процентах. Измерять количество компонентов в смеси будем в единицах массы, а не объема. Сумма массовых долей всех компонентов, оставляющих смесь рана единице . Прежде ,чем приступить к разбору конкретных задач, посмотрим какие существуют подходы к их решению. Наиболее распространенный способ - использование таблиц. В решении задач помогает и картинка. Изображаем сосуды с раствором схематично, так как будто вещество и вода в нем на перемешаны между собой , а отделены друг т друга , как в коктейле. Задачи на смеси и сплавы вызывают наибольшие затруднения. В процессе решения каждой такой задачи целесообразно действовать по следующей схеме.

1. Изучение условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.), относительно которых составляем пропорции. Выбирая неизвестные параметры, мы создаем математическую модель ситуации, описанной в условии задачи.

2. Поиск плана решения. Используя условия задачи, определяем все взаимосвязи между данными величинами.

3. Осуществление плана, т.е. оформление найденного решения - переход от словесной формулировки к составлению математической модели.

4. Изучение полученного решения, критический анализ результата.

В большинстве случаев задачи на смеси и сплавы становятся нагляднее, если при их решении использовать схемы, иллюстративные рисунки или вспомогательные таблицы.

Масса раствора М

Концентрация Р

Масса вещества m

1

2

1+2

А сейчас приведу примеры раствора, смеси и сплава.

Раствор.

Задача 1.

В 190 грамм воды добавим 10 грамм уксусной кислоты, получим раствор, масса которого равна 190 + 10 = 200 грамм. Концентрация кислоты (процентное содержание) - это отношение количества уксуса к количеству раствора, записанное в процентах:

Процентное содержание воды:

Смесь.

Задача 2.

У нас есть одно ведро песка и три ведра извести. Смешаем содержимое всех ведер, получим смесь извести с песком, её масса равна 1 + 3 = 4 (единиц массы). Концентрация (процентное содержание песка) - это отношение количества песка к количеству смеси, записанное в процентах:

Процентное содержание извести:

Сплав.

Задача 3.

Имеем сплав меди и свинца, в котором 100 грамм меди и 150 грамм свинца. Концентрация (процентное содержание меди) - отношение количества меди к количеству смеси в процентах:

Как можно заметить, во всех задачах на сплавы, растворы, смеси используется всего одна формула:

где K - процентное содержание чистого вещества в сплаве или растворе,

m - масса чистого вещества

M - масса сплава или раствора.

А теперь посмотрим как решать задачи на практике.

Задача 4. В сосуд, содержащий 5 литров 15%- раствора соли, добавили 7 литров воды. Какова концентрация соли в полученном растворе (в процентах)?

Решение.

Нарисуем таблицу и заполним ее:

1. Для начала определимся, какую неизвестную мы обозначим за х. В нашей задаче удобно за х принять саму искомую величину, т.е. концентрацию соли в полученном растворе.

2. Теперь в таблице заполним все ячейки, которые нам известны.

Масса раствора М

Концентрация Р

Масса вещества m

1

5л

15%

Соль 5*0,15=0,75

2

7л

вода

1+2

12л

Х

Соль5*0,15=0,75

2. Чтобы применить формулу, нам нужно знать массу соли в полученном растворе, а так как масса соли в первом растворе и в полученном одинакова, то можем найти ее:

3. Теперь несложно найти х, подставив данные в формулу:

Ответ: Концентрация соли в полученном растворе - 6,25%.

Задача 5. Сколько килограммов меди нужно добавить к куску бронзы массой 8 кг и содержащему 13% меди, чтобы повысить содержание в нем меди до 25% от общей массы?

Решение.

По условию составим таблицу, считая, что смешали два сплава и второй сплав содержит 100% меди и не содержит остальных компонентов.

1-ый сплав

2- сплав

полученный сплав

медь

13%

100%

25%

бронза

сплав

8кг.

1. Масса меди в первом сплаве

2. Обозначим массу меди во втором сплаве х кг;

3. Масса меди в полученном сплаве (1,04 + х) кг;

4. Масса второго сплава х кг, так как он состоит только из меди, которую в пункте 2 мы обозначили за х кг;

5. Масса полученного сплава (8 + х) кг;

6. Отношение массы меди в полученном сплаве к массе полученного сплава

по условию задачи оно должно быть равно 0,25. Имеем уравнение

Решим его

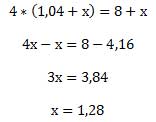
Ответ: 1,28 кг нужно добавить к 1-ой смеси.

Задача 6.

Свежие грибы содержат 90% воды, а сухие - 15% воды. Сколько получится сухих грибов из 34 кг свежих грибов?

Решение.

Свежие грибы

Сухие грибы

вода

90%

15%

«мякоть»

смесь

34 кг.

х кг.

При сушке грибов (ягод, фруктов) происходит испарение воды, то есть масса воды уменьшается, а масса «мякоти» остается постоянной.

1. Процентное содержание «мякоти» в свежих грибах 100% - 90% = 10%;

2. Масса «мякоти»

3. Процентное содержание мякоти в сухих грибах 100% - 15% = 85%;

4. Обозначим массу сушеных грибов за х кг;

5. Отношение массы «мякоти» к массе сушеных грибов 3,4 / х, что по условию задачи равно 0,85.

Имеем уравнение

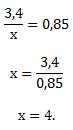
Ответ: Получим 4 кг. сухих грибов.

Задача 7 .

В сосуд, содержащий 7 литров 14-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Решение:

Вот так выглядит краткое условие в рисунке:

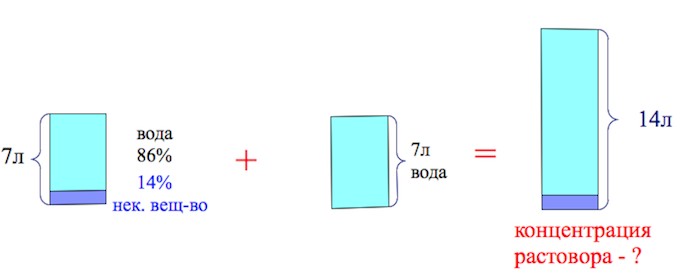
Задача 8.

К 200 г 20%процентного раствора соли добавили 60 г соли. Найдите концентрацию раствора.

Масса раствора

% содержания

Масса вещества

200г

20%

0,2*200=40 г

260 г

х %

60 г

40+60=100 х*260=100

х=100:260=38,5%

Задача 9.

Смешали 30% и 10% растворы соляной кислоты и получили 600 г 15% раствора. Сколько граммов каждого вещества взяли?

Масса раствора

% содержание

Масса вещества

1 раствор

х

30%

0,3х

2 раствор

у

10%

0,1у

600 г

15 %

0,15*600=90

0,3х +0,1у=90 и х+у=600 х=150,у=450Задача 10.

В сосуд, со­дер­жа­щий 5 лит­ров 12-про­цент­но­го вод­но­го рас­тво­ра не­ко­то­ро­го

ве­ще­ства, до­ба­ви­ли 7 лит­ров воды. Сколь­ко про­цен­тов со­став­ля­ет кон­цен-

­тра­ция по­лу­чив­ше­го­ся рас­тво­ра.

Ре­ше­ние.

Кон­цен­тра­ция рас­тво­ра равна

.

Объем ве­ще­ства в ис­ход­ном рас­тво­ре равен литра. При до­бав­ле­нии 7

лит­ров воды общий объем рас­тво­ра уве­ли­чит­ся, а объем рас­тво­рен­но­го ве­ще­ства

оста­нет­ся преж­ним. Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го рас­тво­ра равна:

.

Ответ: 5.

За­да­ча 11.

Сме­ша­ли 4 литра 15-про­цент­но­го вод­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

6 лит­ра­ми 25-про­цент­но­го вод­но­го рас­тво­ра этого жеве­ще­ства. Сколь­ко

про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Кон­цен­тра­ция рас­тво­ра равна . Таким об­ра­зом, кон­цен­тра­ция

по­лу­чив­ше­го­ся рас­тво­ра равна:

Ответ: 21.

За­да­ча 12.

Ви­но­град со­дер­жит 90% влаги, а изюм - 5%. Сколь­ко ки­ло­грам­мов ви­но­гра­да

тре­бу­ет­ся для по­лу­че­ния 20 ки­ло­грам­мов изюма?

Ре­ше­ние.

Ви­но­град со­дер­жит 10% пи­та­тель­но­го ве­ще­ства, а изюм - 95%. По­это­му

20 кг изюма со­дер­жат кг пи­та­тель­но­го ве­ще­ства. Таким об­ра­зом,

для по­лу­че­ния 20 ки­ло­грам­мов изюма тре­бу­ет­ся кг ви­но­гра­да.

Ответ: 190.

За­да­ча 13.

Име­ет­ся два спла­ва. Пер­вый сплав со­дер­жит 10% ни­ке­ля, вто­рой - 30%

ни­ке­ля. Из этих двух спла­вов по­лу­чи­ли тре­тий сплав мас­сой 200 кг,

со­дер­жа­щий 25% ни­ке­ля. На сколь­ко ки­ло­грам­мов масса пер­во­го спла­ва мень­ше

массы вто­ро­го?

За­да­ча 14.

Пер­вый сплав со­дер­жит 10% меди, вто­рой - 40% меди.

Масса вто­ро­го спла­ва боль­ше массы пер­во­го на 3 кг. Из этих двух спла­вов

по­лу­чи­ли тре­тий сплав, со­дер­жа­щий 30% меди. Най­ди­те массу тре­тье­го

спла­ва. Ответ дайте в ки­ло­грам­мах.

Ре­ше­ние.

Пусть масса пер­во­го спла­ва кг, а масса вто­ро­го - кг, масса тре­тье­го

спла­ва - кг. Пер­вый сплав со­дер­жит 10% меди, вто­рой - 40% меди,

тре­тий сплав - 30% меди. Тогда:

Ответ: 9.

За­да­ча 15 .

Име­ют­ся два со­су­да. Пер­вый со­дер­жит 30 кг, а вто­рой - 20 кг рас­тво­ра кис­ло­ты

раз­лич­ной кон­цен­тра­ции. Если этирас­тво­ры сме­шать, то по­лу­чит­ся рас­твор,

со­дер­жа­щий 68% кис­ло­ты.Если же сме­шать рав­ные массы этих рас­тво­ров, то

по­лу­чит­ся рас­твор,со­дер­жа­щий 70% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты

со­дер­жит­ся в пер­вом со­су­де?

За­да­ча 16 .

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 13-про­цент­но­го рас­тво­ра не­ко­то­ро­го

ве­ще­ства с таким же ко­ли­че­ством 17-про­цент­но­го рас­тво­ра этого ве­ще­ства.

Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Про­цент­ная кон­цен­тра­ция рас­тво­ра (мас­со­вая доля) равна . Пусть

масса по­лу­чив­ше­го­ся рас­тво­ра Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го

рас­тво­ра равна:

Ответ: 15.

За­да­ча 17.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 15-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 17-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет

кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

За­да­ча 18.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 20-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 16-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Про­цент­ная кон­цен­тра­ция рас­тво­ра (мас­со­вая доля) равна . Пусть

масса по­лу­чив­ше­го­ся рас­тво­ра Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го

рас­тво­ра равна:

Ответ: 18.

Разбор конкретных текстовых задач №11 ЕГЭЗа­дача ­19.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 14-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 18-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

За­да­ча 20. Сме­ша­ли не­ко­то­рое ко­ли­че­ство 19-про­цент­но­го рас­тво­ра

не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 13-про­цент­но­го рас­тво­ра этого

ве­ще­ства.Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Про­цент­ная кон­цен­тра­ция рас­тво­ра (мас­со­вая доля) равна . Пусть

масса по­лу­чив­ше­го­ся рас­тво­ра Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го рас­тво­ра

равна:

Ответ: 16.

За­да­ние 21 .

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 20-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 14-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Про­цент­ная кон­цен­тра­ция рас­тво­ра (мас­со­вая доля) равна . Пусть

масса по­лу­чив­ше­го­ся рас­тво­ра Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го

рас­тво­ра равна:

Ответ: 17.

За­да­ние 22.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 12-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 18-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

За­да­ние 23.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 18-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 14-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Про­цент­ная кон­цен­тра­ция рас­тво­ра (мас­со­вая доля) равна . Пусть

масса по­лу­чив­ше­го­ся рас­тво­ра Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го

рас­тво­ра равна:

Ответ: 16.

За­да­ние 24.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 16-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 12-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

За­да­ние 25.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 21-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 13-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Про­цент­ная кон­цен­тра­ция рас­тво­ра (мас­со­вая доля) равна . Пусть

масса по­лу­чив­ше­го­ся рас­тво­ра Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го

рас­тво­ра равна:

Ответ: 17.

За­да­ние 26 .

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 12-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 20-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Задача 27.

Сплав олова с медью весом 12 кг содержит 45 % меди. Сколько чистого олова надо добавить , чтобы получить сплав, содержащий 40% меди?

Масса сплава

% содержание меди

% содержание олова

Масса олова

1 сплав

12

45

55

12*0,55=6,6

олово

х

100

х

2 сплав

12+х

40

х

(12+х)*0,6

6,6+х=(12+х)*0,6 х=1,5 кгЗа­да­ние 28.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 11-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 17-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Про­цент­ная кон­цен­тра­ция рас­тво­ра (мас­со­вая доля) равна . Пусть

масса по­лу­чив­ше­го­ся рас­тво­ра Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го

рас­тво­ра равна:

Ответ: 14.

За­да­ние 29 .

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 17-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства

с таким же ко­ли­че­ством 19-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен-

­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Задача 30.

Морская вода содержит 8% по весу соли. Сколько кг пресной воды нужно добавить

к 30 кг морской воды, чтобы содержание соли в последней составило 5%?

Масса морской воды

5содержание соли

Масса соли

1 состав

30

8 %

30*0,08

Пресная вода

х

0%

х*0

2 состав

30+х

5%

(30+х)*0,05

30*0,08=(30+х)0,05 х=18За­да­ние 31.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 21-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства

с таким же ко­ли­че­ством 15-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен-

­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Про­цент­ная кон­цен­тра­ция рас­тво­ра (мас­со­вая доля) равна . Пусть

масса по­лу­чив­ше­го­ся рас­тво­ра Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го

рас­тво­ра равна:

Ответ: 18.

За­да­ние 32.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 11-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 19-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен-

тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Про­цент­ная кон­цен­тра­ция рас­тво­ра (мас­со­вая доля) равна . Пусть

масса по­лу­чив­ше­го­ся рас­тво­ра Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го

рас­тво­ра равна:

Ответ: 15.

За­да­ние 33.

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 13-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 15-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

За­да­ние 34 .

Сме­ша­ли не­ко­то­рое ко­ли­че­ство 19-про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с

таким же ко­ли­че­ством 15-про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов

со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

За­да­ние 35.

Име­ет­ся два рас­тво­ра. Пер­вый со­дер­жит 10% соли, вто­рой - 30% соли. Из этих

двух рас­тво­ров по­лу­чи­ли тре­тий рас­твор мас­сой 200 кг, со­дер­жа­щий 25% соли.

На сколь­ко ки­ло­грам­мов масса пер­во­го рас­тво­ра мень­ше массы вто­ро­го?

Задача 36.

Из 38 тонн сырья второго сорта ,содержащего 25% примесей. После очистки

получается 30 тонн сырья первого сорта. Каков %примесей в сырье первого сорта?

Масса сырья

%содержание

Масса примесей

2 состав

38 т

25

30

примеси

8 т

100

1 сорт

30 т

х

30*0,01х

38*0,25-8=30*0,01х

х=5%



За­да­ние 37.

Сме­шав 43‐про­цент­ный и 89‐про­цент­ный рас­тво­ры кис­ло­ты

и до­ба­вив 10 кг чи­стой воды, по­лу­чи­ли 69‐про­цент­ный рас­твор кис­ло­ты. Если бы

вме­сто 10 кг воды до­ба­ви­ли 10 кг 50‐про­цент­но­го рас­тво­ра той же кис­ло­ты, то

по­лу­чи­ли бы 73‐про­цент­ный рас­твор кис­ло­ты. Сколь­ко ки­ло­грам­мов 43‐

про­цент­но­го рас­тво­ра ис­поль­зо­ва­ли для по­лу­че­ния смеси?

Ре­ше­ние.

Пусть масса 43-про­цент­но­го рас­тво­ра кис­ло­ты - кг, а масса 89-про­цент­но­го

- . Если сме­шать 43-про­цент­ный и 89-про­цент­ный рас­тво­ры кис­ло­ты

и до­ба­вить кг чи­стой воды, по­лу­чит­ся 69-про­цент­ный

рас­твор кис­ло­ты: . Если бы вме­сто 10 кг воды

до­ба­ви­ли кг 50-про­цент­но­го рас­тво­ра той же кис­ло­ты, то по­лу­чи­ли бы 73-

про­цент­ный рас­твор кис­ло­ты:

.

Решая по­лу­чен­ную си­сте­му урав­не­ний:

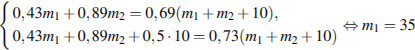
Задача 38.

Смешали некоторое количество 13-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

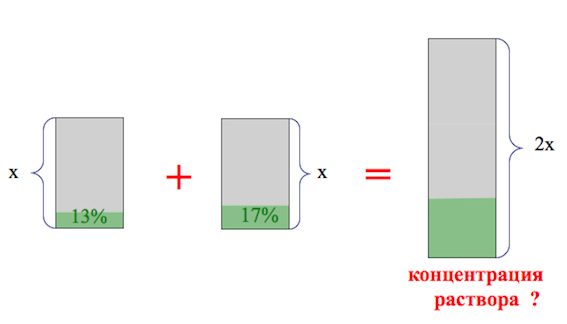
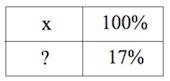
Наконец, составляя последнюю пропорцию, получаем:

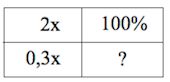
Ответ: 15.

Задача 39.

Имеется два сплава. Первый сплав содержит 10% никеля, второй - 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

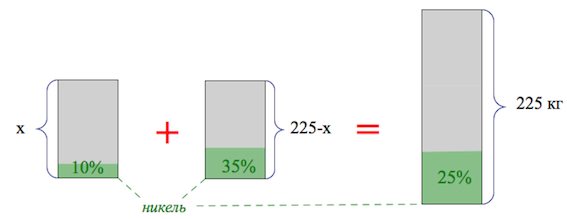
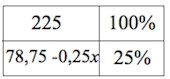
Ответ: 45.

Задача 40.

Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?

.

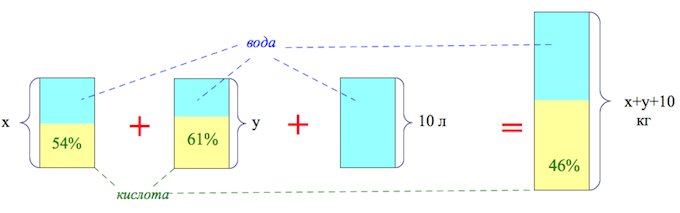
Составим пропорцию:

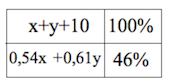
Рассмотрим второй случай.

.

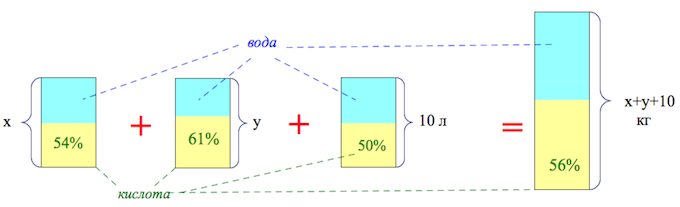
Составим пропорцию:

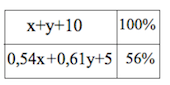
Ответ: 20.

Задача 41.

Имеются два сосуда. Первый содержит 100 кг, а второй - 60 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

Задача 42.

Виноград содержит 90% влаги, а изюм - 5%. Сколько килограммов винограда требуется для получения 40 килограммов изюма?

Решение:

Рисунок наглядно иллюстрирует условие задачи:

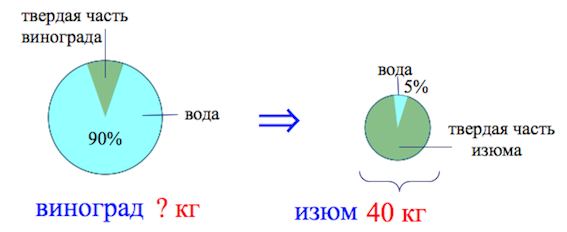
Обратите внимание! Что очень важно понимать для решения данной задачи?

«Твердая часть винограда» = «твердая часть изюма»!

Начнем с изюма.

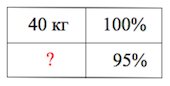
Переходим к винограду.

Твердая часть в винограде занимает 10% веса. Обозначим за кг массу винограда.

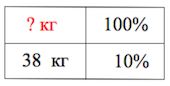
Итак, необходимо взять 380 кг винограда (чтобы получить 40 кг изюма).

Ответ: 380.

^{Задача 43}.

В сосуд, содержащий литров -процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?

В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично - так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .

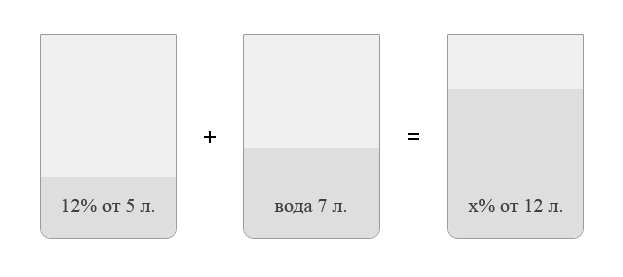
Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:

.

^{Задача 44.}

Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Пусть масса первого раствора равна . Масса второго - тоже . В результате получили раствор массой . Рисуем картинку.

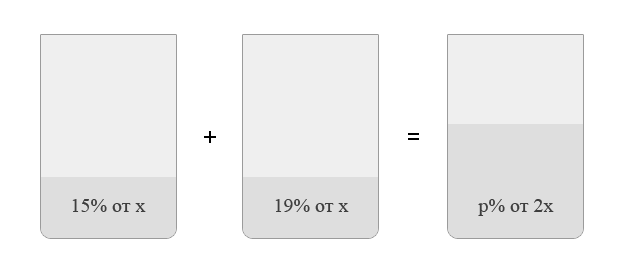
Получаем:

Ответ: .

^{Задача 45.}

Виноград содержит влаги, а изюм - . Сколько килограммов винограда требуется для получения килограммов изюма?

Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог - знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось воды, значит, «сухого вещества» было . В изюме воды и «сухого вещества». Пусть из кг винограда получилось кг изюма. Тогда

от от

Составим уравнение:



и найдем .

Ответ: .

^{Задача 46 .}

Имеется два сплава. Первый сплав содержит никеля, второй - никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий никеля. На сколько килограммов масса первого сплава меньше массы второго?

Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .

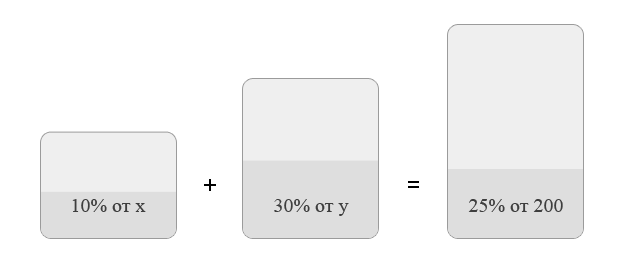
Запишем простую систему уравнений:

Первое уравнение - масса получившегося сплава, второе - масса никеля.

Решая, получим, что .

Ответ: .

Задача 47.

Имеется два раствора серной кислоты в воде: первый -40% , второй-60%процентный.Эти два раствора смешали и добавили 5 кг чистой воды и получили 20%процентный раствор. Если бы вместо чистой воды добавили 5кг 80%процентного раствора, то получили бы 70% процентный раствор. Сколько было 40% и 60% растворов ?

Масса раствора

% содержания

Масса вещества

1 раствор

х

40%

0,4х

2 раствор

у

60%

0,6у

вода

5 кг

0%

0

смесь

Х+у+5

20%

(х+у+5)*0,2=0,4х+0,6у

х=1кг

у=2 кг

Использованная литература

• Копылова Н.П. Решебник «Задачи на смеси и сплавы» 2005г. г.Шелехов.

• Прокопенко Н.И. «Задачи на смеси и сплавы» 2010г. г. Москва

• ЕГЭ Математика 2011 г. ФИПИ-М…Интеллект-Центр,2011.-144с.

• Под редакцией Ф.Ф.Лысенко «Тематические тесты» Издательство «Легион-М»,2010

• Мальцев Д.А., Мальцева Л.И. «Математика. Все для ЕГЭ 2011» 2010г. г.Москва

• www.fipi.ru</</u>