Урок математики в 11 классе

Муниципальное бюджетное образовательное учреждение

«Зеленецкая средняя общеобразовательная школа»

Урок математики в 11 классе

«Логарифмические уравнения»

Учитель математики

Попова Любовь Борисовна

с.Зеленец

2014 г.

«Единственный путь, ведущий к знанию, - это деятельность»

Б.Шоу

Урок математики по теме: Логарифмические уравнения

Учитель математики: Попова Любовь Борисовна

Класс: 11

Автор УМК: Мордкович А.Г.

Тип урока: урок - рефлексия.

Технология: технология развивающего обучения.

Цели урока: создание условий для формирования способностей у учащихся к структурированию и систематизации знаний и умений об основных методах решений логарифмических уравнений.

Задачи: 1. проанализировать индивидуальные затруднения учащихся и выявить их причины;

2. спроектировать выход из создавшихся затруднений;

3. создать учебную ситуацию для устранения причин затруднений решения уравнений;

4. проверить знание формул по теме «Логарифм» и умение применять методы решения логарифмических уравнений.

Оборудование: компьютер, проектор, экран, листы контроля, бумажные кораблики для рефлексии.

Демонстрационный материал: презентация PowerPoint

Ход урока: представлен в таблице. Приложения.

Литература:1.Алгебра и начала анализа. 10-11 класс: учебник для общеобразовательных учреждений / Мордкович А.Г. - М.: Мнемозина, 2013.

2.Алгебра и начала анализа. 10-11 класс: задачник для общеобразовательных учреждений / Мордкович А.Г. - М.: Мнемозина, 2013.

3. Алгебра и начала анализа. 11 класс: Самостоятельные работы для учащихся общеобразовательных учреждений. Л.А.Александрова: под ред. А.Г. Мордковича- М.: Мнемозина, 2013.

4. Алгебра и начала анализа. 10-11 классы. Обучающие контрольные работы. Самсонов И. П.- М.: Илекса, 2011.

Этап урока

Цель

Деятельность учителя

Деятельность учащегося

УУД

1. Организационный

Создать благоприятный настрой на работу.

Подведение

к формулировке темы и цели урока, к постановке задач.

Приветствует учащихся, проверяет их готовность к уроку.

-Какое было домашнее задание?

-Тема урока: Логарифмические уравнения.

(слайд № 1).

-Какую цель и задачи поставим перед собой при проверке домашнего задания и на урок?

(слайд №2)

Приветствуют учителя, проверяют свою готовность к уроку.

Ожидаемый ответ:

-Решить логарифмические уравнения.

Ожидаемый ответ: выявить причины затруднений при решении уравнений дома; выявить пробелы в знаниях и умениях; составить проект выхода из них; повторить формулы.

Личностные:

самоопределение.

Коммуникативные:

планирование учебного сотрудничества.

2.Актуализация знаний

Дать возможность учащимся зафиксировать индивидуальные затруднения при выполнении домашнего задания.

Организует проверку домашнего задания.

Сверяют ответы.

(слайд №3).

Проверяет знание методов решения уравнений через диалог.

- Какие методы решения уравнений знаете? Перечислить.

Предлагает уравнения, решенные дома,

сгруппировать по

методам решения.

(слайд № 4)

Несколько учеников выступают у доски со своими презентациями (приложения 1, 2).

Остальные сопоставляют свои результаты с образцами. Выставляют оценки по выработанным ранее критериям

(приложение 8).

Ожидаемый ответ:

1. По определению (простые).

2. Потенцирование.

3. Введение новой переменной .

4. Функционально-графический.

5.Логарифмирование.

6. Смешанные.

Работают индивидуально, потом результаты обговаривают в парах.

Устно объясняют полученные методы на основе признаков.

Проверяют и оценивают себя.

Личностные:

оценивание усваиваемого материала.

Регулятивные:

познавательная инициатива.

Познавательные:

осознанное и произвольное построение речевого высказывания в устной и письменной форме.

Коммуникативные:

формирование и аргументация своего мнения; учет разных мнений.

3.Постановка проблемы

Выявить и зафиксировать конкретные знания и умения, которых недостает для решения уравнений

Выясняет допущенные ошибки. Выясняет проблемы с помощью подводящего диалога или побуждающего диалога.

Учащиеся анализируют свою домашнюю работу и фиксируют место, шаг, операцию - где возникла ошибка. Выявляют причину затруднения.

Личностные:

смыслообразование.

Регулятивные:

волевая саморегуляция.

Познавательные: постановка и формулирование проблемы.

Коммуникативные:

формулирование и аргументация своего мнения.

4.Устранение затруднений

Выявить причины затруднений и организовать работу по устранению этих причин

Организует выявление причин зафиксированных затруднений и помогает построить проект выхода из затруднений. Предлагает задания для устранения ошибок.

Ставят цели. Выбирают способы достижения цели. Строят план: повторить формулы логарифма и этапы выполнения алгоритма решения уравнений по каждому методу.

Решить подобные уравнения и задания повышенного уровня.

Личностные:

самоопределение.

Регулятивные:

познавательная инициатива

Познавательные:

постановка познавательной цели.

Коммуникативные:

адекватное использование речи для планирования и регуляции своей деятельности

5.Прговаривание причин

Повторить формулы логарифма, основные методы решения уравнений.

Проводит инструктаж работы по повторению формул логарифма.

(приложения 3,4)

Выполняют задания на листах контроля с последующей самопроверкой.

(приложение 4).

Обсуждают допущенные ошибки в записях формул.

Оценивают знание формул по критериям

(приложение8).

Объясняют механизм их использования при решении уравнений.

Личностные:

развитие эстетических чувств и регуляторов морального поведения.

Регулятивные:

контроль, коррекция, волевая саморегуляция.

Познавательные:

использование общих приемов решения.

Коммуникативные:

адекватное использование речи для планирования и реализации своей деятельности.

6.Самоконтроль с самопроверкой

Создать учебную ситуацию для практического применения методов решения уравнений.

Предлагает выполнить самостоятельную работу. Ставит задачу: определить методы решения уравнений и решить их.

(слайды №5, №6)

Работают в тетрадях.

Выбирают уравнения для решения по уровням.

I - уровень 1а,2а,3а,4а.

II - уровень 1b,2b,3b,4b.

III - повышенный уровень .

По окончании сверяют решение и оценивают свою работу по критериям

(приложение 8)

Личностные:

развитие морального поведения.

Регулятивные:

волевая саморегуляция.

Познавательные: анализ, сравнение.

Коммуникативные:

адекватное использование речи для планирования и регуляции своей деятельности.

7.Информция

о домашнем задании

Обеспечение понимания учащимися стратегии выполнения домашней работы

Предлагает

найти и решить логарифмические уравнения из КИМов.

Записывают домашнее задание. Задают вопросы

Личностные:

формирование навыков самоконтроля

Регулятивные:

составление плана выполнения работы.

Познавательные:

поиск необходимой информации.

Коммуникативные:

умение выслушивать

8.Рефлексия

Дать возможность проанализировать и оценить свою работу каждому ученику. Соотнести поставленные задачи с достигнутым результатом. Обеспечить позитивный настрой

Задает вопросы о достижении поставленных задач на уроке.

Предлагает отразить свои достижения на графике функции

у = log_ax.

(слайд № 7 )

- Постройте графики функции у = log_ax при 0 < a < 1 и при а > 1. Поставьте свою бумажную лодочку на том графике, которое отражает ваши ощущения на уроке: чувствовали ли вы рост или наоборот, падение, и на каком уровне.

Обеспечивает положительную

реакцию учащихся.

Анализируют и оценивают свою работу.

Получают позитивный настрой от урока.

Личностные:

самооценка на основе критерия успешности.

Регулятивные:

осознание уровня и качества усвоения знаний и умений.

Познавательные:

контроль и оценка процесса и результатов деятельности.

Коммуникативные:

формирование и аргументация своего мнения.

Приложение 1.

1.Домашняя работа

Решить данные логарифмические уравнения.

1. log₁₃ (x - 4) = 1

2. log₅ (2x+3) = log₅ (x +5)

3. 17 ^log₁₇^(5X-2) = 8

4. log₂₉ (4 - 5x) = log₂₉ 3 + log₂₉ 4

5. log₇ 36 - log₇ (3x - 12) = log₇ 4

6. 9log ₃ x - x²log₃ x = 0

7. log_⅓ (2x - 5) =

8.

9. (log₂ x + 2 log _x 2) (log₂ x - 2 log _x 2) = 3

10. 2log ²₄ x - log₄ x¹³ = 7

11. x^1+log₃^x = 9

Приложение 2. Выступления учащихся(в виде презентаций).

1. log₁₃ (x - 4) = 1

x - 4 =13 ОДЗ: x - 4 > 0

x = 17 x > 4

Ответ: 17

2. log₅ (2x+3) = log₅ (x +5)

(2x+3) = (x +5) ОДЗ: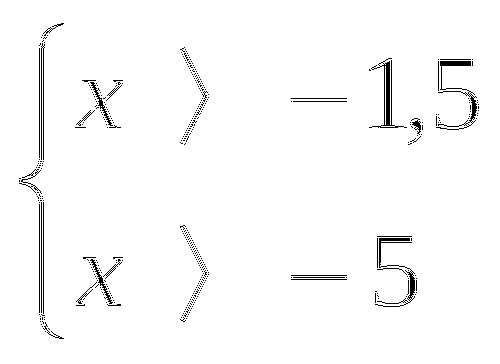x > -1, 5

x = 2

Ответ: 2

3. 17 ^log₁₇^(5X-2) = 8

(5x - 2) = 8 ОДЗ: 5 x - 2 > 0

5x = 10 x > 0,4

x = 2

Ответ: 2

4. log₂₉ (4 - 5x) = log₂₉ 3 + log₂₉ 4

log₂₉ (4 - 5x) = log₂₉ 12

4 - 5x = 12 ОДЗ: 4- 5 x > 0

x = -1,6 x<0,8

Ответ: -1,6

5. log₇ 36 - log₇ (3x - 12) = log₇ 4

log₇ = log₇ 4

= 4

4(3x-12) = 36 ОДЗ: 3 x - 12 > 0

12x-48 = 36 x > 4

12x = 84

x = 7

Ответ: 7

6. 9log ₃ x - x²log₃ x = 0 ОДЗ: x > 0

Пусть log₃ x = t

9 t - x²t = 0

t (9 - x²) = 0

t = 0 или 9 - x² = 0

log ₃ x = 0 x² = 9

x = 1 x_1;2 = ± 3

Ответ: 1; 3

7. log_⅓ (2x - 5) =

y₁ = log_⅓ (2x - 5) убывающая на D є (2,5;+∞)

y₂ = возрастающая на D є [3 ;+∞)

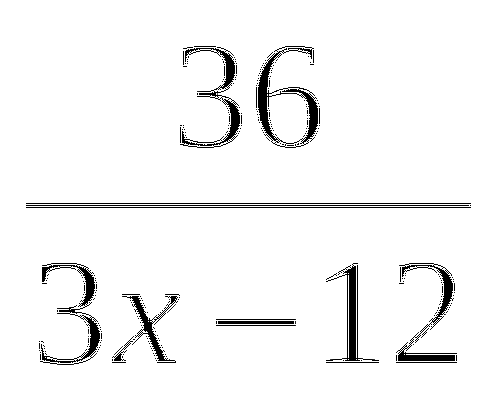
x =2,5Ответ: 3

8.

log ²₃ x - 4log₃x + 3 = 0 log₃(x - 5) ≠ 0

Пусть log₃ x = t (x - 5) ≠ 3⁰

t² - 4t + 3 = 0 x -5 ≠ 1

D = 4 x ≠ 6

t_1;2 = 1;3

log ₃ x = 1 log₃ x = 3 ОДЗ: x - 5 > 0

x = 2 x = 27 x > 5

Ответ: 27

9. (log₂ x + 2 log _x 2) (log₂ x - 2 log _x 2) = 3

(log₂ x + 2 ) (log₂ x - 2 ) = 3 ОДЗ: x > 0 , х ≠ 1

Пусть log₂ x = t

(t + 2 ) (t - 2 ) = 3

(t² - 4 ) = 3

t ⁴ - 4 - 3t ² = 0

Пусть t² = z

z ² - 4 - 3z= 0

D = 25

z_1;2 = -1; 4

t² = -1 t² = 4

нет решений t_1;2 = ±2

log ₂ x = - 2 log₂ x = 2

x = 2^-2 x = 2²

x = 0,25 x = 4

Ответ: 0,25; 4

10. 2log ²₄ x - log₄ x¹³ = 7

2log ²₄ x - 13 log ₄ x = 7 ОДЗ: x > 0

Пусть log₄ x = t

2 t² - 13t - 7 = 0

D = 225

t_1;2 = -0,5; 7

log ₄ x = - 0,5 log₄ x = 7

x = 4^-0,5 x = 4⁷

x = 0,5 x = 16384

Ответ: 0,5; 16384

11. x^1+log₃^x = 9

log₃ x^1+log₃^x = log₃ 9 ОДЗ: x > 0

(1 + log₃ x ) log₃ x = 2

log ₃ x + (log₃ x) ² - 2 = 0

Пусть log₃ x = t

t + t² - 2 =0

D = 9

t_1;2 = -2; 1

log ₃ x = - 2 log₃ x = 1

x = 3^-2 x = 3

x = 1/9

Ответ: 1/9; 3

Приложение 3. Формулы по теме «Логарифм»

вопрос

ответ

Оценка

(+ верно,

! ошибся)

? не знаю

1. Определение логарифма

Логарифмом числа b по основанию a называется такое число, обозначаемое log _a b

2. Обозначение десятичного логарифма

3. Обозначение натурального логарифма

где e = 2,7

4. Основные логарифмические тождества

5. Логарифм 1 при любом основании (формула)

6. Когда логарифм равен 1 (формула)

7. Логарифм произведения двух неотрицательных чисел (формула)

8. Логарифм частного (формула)

9. Логарифм степени(формула)

10. Формула перехода к новому основанию логарифма

11.Следствия из формулы перехода к новому основанию логарифма

12.Логарифм корня (формула)

Приложение 4. Лист контроля

вопрос

ответ

Оценка

(+ верно,

! ошибся)

? не знаю

1.Определение логарифма

2.Обозначение десятичного логарифма

3.Обозначение натурального логарифма

4.основные логарифмические тождества

5.Логарифм 1 при любом основании (формула)

6.Когда логарифм равен 1 (формула)

7.Логарифм произведения двух неотрицательных чисел (формула)

8.Логарифм частного (формула)

9 Логарифм степени (формула)

10.Формула перехода к новому основанию логарифма

11. Следствия из формулы перехода к новому основанию логарифма

12.Логарифм корня (формула)

Приложение 5.Самостоятельная работа.

1. a) log5 (8 - 24x) - log5 8 = log57

b) lg (x + 3) = 2 lg 2 - lg x

2. a) log6 (x² + 5x) = 1

b) log2 (x -3) + log2(x -2) = 1

3. a) lg x = 11 - x

b) log2 x = - 0,5 - x

4. a) 3log²8x + 5 log8x = 2

b) 2 log3x + 1 4 - log2 (3x + 1) + 3 = 0

Ответы:

1а) -2. 2а) -6; 2 3а) 10 4а) 1/64; 2

1b) 1 2 b) 4 3 b) 0,5 4 b) -1/6 ; 5

Приложение 6.Задания повышенного уровня.

1. log8x log9x log7x+6[(7x+6)9 +x² -x -56] =0

2. 0,5 log1,3 (16 -5x ) - log1,3(2x -5) =0

Ответы: 1. 8 2. 3

Приложение 7. График логарифмической функции.

у = log_ax

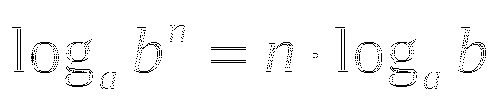
Приложение 8. Критерии оценивания

Домашней работы: решено 11 уравнений - «5»

решено 8 -10 уравнений - «4»

решено 5-7 уравнений - «4»

Знание формул: все 12 формул -«5»

10-11 формул -«4»

7-8 формул -«3»

Самостоятельной работы: решено 4 уравнения - «5»

решено 3 уравнения - «4»

решено 2 уравнения - «3»

Конспект урока

Тема: «Площадь криволинейной трапеции»

Цели:

1. Воспитательные:

   1. воспитание положительного отношения к знаниям;

   2. воспитание дисциплинированности;

   3. воспитание эстетических взглядов.

2. Развивающие:

   1. развитие психических качеств студентов: мышления, умений применять полученные знания на практике;

   2. развитие познавательных умений (выделять главное, вести конспект);

   3. развитие общетрудовых и политехнических умений;

   4. развитие умений учебного труда (читать, писать);

   5. развитие воли, самостоятельности).

3. Образовательные:

   1. закрепить навыки нахождения определенного интеграла;

   2. добиться усвоения студентами понятия «криволинейная трапеция»;

   3. обеспечить усвоение студентами различных способов нахождения площади криволинейной трапеции;

   4. отработать навыки нахождения площади криволинейной трапеции.

Тип: комбинированный

Оборудование: Компьютерный класс, интерактивная доска, проектор, карточки-задания.

Демонстрационный материал: презентация PowerPoint, файлы для работы с интерактивной доской (ИД).

План урока

I. Самоопределение к деятельности (оргмомент) - 3 мин.

II. Актуализация опорных знаний - 10 мин.

III. «Открытие» новых знаний - 10 мин.

IV. Применение знаний, формирование умений - 20 мин.

V. Подведение итогов, домашнее задание - 2 мин.

ХОД УРОКА:

I. Самоопределение к деятельности

Здравствуйте, садитесь. Дежурный, кто сегодня отсутствует?

Тема нашего урока «Площадь криволинейной трапеции».

Вы знакомы с понятием «определенный интеграл» и научились его вычислять.

Сегодня мы сформулируем понятие «криволинейная трапеция» и научимся вычислять ее площадь с помощью определенного интеграла.

II. Актуализация опорных знаний

Вспомним материал предыдущих уроков по теме «Определенный интеграл».

Для проведения контроля нам необходимо назначить консультанта. Есть желающие? Консультант выставит оценки за компьютерное тестирование. Напоминаю, оценка «5» ставится за 90-100% правильных ответов, «4» - 70-90%, «3» - 60-70%, «3» - 50-70%, будем надеется, что меньше 50% никто не наберет.

При работе за компьютером необходимо помнить правила по технике безопасности.

Кто желает пройти компьютерное тестирование? - 10 человек.

Пока ребята отвечают на вопросы теста, мы ответим на вопросы у доски.

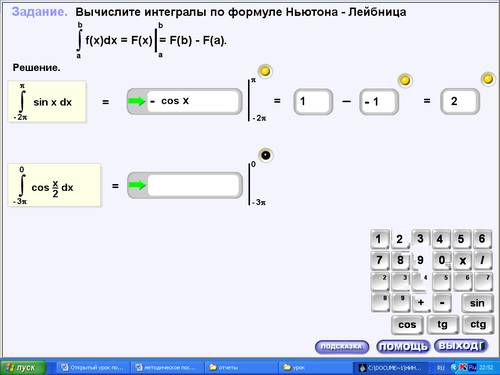
1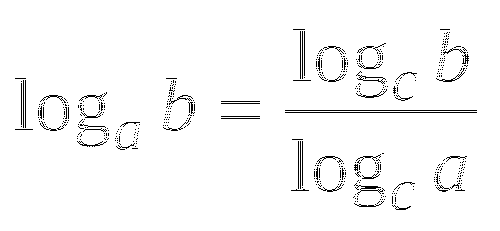. Записать формулу Ньютона-Лейбница.

А теперь примени ее для нахождения определенного интеграла.

(14.ехе, задание 1, пример 1)

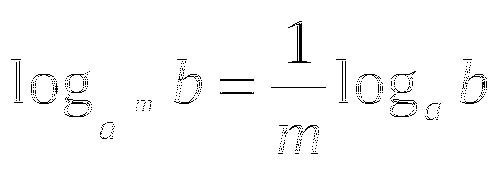
2. Что такое определенный интеграл?

Здесь тоже фигурирует формула Ньютона-Лейбница. Найди определенный интеграл по этой формуле. (14.ехе, задание 1, пример 2)

Формула Ньютона-Лейбница… Откуда взялась эта формула. Вам было дано домашнее задание найти историческую справку. Кто нам об этом расскажет? (Историческая справка, слайд 1)

(Консультант выставляет оценки студентам).

3. В чем заключается геометрический смысл определенного интеграла?

III. «Открытие» новых знаний

1) И так, определенный интеграл - это площадь фигуры, ограниченной графиком положительной функции f(х), осью абсцисс и прямыми х=а, х=в. Такая фигура называется криволинейной трапецией.

Сегодня мы узнаем, что такое криволинейная трапеция и рассмотрим различные способы нахождения ее площади с помощью определенного интеграла.

Запишите в тетрадях тему урока: «Площадь криволинейной трапеции» (слайд 2).

2) Что же такое криволинейная трапеция?

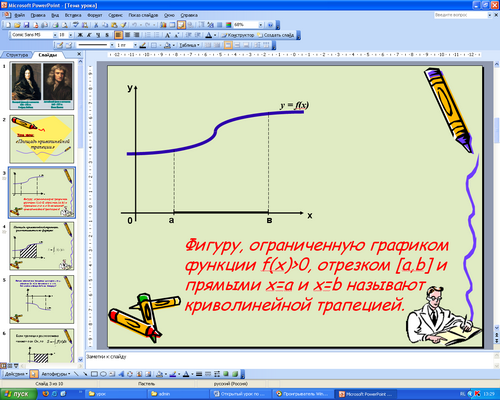
Пусть на отрезке [a; b] оси абсцисс определена функция у=f(х)>0. Фигура, ограниченная графиком этой функции, отрезком [a; b] и прямыми х=а, х=b называется криволинейной трапецией (слайд 3). В тетрадях сделайте чертеж и запишите определение.

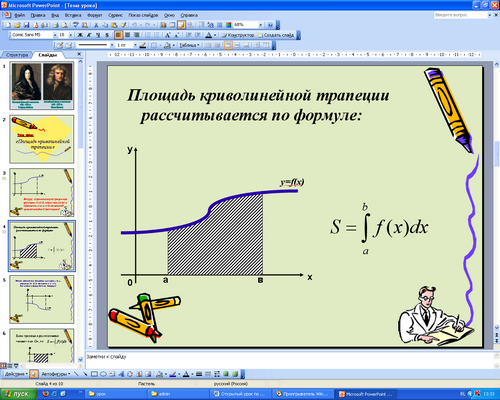
3) Исходя из геометрического смысла определенного интеграла, площадь криволинейной трапеции равна: (слайд 4), где пределы интегрирования - это отрезок [a; b] оси абсцисс, на котором мы рассматриваем трапецию, а подинтегральная функция - та, график которой ограничивает трапецию сверху.

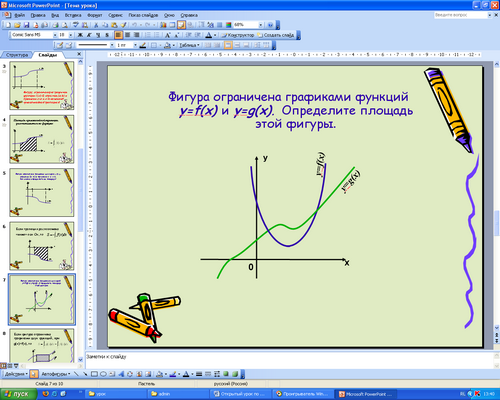
4) Рассмотрим следующие фигуры.

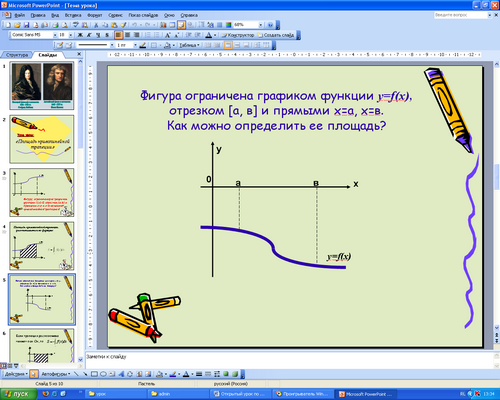
а) (слайд 5). Фигура ограничена графиком функции у=f(x), отрезком [a, в] и прямыми х=а, х=в. Заштрихуйте фигуру, ограниченную этими линиями.

Как можно определить площадь этой фигуры? (Проинтегрировать функцию у=f(x) на отрезке [a, в]).

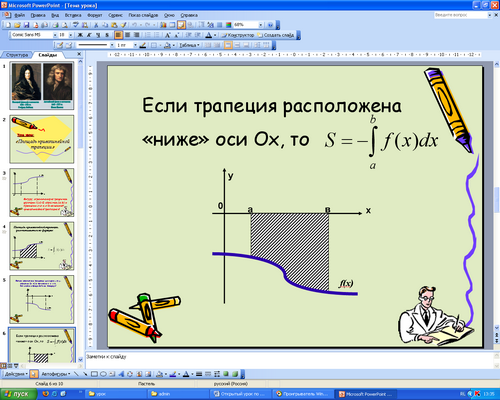
Но эта фигура находится «ниже» оси Ох и вычисляя интеграл мы получим отрицательное значение, чего не может быть при вычислении площади.

Следовательно, площадь равна: (прописать).

Запишите в тетрадях правило нахождения площади рассмотренной фигуры. (слайд 6)

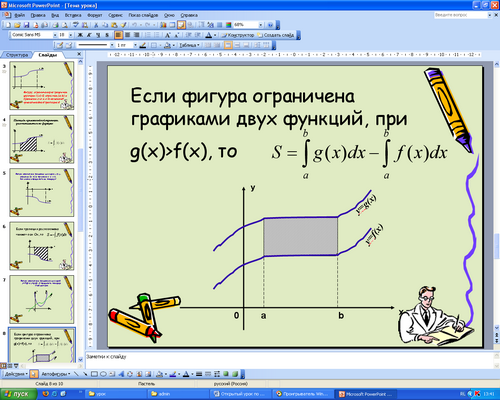
б) (слайд 7). Покажите криволинейную трапецию, ограниченную графиками функций g(x) и f(x).

На каком отрезке рассматривается данная фигура?

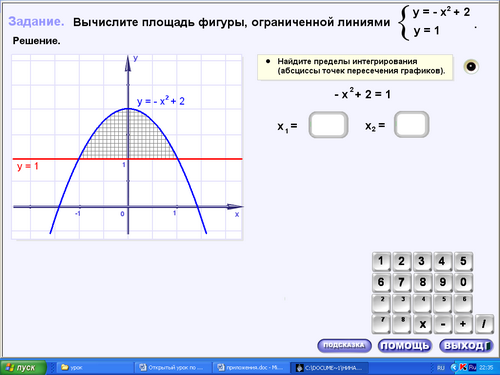
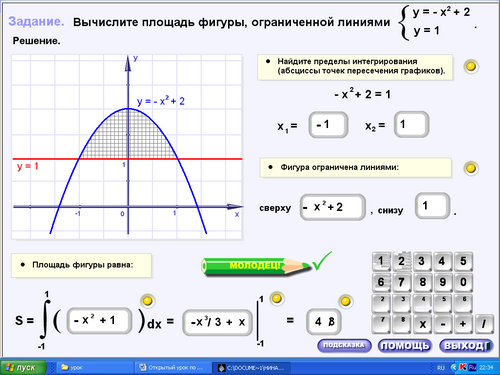
Как найти концы этого отрезка? (Концы отрезка - это точки пересечения графиков. Чтобы найти абсциссы этих точек функции надо приравнять).

А как вычислить площадь этой фигуры? (Эта фигура является разностью фигур с площадями S₁ и S₂).

Следовательно, S=S₁-S₂ (прописать).

Запишите в тетрадях правило нахождения площади рассмотренной фигуры. (слайд 8)

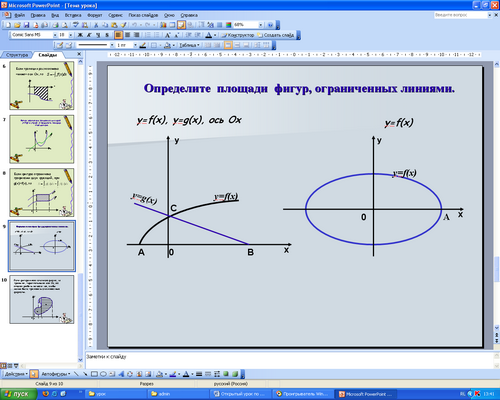
в) (слайд 9). Заштрихуйте фигуру, ограниченную графиками функций g(x) и f(x) и осью абсцисс.

В чем особенность этой фигуры? (Она состоит из двух частей, одна сверху ограничена графиком функции f(x) и рассматривается на отрезке [А,0], другая - графиком g(x) на отрезке[0, В]).

Следовательно, S=S₁+S₂ (прописать).

г) Заштрихуем фигуру, ограниченную графиком функции f(x). Эта фигура состоит из 4-х одинаковых фигур. Если проинтегрировать функцию у=f(x) на отрезке [0; A] и умножить на 4, то получим искомую площадь.

Следовательно, S = 4S₁ (прописать).

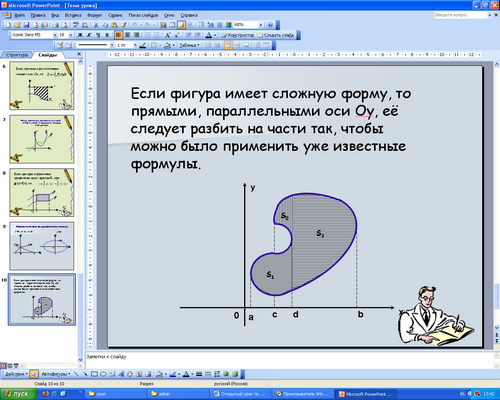
Запишите в тетрадях правило нахождения площади рассмотренных фигур. (слайд 10)

IV. Применение знаний, формирование умений

1) А теперь применим полученные знания на практике.

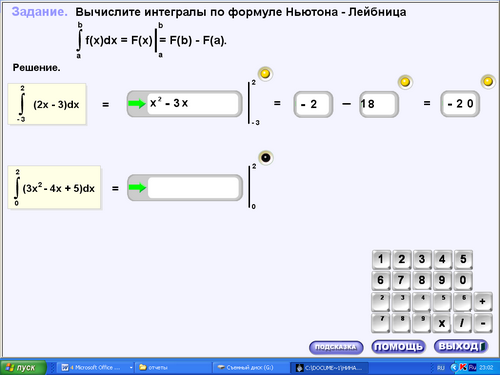
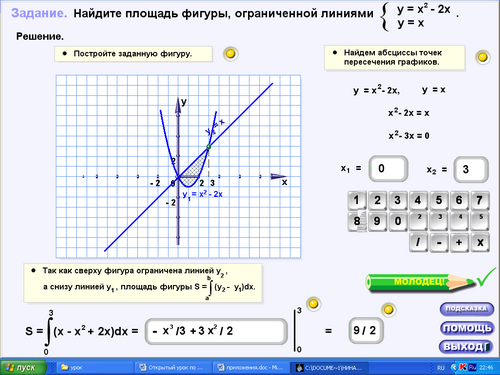
Решим задачу вместе со мной. (15.ехе, практика, задача 2). Для определения площади фигуры построим эту фигуру.

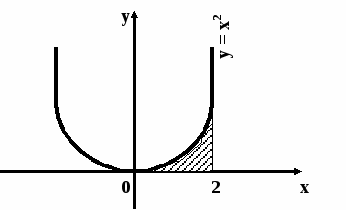
Найдем точки, в которых графики пересекаются, для этого приравняем функции, получаем уравнение х² - 3х = 0. Отсюда следует, что х₁ = 0, х₁ =3.

Графиком функции у = х² - 2х является парабола, ветви вверх, пересекает ось Ох в точках 0 и 2. График функции у = х - прямая. Построим эти графики. Получили ограниченную этими графиками фигуру. Так как сверху фигура ограничена графиком у = х, снизу - у = х² - 2х, то искомая площадь вычисляется как разность интегралов: , по свойству интегралов получаем: . Приведем подобные, получаем под-интегральную функцию - х² + 3х. Находим первообразную: - х³ /3 + 3х² /2.

Подставим верхний предел интегрирования:

(прописать)

Я молодец!

2) Посмотрим, как получится у вас.

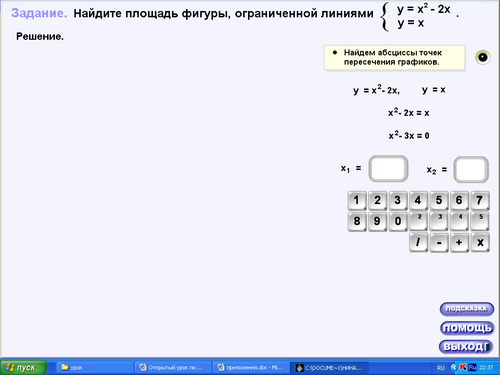
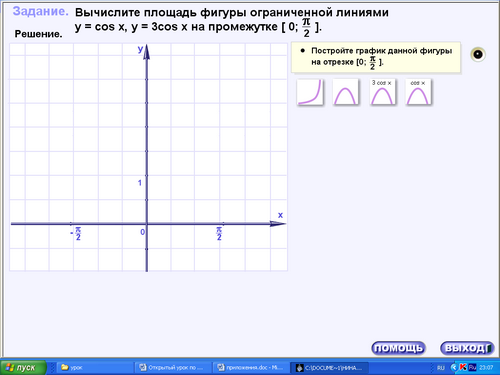
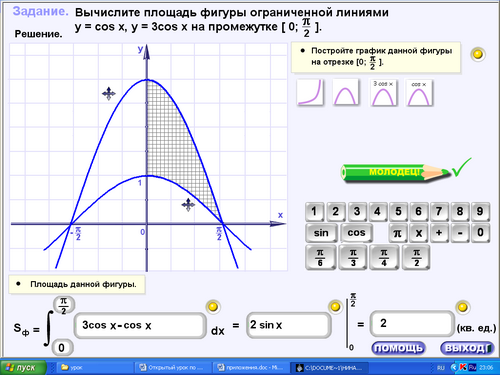
а) (15.ехе, практика, задача 1) Прочитать условие. Кто желает решить задачу у доски?

б) (16.ехе, практика, задача 3) Прочитать условие. Кто желает решить задачу у доски?

3) Сегодня мы познакомились с понятием «криволинейная трапеция», узнали, как можно вычислять ее площадь.

А теперь посмотрим, как вы разобрались в этом материале (Самостоятельная работа)

V. Подведение итогов, домашнее задание

Собрать выполненные самостоятельные работы.

Кто выполнял задание на «5», кто - на «4», кто - на «3»? Оценки за самостоятельную работу вы узнаете на следующем уроке, а сегодня на уроке получили оценки:

а) тест - 10 чел.

б) за ответ у доски - 3 чел.

в) за решение примеров - 2 чел.

Д/З: гл.13, §1, №12,13

Дополнительное задание:

Найти в Интернет примеры практического применения вычисления площади криволинейной трапеции.

Приложение 1

САМОАНАЛИЗ

Урок по теме «Площадь криволинейной трапеции» изучается в конце раздела «Интегрирование», после темы «Определенный интеграл» и является ее логическим продолжением. Для усвоения данной темы студенты должны хорошо владеть понятием «Определенный интеграл» и уметь находиться его, используя формулу Ньютона-Лейбница. После темы «Площадь криволинейной трапеции» изучается тема «Объемы тел», которая является заключительной в данном разделе.

Цели урока:

1. Образовательные:

а) закрепить навыки нахождения определенного интеграла;

б) обеспечить усвоение студентами понятия «криволинейная трапеция» и различных способов нахождения площади криволинейной трапеции;

в) сформировать навыки нахождения площади криволинейной трапеции путем вычитания площадей.

2. Развивающие:

а) развивать психических качеств студентов (умений применять полученные знания на практике);

б) развивать познавательных умений и мышления (выделять главное, анализировать, сравнивать, определять и объяснять понятия).

3. Воспитательные:

а) воспитывать положительного отношения к знаниям;

б) воспитывать дисциплинированности.

Тип урока: комбинированный.

Особенностью данного урока является применение информационно-коммуникационных технологий.

При проверке знаний по теме «Определенный интеграл» используется машинный программированный контроль, который позволяет за относительно небольшой промежуток времени проверить качество знаний большого числа студентов, в данном случае это 10 учеников.

При изучении нового материала используется презентация PowerPoint с элементами мультимедиа.

Использование интерактивной доски на этом этапе урока позволяет сократить время на построение графиков, запись формул и определений. Материал становится более наглядным и более доступным.

Бòльшая часть урока отводится на закрепление полученных теоретических знаний. Закрепление материала заключается в решении задач из электронного учебного пособия.

При выполнении домашнего задания студенты будут использовать ресурсы сети Интернет, что одновременно способствует совершенствованию навыков работы с цифровыми образовательными ресурсами и повышает интерес к предмету, а, следовательно, способствует совершенствованию достижений навыков образовательных результатов.

Ожидаемые результаты

• Сформированные знания понятия «криволинейная трапеция», формулы площади криволинейной трапеции, способов нахождения площадей различных фигур.

• Сформированные навыки применения определенного интеграла к вычислению площади криволинейной трапеции путем вычитания площадей.

Цели - это конечный результат. На мой взгляд, цели и ожидаемый результат совпали.

Приложение 2

Вопросы машинного программированного контроля

1. Чему равен нижний предел интегрирования в интеграле 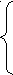(-2)

2. Данный интеграл 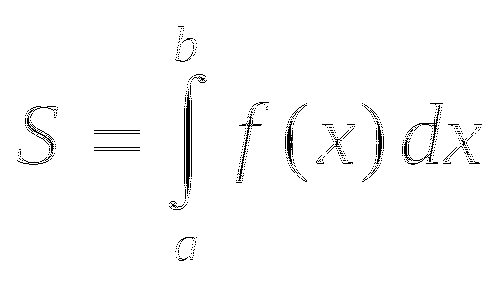равен:

а) 0

б) -4

в) 4

г) 8

3. В данном интеграле 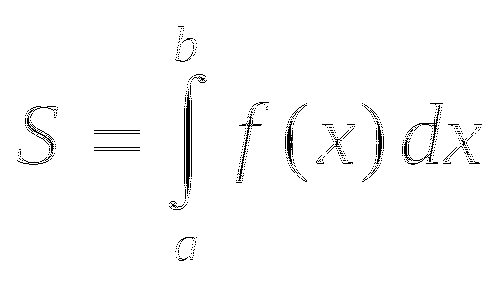подинтегральная функция равна:

а) 2х

б) dх

в) 0

г) 2

4. Данный интеграл 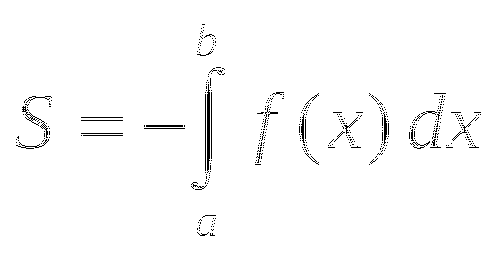равен:

а) 1

б) С

в) 0

г) зависит от подинтегральной функции

5. Выражение данного вида 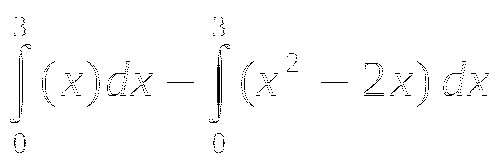называется:

а) определенный интеграл

б) неопределенный интеграл

в) интегралом функции

г) дифференциалом

6. Определенный интеграл вычисляется с помощью формулы:

а) Лейбница

б) Ньютона

в) Лагранжа

г) Ньютона-Лейбница

7. При перестановке пределов интегрирования в определенном интеграле, интеграл ...

а) не изменится

б) увеличится в 2 раза

в) поменяет знак

г) подинтегральная функция изменится на обратную

Приложение 3

Приложение 4

Приложение 5

Самостоятельная работа

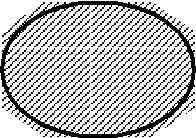
1. Н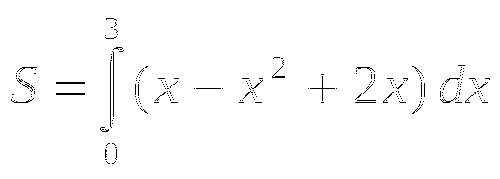айдите площадь криволинейной трапеции, изображенной на рисунке:

2. Н

   yайдите площадь фигуры, изображенной на рисунке:

0

у = sin x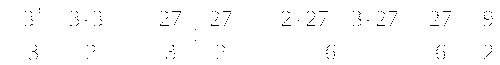

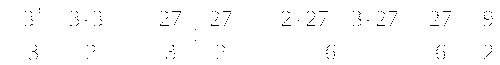
х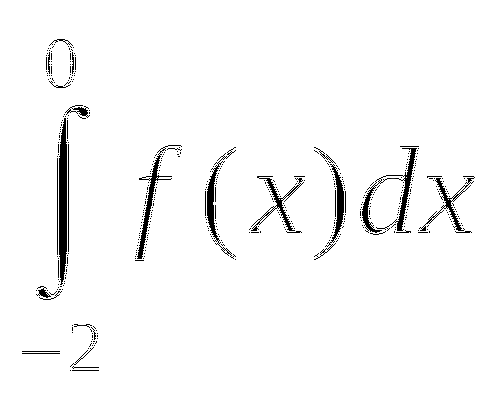

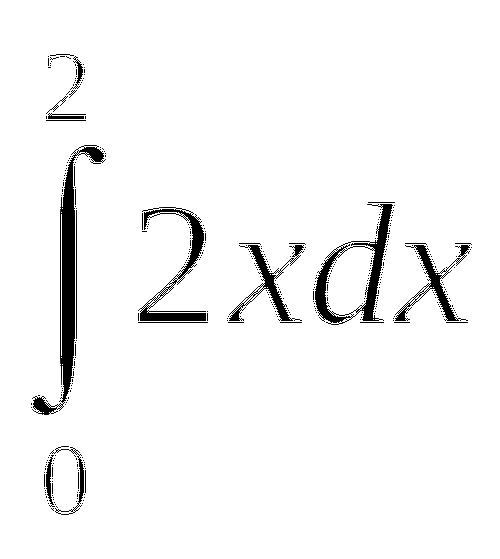
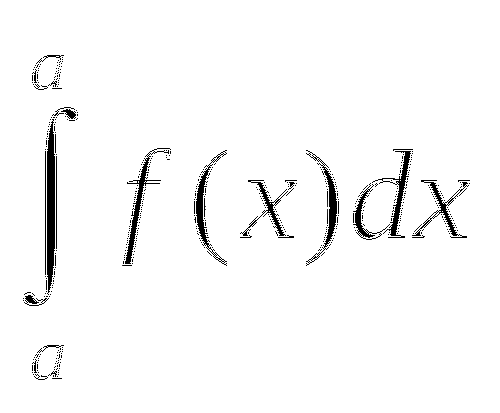
0

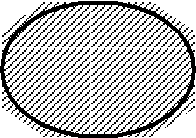
3. Н

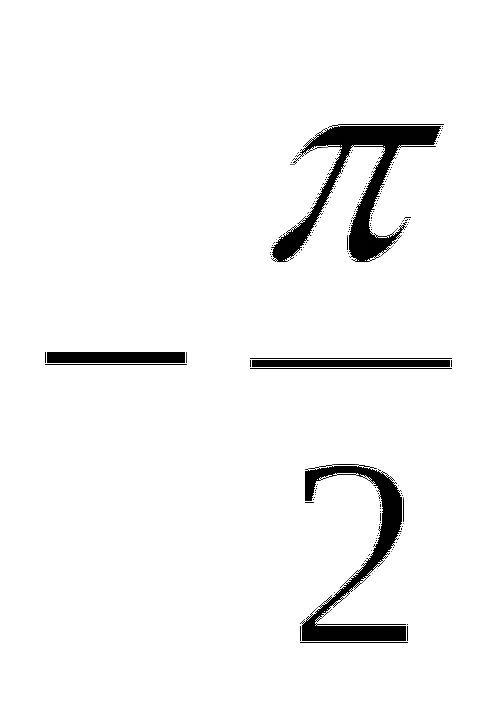
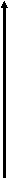
   х

   yайдите площадь фигуры, ограниченной прямой и параболой

Оценка «3» ставится за правильное решение задания №1

Оценка «4» ставится за правильное решение задания №2

Оценка «5» ставится за правильное решение задания №3

Материалы для посещающего урок

Основные критерии эффективности

применения ИКТ на уроке

Безусловно, что умелое сочетание традиционных и информационных средств зависит от квалификации и мастерства преподавателя, методики, которую он применяет. Но грамотное использование средств ИТ зависит и от знаний преподавателем педагогических основ по информатизации уроков.

Основные критерии эффективности применения ИКТ на отдельных этапах уро­ка следующие:

• целесообразность;

• соблюдение санитарных норм;

• соблюдение баланса между средствами ИКТ и средствами человеческо­го общения;

• соответствие материала на ЦОРе возрастным особенностям обучающихся;

• четкость инструктажа каждого задания;

• активность обучающихся;

• ощущение комфортности;

• рефлексия.

Все эти критерии должен учитывать преподаватель при составлении урока, а завуч должен обратить внимание насколько успешно преподаватель руководствуется этими критериями.

ТИПОВАЯ КАРТА ПОСЕЩЕНИЯ УРОКА

Дата посещения

Преподаватель

Предмет

Группа

Классный руководитель

На уроке присутствовали:

1. Общая информация об уроке

1.1. Причина посещения урока (отмечается одна из причин)

• плановое посещение;

• внеплановое посещение (указывается причина внепланового посещения).

1. 2. Цель посещения урока (отмечается одна из целей)

• знакомство с преподавателем;

• комплексное наблюдение за работой преподавателя;

• наблюдение за работой преподавателя в связи с определенной проблемой или ре­шением определенной задачи (указывается проблема или задача)

• наблюдение за работой класса, отдельных обучающийся;

• диагностика затруднений преподавателя;

• диагностика затруднений группы;

• контроль (указывается форма контроля),

• подготовка к аттестации;

• аттестация;

• психолого-педагогическое наблюдение;

• другое (указывается цель посещения).

1. 3. Общая характеристика урока
1.3.1 .Тема урока: ___________________________________

1.3.2. Место урока в системе уроков .

1.3.3. Тип урока .

1.3.4. Цель урока .

1.3.5. задачи урока .

1.3.6. оборудование и наглядные пособия, использованные на уроке (в том числе использование доски)

1.3.7. Контроль и оценивание умений, знаний и навыков обучающихся

1.3.8. Работа с тетрадями обучающийся ______

2. Краткий конспект урока с комментариями,

замечаниями, рекомендациями

Этап урока,

его краткое содержание

Деятельность учащихся

Деятельность преподавателя

Комментарии, замечания, рекомендации

3. Анализ урока

3.1. Исчерпанность темы

- исчерпана полностью; - исчерпана не полностью;

- практически не исчерпана; - не исчерпана.

Замечания, рекомендации ___________________________________________

____________________________________________________________________________________________________________________________________

3.2. Степень реализации цели урока

• цель реализована;

• цель реализована не полностью;

• цель не реализована.

3.3. Степень выполнения задач

- задачи выполнены полностью; - все задачи выполнены частично

- выполнены не все задачи; - задачи не выполнены.

Замечания, рекомендации ____________________________________________

__________________________________________________________________

3.4. Характер отбора содержания материала урока

- научность, значимость теорети- - привлекательность;

ческая; - дифференцированность;

- значимость практическая; - логичность;

- доступность; - наглядность;

- соответствие возрастным и ин- - другое (указать, что),

теллектуальным возможностям

обучающихся;

3.5. Характеристика форм работы

- соответствие цели, задачам и - сменяемость;

содержанию; - другое (указать, что).

- разнообразие;

- чередуемость;

3.6. Логичность композиции урока

• композиция урока логична;

• композиционная логика отсутствует.

• в композиции урока имеются нарушения логики;

Замечания, рекомендации

_________________________________________________________________

3.7. Развивающая характеристика урока, развитие устной речи школьников

3.8. Психологическая характеристика урока (психологический климат заня­тия)

Параметры оценки

+

+/-

-

?

Разнообразие приемов психологического воздействия и стимулирования активности обучающихся

Разумное соотношение нагрузки на память и мышление

Разумное соотношение воспроизводящей и творческой деятельности

Разумное соотношение знаний «в готовом виде» и их самостоятельного поиска

Разумное соотношение побуждения обучающихся к деятельности и корректного принуждения школьников

Педагогический такт преподавателя

Психологический климат в классе

Рабочее самочувствие преподавателя на уроке самочувствие обучающихся на уроке

Учет возрастных и психофизических особенностей отдельных обучающихся и класса в целом

Другое

Примерная схема анализа урока с использованием

информационно - коммуникационных технологий

3.9 Анализ эффективности использования средств ИКТ

+

+/-

-

?

Актуальность использования средств ИКТ

Вид используемых на уроке средств ИКТ

• презентация в PowerPoint

• электронные учебные издания (ЭУИ)

• ресурсы сети Интернет

• цифровые лаборатории

3.9.1 Презентация
Текстовое оформление

- Структура - Формат

- Объем - Подача текстовой информации

Эстетика оформления слайдов

- Цветовая гамма - Анимация

- Звуковое сопровождение

Видеоинформация

- Время - Обратная связь

3.9.2 Цифровые образовательные ресурсы (ЦОР)

ЭУИ

- Соответствие возрастным осо- - Дружественный интерфейс

бенностям учащегося

- Удобная навигация

Интернет

Соответствие теме урока

Соответствие возрастным особенностям обучающихся

Достоверность информации

Поиск инфор-мации в WWW

Тестирование

on-line

Виртуальные

экскурсии

3.9.3 Соблюдение санитарно-гигиенических требований

4. Анализ домашнего задания

По объему

По содержанию

По форме

Примечания, замечания

• соответствует нормам;

• перегруженное;

• недостаточное;

• только на ближайший урок;

• несколько уроков вперед;

• всю тему (блок, раздел).

• только репродуктивное;

• только продуктивное;

• продуктивное + репродуктивное;

• связано только с пройденным материалом;

• перспективное;

• связывает пройденный материал с материалом следующих уроков;

• не связано с материалом следующих уроков.

• только устное;

• только письменное;

• устное + письменное;

• одинаковое для всех обучающихся;

• дифференцированное по сложности;

• дифференцированное представлен выбор самим обучающимся);

• с индивидуальными и групповыми заданиями.

5. Оценка урока

1. Оценка урока учителем (самооценка)

2. Замечания и предложения

Заключение

Анализ любого урока представляет собой комплексный подход, в кото­ром психологический, педагогический, содержательный, методический и пред­метный аспекты тесно взаимосвязаны. Сам по себе анализ урока как процесс осознания и самопознания формирует у учителя аналитические способности, развивает интерес и определяет необходимость изучения проблем обучения и воспитания. Умение проводить наблюдения за сложными педагогическими яв­лениями, анализировать их, обобщать и делать научно обоснованные выводы, служит действенным средством совершенствования профессионально-педагогического мастерства.