Урок по геометрии по теме Осевая и центральная симметрия

Конспект урока по геометрии в 8 класса

Проводящий: Попова Елена Григорьевна

Дата проведения: 12.10.16 г.

Место проведения: кабинет №8.

Тип урока: изучение нового материала.

Тема: «Осевая и центральная симметрии»

Образовательная цель: создать условия для формирования понятия «симметрия», изучить основные виды симметрии на плоскости

Задачи: формирование УУД:

познавательные: познакомить с понятиями осевой и центральной симметрии; учить строить геометрические фигуры симметричные относительно прямой и центра симметрии; решать задачи; перерабатывать полученную информацию, наблюдать и делать самостоятельно делать выводы.

регулятивные: закреплять умения контролировать и корректировать свою деятельность самостоятельно выполнять предложенные задания;

личностные и коммуникативные: формировать умение работать в паре, слушать и понимать речь других, вступать на уроке в беседу, развитие внимания, памяти, логического и творческого мышления содействовать воспитанию интереса к математике, активности.

Форма работы: фронтальная, работа в парах, индивидуальная.

Оборудование: компьютер, проектор, учебник математики, карточки, электронная презентация, выполненная

в программе PowerPoint.

Структура и ход урока:

Технологическая карта урока

Этапы урока

Деятельность учителя

Деятельность ученика

УУД

1.

Организационный этап. (2 минуты)

Задачи:Подготовить учащихся к работе на уроке. Создать благоприятный психологический настрой на работу.

Учитель приветствует обучающихся, проверяет готовность к уроку. С помощью стихотворения учитель создаёт условия для положительного настроя учащихся на дальнейшую деятельность.

Древняя китайская мудрость гласит:

«Я слышу - я забываю,

Я вижу - я запоминаю,

Я делаю - я понимаю».

Сегодня я на уроке предлагаю работать, следуя совету китайских мудрецов: «Я слышу - я вижу - я делаю»

- учитель прветствует учащихся;

- организует внимание;

- проверяет готовность класса;

- создаёт условия для положительного настроя учащихся на дальнейшую деятельность;

- приветствуют учителя;

- настраиваются на урок, включаясь в деловой ритм урока.

Личностные: умение выделять нравственный аспект поведения, самоопределение.

Регулятивые: целеполагание и планирование учебного сотрудничества с учителем и сверстниками.

Познаватнльные:

умение ориентироваться в собственной системе знаний.

Коммуникативные:

умение слушать и понимать речь других.

2.

Проверка знаний. Актуализация опорных знаний. (7 минут)

Задача: организовать познавательную деятельность учащихся.

Устная работа, с помощью которой ведется повторение основных фактов, ведущих идей и основных теорий на основе систематизации знаний.

Что мы изучали на прошлых уроках «Четырехугольники» их свойства.

Слайд№1

1.Решите задачи (устно)

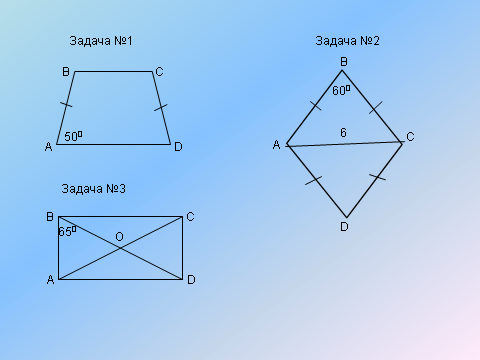Ответы: №1 130⁰, 130⁰, 50⁰

№2 - 6 , №3 - угол ВОС = 50⁰

2. Выполнить тест: у вас на партах лежат задания, связанные со свойствами четырехугольников. Подпишите свою фамилию.

З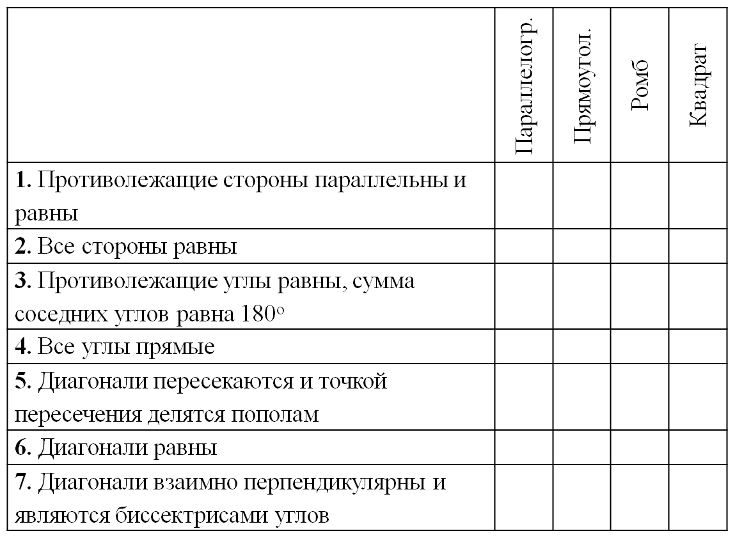аполните таблицу, отметив знаки «+» (да) и «- » (нет) в соответствующих клетках. На эту работу отводиться 3 минуты.

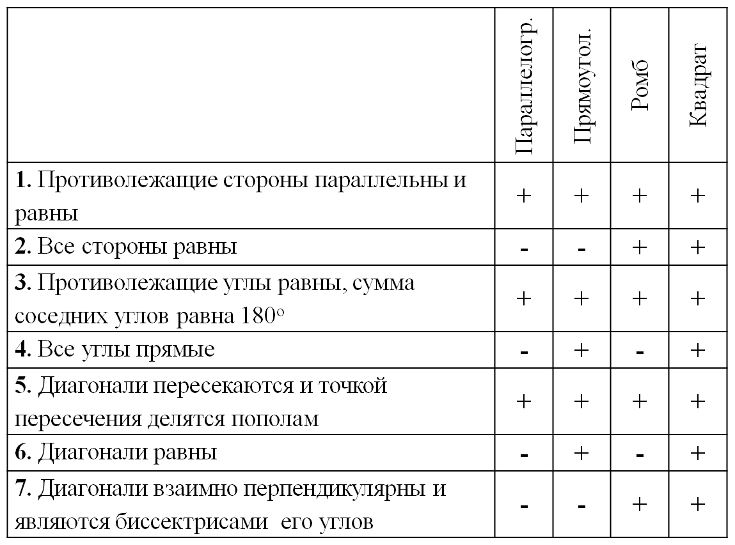
А теперь поменяйтесь работами и проверьте работу товарища, сверив ответ на слайде.

1-2 -«4»

3-5-«5»

Остальное 2

Вступительное слово учителя.

- учитель даёт задание, записанное на слайде

- объясняет как работать с тестом

- устно решают задачи;

работают по тесту, затем меняются работами и проверяют друг у друга

Регулятивные:

прогнозирование результата и оценивание уровня достижения результата.

Коммуникативные:

умение организовывать учебное сотрудничество и совместную деятельность с партнёрами,

умение участвовать в коллективном обсуждении проблемы, аргументировать свою позицию

Личностные:

умение управлять своей познавательной деятельностью

3.

Постановка темы и цели урока. (2 минут)

Задача: организовать познавательную деятельность учащихся.

Что вас привлекло на этих фотографиях?

Тема нашего осевая и центральная симметрия

- с помощью высказываний о симметрии и вопросов подводит учащихся к цели урока;

Личностное: смыслообразование.

Коммуникативные:

постановка вопросов.

Регулятивные:

целеполагание.

Познавательные:

умение делать вывод;

анализировать.

4.

Первичное усвоение новых знаний (18 мин)

Для этого мы сейчас выполним практическую работу.

Практическая работа №1

1) Возьмите лист белой бумаги, согните его пополам.

2) Проткните двойной лист ручкой, а затем разогните.

3) Вы получили две точки. Обозначьте одну буквой А, а другую - А₁.

4) Соедините А и А₁ отрезком и обозначьте точку пересечения отрезка АА₁ и линию сгиба точкой О

5) Измерьте расстояние от А и от А₁ до линии сгиба.

Расстояние от А до линии сгиба равно _______________________

Расстояние от А₁ до линии сгиба равно ______________________

6) Сравните эти расстояния. Они ____________________

7) Как называется точка пересечения отрезка и линии сгиба для отрезка АА₁ (точка О)

8) С помощью треугольника определите взаимное расположение отрезка АА₁ и линии сгиба

9) Определение:

Две точки А и А₁ называются симметричными относительно прямой, если эта прямая проходит через____________________ отрезка АА₁ и ______________________ к нему.

Вопросы к классу. Итак, какое определение у вас получилось.

Посмотрите на слайд. Проверим, а правы ли вы.

Определение 1: Две точки А и А₁ называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему.

Вопросы к классу

1. Как можно назвать прямую а?

2. Как построить точку симметричную данной относительно прямой? (сформулировать этапы)

Задание 1. На рисунке дан прямоугольник и прямая а, являющаяся осью симметрии. Внутри прямоугольника дана точка К. Постройте точку К₁, симметричную точке К относительно прямой а.

Вопросы к классу :Как мы будем строить? Каким инструментом воспользуемся?

Вопросы к классу

1. Если взять еще одну точку, принадлежащую прямоугольнику и построить ей симметричную, то будет ли она принадлежать прямоугольнику?

2. Как вы считаете, эта фигура симметрична относительно прямой а ?

Найдите в учебнике на стр111 определение фигуры симметрично относительно прямой.

Определение 2 Фигура называется симметричной относительно прямой, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

Задание 2. Вспомните изученные вами геометрические фигуры. (Ребята перечисляют известные им фигуры на плоскости) Попытайтесь провести ось симметрии в фигурах, которые вам достались (раздать листы с готовыми 2-3 геометрическими фигурами).

Вопросы к классу

1. Сколько осей симметрии у равнобедренного треугольника и равнобедренной трапеции?

2. Что вы можете сказать по поводу квадрата, прямоугольника, ромба?

3. Сколько осей симметрии у окружности?

4. Какой вывод отсюда следует? (Фигура может иметь как одну ось симметрии, так и несколько)

5. Какие фигуры не имеют оси симметрии?

Задание 3. Постройте отрезок АА₁ и найдите его середину точку О. Как иначе можно назвать точку О. (Центр). Найдите определение точки симметрично относительно центра симметрии..(уч. стр111)

Определение 3: Точки A и A₁ называются симметричными относительно точки О, если О - середина отрезка AA₁.

Вопросы к классу

1. Как построить точку симметричную данной относительно центра?( Попробуйте сформулировать алгоритм построение точек, симметричных относительно центра)

Практическая работа №2

Дано: параллелограмм АВСD.

Проведите диагонали параллелограмма.

Отметьте их точку пересечения О.

Отметьте на стороне АВ произвольную точку М и постройте точку М₁, симметричную точке М относительно центра О.

Отметьте на диагонали АС точку К, отличную от точки О и постройте точку К₁ симметричную точке К относительно центра О.

Сделайте вывод: если точка принадлежит параллелограмму, то где находится симметричная ей точка?

Вопросы к классу:

1. Какая фигура называется симметричной относительно центра?(учебник стр 111)

Определение 4. Фигура называется симметричной относительно центра, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

- даёт задания

- учащиеся выполняют практическую работу, делают выводы

Познавательные:

поиск нужной информации, умение анализировать условие, устанавливать причинно-следственные связи, выстраивать логическую цепочку;

Коммуникативные:

умение вести диалог, учитывать разные мнения в сотрудничестве

Личностные:

формирование способности к эмоциональному восприятию материала

Регулятивные:

способность к самооценке

.

Первичный контроль знаний (5 мин)

Задача: устранить пробелы в понимании материала.

Самостоятельная работа

Вариант №1

А

а

С

О

D

О - центр симметрии

Вариант №2

К

c

P

F

О

О - центр симметрии

Учащиеся выполняют задания на построение точек, симметричных относительно прямой и относительно точки. Каждый ученик получает задание.

Познавательные: самостоятельный выбор действия в соответствии с поставленной задачей;

Коммуникативные:

рефлексия своих действий

Личностные:

ответственное отношение к учению

Регулятивные:

действовать с учетом выделенных ориентиров

10.

Домашнее задание. (3 мин)

Задача:объяснить выполнения домашнего задания.

П47, в. 16-20, №418,421,423

доклад "Удивительный мир симметрии"(по желанию), презентацию

- учитель даёт задание;

- разъясняет выполнения домашего задания;

- отвечает на вопросы обучающихся.

- обучающиеся внимательно слушают;

- задают вопросы;

- делают записи в дневник.

Личностные: умение выделять нравственный апспект поведения, самоопределение.

Регулятивые: целеполагание и планирование учебного сотрудничества с учителем и сверстниками.

Познаватнльные:

умение ориентироваться в собственной системе знаний.

Коммуникативные:

умение слушать и воспринимать речь других.

Итог урока (3 мин)

Вопросы к классу

1. Какие виды симметрии вы можете назвать?

2. Где мы можем наблюдать симметрию?

3. Отрезок АВ, перпендикулярный прямой с, пересекает ее в точке О так, что АО=ОВ. Симметричны ли точки А и В относительно прямой с? (Ответ: да)

4. Прямая а пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а? (Ответ: нет)

5.Отрезок АС делится точкой М в отношении 2 к 3. Симметричны ли точки А и С относительно М?

.

.

Отвечают на вопросы.

.

Познавательные:

осознанное владение способами решения заданий;

Коммуникативные:

строить точное высказывание, аргументировать свою позицию

Регулятивные:

способность к самооценке

Самоанализ