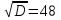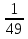Открытый урок на тему: «Решение показательных уравнений» (11 класс)

Открытый урок по математике по теме: «Решение показательных уравнений».

Цели:

• Образовательные:

  • актуализация опорных знаний при решении показательных уравнений;

  • обобщение знаний и способов решения; контроль и самоконтроль знаний;

  • поверка усвоения темы на обязательном уровне.

• Развивающие:

  • развитие умений в применении знаний в конкретной ситуации;

  • развитие умения сравнивать, обобщать, правильно формулировать и излагать мысли;

  • развитие навыков реализации теоретических знаний в практической деятельности;

  • развитие интереса к предмету через содержание учебного материала.

• Воспитательные:

  • воспитание навыков самоконтроля и взаимоконтроля;

  • воспитание культуры общения, умения работать в коллективе, взаимопомощи;

  • воспитание качеств характера таких как, настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.

Тип урока: урок повторения.

Форма работы - групповая, индивидуальная.

ХОД УРОКА

1.Организационный момент.

Приветствие учителя.

Проверка готовности студентов.

2. Проверка домашнего задания.

3. Постановка темы и сообщение целей урока.

Ребята, посмотрите на слайд. Скажите, какие уравнения Вы видите?

4^х=16, 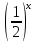=1, 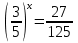, 8^х=1.

Ответ студентов: показательные уравнения.

Сформулируйте тему нашего урока?

Ответ студентов: Решение показательных уравнений.

Как Вы думаете, что сегодня на уроке мы будем повторять?

Ответ студентов: На уроке мы будем повторять основные способы решения показательных уравнений.

Какую цель мы поставим на уроке?

Ответ студентов: Закрепить знания, связанные с решением показательных уравнений.

4. Повторение теоретического материала.

А сейчас вспомним основные вопросы, связанные с решением показательных уравнений.

1. Какие уравнения называются показательными?

Определение. Показательным уравнением называется уравнение вида

a= b, где a > 0, a ≠ 1 и уравнения, сводящиеся к этому виду.

2. Сколько уравнений может иметь показательное уравнение?

Так как область значений функции у = a - множество положительных чисел, то при b < 0 и b = 0 - решений нет, при b > 0 - один корень.

3. Посмотрите на примеры и назовите методы решения уравнений:

а) 3= 1; б) 2= 16; в) 4 = -4; г)

(метод приведения к одинаковому основанию).

б) 5+1=0, 16^х+4^х*8+2=0

(метод приведения к квадратному уравнению).

3^х+1-3^х-2=26, 2+2= 20

(метод разложения на множители).

2= х+2, 4^х=5+х

(графический, метод подбора).

5. Тренировочные упражнения.

Работа учащихся в тетрадях и у доски.

1. Укажите промежуток, которому принадлежит корень уравнения и назовите метод решения показательного уравнения:

Метод приведения к одинаковому основанию.

25^3-х=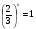

5^2(3-х)=5^-1

2(3-х)=-1

6-2х=-1

-2х=-7

х=3,5

1. (0;1) 2) (1;2) 3) (2;3) 4) (3;4)

Ответ:4

2. Найдите произведение корней уравнения и назовите метод решения показательного уравнения:

Метод приведения к одинаковому основанию.

3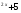=243

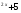3₌₃⁵

_х²_-1=5

_х²₌₆

_{х1= х2=-}

_{*(- )=-6}

_{Ответ: 1}

1) -6; 2)-4; 3) 4; 4) 6.

3. Решите уравнение, найдите сумму корней и назовите метод решения показательного уравнения:

Метод приведения к квадратному уравнению.

49 ∙ 7-50 ∙ +1=0

Введем замену: 7^х=t, где t

49t²-50t+1=0

D=50²-4*49*1=2500-196=2304;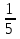

t₁=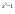

t₁=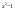

Вернемся к замене:

1. 7^х=1 2) 7^х=

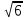
7^х=7⁰ 7^х=7^-2

х=0 х=-2

0+(-2)=-2

Ответ: 3

1) 1; 2) 2; 3) -2; 4) 50.

4. Найдите произведение корней и назовите метод решения показательного уравнения:

6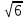=1

Метод приведения к одинаковому основанию.

6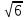=6⁰

х²-2х=0

х(х-2)=0

х=0 или х-2=0

х=2.

0*2=0

Ответ:2

1) -2; 2) 0; 3) 1; 4) 4.

На оценочном листе оцените свою работу в графе тренировочные упражнения (приложение 1).

Критерии оценивания.

2 балла - если задания выполнены безошибочно.

1 балл - если допущены1-2 ошибки.

1. баллов - если в задании допущены более 2 ошибок.

5. Работа в парах. (Взаимопроверка, сравнение решения по эталону на слайде).

Вариант 1 .

1. 3^х+2+3^х=30

3^х*3²+3^х=30

3^х(9+1)=30

3^х*10=30

3^х=3

х=1

Ответ: х=1

Вариант 1

2. 4^х-14*2^х-32=0

2^2х-14*2^х-32=0

Введем замену: 2^х=t,где t.

t²-14t-32=0

t₁=16 t₂=-2

Вернемся к замене:

1. 2^х=16 2) 2^х=-2

2^х=2⁴ решений нет

х=4

Ответ: 4.

Вариант 2.

1. 2^х+2+2^х=5

2^х*2²+2^х=5

2^х(2²+1)=5

2^х*5=5

2^х=1

2^х=2⁰

х=0

Ответ: х=0

Вариант 2

2. 9^х-6*3^х-27=0

3^2х-6*3^х-27=0

Введем замену:3^х= t,где t.

t²-6t-27=0

t₁=9 t₂=-3

Вернемся к замене:

1. 3^х =9 2) 3^х=-3

3^х =3² решений нет

х=2

Ответ:2.

На оценочном листе оцените свою работу в графе самостоятельная работа.

5. Индивидуальная работа с контролем на местах.

Решите показательные уравнения:

1. 7^х=

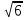
7^х=7^-3

х=-3

Ответ: х=-3.

2. ^х=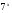

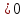
3^х=3^-2

х=-2

Ответ: х=-2.

=

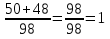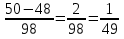
х=-2

Ответ: х=-2

4. 0,3^х*3^х=0,81

(0,3*3)^х=0,9²

0,9^х=0,9²

х=2

Ответ: х=2

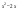⁰

3^2х+0,5=3⁰

2х+0,5=0

2х=-0,5

х=-0,25

Ответ: х=-0,25.

На оценочном листе оцените свою работу в графе индивидуальная работа.

5. Работа у доски.

Решите уравнения:

а)3*3^х*5^х=675

б)3^х*7^х+2=49*4^х

в)7^2х+1+7^2х+2+7^2х+3=57

г) 81^х - 8*9^х - 9 = 0

д) 9^х - 8*3^х--9=0

е)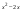

9. Самостоятельная тестовая работа.

Задания

Ответы

Вариант 1

Вариант 2

а

б

в

г

1)9^-1*3^х=81

1) 4^-1*2^х=8

6

2

5

1

2)2^х+2^х+2=20

2)3^х+2-3^х=24

-1

2

-2

1

3)2^2х+1-5*2^х+2=0

3)3^2х+1-10*3^х+3=0

1 и 1

0 и 1

0 и -1

2 и 3

На оценочном листе оцените свою работу в графе самостоятельная работа.

5. Подведение итогов урока.

Итак, что мы повторили сегодня на уроке?

Ответ студентов: Основные способы решения показательных уравнений.

Достигли ли мы поставленных целей? Возникли ли у Вас трудности при решении уравнений?

Ответ студентов.

5. Выставление оценок.

6. Домашнее задание.

Приложение.

Приложение 1

Лист оценивания.

Фамилия, имя

Актуализация знаний

Количество баллов

1. Тренировочные упражнения

2. Работа в парах

3. Индивидуальная работа

4. Работа у доски

5. Самостоятельная работа

Итого:

Оценка